Miks peab koolis õppima siinuseid ja neid teisi asju, kui neid elus vaja ei ole?
[Tuntud küsimus, mis kerkib tihti esile, kui kellelgi on vaja veel kord tõestada, kui elukauge ja kasutu on koolis õpetatav teadus. Ja kui valesti seda kõike tundides tehakse. Ja kuivõrd on õpetajad ning ainekavad ajast maha jäänud. Ja kui ainekeskene on meie kool, selle asemel, et olla õppijakeskne. Ja need teised asjad.]
Siinused ei ole tegelikult kasutud. Kolm näidet:
1. Maamõõtjad, arhitektid ja projekteerijad lasevad tänapäeval suurema osa arvutustest teha arvutitel ja ei pruugi tõesti teada, kuidas seal kolmnurksed või rombikujulised pinnad paika pannakse ja välja arvutatakse. Tarkvarainsener ja programmeerija, kes arvuti neid arvutusi tegema õpetab, peab seda ometi teadma ja siinuseid tundma. Peale selle on olemas üsna suur ja löögivalmis seltskond disainereid ning meistreid, kes näiteks teevad üksiktellimuste järgi mööblit ja õmblevad rõivaid. Nemad arvutavad kapiriiulite kuju ja konstrueerivad lõikeid ikka trigonomeetria ja Pythagorase teoreemi järgi. Kuidas siis teisiti?
2. Kui pikk on päev detsembri lõpus?
Pööripäeva paiku, kõige pimedamal ajal jääb neli päeva lühemaks kui 6 tundi ja 22 minutit. Vanarahvas ütles selle kohta, et Päike püsib kolm päeva pesas. Kas pole see mitte siinusfunktsiooni omadus, et maksimumi (ja tegelikult ka miinimumi) juures muutub ta väga aeglaselt, peaaegu seisabki paigal?
|
Kuupäev |
18.12. |
19.12. |
20.12. |
21.12. |
22.12. |
23.12. |
24.12. |
25.12. |
|
Päeva pikkus |
6:22:49 |
6:22:17 |
6:21:55 |
6:21:43 |
6:21:40 |
6:21:47 |
6:22:04 |
6:22:31 |
|
Muutus |
-40s |
-31s |
-22s |
-12s |
-3s |
+7s |
+16s |
+26s |
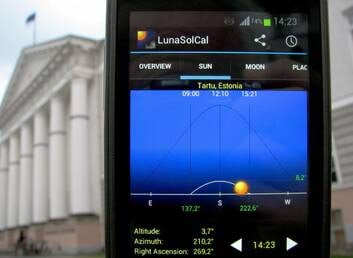
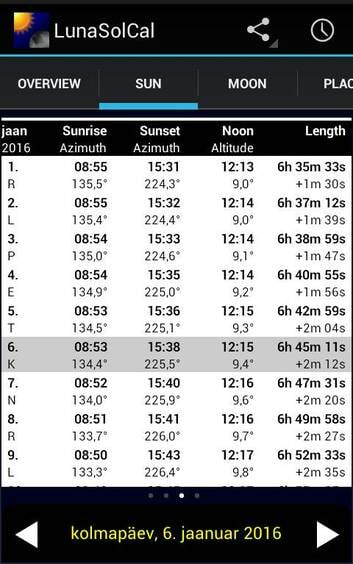
| Toomapäev Tartus. Päike on vaid 3,7 kraadi üle horisondi ja pilvine päev pole päris valgeks läinudki. Telefon näitab kalendris heleda joonega Päikese näiva teekonna madalat kaart. Tumeda joonega märgitakse suvise pööripäeva valgusolusid. See näeb ju päris sinusoidi moodi välja? | Programmi LunaSolCal ekraanivaade: tabel |
Kui lapsed jaanuari teisel nädalal jälle kooli lähevad, on päev juba umbes pool tundi pikem ja kogub pikkust üle kahe minuti iga pöördega. Rahvakalender lubab küll päeva pikenemist kukesammu võrra alles Tõnisepäevaks 17. jaanuaril. Kevadisel võrdpäevsusel, kui ka loodus pööraselt edasi tõttab, on päevane muutus 5 minutit. See püsib nii umbes kaks ja pool nädalat, siis hakkab tasapisi hoogu maha võtma.
3. Last but not least. Kes koolis koosinusvaba elu järgi õhkamise asemel trigonomeetria ära õpib, saab hiljem oma kooliealised lapsed kerge vaeva sellest samast teemast üle aidata. Valguse võit pimeduse üle!
Lisaküsimus
30° nurga siinus on ½ (pool). Millest pool? Miks pool?