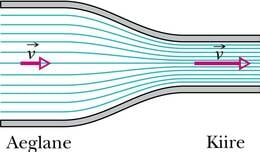
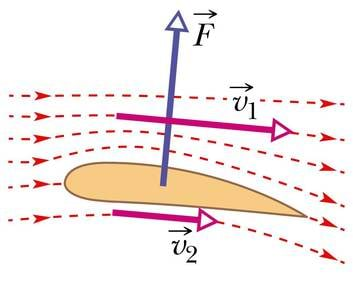
Üks huvitav ja mitmeid rakendusi leidnud nähtus, mida saab selgitada mehaanilise energia jäävuse seaduse kaudu, puudutab gaaside ja vedelike voolamist. Tutvume sellega lihtsustatud käsitluse kaudu.

Oletame, et ideaalne (so kokkusurumatu ja mitteviskoosne) vedelik voolab torus, mille läbimõõt pole kõikjal ühesugune. Siis toru erinevaid ristlõikepindu läbib sama ajaga alati sama ruumalaga vedelikukogus. On selge, et sellisel juhul peab voolukiirus toru peenemates osades olema suurem kui jämedamates.

Kui toru peenemas osas on vedeliku kiirus suurem, siis on seal suurem ka selle kineetiline energia. Hõõrdumise puudumisel on vedeliku mehaaniline energia jääv. Kui kineetiline energia suureneb, peab potentsiaalne samavõrra vähenema. Potentsiaalne energia on aga teatavasti tingitud süsteemi sees mõjuvatest jõududest. Antud juhul on tegemist vedeliku rõhumisjõududega. Näeme, et mida suurem on voolukiirus, seda väiksem on selles kohas vedeliku rõhk. Sama kehtib ka gaaside voolamisel.

Kirjeldatud seaduspärasuse avastas 1738. aastal šveitsi matemaatik ja füüsik Daniel Bernoulli. Tänapäeval tuntakse seda Bernoulli printsiibi nime all: voolava gaasi või vedeliku rõhk on suurem nendes piirkondades, kus kiirus on väiksem, ja väiksem seal, kus kiirus on suurem.

Bernoulli printsiipi kasutatakse mitmesuguste füüsikaliste nähtuste selgitamiseks. Näiteks võib öelda, et tormituul tõstab majalt katuse lendu sellepärast, et maja sees, kus õhk on paigal, on rõhk suurem kui katuse kohal tuule käes ja katus surutaksegi alt üles. Või siis pallimängudes, kus saab väita, et pöörlevana lendu löödud pall kaldub otsesihist kõrvale kuna õhu liikumise kiirus selle eri külgedel erinev ja tekib rõhkude vahe. Analoogiliselt seletatakse ka lennuki tiiva tõstejõudu —  tiiva asendi ja erilise kuju tõttu voolab õhk selle kohal kiiremini kui all, nii on tiiva all rõhk suurem ja see hoiabki lennukit õhus. Peab siiski ütlema, et kuigi nende nähtuste seletustes Bernoulli võrrandi alusel on tera tõtt, ei ole need paljudes põhiküsimustes täielikud. Sest Bernoulli printsiip kehtib vaid voolutorus, aga seda ei saa rakendada seeläbi, et me võrdleme üksteisest eraldatud vedelike (või gaaside) voolusid (nagu ühel ja teisel pool katust, palli või lennuki tiiba). Teiseks, Bernoulli printsiip kehtib vaid ideaalsete vedelike (ja gaaside) korral. Samas reaalsete vedelike liikumine on väga keerukas nähtus, mida ka tänapäeval täielikult ei mõisteta.

Daniel Bernoulli	Bernoulli printsiip leiab rakendust lennunduses