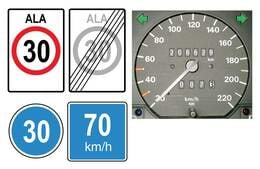
Kõik me oleme näinud sõidukite liikumiskiirust reguleerivaid teemärke ja teame, et politseinikud mõõdavad teedel sagedasti kiirust. Ohtlikematele teelõikudele on isegi automaatselt töötavaid kiiruskaameraid üles seatud. Autojuhtidel aitab kiiruspiiranguid järgida armatuurlaual paiknev spidomeeter (speed [spi:d] — inglise k kiirus) ja sarnase kiirusemõõtja saab monteerida isegi jalgrattale.
Mis liiki kiirusega siin tegemist on? Vaevalt, et keskmisega, sest kuidas saaks liiklusmärgi ülespanija või politseinik arvestada sõidukijuhi juba asetleidnud ja veel vähem alles eel olevaid kihutamisi ja seisakuid! Pealegi ei oma juba toimunud ja tulevane liikumine konkreetse hetke liiklusolukorras mingit tähtsust. Oluline on ju see, kuidas liigutakse selles paigas just sellel ajahetkel. Siin kirjeldatud juhtudel kasutatav kiirus on hetkkiirus.
Hetkkiiruse nimetus viitab sellele, et mõeldud on kiirust mingil konkreetsel ajahetkel. Samas on hetke kestus null ja selle kestel läbitav teepikkus samuti null. Püüdes nüüd kiirust arvutada, jõuame välja võimatu tehteni, mida matemaatikud tunnevad kui 0/0 määramatust. Mis ikkagi hetkkiirus on ja kuidas seda mõõdetakse?
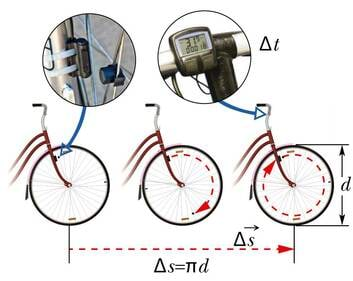
Jalgratta kiirusemõõtja kujutab endast pisikest kellaga arvutit, mille külge on ühendatud väike magnetvälja muutusi tajuv andur. Andur paikneb esiratta kõrval nii, et kodara külge kinnitatud magnet ratta iga täisringi järel andurile oma möödumisest teada annab. Arvuti kell mõõdab ratta täisringi tegemiseks kulunud aja ja lähtudes mälusse sisestatud ratta läbimõõdu väärtusest, leiab ühe rattaringi jooksul sooritatud nihke pikkuse ning arvutab välja selle lühikese teejupikese läbimise keskmise kiiruse.
|
|
|---|---|
| Jalgratta kiirusemõõtja tööpõhimõte | Kõverjoonelise liikumise hetkkiiruse leidmine. Ka siin peab t olema võimalikult väike |
Hetkkiiruse all mõistetakse küll keha liikumiskiirust kindlal ajahetkel, aga selle väärtust saab hinnata siiski mitte hetke, vaid lühikese ajavahemiku kestel leitava keskmise kiirusena.
Hetkkiiruse tähistamiseks kasutatakse sarnaselt ühtlase liikumise kiirusega sümbolit v. Kui võtame lühikese ajavahemiku, mille kestel kiirus ei jõua oluliselt muutuda, tähiseks Δt ja selle aja jooksul sooritatud nihke pikkuse tähiseks Δs, saame hetkkiiruse arvutusvalemiks
Mida lühem on uuritav ajavahemik Δt, seda täpsemini saab hetkkiiruse teada, sest seda vähem jõuab kiirus selle ajaga muutuda. Mitteühtlase liikumise hetkkiirus on sarnaselt ühtlase liikumise kiirusega vektoriaalne ehk suunaga suurus. Kui liikumise kirjeldamisel on ka suund oluline, tuleb hetkkiiruse valemit kasutada vektorkujul.