1906. aastal asutati Eesti Noorsoo Kasvatuse Seltsi I järgu Tütarlaste Kool, mida tänapäeval, mitmete nimemuutuste järel, tunneme Miina Härma Gümnaasiumina. Õppekeeleks sai eesti keel, eksamid tuli siiski õiendada vene keeles. Sel ajal ei olnud Eesti- ja Liivimaal (ega ka Venemaal, Euroopas ja terves Maailmas) kuigi palju neid, kes oleksid uskunud, et eesti keeles on võimalik gümnaasiumi tasemel õpetada, teadusest rääkida ja kirjutada. Üks, kes sellesse uskus, oli füüsika ja matemaatika õpetaja Jaan Sarv. Töötades 1909. aastast tütarlastekooli õpetajana, korraldas ta lahtisi tunde, näitamaks, et eesti keel on täiesti kõlblik loodusteadustest rääkimiseks. Ühele klassile andis ta avaliku tunni Vanemuises, et kõik skeptikud saaksid kuulama tulla ja veenduda, matemaatika õpetamisel ei tule sõnadest puudu. Tunni teemaks olevat olnud – viltu väli. Samal ajal kirjutas ta kaks füüsika õpikut – Füüsika õpetus ja Elekter. 1918. aastal kutsus tuntud haridustegelane Peeter Põld oma sõbra ja mõttekaaslase Jaan Sarve Eesti ülikooli rajamise tööle. Probleem, täpsemalt üks probleemidest, oli sama, mis gümnaasiumi asutamisel. Paljud saksa ja vene keeles õpetavad professorid ei uskunud, et eesti keelest võib saada teaduskeel.
„Füüsika õpetus” on üle 100 aasta vana, terminoloogia ja keelekasutus on aja jooksul veidi muutunud, aga teemade käsitlus on üllatavalt kaasaegne. Muu hulgas esitab autor näidisküsimusi, tänapäevases kõnepruugis püstitab probleeme, millega varemõpitut seostab ja kokku võtab. Ka klassikaline hõõrdevaba kaldpinna ülesanne leiab siin kasutamist vektori komponentideks jagamise seletamisel.
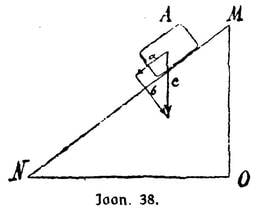
Olgu üks keha A pärissiledal viltupinnal MN (joon. 38). Olgu see pind maa peal seisva päriskindla keha pind. Kuidas mõjub raskuse tung selle keha peale?
Jaan Sarv, Füsika õpetus – Tallinnas, 1910. Näidisülesanne peatükist „Raskus”.
PDF: http://www.digar.ee/arhiiv/nlib-digar:101608
Tähendame noole c-qa seda otse allapoole sihitud liikumise hulka, mida raskuse tung igal sekundil kehale A anda püüab. Lahutame selle liikumise hulga mõttes kaheks, nii et üks pinnale MN parallelne ja teine temale perpendikularne on. Siis tähendab nool a parallelset ja nool b perpendikularset liikumise hulka. Liikumise hulk b ei saa ilmuda, sest pind MN takistab teda. Liikumise hulk a ilmub igal sekundil ja jääb täielikult kehale A, sest pärissiledal pinnal ei ole hõõrumist. Keha A saab siis igal sekundil ühepalju kiirust juurde, nagu vabalt langev keha. Aga see juurdetulev kiirus on 9,81 m/s-st nii mitu korda vähem, kui mitu korda nool a noolest с lühem on. Kui siht МО vertikalne on ja siht NO temaga õige nurga sünnitab, siis nimetatakse kaugust MO viltupinna kõrguseks, kaugust NO tema aluseks ja kaugust MN tema pikkuseks. Joonistuselt selgub, et kolmnurk MNO nooltekolmnurgaga sarnane on.
Selle põhjal võib lühendatult ütelda: raskuse kiirestus viltupinnal on nii mitu korda vähem raskuse kiirestusest vabas ruumis,kui mitu korda viltupinna kõrgus tema pikkusest vähem on. Olgu näituseks MО=30 m ja MN= 60 m. Olgu sellele viltupinnale üks keha pandud, ilma et teda kudagi oleks lükatud. See keha hakkab pinda mööda alla libisema ja saab igal sekundil 9,81/3 m/s ehk ligi 5 m/s kiirust juurde. Kolme sekundi päralt on siis selle keha kiirus 3·5=15 m/s.
Libisemist viltupinnal näeme jõgedes, kus vesi jõe põhja mööda libiseb või vee ülemised kihid alumiste kihtide üle libisevad. Hariliku langemise ja libisemise kohta ei ole kõik rehkenduse otsused mitte täieste õiged, sest harilikult takistab õhk visatud kivi või suurtüki kuuli liikumist ja iga hariliku pinna peal kaotavad libisevad kehad hõõrumise mõjul oma liikumist. Aga mida vähem õhu takistus ja mida siledam libisemise pind on, seda vähem läheb harilik kehade liikumine väljarehkendatud liikumisest lahku.