Üks füüsika ammuseid eesmärke on olnud mõista gravitatsioonijõudu – jõudu, mis hoiab meid maakera pinnal, hoiab Kuud tiirlemas orbiidil ümber Maa ja hoiab Maad tiirlemas orbiidil ümber Päikese. See jõud valitseb kaugemalgi – Linnutee galaktikas hoiab ta liikumas miljardeid tähti ning loendamatut hulka molekule ja tolmuosakesi tähtedevahelises ruumis. Me asume selle kettakujulise tähekogumi äärealal, umbes 2,6×104 valgusaasta (2,5×1020m) kaugusel Galaktika keskpunktist, mille ümber me aeglaselt tiirleme.
Gravitatsioonijõud ulatub ka läbi galaktikatevahelise ruumi, hoides koos kohalikku galaktikaparve (nn Kohalikku Gruppi), millesse kuuluvad peale Linnutee veel ka Andromeeda galaktika (joonis 13-1), mis asub 2,3×106 valgusaasta kaugusel Maast, ja mitmed lähemad kääbusgalaktikad nagu Suur Magalhãesi Pilv. Kohalik Grupp on osa Kohalikust Superparvest, mida gravitatsiooniliselt tõmbab erakordselt massiivne, Suureks Atraktoriks nimetatud ruumipiirkond. See piirkond paistab olevat Linnutee vastaspoolel umbes 3,0×108 valgusaasta kaugusel Maast. Kuid gravitatsioonijõud ulatub veelgi kaugemale, hoides koos kogu paisuvat Universumit.
Gravitatsioonijõududega on seotud ka ühed väga salapärased struktuurid Universumis, nimelt mustad augud. Kui Päikesest märgatavalt massiivsem täht põletab lõpuni ära oma tuumakütuse varu, siis võib kõikide tema osakeste vahel mõjuv gravitatsioonijõud viia selleni, et täht variseb täielikult kokku (kollabeerub) ja moodustab seeläbi musta augu. Gravitatsioonijõud on kollabeerunud tähe pinnal niivõrd tugevad, et ei osakesed ega isegi valgus ei suuda lahkuda tähe pinnalt (sellest siis ka nimetus „must auk”). Mustale augule liiga lähedale sattunud tähte ähvardab lõhkikiskumine gravitatsioonijõudude poolt ja tema jäänuste langemine musta auku. Piisav hulk sellist saaki viib ülimassiivse musta augu moodustumiseni. Taolised salapärased koletised paistavad olevat Universumis üsna tavalised.
Hoolimata sellest, et gravitatsioonijõu olemus ei ole seni veel lõpuni selge, on lähtekohaks selle jõu mõistmisel Isaac Newtoni formuleeritud gravitatsiooniseadus.
Füüsikutele meeldib uurida pealtnäha seosetuid nähtusi ja näidata, et nende vahel on võimalik leida seos, kui vaid uurida piisava põhjalikkusega. Selliste ühendteooriate otsimine on kestnud nüüdseks juba sajandeid. Aastal 1665 andis 23-aastane Isaac Newton olulise panuse füüsika arengusse, kui näitas, et jõud, mis hoiab Kuud tema orbiidil, on seesama jõud, mille tõttu õun kukub maapinnale. Tänapäeval peame me seda teadmist nii enesestmõistetavaks, et meil ei ole lihtne aru saada muistsest usust, et maiste ja taevaste kehade liikumised on erinevat liiki ja et neid valitsevad ka erinevad seadused.
Newton järeldas, et mitte ainult Maa ei tõmba nii õuna kui ka Kuud enda poole, vaid et iga keha Universumis tõmbab iga teist keha enda poole. Seda kehade omadust tõmbuda üksteise poole nimetatakse gravitatsiooniks. Newtoni järeldusega harjumine võtab natuke aega, sest maiste kehade puhul ületab harjumuspärane Maa külgetõmme oluliselt kehade omavahelist külgetõmmet. Näiteks tõmbab Maa õuna jõuga, mille tugevus on umbes . Inimene tõmbab lähedalasuvat õuna (ja see õun tõmbab inimest), aga selle tõmbejõu tugevus on väiksem kui tolmukübemekese kaal.
Newton esitas jõu arvutamise seaduse, mida me tunneme Newtoni gravitatsiooniseadusena: iga osake (punktmass) tõmbab iga teist osakest (punktmassi) gravitatsioonijõuga, mille tugevus on
Siin on ja osakeste massid, nendevaheline kaugus ja on gravitatsioonikonstant, mille väärtus praeguste teadmiste kohaselt on
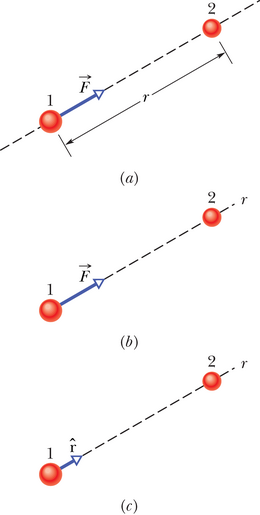
Joonisel 13-2a on kujutatud gravitatsioonijõud , millega osake 2 (massiga ) mõjub osakesele 1 (massiga ). See jõud on suunatud osakese 2 poole ja ta on tõmbejõud, sest osakest 1 tõmmatakse osakese 2 poole. Jõu tugevus on antud valemiga 13-1.
Me võime jõu esitada vektorina, mis on suunatud osakesest 1 kuni osakeseni 2 ulatuva r-telje positiivses suunas (joonis 13-2b). Samuti võime jõu esitamiseks kasutada radiaalset ühikvektorit TeX parse error: Missing argument for \mathrm (dimensioonitut ühikulise pikkusega vektorit), mis on suunatud osakesest 1 eemale mööda r-telge (joon 13-2c). Kasutades valemit 13-1 on osakesele 1 mõjuv jõud nüüd esitatav kujul
Osakesele 2 mõjuv gravitatsioonijõud, mille tekitab osake 1, on niisama tugev kui osakesele 1 mõjuv jõud, aga ta on vastassuunaline. Need kaks jõudu moodustavad Newtoni kolmanda seaduse jõupaari ja me saame rääkida gravitatsioonijõust, mis mõjub kahe osakese vahel valemist 13-1 arvutatud tugevusega. See kahe osakese vahel mõjuv jõud ei muutu teiste kehade olemasolul isegi siis mitte, kui need kehad asuvad kahe osakese vahel. Ehk teisiti öeldes, ükski keha ei saa varjestada osakest teise osakese tekitatud gravitatsioonijõu eest.
Gravitatsioonijõu tugevus – see, kui tugevalt teineteisest teataval kaugusel asuvad teatavate massidega osakesed teineteist tõmbavad – sõltub gravitatsioonikonstandi väärtusest. Kui gravitatsioonikonstandi väärtus äkki imekombel suureneks 10 korda, siis oleks Maa gravitatsioonijõud nii tugev, et Maa külgetõmme suruks inimesed vastu põrandat lapikuks. Kui aga gravitatsioonikonstandi väärtus väheneks sama arv korda, siis oleks Maa külgetõmme nii nõrk, et inimene suudaks hüpata üle hoonete.
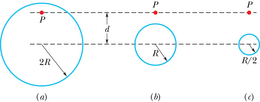
Rangelt võttes kehtib Newtoni gravitatsiooniseadus üksnes punktisarnaste objektide jaoks, aga me saame seda kasutada ka reaalsete kehade korral, kui nende mõõtmed on väikesed, võrreldes kaugusega kehade vahel. Näiteks Maa ja Kuu on teineteisest piisavalt kaugel, et neid heas lähenduses käsitleda punktosakestena. Aga kuidas on olukord Maa ja õuna korral? Õuna seisukohast vaadatuna ei ole tema all silmapiirini tasaselt laiuv maapind küll vähimalgi määral punktosakese sarnane.
Newton lahendas õuna–Maa probleemi sellega, et tõestas olulise teoreemi, mida tuntakse kihiteoreemina:
Ühtlane sfääriline ainekiht (kerakiht) tõmbab väljaspool kihti asuvat punktosakest enda poole nii, nagu oleks kihi kogu mass koondunud sfääri (kera) keskpunkti.
Me võime kujutleda Maad selliste üksteise sees asuvate kerakihtide kogumina, kusjuures iga kiht tõmbab Maa pinna kohal asuvat punktosakest nii, nagu oleks kihi kogu mass koondunud kihi keskpunkti. Seega, õuna vaatepunktist käitub Maa ikkagi nagu punktmass, mis asub Maa keskpunktis ja mille mass võrdub Maa massiga.
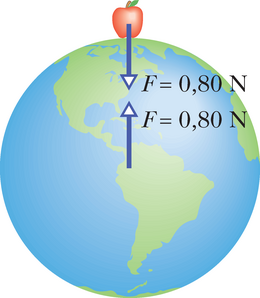
Oletame, et Maa tõmbab õuna enda poole jõuga, mille tugevus on , nagu on kujutatud joonisel 13-3. Seega peab ka õun tõmbama Maad enda poole jõuga, mille tugevus on , kusjuures see jõud on rakendatud Maa keskpunkti. Hoolimata sellest, et nii õunale kui ka Maale mõjub võrdse tugevusega jõud, on nende kiirendused pärast õuna lahtilaskmist erinevad. Õuna kiirendus on umbes , mis on harilik vaba langemise kiirendus maapinna lähedal. Seevastu Maa kiirendus, mõõdetuna süsteemi õun–Maa massikeskmega seotud taustsüsteemis, on vaid umbes .
KONTROLLKÜSIMUS 1
Punktosakeste süsteemi poolt tekitatud gravitatsioonilise resultantjõu leidmiseks, mis mõjub ühele neist punktosakestest, kasutame superpositsiooniprintsiipi. See on üldine printsiip, mis väidab, et kogumõju on üksikute mõjude summa. Siin tähendab see seda, et kõigepealt peame arvutama üksikute süsteemi kuuluvate punktosakeste tekitatud gravitatsioonijõud, mis mõjuvad meie poolt välja valitud punktosakesele, ja seejärel leiame resultantjõu kui kõigi nende jõudude vektorsumma.
Vastavalt superpositsiooniprintsiibile saame osakesest koosneva süsteemi korral kirjutada osakesele 1 mõjuva gravitatsioonijõu avaldise kujul
Siin on osakesele 1 mõjuv resultantjõud ja näiteks on jõud, millega osake mõjub osakesele . Selle seose saame esitada kompaktsemalt vektorsummana:
Kuidas aga arvutada gravitatsioonijõudu, millega reaalne (ruumiline) keha mõjub punktosakesele? Selle jõu saame leida, kui jagame keha piisavalt väikesteks osadeks nii, et saame neid osasid samuti vaadelda punktosakestena, ning seejärel kasutame valemit 13-5, leidmaks punktosakesele mõjuvate jõudude vektorsumma. Piirjuhul saame keha jagada lõpmata väikesteks osadeks massiga , millest igaüks mõjub uuritavale punktosakesele lõpmata väikese jõuga . Sellisel juhul saame valemis 13-5 esineva summa asendada integraaliga
kusjuures integraal arvutatakse üle kogu ruumilise keha ja võime alaindeksi „res” ära jätta. Juhul kui ruumiline keha on kas ühtlane kera või kerakiht (seest tühi kera), siis pole valemi 13-6 integraali tarvis arvutada, sest võime eeldada, et ruumilise keha mass on koondatud tema keskmesse, ja kasutada valemit 13-1.
KONTROLLKÜSIMUS 2
Näidisülesanne 13-1
Lahendus
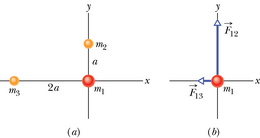
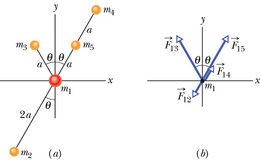
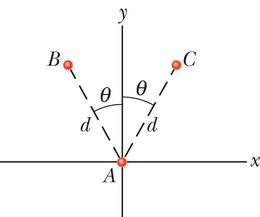
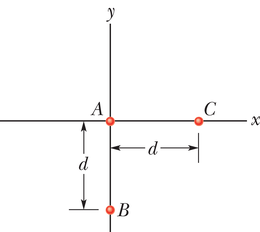
JUHTMÕTTED (1) Kuna meil on tegemist punktosakestega, siis saab osakesele mõjuva jõu tugevuse arvutada valemist 13-1 (F=Gm1m2/r2). (2) Osakesele mõjuv gravitatsioonijõud on suunatud seda jõudu tekitava osakese suunas. (3) Kuna mõjuvad jõud ei ole suunatud piki sama telge, siis me ei saa lihtsalt liita ega lahutada nende arvulisi väärtusi või nende komponente, selleks et leida resultantjõudu. Me peame jõuvektorid liitma vektorsummaks.
Arvutused: Kasutades valemit 13-1, saame arvutada osakesele mõjuva jõu tugevuse , mille tekitab osake :
Sarnaselt saame arvutada osakesele mõjuva jõu tugevuse , mille tekitab osake :
Jõud on suunatud -telje positiivses suunas (joonis 13-4b) ja sellel jõul on seega ainult y-komponent suurusega F12. Analoogiliselt saame, et on suunatud -telje negatiivses suunas ja tal on ainult -komponent suurusega −F13.
Et leida osakesele mõjuvat resultantjõudu →F1,res, peame need kaks jõuvektorit liitma vektorsummaks. Seda võime teha vastavat funktsiooni omaval kalkulaatoril. Siiski, paneme tähele, et −F13 ja F12 on tegelikult vektori →F1,res - ja -telje suunalised komponendid. Seega saame kasutada valemit 3-6, et leida kõigepealt jõu F1,res suurus ning seejärel ka suund. Jõu suurus on
Valemi 3-6 abil saame arvutada ka →F1,res nurga -telje positiivse suuna suhtes:
Kas see on mõistlik tulemus? Ei ole, sest vektori →F1,res suund peab olema vektorite ja poolt määratud suundade vahel. Meenutame 3. peatükist (ülesannete lahendamise juhised, juhis 3), et kalkulaator annab vastusena ainult ühe võimaliku tan−1 väärtuse kahest. Teise võimaliku väärtuse leiame, kui liidame :
mis on vektori →F1,res jaoks mõistlik suund.
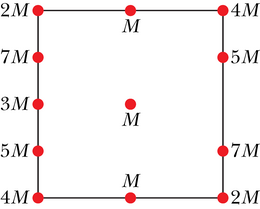
Näidisülesanne 13-2 Arenda oma oskusi
Lahendus
JUHTMÕTTED (1) Kuna meil on tegemist punktosakestega, siis on osakesele mõjuva jõu suurus arvutatav valemiga 13-1 (F=Gm1m2/r2). (2) Osakesele mõjuv gravitatsioonijõud on suunatud seda jõudu tekitava osakese poole. (3) Me võime kasutada süsteemi sümmeetriat selleks, et arvutusi lihtsustada.
Arvutused: Arvutades osakesele mõjuvate jõudude tugevusi, paneme esmalt tähele, et osakesed ja on võrdse massiga ja asuvad osakesest võrdsetel kaugustel r=2a. Valemist 13-1 leiame
Kuna osakesed ja on võrdse massiga ja asuvad mõlemad osakesest kaugusel r=a, leiame analoogiliselt, et
Me võime neisse kahte valemisse asetada teadaolevad arvulised väärtused ja arvutada vastavate jõudude tugevused. Seejärel võime kujutada jõudude suunad osakesele mõjuvate jõudude vektordiagrammil, nagu on tehtud joonisel 13-5b, ja siis leida resultantjõu, mida saab teha kahel viisil: (1) jagades vektorid - ja -komponentideks, leides vastavalt resultantjõu - ja -komponendid ning ühendades need vastavalt vektoralgebra reeglitele või (2) liites vektorid vastavat funktsiooni omaval kalkulaatoril.
Selle kõige asemel aga võime veel kasutada ülesande sümmeetriat. Esmalt paneme tähele, et vektorid ja on võrdsete pikkuste ja vastupidiste suundadega ning seega nad kompenseerivad teineteist. Arvestades valemit 13-8, paneme joonist 13-5b kasutades tähele, et ka jõudude ja F15 -telje sihilised komponendid kompenseerivad teineteist. Nende jõudude -komponendid on võrdsete pikkustega ning mõlemad on suunatud -telje positiivses suunas. Seega resultantjõud →F1,res mõjub -telje positiivses suunas ja tema suurus on kaks korda suurem vektori y-komponendi väärtusest:
Paneme tähele, et osake , mis asub osakeste ja vahel, ei muuda gravitatsioonijõudu, millega osake mõjub osakesele .
Juhis 1: Gravitatsioonijõu vektorite kandmine joonisele
Gravitatsioonijõu vektorite kandmine joonisele.Olgu antud punktosakeste asetus, nagu näiteks joonisel 13-4a, ja palutud leida gravitatsiooniline resultantjõud, mis mõjub ühele kindlale osakesele. Kõigepealt tuleb joonistada osakesele mõjuvate jõudude vektordiagramm, kuhu on kantud üksnes huvipakkuv osake ning seejärel ka üksnes sellele osakesele mõjuvad jõud, nagu on tehtud joonisel 13-4b. Kui te aga eelistate joonistada jõuvektorid osakeste asendit kujutavale joonisele, tuleb hoolega vaadata, et kõigi jõuvektorite alguspunktid (soovitatavalt) või tipud oleksid sellel osakesel, millele need jõud mõjuvad. Kui te joonistate vektorid mujale, tekitate asjata segadust, ja segadus on garanteeritud, kui te joonistate vektorid jõudu põhjustavatele osakestele.
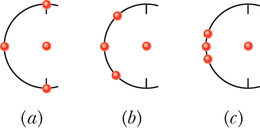
Juhis 2: Sümmeetriliste jõudude liitmise lihtsustamine
Näidisülesandes 13-2 kasutasime ülesandes olevat sümmeetriat. Nähes, et osakesed ja asetsevad sümmeetriliselt osakese 1 suhtes, saime järeldada, et jõud ja kompenseerivad teineteist. Seega ei olnud meil vaja kumbagi jõudu eraldi arvutada. Pannes järgnevalt tähele, et jõudude ja -telje sihilised komponendid kompenseerivad teineteist ning et nende jõudude -komponendid on võrdsed ja liituvad algebraliselt, saime vajalikke arvutusi veelgi vähendada.
Sümmeetriat sisaldavate ülesannete lahendamine lihtsustub sageli oluliselt, sest sümmeetria võimaldab osa arvutusi tegemata jätta ning seetõttu väheneb ka arvutusvea tegemise võimalus. Ülesandes leiduva sümmeetria tabamise oskus areneb ülesannete lahendamise käigus.
Eeldame, et Maa on ühtlane kera massiga . Kui punktosake massiga m asub Maa pinna kohal kaugusel Maa keskpunktist, siis on temale mõjuva Maa gravitatsioonijõu tugevus vastavalt valemile 13-1
Kui osake lahti lasta, siis hakkab ta gravitatsioonijõu mõjul langema Maa keskpunkti suunas kiirendusega, mida nimetatakse gravitatsioonikiirenduseks ehk raskuskiirenduseks . Newtoni teise seaduse kohaselt on suurused ja omavahel seotud,
Asendades suuruse valemist 13-9 valemisse 13-10 ja lahendades selle suhtes, saame
Tabelis 13-1 on toodud ag väärtused, mis on arvutatud eri kõrgustel Maa pinnast. Paneme tähele, et on märkimisväärne isegi kõrgusel.
| Kõrgus (km) | () | Kõrguse näide |
| Maapinna keskmine kõrgus | ||
| Džomolungma | ||
| Kõrgeim mehitatud õhupall | ||
| Kosmosesüstiku orbiit | ||
| Sidesatelliit |
Alates punktist 5-4 oleme eeldanud, et Maa on inertsiaalsüsteem ja pole arvestanud Maa pöörlemist. See lihtsustus lubas meil eeldada, et osakese vaba langemise kiirendus on identne osakese raskuskiirendusega, mida me tähistame . Veelgi enam, me eeldasime, et on ühesuguse väärtusega Maa pinna igas punktis. Tegelikult erineb konkreetses asukohas mõõdetud väärtus sama asukoha jaoks valemist 13-11 arvutatud ag väärtusest. See erinevus tuleneb kolmest asjaolust: (1) Maa mass ei ole jaotunud ühtlaselt, (2) Maa ei ole ideaalne kera ja (3) Maa pöörleb. Veelgi enam, kuna erineb ‑st, siis neil kolmel loetletud põhjusel erineb ka osakese mõõdetud kaal osakesele mõjuva gravitatsioonijõu tugevusest, mis on antud valemiga 13-9. Järgnevalt vaatame neid põhjuseid lähemalt.
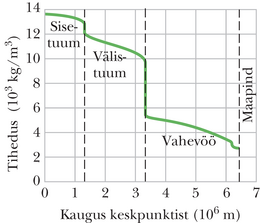
- Maa mass ei ole jaotunud ühtlaselt. Maa tihedus (mass ruumalaühiku kohta) muutub radiaalsuunaliselt (joonis 13-6) ja lisaks on maakoore (Maa välimise osa) tihedus piirkonniti erinev. Seega muutub väärtus piirkonniti, sõltuvalt asukohast Maakera pinnal.
- Maa ei ole ideaalne kera. Maa on ligikaudu ellipsoid, mis on poolustelt kokku surutud ja ekvaatori kohal välja venitatud. Maa ekvatoriaalne raadius on suurem kui polaarraadius. Seega on poolusel asuv punkt Maa tihedale tuumale lähemal kui ekvaatoril asuv punkt. See on üks põhjustest, miks vaba langemise kiirendus suureneb, kui liikuda merepinna tasemel ekvaatorilt ükskõik kumma pooluse poole.
- Maa pöörleb. Maa pöörlemistelg läbib Maa põhja- ja lõunapoolust. Maa pinnal asuv keha, kui ta ei ole täpselt poolusel, liigub mööda ringjoont ümber pöörlemistelje ja seega on sel kehal ka tsentripetaalkiirendus, mis on suunatud ringjoone keskpunkti poole. Sellele tsentripetaalkiirendusele vastab tsentripetaaljõud, mis on samuti suunatud ringjoone keskpunkti poole.
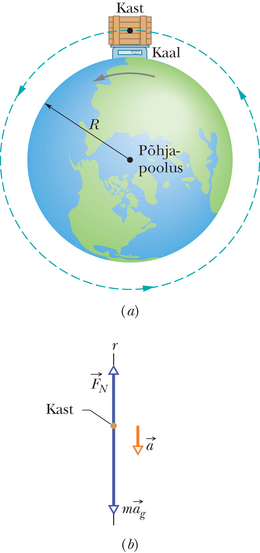
Selleks et mõista, kuidas Maa pöörlemine põhjustab ja erinevuse, vaatame lihtsat näidet. Paiknegu kast massiga m kaalul, mis asub ekvaatoril. Joonisel 13‑7a on kujutatud seda olukorda nii, nagu see paistaks vaadatuna kosmosest põhjapooluse kohalt.
Kastile mõjuvate jõudude vektordiagramm on kujutatud joonisel 13-7b. Jooniselt on näha, et kastile mõjub kaks jõudu, mis on suunatud mööda radiaalsuunalist r-telge alguspunktiga Maa keskpunktis. Kastile mõjuv kaalu normaaljõud on suunatud r-telje positiivses suunas (väljapoole). Gravitatsioonijõud, esitatuna kujul , on suunatud Maa keskpunkti poole. Et Maa pööreldes liigub kast ligikaudu mööda ringjoont, siis on kastil ka tsentripetaalkiirendus , mis on suunatud Maa keskpunkti suunas. Valemist 10-23 () teame, et tsentripetaalkiirendus on arvutatav kui , kus on Maa nurkkiirus ja on selle ringjoone raadius, mida mööda liikumine toimub (käesoleval juhul ligikaudu Maa raadius). Nüüd saame kirjutada Newtoni teise seaduse r-telje sihiliste jõukomponentide jaoks () kujul
Normaaljõu tugevus on võrdne kasti mõõdetud kaaluga . Asendades valemis 13-12 normaaljõu suurusega saame
mis ütleb meile, et
Seega on kasti mõõdetud kaal väiksem kui kastile mõjuv gravitatsioonijõud, sest nüüd oleme arvestanud ka Maa pöörlemisega. Jagades valemi 13-13 läbi massiga m saame seose ja vahel,
mis ütleb meile, et
Seega on Maa pöörlemise tõttu vaba langemise kiirendus väiksem kui raskuskiirendus.
Vaba langemise kiirenduse ja raskuskiirenduse vahe on võrdne suurusega ning see vahe on suurim ekvaatoril (üheks põhjuseks see, et ringjoone raadius, mida mööda kast liigub, on suurim ekvaatoril). Selle vahe leidmiseks saame kasutada valemit 10-5 () ja Maa raadiuse arvulist väärtust . Ühele täispöördele vastav nurk on võrdne radiaaniga ja üheks täispöördeks kuluv ajavahemik on ligikaudu 24 tundi. Kasutades suuruste teadaolevaid väärtusi (ja teisendades tunnid sekunditeks) leiame, et vaba langemise kiirendus on raskuskiirendusest ag väiksem suuruse võrra, mis on väike võrreldes tema väärtusega . Seetõttu on ja erinevuse mittearvestamine enamasti põhjendatud. Samuti on põhjendatud ka kaalu ja raskusjõu erinevuse mittearvestamine.
Näidisülesanne 13-3
Lahendus
JUHTMÕTTED Maad vaatleme ühtlase kerana, mille mass on MMaa. Sel juhul on raskuskiirendus Maa keskpunktist kaugusel leitav valemist 13-11
Seda valemit võime kasutada nii jalgade r=6,77×106m kui ka pea r=6,77×106m+1,70m jaoks. Kuna aga astronaudi pikkus on väga väike võrreldes kaugusega , siis võime kalkulaatorit kasutades saada suuruse jaoks ühe ja sama arvu ning ülesande vastus (kalkulaatori täpsusega) oleks . Kuna astronaudi pea ja jalgade kaugused Maa keskpunktist võime lugeda erinevaks vaid diferentsiaali dr võrra, siis võime täpsema vastuse leidmiseks valemit 13-15 diferentseerida muutuja järgi.
Arvutused: Diferentseerides valemit 13-15 saame
kus dag on raskuskiirenduse diferentsiaal, mis vastab kauguse diferentsiaalsele muudule dr. Astronaudi korral dr=h ja r=6,77×106m. Asetades need andmed valemisse 13-16, saame
kus Maa massi väärtus on võetud lisast C. Tulemus näitab, et Maa poole suunatud raskuskiirendus astronaudi jalgade juures on veidi suurem kui raskuskiirendus tema pea juures. Raskuskiirenduste erinevus püüab venitada astronaudi keha, aga kuna erinevus on väga väike, siis pole venitamine märgatav.
(b) Kui astronaut tiirleb samasuguse raadiusega orbiidil r=6,77×106m, jalad „allpool”, ümber musta augu, mille mass Mauk=1,99×1031kg ( Päikese massi), siis kui palju sel juhul erineb raskuskiirendus tema pea ja jalgade juures? Mustal augul on teatav piirpind (sündmuste horisont), mille raadius on Rauk=2,95×104m. Mitte miski, isegi mitte valgus, ei suuda sellelt pinnalt või selle pinnaga piiratud ruumiosast lahkuda. Paneme tähele, et astronaut on sellest pinnast tublisti kaugemal ().
Arvutused: Ka siinsel juhul võime astronaudi jalgade ja pea -suunalise kauguse keskpunktist lugeda erinevaks vaid diferentsiaali dr võrra ning seega saame kasutada valemit 13-16. Valemis 13-16 tuleb Maa mass MMaa asendada musta augu massiga Mauk=1,99×1031kg ja siis saame arvutada
See tähendab, et musta augu poole suunatud raskuskiirendus astronaudi jalgade juures on märgatavalt suurem kui tema pea juures. Raskusjõu püüd astronaudi keha venitada on talutav, aga valulik. Kui ta liiguks mustale augule lähemale, muutuks venitus drastiliselt suuremaks.
Newtoni kihiteoreemi saab rakendada ka olukorras, kus punktosake paikneb seespool ühtlast ainekihti, ja tulemuse võib sõnastada järgmiselt:
Gravitatsiooniline resultantjõud, millega ühtlane ainekiht mõjutab seespool seda kihti asuvat osakest, on null.
Hoiatus: See ei tähenda, et kihi elementide poolt osakesele mõjuvad gravitatsioonijõud kaovad müstilisel viisil. See tähendab hoopiski seda, et osakesele kihi kõigi elementide poolt mõjuvate jõuvektorite summa on null.
Kui Maa mass oleks jaotunud ühtlaselt, siis oleks osakesele mõjuv gravitatsioonijõud maksimaalne Maa pinnal ja kahaneks, kui osake liiguks planeedist eemale. Kui osake liiguks planeedi sisemuse poole, näiteks sügava kaevanduse šahti, siis gravitatsioonijõud muutuks kahel põhjusel. (1) Jõud kasvaks, sest osake liigub lähemale Maa keskpunktile. (2) Jõud kahaneks, sest järjest paksenev ainekiht, mis jääb väljapoole osakese radiaalsuunalist asukohta, ei osale osakesele mõjuvas resultantjõus.
Kui Maa oleks ühtlane kera, siis teine efekt domineeriks – osakesele mõjuv jõud kahaneks pidevalt ning saaks nulliks, kui osake jõuab Maa keskpunkti. Kuna aga Maa ei ole ühtlane, siis tegelikul liikumisel Maa keskpunkti poole osakesele mõjuv jõud algul kasvab, saavutab maksimumi teatud sügavusel ja hakkab seejärel kahanema.
Näidisülesanne 13-4
Lahendus
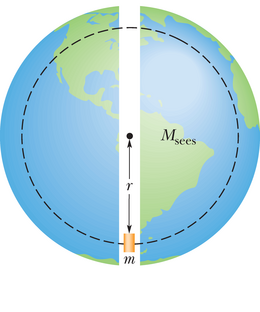
JUHTMÕTTED Newtoni kihiteoreem annab meile kolm ideed:
- Kaugusel Maa keskpunktist on teatav hulk massist väljaspool selle raadiusega kerapinda ja seega ei osale kapslile mõjuvas gravitatsioonijõus.
- Üksnes see osa Maa massist, mis jääb sissepoole kerapinda raadiusega , osaleb kapslile mõjuvas gravitatsioonijõus.
- Maa massi seda osa , mis jääb sissepoole kapsli asukohta, võime vaadelda kui Maa keskpunktis asuvat punktosakest massiga .
Arvutused: Toodud kolm juhtmõtet lubavad kapslile mõjuva jõu tugevuse arvutamiseks kasutada valemit 13-1,
Selleks et esitada mass raadiuse kaudu, arvestame, et raadiusega kerapinna sisse jääv ruumala Vsees on (43)πρ3. Kuna me eeldasime, et Maa tihedus on ühtlane, siis on ta esitatav valemiga ρsees=Msees/Vsees ja see on võrdne Maa tihedusega . Seega saame jaoks valemi
Asetades selle avaldise valemisse 13-17, saame
See seos ütleb meile, et kapslile mõjuv jõud muutub võrdeliselt kapsli kaugusega Maa keskpunktist. Seega kahanedes kahaneb ka jõud , kuni see saab nulliks Maa keskpunktis (vastupidi Griffithi kirjeldusele). Vähemalt see on Griffithi jutus õige, et Maa keskpunktis saab resultantjõud nulliks.
Võrrandi 13-19 võib esitada ka jõuvektori ja kapsli radiaalse kohavektori kaudu (radiaaltelg algab Maa keskpunktis). Tähistades üksnes konstante sisaldava liikme 4πGmρ/3 tähega , saame valemi 13-19 esitada kujul
kus lisatud miinusmärk tähendab seda, et vektorid ja on vastassuunalised. Valemil 13-20 on sama kuju kui Hooke’i seadusel (valem 7-20, →F=−k→d). Niisiis, meie ulmelise loo raames hakkaks kapsel Maa keskpunkti ümber võnkuma nagu klots vedru küljes: kukkunud lõunapooluselt Maa keskpunkti, jätkaks ta oma liikumist (nagu Griffith ütles) keskpunktist põhjapooluseni ja siis jälle tagasi, korrates selliseid võnkeid igavesti.
Punktis 8-4 vaatasime gravitatsiooniliselt seotud süsteemi, mis koosnes punktmassist ja Maast, ning leidsime selle süsteemi gravitatsiooni potentsiaalse energia. Selleks et hoida punktosakesele mõjuvat gravitatsioonijõudu konstantsena, tuli eeldada, et osake asub maapinna lähedal. Seejärel valisime mingi selle süsteemi tugioleku, mille gravitatsiooni potentsiaalse energia võtsime võrdseks nulliga. Sageli valitakse nullnivooks olek, kus osake on maapinnal. Sel juhul hakkaks maapinnast kõrgemal olevate osakeste gravitatsiooni potentsiaalne energia vähenema, kui kaugus osakeste ja maapinna vahel väheneks.
Üldistame nüüd seda käsitlust ja vaatame kahest osakesest koosneva süsteemi gravitatsiooni potentsiaalset energiat , kus osakeste massid on vastavalt ja ning nendevaheline kaugus on . Edasi valime süsteemi tugioleku, millele vastava potentsiaalse energia loeme nulliks. Selleks et valemeid lihtsustada, valime tugiolekuks süsteemi sedavõrd suure osakestevahelise kaugusega , et võime seda käsitleda lõpmata suurena. Ka sel juhul gravitatsiooni potentsiaalne energia väheneb, kui osakestevaheline kaugus väheneb. Et , kui , siis on potentsiaalne energia negatiivne suvalise lõpliku osakestevahelise kauguse korral ning muutub järjest negatiivsemaks, kui osakestevaheline kaugus väheneb.
Eespool öeldut arvestades (vt ka tõestust allpool) kirjutame kahest osakesest koosneva süsteemi potentsiaalse energia avaldise kujul
Paneme tähele, et läheneb nullile, kui läheneb lõpmatusele, ja iga lõpliku korral on negatiivne.
Potentsiaalse energia avaldis 13-21 iseloomustab kahest osakesest koosnevat süsteemi ja ei iseloomusta kumbagi osakest eraldi. Seda energiat ei ole võimalik osakeste vahel ära jagada sellisel viisil, et saaksime öelda, et teatav osa kuulub ühele osakesele ja ülejäänud osa teisele osakesele. Siiski, juhul kui , näiteks kui süsteemiks on Maa massiga ja pall massiga , öeldakse tihti, et kehal massiga on potentsiaalne energia. Me võime sellega leppida, sest juhul, kui pall liigub maapinna lähedal, siis süsteemi pall–Maa potentsiaalse energia muutus ilmneb peaaegu täielikult palli kineetilise energia muutusena ja Maa kineetilise energia muutus on täiesti tühine. Punktis 13-8 vaatleme küsimust Maa orbiidil tiirlevast tehiskaaslasest ja ka seal räägime tehiskaaslase potentsiaalsest energiast, sest tema mass on tühine võrreldes Maa massiga. Kui aga süsteemi moodustavate kehade massid on samas suurusjärgus, siis peame potentsiaalset energiat mõistma kui tervet süsteemi iseloomustavat suurust.
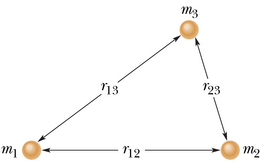
Juhul kui vaadeldav süsteem koosneb rohkemast kui kahest osakesest, siis peame vaatlema võimalikke osakesepaare ühekaupa ning arvutama igale osakesepaarile vastava gravitatsiooni potentsiaalse energia valemist 13-21, kusjuures süsteemi ülejäänud osakeste olemasolu pole vaja arvestada. Kogu süsteemi potentsiaalse energia saamiseks tuleb kõikidele osakesepaaridele vastavad potentsiaalsed energiad algebraliselt liita. Näitena vaadelgem joonisel 13-9 kujutatud kolmest osakesest koosnevat süsteemi. Rakendame valemit 13-21 kõigile kolmele paarile, summeerime paaride potentsiaalsed energiad ning saame kogu süsteemi potentsiaalse energia kujul
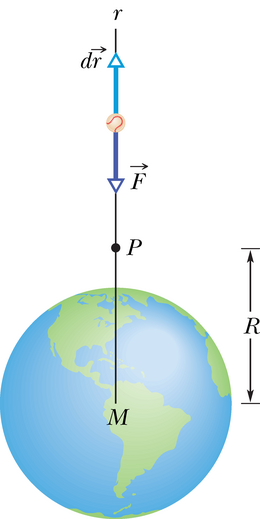
Lööme palli Maast eemale mööda vertikaalset trajektoori, nii nagu on kujutatud joonisel 13-10. Leiame palli gravitatsiooni potentsiaalse energia avaldise punktis , mis asub kaugusel Maa keskpunktist. Kõigepealt arvutame töö , mida teeb gravitatsioonijõud selleks, et viia pall punktist suurele (lõpmatule) kaugusele Maast. Kuna gravitatsioonijõud ei ole konstantne (jõu tugevus sõltub kaugusest ), siis tuleb töö leidmiseks kasutada punktis 7-8 kirjeldatud protseduuri – integreerimist. Töö avaldis vektorkujul on antav integraaliga
Integraalimärgi all on jõuvektori ja palli liikumise suunalise lõpmata väikese nihkevektori skalaarkorrutis. Seda saab avaldada kujul
kus on nurk vektorite ja vahel. Vektorid ja on vastassuunalised ja seega . Asendades jõu avaldise valemist 13-1, saame valemi 13-24 kirjutada
kus on Maa mass ja on palli mass.
Asetame selle avaldise valemisse 13-23 ning integreerime, saame
kus on töö, mida tuleb teha selleks, et liigutada palli punktist (kauguselt ) lõpmatusse. Valem 8-1 () ütleb meile, et töö on võimalik esitada ka potentsiaalse energia kaudu
Potentsiaalne energia lõpmatuses on null (), on potentsiaalne energia punktis ja töö on antud valemiga 13-25, seega saame kirjutada
Asendades selles valemis tähise tähisega , saame valemi 13-21, mida oligi tarvis tõestada.
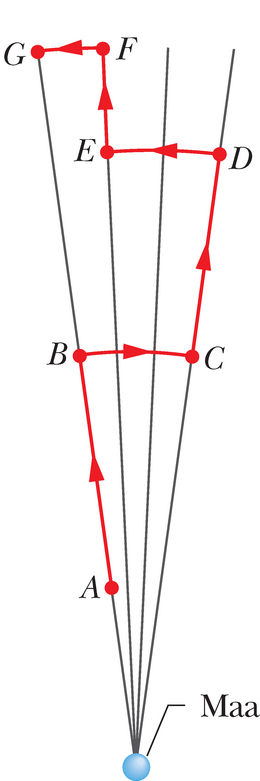
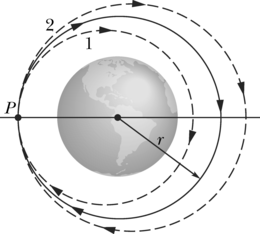
Joonisel 13-11 kujutatud juhul liigub pall punktist punkti mööda teed, mis koosneb kolmest radiaalsest liikumisest ja kolmest liikumisest mööda ringjoone kaart (keskpunktiga Maa tsentris). Meid huvitab Maa gravitatsioonijõu poolt tehtav summaarne töö , mida on tarvis teha palli liigutamiseks punktist punkti . Piki ringjoone kaart liikumisel tehtud töö on null, sest kaare igas punktis on jõuvektor risti nihkevektoriga. Seega on summaarne töö võrdne nende kolme töö summaga, mida jõud teeb radiaalsuunalistel liikumistel.
Kujutleme nüüd, et ringjoone kaared tõmbuvad kokku lõpmata väikesteks. Sel juhul liiguks pall otse punktist punkti mööda ühte radiaalset teed. Kas see muudab tehtud tööd ? Ei muuda, sest liikumisel mööda ringjoone kaari tööd ju ei tehtud ja seega nende kõrvaldamine tööd ei muuda. Liikumistee punktist punkti on sel juhul küll teistsugune, aga jõu poolt tehtud töö on sama.
Me vaatlesime töö sõltumatust trajektoori valikust üldiselt punktis 8-3. Praeguse arutelu võime sealtoodu põhjal kokku võtta väitena, et gravitatsioonijõud on konservatiivne jõud. See tähendab, et gravitatsioonijõu poolt tehtud töö osakese liigutamisel mingist algpunktist mingisse lõpp-punkti ei sõltu sellest, millist teed mööda osake nende punktide vahel liigub. Valemist 8-1 saame, et gravitatsiooni potentsiaalse energia muut liikudes punktist punkti on esitatav valemiga
Kuna konservatiivse jõu poolt tehtud töö on liikumisteest sõltumatu, siis on ka potentsiaalse energia muut liikumisteest sõltumatu.
Valemi 13-21 tõestuses tuletasime potentsiaalse energia kui funktsiooni , kasutades antud jõu avaldist . Peaksime õppima tegema ka vastupidi – leidma jõu avaldise, kui on antud potentsiaalse energia funktsioon. Meenutades valemit 8-22 (), kirjutame
See ongi tuntud Newtoni gravitatsiooniseadus (valem 13-1). Miinusmärk tähendab seda, et massile mõjuv jõud on suunatud radiaalselt sissepoole, massi poole.
Kui tulistada mürsk vertikaalselt üles, siis enamasti ta liikumine järjest aeglustub, siis mürsk peatub hetkeks ja lõpuks langeb tagasi Maale. Kui aga mürsk saab teatud miinimumväärtusest suurema algkiiruse, siis tema liikumine küll aeglustub, aga teoreetiliselt saab kiirus nulliks alles lõpmata kõrgel. Seda minimaalset algkiirust nimetatakse (Maa) paokiiruseks.
Vaatleme mürsku massiga m, mis lastakse planeedi (või mõne teise taevakeha või süsteemi) pinnalt üles paokiirusega . Mürsul on kineetiline energia () ja potentsiaalne energia , mis on antud valemiga 13-21:
kus on planeedi mass ja planeedi raadius.
Kui mürsk jõuab lõpmatusse, siis ta peatub ja tema kineetiline energia on null. Sama juhtub ka potentsiaalse energiaga, sest nii oleme valinud süsteemi gravitatsiooni potentsiaalse energia nullnivoo. Seega on lõpmatuses mürsu koguenergia null. Kuid siis pidi vastavalt energia jäävuse seadusele mürsu koguenergia olema null ka Maa pinnal ja seega saame kirjutada
Avaldades sellest seosest kiiruse, saame
Paneme tähele, et paokiirus ei sõltu sellest, mis suunas mürsk on planeedi pinnalt tulistatud. Siiski on paokiirust kergem saavutada juhul, kui mürsk tulistatakse suunas, kuhu liigub Maa pöörlemise tõttu mürsu stardiplats. Näiteks stardivad raketid Canaverali neemelt ida suunas, sest neem liigub Maa pöörlemise tõttu ida suunas kiirusega .
Valemit 13-28 võib kasutada paokiiruse leidmiseks iga taevakeha jaoks, asendades sinna vastava keha massi ja raadiuse . Tabelis 13-2 on esitatud mõned näited taevakehade paokiirustest.
Näidisülesanne 13-5
Lahendus
JUHTMÕTTED Kui jätame arvestamata atmosfääri mõju asteroidile, siis on süsteemi Maa–asteroid mehaaniline energia jääv kogu asteroidi langemise aja. Seega on asteroidi mehaaniline energia lõppolekus (Maa pinnani jõudmisel) võrdne algoleku mehaanilise energiaga. Kineetilise energia ja potentsiaalse energia jaoks saame kirjutada võrrandi
Kui loeme vaadeldava süsteemi isoleerituks, siis peab selle süsteemi liikumishulk samuti olema jääv. Seega peab asteroidi liikumishulga muutus olema võrdne ja vastasmärgiline Maa liikumishulga muutusega. Kuna aga Maa mass on palju suurem kui asteroidi mass, siis on Maa kiiruse muutus võrreldes asteroidi kiiruse muutusega tühine. Järelikult on tühine ka Maa kineetilise energia muutus. Seega võime valemis 13-29 olevat kineetilist energiat käsitleda asteroidi kineetilise energiana.
Arvutused: Olgu asteroidi mass ja Maa mass (). Asteroid on algul kaugusel ja lõpuks kaugusel Maa keskpunktist (). Asetades valemisse 13-29 potentsiaalse valemist 13-21 ja kineetilise energia , saame
Teisendades ja asendades tuntud suurused, saame
millest leiame otsitava lõppkiiruse
Sellise kiirusega vastu Maad põrkav asteroid ei pea olema eriti suur, et tekitada märkimisväärseid purustusi. Kõigest läbimõõduga asteroidi kokkupõrkel Maaga vabaneks sama palju energiat, kui vabanes Hirošimale heidetud tuumapommi korral. Muret tekitab asjaolu, et Maa orbiidi lähedal liigub ligikaudu miljonit sellise läbimõõduga asteroidi. Aastal 1994 sisenes üks niisugune asteroid Maa atmosfääri ja plahvatas 20km kõrgusel Vaikse ookeani lõunaosa kohal, vallandades tuumaplahvatuse hoiatussignaali kuuel sõjalise otstarbega satelliidil. Kokkupõrge asteroidiga, mille läbimõõt oleks 500m (Maa orbiidi lähedal võib neid olla miljon), hukutaks praeguse tsivilisatsiooni ja hävitaks peaaegu kogu inimkonna.
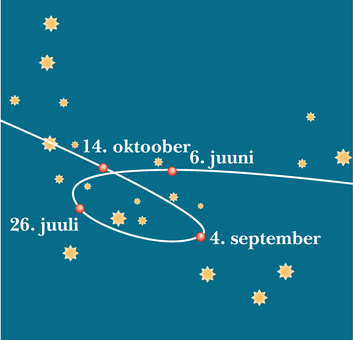
Planeetide näiv liikumine tähtede suhtes on olnud mõistatuseks aegade algusest. Marsi liikumine mööda silmuseid (joonis 13-12) oli eriti kummaline. Aastaid kestnud uurimistöö tulemusena sõnastas Johannes Kepler (1571–1630) empiirilised seadused, mis kirjeldavad neid liikumisi. Tycho Brahe (1546–1601) – viimane kuulus astronoom, kes tegi vaatlusi teleskoopi kasutamata – kogus suure hulga andmeid, mille alusel Kepleril õnnestus tuletada kolm seadust planeetide liikumise kohta, mis praegu on tuntud Kepleri seadustena. Hiljem näitas Newton (1642–1727), et Kepleri seadused järelduvad tema sõnastatud gravitatsiooniseadusest.
Järgnevalt käsitleme ükshaaval kõiki kolme Kepleri seadust. Olgugi et me sõnastame need seadused Päikese ümber tiirlevate planeetide jaoks, kehtivad nad iga massiivse keha ümber tiirlevate kehade, näiteks ümber Maa tiirlevate looduslike ja ka tehislike satelliitide jaoks.
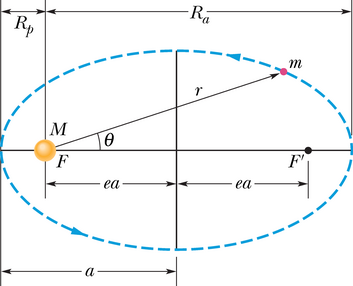
Joonisel 13-13 on kujutatud planeeti massiga liikumas elliptilisel orbiidil ümber Päikese, mille mass on . Me eeldame, et , ja see tähendab, et süsteemi planeet–Päike massikese asub ligikaudu Päikese keskpunktis.
1. Orbiitide seadus Kõik planeedid liiguvad mööda elliptilisi orbiite, mille ühes fookuses on Päike.
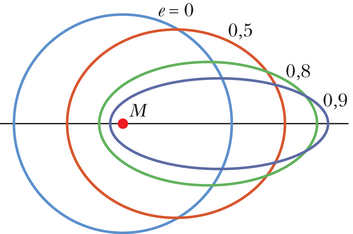
Joonisel 13-13 kujutatud orbiiti kirjeldavad täielikult tema suur pooltelg ja tema ekstsentrilisus , mis on defineeritud nii, et suurus ea oleks võrdne kaugusega ellipsi keskpunktist ükskõik kumma fookuseni, või . Nulliga võrdne ekstsentrilisus vastab ringjoonele, mille korral fookused langevad kokku ja asuvad ringjoone keskpunktis. Planeetide orbiitide ekstsentrilisused ei ole suured ja seetõttu on nad õiges proportsioonis joonistatuna väga lähedased ringjoonele. Näitlikkuse huvides on joonisel 13-13 kujutatud ellipsi ekstsentrilisus liialdatult suur, . Maa orbiidi ekstsentrilisus on ainult .
Kvalitatiivselt tähendab Kepleri teine seadus seda, et planeet liigub kõige aeglasemalt, kui ta on Päikesest kõige kaugemal, ja kõige kiiremini, kui ta on Päikesele kõige lähemal. Tuleb välja, et Kepleri teine seadus on täielikult ekvivalentne pöörlemishulga (impulsimomendi) jäävuse seadusega. Tõestame selle.
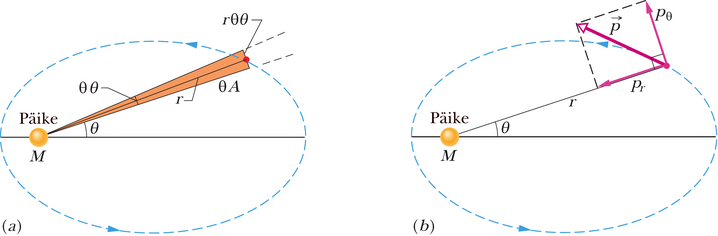
Joonisel 13-14a kujutatud varjutatud kiilu pindala on ligikaudu võrdne Päikest ja temast kaugusel olevat planeeti ühendava mõttelise joone poolt ajavahemiku jooksul kaetud pindalaga. Varjutatud kiilu pindala on ligikaudu võrdne kolmnurga pindalaga, mille alus on ja kõrgus on . Kuna kolmnurga pindala on võrdne poolega aluse ja kõrguse korrutisest, siis saame . See avaldis pindala jaoks muutub seda täpsemaks, mida enam ajavahemik (ja seega ka ) läheneb nullile. Varjutatud pindala muutumise hetkkiirus on seega
kus on Päikest ja tema ümber tiirlevat planeeti ühendava mõttelise joone nurkkiirus. Joonisel 13-14b on kujutatud planeedi liikumishulga vektor ning selle vektori radiaalsuunaline ja sellega risti olev komponent. Valemi 11-20 (L=rp⊥) kohaselt on Päikese ümber tiirleva planeedi pöörlemishulga vektori suurus määratud kauguse ja liikumishulga vektori radiaalsuunaga risti oleva komponendi →p⊥ korrutisega. Massiga planeedi jaoks saame seega
kus me oleme asendanud suurusega (valem 10-18). Elimineerides valemitest 13-30 ja 13-31 suuruse , saame
Vastavalt Kepleri teisele seadusele on suurus konstantne ja seega järeldub valemist 13-32, et ka peab olema konstantne, mis tähendabki seda, et pöörlemishulk on jääv. Näeme, et Kepleri teine seadus on tõepoolest ekvivalentne pöörlemishulga jäävuse seadusega.
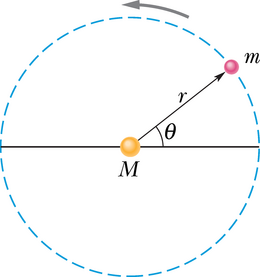
Selles veendumiseks vaatleme ringorbiiti raadiusega (ringjoone raadiuse võtame võrdseks ellipsi suure poolteljega), mida on kujutatud joonisel 13-15. Rakendame Newtoni teist seadust () orbiidil liikuvale planeedile, saame
3. Perioodide seadus Planeedi tiirlemisperioodi ruut on võrdeline tema orbiidi suure pooltelje kuubiga.
Siin oleme jõu tugevuse asendanud valemist 13-1 ning tsentripetaalkiirenduse asendanud suurusega , kasutades valemit 10-23. Kui nüüd valemi 10-20 põhjal asendada suurus ω suurusega , kus on tiirlemisperiood, saamegi Kepleri kolmanda seaduse:
Sulgudes olev liige on konstant, mis sõltub ainult tsentraalkeha massist , mille ümber planeet tiirleb.
Valem 13-34 jääb kehtima ka elliptiliste orbiitide korral, kui me asendame ringjoone raadiuse ellipsi suure poolteljega . Kolmas seadus ennustab, et suhe on ligikaudu ühesugune kõigi sama tsentraalkeha ümber tiirlevate planeetide jaoks. Tabelis 13-3 esitatud andmed näitavad, kui täpselt see kehtib Päikesesüsteemi planeetide korral.
Halley komeedi ümber Päikese tiirlemise periood on aastat. Komeedi periheeli kaugus ehk lähim kaugus Päikeseni on ja selle punkti läbis see 1986. aastal. Tabelist 13-3 nähtub, et komeedi periheel asub Merkuuri ja Veenuse orbiidi vahel.
(a)
Lahendus
JUHTMÕTTED Jooniselt 13-13 näeme, et , kus on orbiidi suur pooltelg. Seega saame leida , kui teame orbiidi suurt pooltelge . Vastavalt perioodide seadusele (valem 13-34) saame orbiidi suure pooltelje avaldada komeedi tiirlemisperioodi kaudu, kui asendame valemis 13-34 suuruse suurusega .
Arvutused: Tehes eespool mainitud asenduse ning seejärel avaldades valemist 13-34 suuruse , saame
Paneme Päikese massi 1,99×1030kg ja komeedi perioodi aastat ehk valemisse 13-35 ning leiame, et a=2,7×1012m. Nüüd saame arvutada
Tabelist 13-3 nähtub, et komeedi afeeli kaugus on natuke väiksem kui Pluuto orbiidi suur pooltelg. Komeet ei liigu seega Päikesest kaugemale kui Pluuto.
Näidisülesanne 13-7
Lahendus
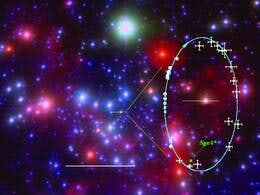
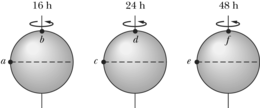
JUHTMÕTE Tiirlemisperiood ja orbiidi suur pooltelg a on seotud Sagittarius A* massiga vastavalt Kepleri perioodide seadusele. Asendades valemis 13-34 ringorbiidi raadiuse elliptilise orbiidi suure poolteljega , saame
Arvutused: Avaldades seosest 13-36 suuruse ja asendades teadaolevad andmed, saame kirjutada
Selleks et saada aimu, mis laadi objekt Sagittarius A* olla võiks, jagame selle massi läbi Päikese massiga (P¨aike=1,99×1030kg) ja saame, et
Seega on Sagittarius A* mass 3,7 miljonit korda suurem kui Päikese mass, aga sellest hoolimata on ta nähtamatu! Tegemist on äärmiselt kompaktse massiivse objektiga. Asjaolu, et tohutu mass on koondunud väga väikeste mõõtmetega objektiks, viitab võimalusele, et tegemist on ülimassiivse musta auguga. Järjest rohkem koguneb tõendeid selle kohta, et ülimassiivsed mustad augud asuvad enamiku galaktikate tsentrites. (Tähtede liikumist ümber Sagittarius A* näitavaid videoklippe on võimalik leida ka Internetist, näiteks otsides fraasi „black hole galactic center”).
Satelliidi liikumisel mööda elliptilist orbiiti ümber Maa muutuvad perioodiliselt nii tema kiirus, mis määrab tema kineetilise energia , kui ka tema kaugus Maa keskpunktist, mis määrab tema gravitatsiooni potentsiaalse energia . Satelliidi mehaaniline koguenergia jääb sellest hoolimata konstantseks. (Kuna satelliidi mass on palju väiksem Maa massist, siis loeme süsteemi Maa–satelliit energiad ja määratuks üksnes satelliidi vastavate energiate poolt.)
Süsteemi potentsiaalne energia on antud valemiga 13-21
(, kui satelliidi kaugus Maast on lõpmata suur). Siin on satelliidi orbiidi raadius (tehes ajutiselt eelduse, et orbiit on ringjoon), on Maa mass ja on satelliidi mass.
Selleks et leida satelliidi kineetiline energia ringorbiidil, kirjutame Newtoni teise seaduse () kujul
kus on satelliidi tsentripetaalkiirendus. Seejärel saame valemist 13-37 leida kineetilise energia
mis ütleb, et ringorbiidil liikuva satelliidi korral kehtib seos
Orbiidil liikuva satelliidi mehaaniline koguenergia on
ehk
Ringorbiidil oleva satelliidi koguenergia on seega kineetilise energiaga arvuliselt võrdne ja vastasmärgiline:
Elliptilisel orbiidil liikuva satelliidi korral võime tema mehaanilise koguenergia leida, kui asendame valemis 13-40 orbiidi raadiuse vastava elliptilise orbiidi suure pooltelje pikkusega
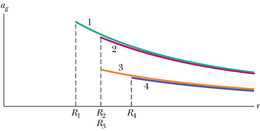
Valem 13-42 ütleb meile, et orbiidil liikuva satelliidi koguenergia sõltub ainult tema orbiidi suure pooltelje pikkusest ja ei sõltu tema orbiidi ekstsentrilisusest . Illustratsiooniks on joonisel 13-17 kujutatud nelja orbiiti, mille suured poolteljed on pikkuselt võrdsed ja järelikult on nendel orbiitidel liikudes satelliidi mehaaniline koguenergia E ühesugune. Joonisel 13-18 on kujutatud ringorbiidil ümber massiivse keha liikuva satelliidi , ja muutust sõltuvana kaugusest .
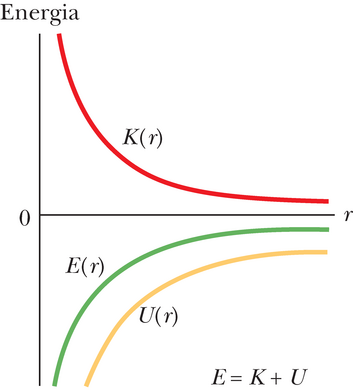
| JOONIS 13-17 Massiga keha ümber on kujutatud nelja erineva ekstsentrilisusega orbiiti. Kõigi nelja orbiidi suured poolteljed on võrdse pikkusega ja seega on võrdne ka nendel orbiitidel liikuvate satelliitide mehaaniline koguenergia . | JOONIS 13-18 Kineetilise energia , potentsiaalse energia ja koguenergia muutus sõltuvana satelliidi ringorbiidi raadiusest . Iga väärtuse korral on ja väärtused negatiivsed, väärtus aga positiivne, kusjuures (ringorbiit, 13-41) . Nii , kui ka väärtused lähenevad nullile, kui r→∞. |
KONTROLLKÜSIMUS 5
Vallatu astronaut laseb keeglikuuli massiga ringorbiidile, mis asub kõrgusel maapinnast.
(a)
Lahendus
JUHTMÕTE Energia saame leida valemist 13-40 (E=−GMm/2r), kuid selleks peame kõigepealt leidma orbiidi raadiuse .
Arvutused: Orbiidi raadius
kus on Maa raadius. Nüüd saame valemist 13-40 leida mehaanilise energia
(b)
Lahendus
JUHTMÕTE Stardiplatvormil ei ole keeglikuul orbiidil ja seega ei saa valemit 13-40 rakendada. Selle asemel peame arvutama E0=K0+U0, kus on keeglikuuli kineetiline energia ja on süsteemi keeglikuul–Maa gravitatsiooni potentsiaalne energia.
Arvutused: Kasutades valemit 13-21, saame suuruse jaoks kirjutada
Kuna Maa pöörleb, siis ka keeglikuul liigub ja seetõttu on tal kineetiline energia . Saab näidata, et on väiksem kui 1MJ ja seega tühine võrreldes -ga. Seega on kuuli mehaaniline energia süstiku stardiplatvormil
Mehaanilise energia suurenemine keeglikuuli viimisel stardiplatvormilt orbiidile on
Sellise energiahulga eest maksame Eesti Energiale paar eurot. Kehade orbiidile viimise kallis hind ei ole niisiis tingitud sellest, et nad saavad juurde palju mehaanilist energiat.
Albert Einstein on öelnud: „Ma olin … Berni patendibüroos, kui äkitselt tekkis mul mõte: „Vabalt langev inimene ei tunne ju iseenda kaalu.” Ma olin jahmunud. See lihtne mõte avaldas mulle sügavat muljet. See ajendas mind tegelema gravitatsiooniteooriaga.”
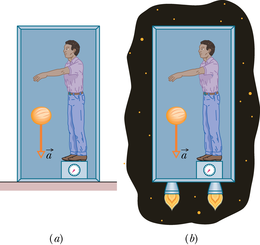
Niimoodi kirjeldas Einstein seda, kuidas ta alustas üldrelatiivsusteooria vormimist. Tema gravitatsiooniteooria (kehade gravitatsioonilise tõmbumise teooria) aluspostulaati nimetatakse ekvivalentsusprintsiibiks ning see väidab, et gravitatsioon ja kiirendus on teineteisega ekvivalentsed. Kui füüsik oleks suletud kinnisesse kasti (joonis 13-19), siis ta ei saaks kindlaks teha, kas kast on maapinnal paigal (mõjutatud ainult Maa gravitatsioonijõu poolt) nagu joonisel 13-19a või liigub kiirendusega tähtedevahelises ruumis (mõjutatud üksnes seda kiirendust tekitava jõu poolt) nagu joonisel 13-19b. Mõlemal juhul tunneb füüsik end ühteviisi ja ka kaalu näit on mõlemal juhul sama. Veelgi enam, kastis vabalt langeval kehal oleks mõlemal juhul võrdse suurusega kiirendus füüsiku suhtes.
Seni oleme gravitatsiooni seletanud kui jõudu, mis mõjub masside vahel. Einstein näitas teistsuguse seletuse võimalikkust: gravitatsioon on tingitud ruumi kõverusest ja seda kõverust tekitavad ruumis paiknevad massiga kehad. (Hiljem näeme, et ruum ja aeg on omavahel seotud, ja et kõverus, mida Einstein silmas pidas, on tegelikult neljamõõtmelise aegruumi kõverus.)
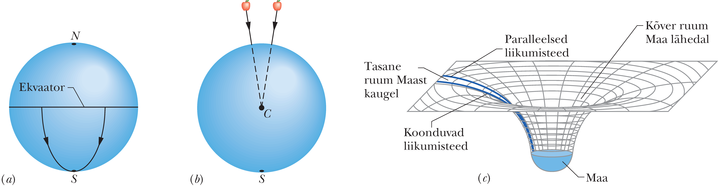
Kujutleda, kuidas ruum (nagu näiteks vaakum) saab olla kõver, on raske. Siin võib meid aidata teatav analoogia. Oletame, et jälgime orbiidilt kahe ekvaatorilt võistlust alustava laeva liikumist. Olgu laevade kaugus teineteisest ekvaatoril 20 km ja suundugu nad lõunapooluse poole (joonis 13-20a). Meremeestele tundub, et laevad liiguvad sirgel ning paralleelsel kursil. Aja jooksul laevad siiski lähenevad teineteisele ja vahetult lõunapooluse lähedal puutuvad kokku. Meremehed laevadel võivad seda lähenemist interpreteerida laevadele mõjuva jõu toimena. See-eest kosmosest vaadatuna näeme, et nad lähenevad lihtsalt sellepärast, et Maa pind, mida mööda nad liiguvad, on kõver. See on meile nähtav, kuna jälgime võidusõitu „väljastpoolt” seda pinda.
Joonisel 13-20b on kujutatud sarnane olukord: kaks õuna, mis on algselt teineteisest mingil kindlal kaugusel ja võrdsel kõrgusel maapinnast, lastakse vabalt langema. Olgugi et paistab, justkui liiguksid õunad mööda paralleelseid trajektoore, siis tegelikult liiguvad nad teineteisele lähemale, sest mõlemad langevad Maa keskpunkti suunas. Me võime õunte liikumist interpreteerida kui Maa gravitatsioonijõu mõju õuntele, kuid me võime seda interpreteerida ka kui õunte liikumist Maa massi tõttu kõverdunud ruumis. Antud juhul me ei näe ruumi kõverana, sest me ei saa minna „väljapoole” seda ruumi, nii nagu saime seda teha juhul, kui vaatlesime laevade liikumist Maa kumeral pinnal. Siiski saame kujutada kõverust nii, nagu on seda tehtud joonisel 13-20c, kus õunad liiguksid mööda pinda, mis kõverdub Maakera massi tõttu.
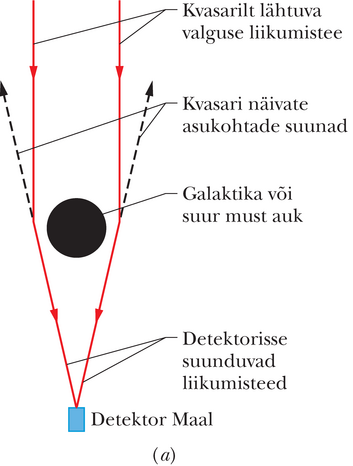
Kui valguskiir möödub Maa lähedalt, siis ta paindub, sest Maa massi tõttu on ruum pisut kõverdunud. Sellist valguskiire paindumist nimetatakse gravitatsiooniläätse efektiks. Juhul kui valguskiir möödub suurema massiga struktuurist, näiteks galaktikast või mustast august, siis paindub tema trajektoor rohkem. Kui selline massiivne struktuur asub meie ja kvasari (väga kauge ja väga hele valgusallikas) vahel, siis tema lähedal paindub kvasarilt lähtunud valguskiir meie poole (joonis 13-21a). Seetõttu paistab meieni jõudev valgus tulevat natuke erinevatest suundadest ja me näeme sedasama kvasarit kõikides nendes suundades. Mõnedel juhtudel sulanduvad need vaadeldavad kvasarite kujutised kokku ja moodustavad hiiglasliku helendava kaare, mida nimetatakse Einsteini rõngaks (joonis 13-21b).
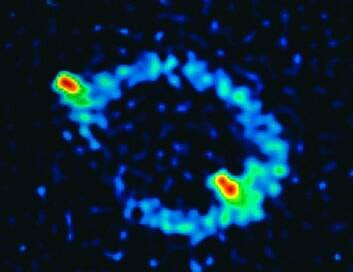
| JOONIS 13-21 (a) Kui kaugelt kvasarilt lähtuv valgus möödub galaktikast või massiivsest mustast august, siis on ta liikumistee kõverdunud, sest galaktika või musta augu mass kõverdab ruumi enda läheduses. Juhul kui kvasarilt lähtuv valgus registreeritakse, siis paistab see valgus pärinevat objektilt, mis asub kõverdunud trajektooride pikendusel (joonisel kriipsjoon). | JOONIS 13-21 (b) Niisugusena paistab MG1131+0456 nime kandev Einsteini rõngas teleskoobi arvuti ekraanil. Valgusallikas (tegelikult raadiolainete allikas) asub kaugel nähtamatu galaktika taga, mis tekitab „helendava” rõnga ja ka valgusallika kaks eredamat kujutist rõngal. (Avaldatud National Radio Astronomy Observatory loal.) |
Kas me peaksime võtma gravitatsiooni kui massiivsete kehade poolt tekitatud aegruumi kõveruse ilmingut või lihtsalt masside vahel mõjuvat jõudu? Või peaksime hoopiski pidama gravitatsiooni nähtuseks, mille kandjaks on teatud tüüpi hüpoteetiline alusosake, mida nimetatakse gravitoniks? Me lihtsalt ei tea seda.
Ühtlase kerakihi gravitatsioon
Valem 13-1 on vahetult rakendatav vaid punktosakeste korral. Gravitatsioonijõu ruumiliste kehade vahel saame leida, kui jagame kehad lõpmata väikesteks osadeks ning seejärel summeerime (integreerime) gravitatsioonijõud kõigi nende osade vahel. Kui vaadeldav k
Kepleri seadused
Gravitatsiooniline külgetõmme hoiab Päikesesüsteemi koos ja teeb võimalikuks nii looduslike kui tehislike satelliitide tiirlemise ümber Maa. Sellist tüüpi liikumised on kirjeldatud Kepleri kolme seadusega, mis kõik järelduvad Newtoni liikumi
Einsteini graviatsiooniteooria
Einstein täheldas, et gravitatsioon ja kiirendus on ekvivalentsed. See ekvivalentsusprintsiibina tuntud väide viis ta gravitatsiooniteooriani (üldrelatiivsusteooriani), mis seletab gravitatsiooni ruumi kõveruse kaudu.