Magnetvoo mõiste

J.2.24 Magnetvoo sõltuvus nurgast β magnetvälja suuna (B) ja juhtmekeeru pinna normaali (n) vahel: a) β = 0, b) 0 < β < π/2, c) β = π/2.

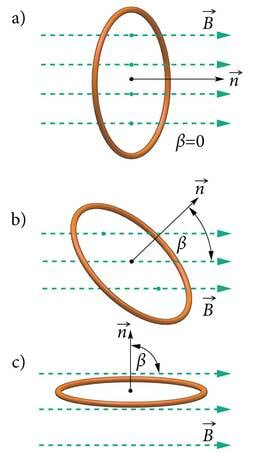
Ülalkirjeldatud katsete tulemuste kokkuvõtlikuks esitamiseks on võetud kasutusele füüsikaline suurus nimega magnetvoog. Magnetvoog $Φ$ näitab, millisel määral läbivad magnetvälja jõujooned vaadeldavat pinda selle pinna suuruse ja asendi tõttu magnetväljas. Piltlikult öeldes näitab magnetvoog pinda läbivate jõujoonte arvu. Loomulikult on see arv eelkõige määratud jõujoonte tihedusega, mida teatavasti iseloomustab magnetinduktsioon. Mingit kindlat pinda läbib joonte suurema tiheduse korral rohkem jõujooni. Magnetvoog läbi vaadeldava pinna on võrdeline magnetinduktsiooniga $B$ . Samas läheb pinnast rohkem jõujooni läbi ka siis, kui pind ise on suurem ning jääb seetõttu jõujoontele rohkem "ette". Magnetvoog on võrdeline pinna pindalaga $S$ . Jõujoonte kindla tiheduse ( $B$ ) ja pinna pindala ( $S$ ) korral sõltub pinda läbiv magnetvoog B-vektori suunast pinna suhtes. Kui pind on $B$ -vektoriga risti ( $β = 0$ ), siis läbib pinda suurim arv jõujooni (J.2.24, a). Sel korral on tegemist suurima magnetvooga. Kui nurk $β$ B-vektori ja pinna normaali vahel erineb nullist, siis on pinda läbivate jõujoonte arv väiksem (J.2.24, b). Seega on väiksem ka magnetvoog. Kui aga nurk $β$ on täisnurk ( $β = π / 2$ ), siis on magnetvälja jõujooned pinnaga paralleelsed. Mitte ükski jõujoon ei läbi pinda. Magnetvoog on null (J.2.24, c). Magnetvoog on maksimaalne nulliga võrduva nurga $β$ korral ning saab ise nulliks, kui see nurk on täisnurk. Seega on magnetvoog võrdeline koosinusega nurgast $β$ magnetvälja suuna ja pinna normaali

Kõik ülaltoodu võib kokku võtta magnetvoo definitsioonivalemisse

(2.5)

Φ = B S cos β

Magnetvoog on skalaarne (suunata), kuid algebraline suurus. Magnetvoo algebralisus tähendab seda, et sõltuvalt magnetvälja suunast võib voog olla nii positiivne kui ka negatiivne suurus. Magnetvoo mõõtühikuks SI-süsteemis on üks veeber ( $1 Wb$ ). Üks veeber on magnetvoog, mis läbib 1 m² suurust magnetvälja suunaga ristuvat pinda, kui välja magnetinduktsioon on $1 T$ . Ühe veebri defineerimisel kasutatakse niisiis valemi 2.5 erijuhtu, mil $β = 0$ , seega $cos β = 1$ ja järelikult $Φ = B S$ , millest

1 Wb = 1 T \cdot 1 m^{2}