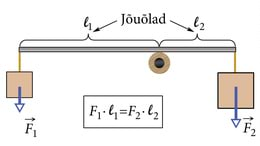
Lihtmehhanismidest täpsemalt, koos arvutustega

Asetades joonlaua pliiatsi peale, saame kõige lihtsama kangi. Joonlaud on tasakaalus, kui pliiats on täpselt joonlaua keskel. Asetades joonlaua otstele erineva massiga koormised, tuleb pliiatsi asukohta (joonlaua toetuspunkti) muuta, et ta oleks jätkuvalt tasakaalus. Mida kaugemal on koormis toetuspunktist, seda suurem on selle pöörav toime, nii et samasuguse toime saavutamiseks tuleb kergem koormis kangi toetuspunktist kaugemale asetada.

Jõu pöörava toime iseloomustamiseks on vaja kasutusele võtta jõu õla mõiste. Jõu õlg on kaugus kangi keskpunktist jõu rakenduspunktini. Jõu õlga tähistatakse tavaliselt tähega l. Kasutades jõu õlga, saame kirja panna kangi reegli ehk kangi tasakaalu tingimuse:

F_{1} \cdot l_{1} = F_{2} \cdot l_{2}

Kui kangi üks jõu õlg on teisest mingi arv kordi pikem, siis võib sinna rakendada sama arv kordi väiksemat jõudu, et kang püsiks tasakaalus.

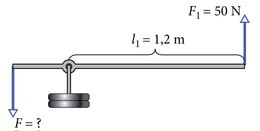
Ühe meetri pikkuse puitvarda ühe otsa külge on riputatud 100grammine raskus ning teise otsa külge 300grammine raskus. Kui kaugel peab olema toetuspunkt varda otsast, kui tahame, et varras oleks tasakaalus? Puitvarda massiga ei ole vaja arvestada.

Lahendus

Kang on tasakaalus, kui mõlemal pool olevate raskuste raskusjõudude ja jõu õlgade korrutised on võrdsed. Tähistame vasakul pool oleva jõu õla $l_{1}$ -ga ning paremal pool $l_{2}$ -ga. Kuna kogu kangi pikkus on $1$ meeter, siis $l_{2} = 1 m - l_{1}$ .

Andmed

$m_{1} = 100 g$
$m_{2} = 300 g$
$l = 1 m - ------ -$
$l_{1} - ?$
$l_{2} - ?$

Arvutused

$F_{1} l_{1} = F_{2} l_{2} \Rightarrow m_{1} g l_{1} = m_{2} g l_{2} \Rightarrow m_{1} l_{1} = m_{2} l_{2}$

Kuna

$l_{2} = l - l_{1}$

siis saame

m_{1} l_{1} = m_{2} (l - l_{1}) \Rightarrow l_{1} = \frac{m_{2} l}{m_{1} + m_{2}}

l_{1} = \frac{300 g \cdot 1 m}{100 g + 300 g} = 0, 75 m = 75 cm

l_{2} = l - l_{1} = 1 m - 0, 75 m = 0, 25 m = 25 cm - ---- - - ---- -

Vastus. Toetuspunkt peab olema raskusest $25 c m$ kaugusel.

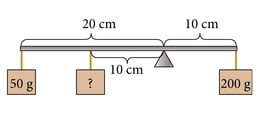
Milline peab olema tundmatu massiga keha mass, et kang oleks tasakaalus?

Lahendus

Paremal pool mõjutab kangi ainult üks koormis. Vasakul pool mõjutab kangi kaks koormist. Kang on tasakaalus, kui vasakul pool olevate koormiste raskusjõudude ja jõu õlgade korrutiste summa on võrdne paremal pool oleva koormise raskusjõu ja jõu õla korrutisega.

Andmed

$m_{1} = 200 g$
$m_{2} = 50 g$
$l_{1} = 10 cm$
$l_{2} = 20 cm$
$l_{3} = 10 cm - --------- -$
$m_{3} - ?$

Arvutused

$F_{1} l_{1} = F_{2} l_{2} + F_{3} l_{3} \Rightarrow m_{1} g l_{1} = m_{2} g l_{2} + m_{3} g l_{3} \Rightarrow m_{1} l_{1} = m_{2} l_{2} + m_{3} l_{3}$

Avaldades viimasest võrrandist $m_{3}$ , saame

$m_{3} = \frac{m_{1} l_{1} - m_{2} l_{2}}{l_{3}}$

$m_{3} = \frac{200 g \cdot 10 cm - 50 g \cdot 10 cm}{10 cm} = 100 g - ---- - - ---- -$

Vastus. Tundmatu massiga keha peab kaaluma $100 g$ , et kang oleks tasakaalus.

Summary

The shoulder of the force $l$ is the distance from the center of the lever to the point of application of the force. The lever rule, or the lever balance condition, can be written with a formula

F_{1} \cdot l_{1} = F_{2} \cdot l_{2}

The balance condition of a lever says that if one force arm of the lever is a certain number of times longer than the other, then the same number of times less force can be applied to it, so that the lever remains in balance.

Probleemülesanded

Kang, mille otstele mõjuvad jõud

8 N

ning

24 N

, on tasakaalus. Kangi üks jõu õlg on

8 c m

. Kui pikk on kang, kui me kangi massi ei arvesta? Kui arvestaksime kangi massi, kas siis oleks kang pikem/lühem võrreldes sellega, kui me kangi massi ei arvestanud?

Hinda, kui palju sa võidad kääridega lõigates jõus. Tee joonis!

Ühtlase kangi pikkus on

2 m

ja mass

10 k g

. Tema parempoolsele otsale mõjub jõud

F_{1} = 50 N

(vt joonist). Kui suurt ja mis suunas mõjuvat jõudu

F

tuleb rakendada kangi vasakpoolsele otsale, et kang oleks tasakaalus?

2 m

kõrge ja

1 m

lai uks püsib uksehingedel, mis on

10 c m

kaugusel ukse ülemisest ja alumisest servast. Ukse mass on

36 k g

. Kui suure jõuga tõmbab uks ülemist hinge horisontaalsuunas?

Näidisülesanne 1

Näidisülesanne 2

The shoulder of power. The condition of equilibrium of the lever