Naturaalarvud on juba väga toredad, aga nendega tuleb esile ka mõningaid probleeme.

Naturaalarve saame omavahel liita ja summaks on alati naturaalarv: näiteks 3 + 4 = 7 või 2 + 10 = 12. Liitmisest võib siin väga vabalt mõelda lihtsalt loendamise raames: keegi annab teie kolmele õunale neli lisaks või näiteks lisaks teile ja kassapidajale siseneb äkiliselt poodi veel 10 tantsulist.

Tore oleks, kui saaksime ka kuidagi kirjeldada olukorda, kus neli õuna jälle tagasi küsitakse või kus 10 tantsulist jälle poest välja kepslevad. Ütlete kohe, et selleks on muidugi lahutamine: 7 – 4 = 3 või 12 – 10 = 2.

Tekib aga probleem: kui mul on ainult 3 õuna, ei saa mult nelja õuna ära võtta ja kui poes on ainult 2 inimest, ei saa sealt 10 ära minna. Seega osasid arve justkui ei saakski omavahel lahutada.

Veider! Mis on need arvud, mis võiksid tähistada midagi, mis on vähem kui mitte midagi?

Ja kuigi pakuti juba varakult välja, et tegelikult võiksid eksisteerida ka arvud 3 – 4 ning 2 – 10, ei tahetud nendega pikka aega leppida. Neid peeti ebaloomulikeks. Mida peaks tähendama see –1, mida mõni pakkus 3 – 4 vastuseks, või –8, mida pakuti 2 – 10 vastuseks? Kui miski eksisteerib, on teda ju vähemalt üks? Kuidas saab olemas olla mitte millestki veel väiksem kogus?

Tänapäeval kahjuks teab mõni seda liigagi hästi, mida negatiivsed arvud tähistada võivad – näiteks võlga! Katsetage internetis oma pangakontoga, ta võib kergesti sattuda ka miinusesse, kui raha liiga agarasti kulutada. Arvust –1 võibki näiteks mõelda kui õunavõlast vanemale vennale...

Sellega, et negatiivsed arvud on täiesti mõistlikud ja isegi loomulikud, lepiti aga alles 19. sajandil. Enne seda kutsuti neid küll absurdseteks, küll räpasteks ja tihti keelduti nendega igasugusest läbikäimisest. Tegelikult on ju negatiivsete arvudega siiski toredam ja ilusamgi – nende abil ei jää arvsirge poolikuks, vaid on kenasti alguse ja lõputa.

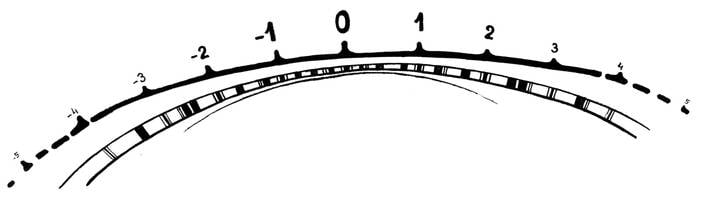
Arvude liitmisest ja lahutamisest võimegi mõelda kui arvsirgel paremale või vasemale poole liikumisest – liites neli, liigume neli sammu paremale; lahutades seitse, seitse sammu vasemale. Kõiki täisarve võime omavahel liita ja lahutada ning alati jälle vastuseks täisarvu saada.

Täisarvude hulka tähistatakse Z-iga.