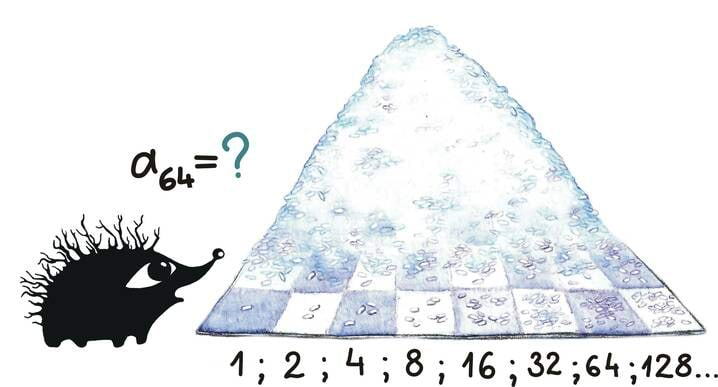
Kui võtta malelaud (8 × 8 ruutu) ning asetada esimesele ruudule üks riisitera, teisele juba kaks riisitera ja igale järgnevale ruudule kaks korda rohkem riisiterasid kui eelnevale, siis mitu tera on lõpuks malelaual kokku?
Legendi kohaselt tutvustas male leiutaja oma uut mängu kohalikule valitsejale. Valitseja oli uue mänguga väga rahul ning lubas leiutajal endale valida ka väärilise tasu. Mees, kellel tarkust puudu ei tulnud, sõnas kuningale: „Auväärt kuningas, ma paluksin endale niipalju riisiterasid, kui on kokku malelaual asetades esimesele maleruudule ühe, teisele kaks, kolmandale neli ning igale järgnevale veel kaks korda enam riisiteri.” Valitseja, kes polnud matemaatika ega matemaatiliste veidrustega sina peal, nõustus kiirelt ettepanekuga, pidades seda vahest isegi solvavalt vähenõudlikuks. Niisiis käskiski ta varahoidjal riisiterade hulga välja arvutada ning leiutajale üle anda. Varahoidjal läks aga terve nädal lubatud riisikoguse leidmiseks. Kui valitseja päris viivituse põhjust, siis varahoidja näitas talle arvutuse lõpptulemust ning selgitas, et sellist tasu ei suudaks kuningas ka oma elu jooksul välja käia. Nüüd oli valitsejale selge, mis leiutajaga pihta hakata: ta lasi nutika mehe nutika pea maha lüüa, et seeläbi igasugustele ülekavaldajatele koht kätte näidata.
Terade arv malelaua ruutudel on järgnev:
Mis on selle jada 64. liige?
Mis on jada 64 esimese liikme summa?
Kui aritmeetilises jadas leitakse iga järgmine liige, liites eelnevale teatud kindla arvu, siis praegu leiame iga järgmise jadaliikme, korrutades eelmist liiget mõne kindla arvuga – meie konkreetsel juhul on selleks arvuks kaks. Selliseid jadasid nimetatakse geomeetrilisteks jadadeks ning arvu, millega iga järgnevat läbi korrutatakse, jada teguriks.
Kui tähistame jada kordajat q-ga ning jada liikmeid nagu ikka tähistusega an, saame analoogiliselt aritmeetilise jada juhuga a2 = a1 · q, seejärel a3 = a2 · q = a1 · q · q, … ning üldisel kujul
Nii võime ka välja arvutada, et malelaua viimasel ruudul peab olema a64 = 1 · 263 = 9 223 372 036 854 775 808 riisitera, mis on umbes 200 miljardit tonni riisi.
Geomeetrilise jada summa valem
Geomeetrilise jada summa valemi leidmiseks on taas kord vaja vaid ühte tähelepanekut ja head kannatust sümbolitemölluga.
Meenutame, et korrutades suvalise jada liikme ai arvuga q, saame jada järgmise liikme ai+1. Seega on jada esimese liikme n summa a1 + a2 + … + an ainult q korda erinev summast a2 + … + an+1, mis on sama jada n liikme summa alates teisest liikmest.
Kuna need jadad erinevad aga ainult kahes liikmes – esimeses neist esineb a1 ja ei esine an+1 ning teises esineb an+1, aga ei esine a1 –, siis on nende jadade summade vahe täpselt võrdne a1 – an+1-ga.
Seega tähistades geomeetrilise jada esimese n liikme summat jällegi Sn abil, võime eelneva arutluse kirja panna kompaktsemalt nii:
Jagades mõlemad pooled läbi q–1-ga, jõuame valemini
mis kasutades jada üldliikme valemit annab tulemuseks
Hääbuv geomeetriline jada
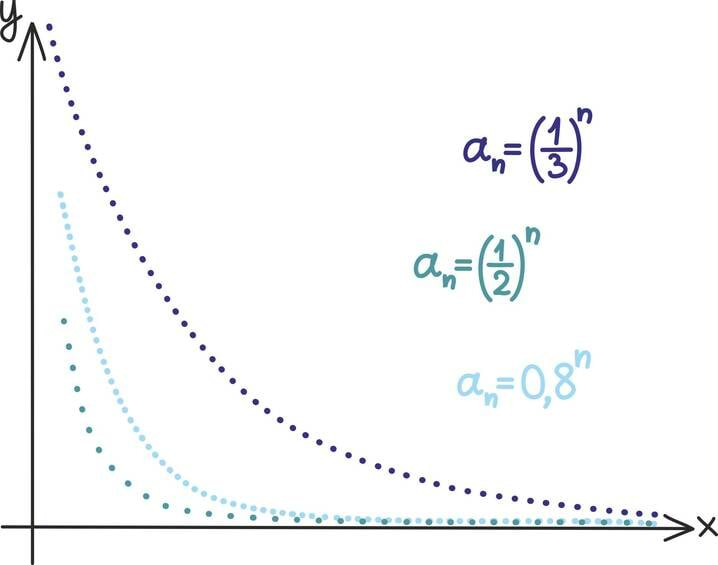
Kui geomeetrilise jada tegur on absoluutväärtuselt väiksem kui üks, nimetatakse saadud jada hääbuvaks geomeetriliseks jadaks.
Näiteks jada 1⁄2; 1⁄4; 1⁄8; 1⁄16 … on hääbuv jada teguriga 1⁄2. Mis on sellise jada kõikide liikmete summa?
Kuna kokku on sellises jadas liikmeid lõpmata palju, võiks ju arvata, et seda summat ei annagi hästi arvutada – ta võiks ju ka olla lõpmatult suur, nii suur, et teda ühe arvuga väljendada ei saagi. Selgub siiski, et tegemist on alati lõpliku ning tihti isegi mitte väga suure arvuga.
Selle probleemiga on tihedalt seotud ka vanakreeka filosoofi Zenoni paradoks, mis väidab järgmist: kui aeglasemale startijale on antud võidujooksus edumaa, siis ei saa kiirem jooksja kunagi aeglasemast jooksjast ette jõuda. Nimelt enne, kui kiirem jooksja aeglasest möödub, peab ta esiteks jõudma punkti, kust aeglasem alustas. Selleks hetkeks on aga aeglasem jooksja juba edasi, järgmisesse punkti jõudnud. Nüüd peab kiirem jooksja enne möödumist hoopis sellesse punkti jõudma. Ja jälle on aeglasem edasi jõudnud. Nii võime lõpmatult jätkata, kuna iga kord, kui kiirem jooksja jõuab aeglasema eelmisesse punkti, on too sealt juba lahkunud.
Ometigi teame, et kiiremad jooksjad mööduvad aeglastest – sellest siis ka põhjus, miks seda arutlust paradoksiks kutsutakse. Võib-olla suudate pärast selle peatüki läbitöötamist näha, miks see „intuitiivne” argument siiski päris hästi paika ei pea.
Pirukad ja hääbuva geomeetrilise jada summa
Vaatleme nüüd enne toodud jada 1⁄2; 1⁄4; 1⁄8; 1⁄16; … pisut lähemalt.
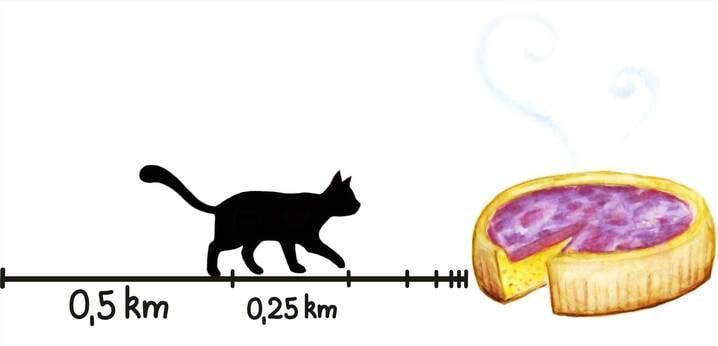
Võime sellest jadast ka muinasjutuliselt mõelda. Oletame, et täpselt kilomeetri kaugusel asub pirukaputka, mille poole hiilib saabasteta kass. Jõudnud poolele teele, on tal läbitud pool kilomeetrit ja läbida jäänud samuti veel pool kilomeetrit. Tähistagu jada esimene liige selle esimese jalutuse pikkust:a1 = 1⁄2 km.
Luuranud hetke, otsustab ta hiilida veel poole jäänud maast – see tähendab pool poolest kilomeetrist ehk veerand kilomeetrit. Tähistame selle jalutuse a2 = 1⁄4 km.
Piilunud veel kord ümberringi ja hinganud sügavalt sisse, otsustab kass kõndida veel poole järele jäänud maast – veel poole veerandist kilomeetrist ehk kaheksandiku kilomeetrit. Tähistame selle jalutuse a3 = 1⁄8 km.
Nii ongi iga edasiliikumine vastavuses ühe jada liikmega ja jada summa on vastavuses kokku läbitud distantsiga. Aga pirukaputkani oli alguses täpselt üks kilomeeter ja seega, kuna kass putkast kaugemale kindlasti ei jõua, ei saa ka jada summa olla suurem kui üks. Tegelikult on see summa täpselt üks, sest pirukaputkani jääv maa muutub nii olematuks, et saabasteta kass paneb tingimata mõne piruka ka nahka.
Seda, et jada summa on lõplik, võib muidugi selgitada ka kasutades eelnevas tärniga osas leitud jada liikmete summa valemit:
Nüüd kui q < 1, siis on see valem igati lõpliku väärtusega ning lisaks kahaneb qn astendaja n kasvades järjest väiksemaks ning läheneb kiiresti nullile.
Nii võime tegelikult näha, et kõikide liikmete summa läheneb arvule
Täpsemalt on S jada Sn piirväärtus [lk 310].
Jada 1⁄2; 1⁄4; 1⁄8; 1⁄16 jaoks on a1 = 1⁄2 ja q = 1⁄2 ning seega on tõesti selle jada summa täpselt 1.
Nimetus
Aritmeetilise jada nime põhjendasime osati hüüdlausega „Aritmeetilise jadaga saab teha aritmeetikat!“. Oleks ju väga tore, kui geomeetrilise jadaga saaks teha geomeetriat... ja mingis mõttes saabki! Nimelt võib mõelda, et alustame ühest teatava pikkusega lõigust ja kõik edasised liikmed lihtsalt suurendavad seda teataval määral. Seega on geomeetriline jada seotud ühe lihtsaima geomeetrilise teisenduse – skaleerimise ehk suurendamise ja vähendamisega.
Kuigi lihtne mõte, võib see vaateviis siiski osutuda kasulikuks. Näiteks pirukapoe külastuse juures illustreerisimegi jada an = 1⁄2n summa lõplikkust ka geomeetriliselt.
Muidugi on lisaks sellele ka geomeetriline jada seotud geomeetrilise keskmisega – jällegi on kolmest järjestikusest liikmest keskmine äärmiste geomeetriliseks keskmiseks [lk 198].