Võrrandil x + 2 = 3 on muutujale antud väga karmid tingimused ning võimalik on täpselt üks lahend: x peab olema võrdne ühega. Geomeetriliselt võime sellest võrrandist mõelda kui sellise arvtelje punkti leidmisest, mis on arvust 3 kahe ühiku võrra vasemal.

Üks viis tingimusi väetimaks muuta ja võrrandile rohkem lahendeid tekitada, on mängu tuua rohkem muutujaid. Näiteks võrrandil x + y = 3 on lahendeid maa ja ilm: iga y-i väärtuse jaoks leidub sobiv väärtus ka x-ile. Kui y on võrdne 2-ga, peab x olema võrdne ühega. Kui y on võrdne 3-ga, peab x võrduma nulliga ja nii edasi.

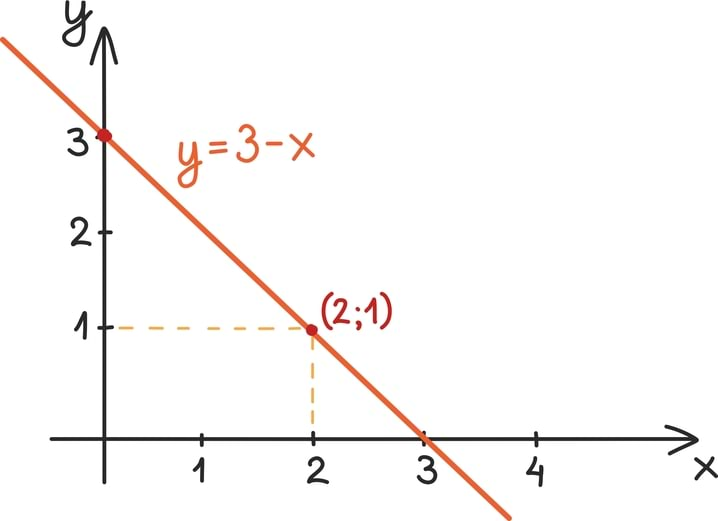
Kõik võrrandi x + y = 3 lahendid on antud arvupaaridena - üks neist ütleb võimaliku muutuja y väärtuse ja teine muutuja x väärtuse. Iga selline arvupaar tähistab aga täpselt ühte punkti arvutasandil: x-i väärtus annab punkti x-koordinaadi ning y-i väärtus punkti y-koordinaadi.

Kui hakkame kõiki neid punkte joonistama, näeme, et nad otsustavad kõik ennast kenasti ühele sirgele ritta seada.

Selgub, et iga kahe muutujaga lineaarne võrrand (mõlema muutuja aste on üks) kirjeldabki täpselt ühte sirget tasandil ja vastupidi ka: kui meile on antud üks sirge tasandil, võime kirjeldada teda kahe muutujaga lineaarse võrrandi abil.

Kõikvõimalikud sirged tasandil oskame kergesti joonistada, kõikvõimalikud kahe muutujaga lineaarvõrrandid on aga antud järgmise kujuga:

Siin on a, b lihtsalt suvalised reaalarvulised kordajad ning c reaalarvuline vabaliige.

See seos on päris kihvt! Meil on ühelt poolt midagi geomeetrilist, joon, mida võime pliiatsi või pastakaga paberile vedada, ning teiselt poolt kuivana näiv võrrand ja ometigi kirjeldavad mõlemad sama matemaatilist objekti!

Ka praktilisema poole pealt on see seos vägagi kasulik, kuna võimaldab tingimusi ja seoseid kirjeldada nii geomeetria kui võrrandite keeles. Seega kui sirgel on mõni omadus, siis peab see vastav omadus olema kirjeldatav ka võrrandite keeles ja vastupidi.

Oletame näiteks, et meie geomeetriliseks omaduseks on teadmine, et sirge läbib punkti null. Milline oleks see omadus võrrandite keeles?

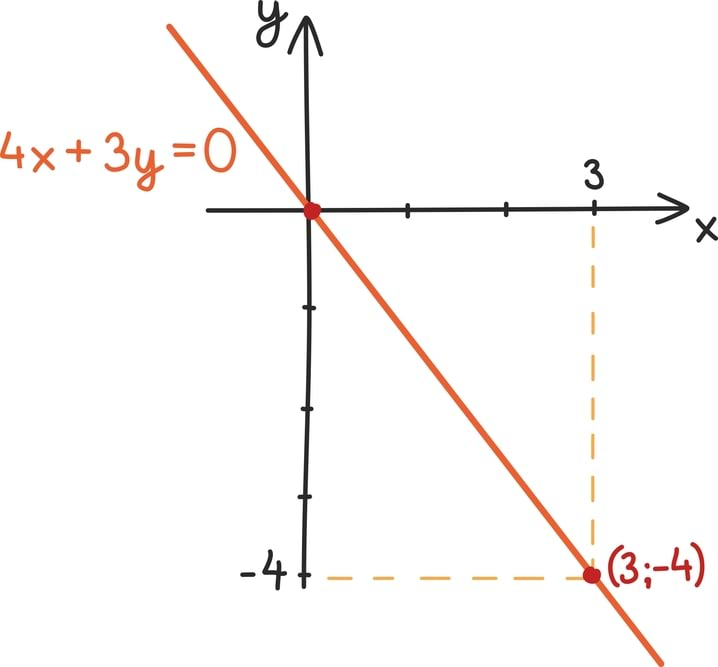
Kui sirge läbib punkti null, siis rahuldab arvupaar (0; 0) võrrandi tingimusi. Sisestades x = 0 ja y = 0 võrrandi üldkujusse, saame, et 0 = c. Seega kui sirge läbib punkti null, puudub vastaval võrrandil vabaliige ning sellise võrrandi võib kirja panna kujul ax + by = 0. Näiteks joonistatud sirge võrrand on 4x + 3y = 0

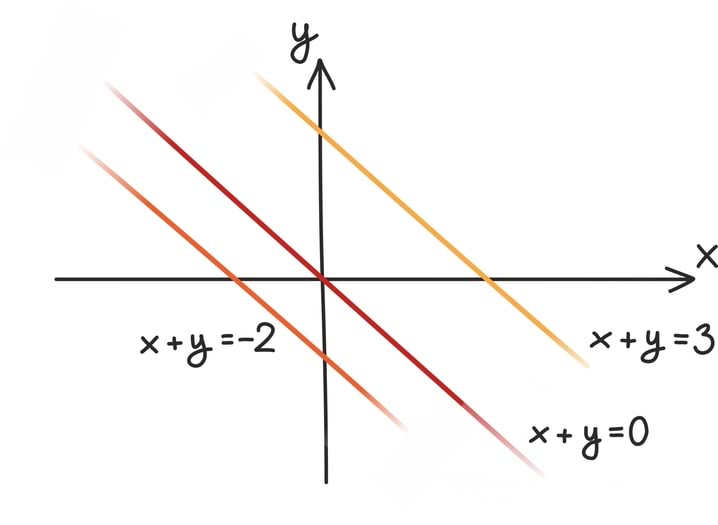
Lähtudes võrrandite keelest võiksime aga küsida: millised sirged vastavad võrranditele kujus x + y = c mingi suvalise arvu c jaoks?

Joonistades võib veenduda, et kõik need sirged on kenasti paralleelsed.

Nii nagu iga kahe muutujaga lineaarne võrrand on täpselt vastavuses mõne tasandi sirgega, on iga kolme muutujaga lineaarne võrrand ilusas vastavuses mõne tasandiga kolmemõõtmelises ruumis.

Ka siin võime geomeetrilisi omadusi kirjeldada võrrandite keeles ja vastupidi. Näiteks võrrandid kujus ax + by + cz = 0 kirjeldavad kõik tasandeid, mis läbivad koordinaatteljestiku nullpunkti. Kõike seda on muidugi juba palju keerulisem joonistada