Ruutfunktsioon ja tema lahendi valem

Ruutfunktsioon või teisisõnu ruutpolünoom on ilmselt koolitunni populaarseim ning käsitletuim funktsioon.

Seda populaarsust saab ka natuke selgitada: ta on väga levinud (mäletate ehk füüsikast läbitud distantsi avaldamist kiirenduse kaudu?), teda on piisavalt lihtne joonistada ning kirja panna ja samas on ruutfunktsiooni nullkohtadel esmapilgul keerulisena näiv lahendivalem, millega õpilasi hirmutada. Või siiski?

Alustame ruutfunktsiooniga tutvumist tema graafiku juurest ja näitame, kuidas kõik erinevad ruutfunktsioonid on lihtsate geomeetriliste teisenduste kaudu omavahel seotud. Seejärel leiame ruutfunktsiooni lahendivalemi ja anname sellelegi geomeetrilise intuitsiooni.

Ruutfunktsiooni graafik

Niipea kui oleme joonistanud ühe funktsiooni graafiku, saame hakata sellega mängima. Näiteks võime seda graafikut nihutada ja erinevatest sirgetest peegeldada.

Kuigi lõbus on see alati, saab sellest protseduurist ka mõnikord kasu lõigata. Näiteks saame nende teisenduste abil meeles pidada trigonomeetriliste teisenduste valemeid [lk 242]. Ruutfunktsiooni korral võime selliste geomeetriliste teisenduste teel luua ühest algfunktsioonist pea kõik teised ruutfunktsioonid ning, nagu hiljem näeme, leida isegi ruutvõrrandi lahendivalemi.

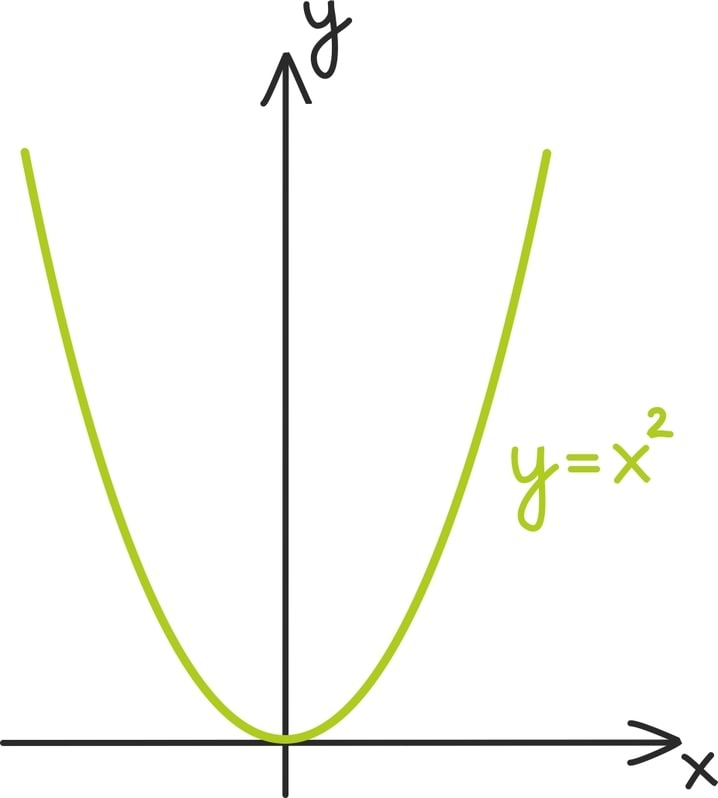
Alustame ruutfunktsioonist

y = f (x) = x^{2}

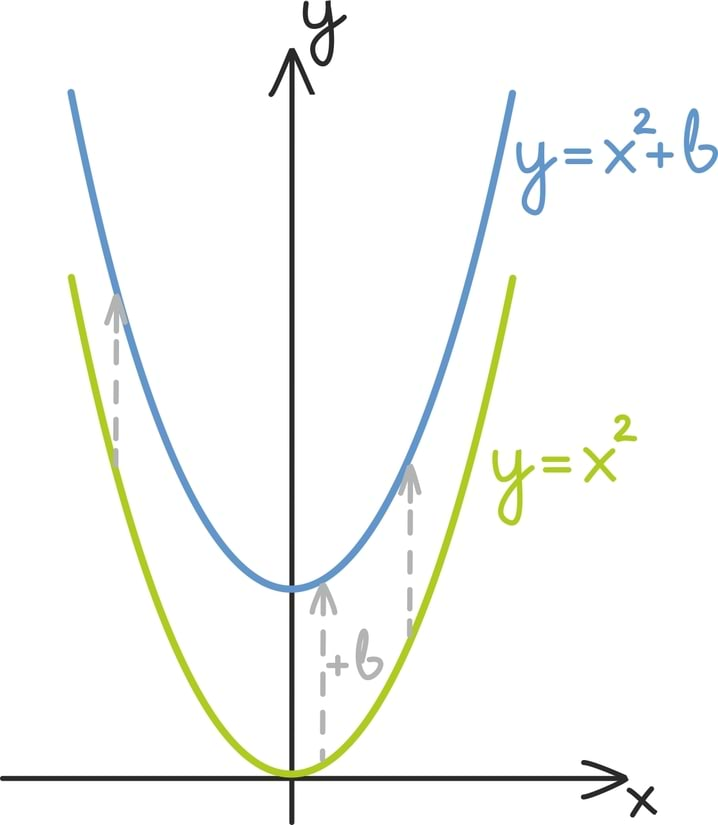
Teda üles-alla nihutades saame funktsioonide kujus

f (x) + b = x^{2} + b

graafikud.

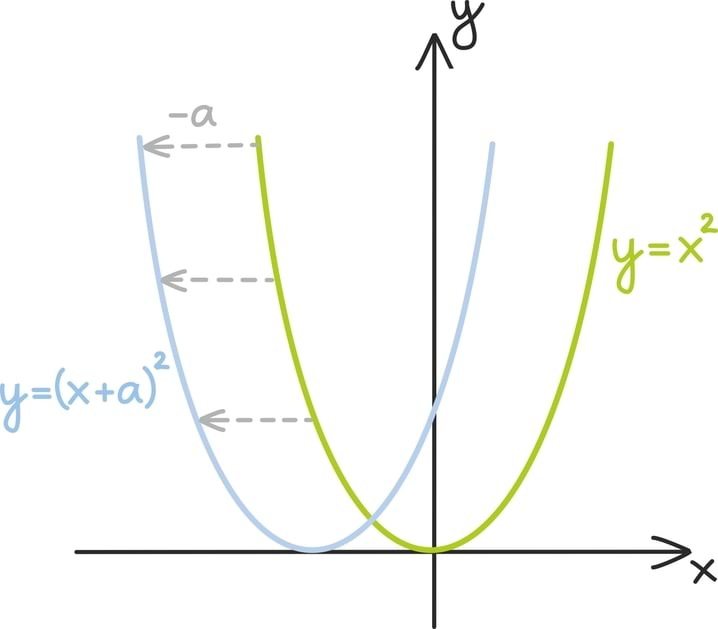
Nihutades algset funktsiooni aga horisontaalselt – või teisisõnu nihutades x-telge tema suhtes –, saame kõik funktsioonid kujus

f (x + a) = {(x + a)}^{2}

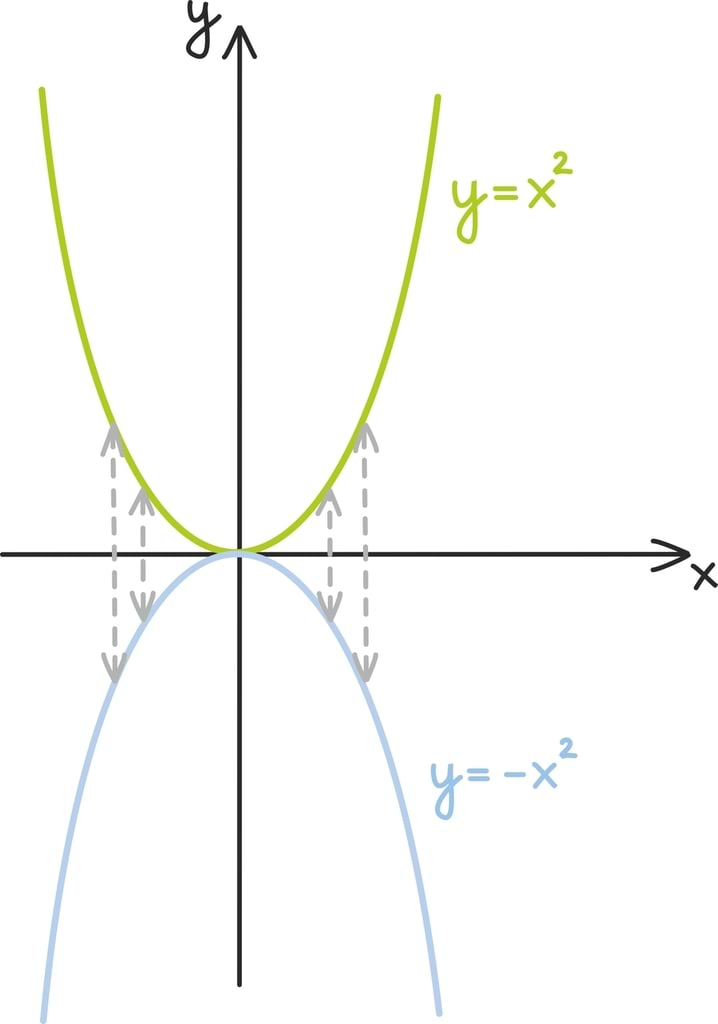
Nüüd, kui peegeldame esialgset funktsiooni x-telje suhtes, saame funktsiooni

- f (x) = {- x}^{2}

graafiku.

Algse funktsiooni peegeldus y-telje suhtes ei tee aga midagi huvitavat – meie funktsioon on y-telje suhtes sümmeetriline ja jääb peegelduse tõttu samaks.

Kõiki neid teisendusi võib muidugi teha ka järjepanu ning nii neid kombineerides leiaksime kõikide funktsioonide kujus

y (x) = \pm x^{2} + a x + b

graafikud. Kui tahaksime päris üldkujusse jõuda, peaksime lisaks veel lubama ka y-telje skaleerimist.

Varsti näeme, et selline geomeetriline mõtlemine annab aimu ka ruutfunktsiooni lahendivalemi tagamaadest. Enne seda lahendame aga ruutvõrrandi puhtalt algebraliselt.

Ruutfunktsiooni lahendivalem

Ruutfunktsiooni lahendivalem võib jääda pisut müstiliseks, kuna tihti ei ole aega seda korralikult tuletada. Tegelikult ei ole selles lahendivalemis midagi hirmsat, kui on viitsimist pisut kaasa mõtelda. Lubame, et ei lähe kauem, kui korraliku suure koorejäätise söömine aega võtaks, ning lubame jäätise ka seltsi võtta. Üritame siis valemi samm-sammult tuletada.

Kõige lihtsam võrrand, mis võib ette tulla, on muidugi x² + c = 0 ehk x² = –c. Sel juhul – kuna ruutjuurt [lk 111] oskame ju hästi võtta – teame, et vastuseks on ±√–c. Oluline on märgata, et miinusmärk c ees ei tähenda sugugi, et meil peaks kohe tegemist olema negatiivse arvuga. Näiteks kui c = –4 saame võrrandi x² – 4 = 0 ning lahenditeks oleksid

\pm \sqrt{- (- 4)} = \pm \sqrt{4}

ehk 2 ja –2.

Raskusi ei valmista ka võrrand a · x2 + c = 0, kuna sel juhul võime lihtsalt kogu võrrandi jagada a-ga läbi ning jõuame sarnaselt eelnevaga vastuseni

\pm \sqrt{\frac{- c}{a}}

Mis aga juhtub, kui juurde tuleb liige b · x ehk kui ruutvõrrand on kujus x2 + bx + c = 0? Tuletame meelde, et võrrandi lahendamine tähendab endiselt, et leiame vastuse kujul

x = m i n g i v a l e m k o r d a j a t e s t

Üldkujus on aga sees ka x-i ruut. Eelnevalt saime temast lahti, rakendades ruutjuurt, ja ausalt öelda, ega mingit muud müstilist trikki ruudust lahti saamiseks pole. Seega tahame ka seekord võtta ruutjuurt. Aga millest?

Ruutjuurt oskame võtta hästi ainult ruutavaldistest. Esimesel juhul oli meil lihtne ruutavaldis x², seekord jõlgub kaasa aga ka libe bx-liige. Kuidas temast lahti saada?

Tuleb lihtsalt märgata, et tegelikult oskame me võtta ruutjuurt mitte ainult x²-st, vaid ka näiteks (x + 4)²-st või (x –1)²-st.

See on abiks, kuna (x + 4)² = x² + 8x + 16 annab meile ka x-iga liikme! Nii saame avaldisest x² + 8x + 16 võtta ilusti ruutjuurt

\sqrt{x^{2} + 8 x + 16} = \sqrt{{(x + 4)}^{2}} = x + 4

Seega tuleb juurimise jaoks leida x-ile sulgudesse õige kaaslane, mis lahtikorrutades annaks liikme bx.

Tuletame meelde, et ruutliikme tegurdamine käib järgnevalt:

{(x + k)}^{2} = x^{2} + 2 k x + k^{2}

Kui nüüd valime

k = \frac{b}{2}

ongi liikme x ees soovitud kordaja b

{(x + \frac{b}{2})}^{2} = x^{2} + b x + \frac{b^{2}}{4}

See näeb välja juba peaaegu nagu meie algne võrrand x² + b · x + c = 0.

Ainsa vahena on ülemises valemis lihtsalt üks üleliigne liige

\frac{b^{2}}{4}

ning liige c on hoopis puudu.

Seega peame algse ruutfunktsiooni kirjeldamiseks lihtsalt ruudust

{(x + \frac{b}{2})}^{2}

maha lahutama üleliigse osa

\frac{b^{2}}{4}

ja tagasi liitma c:

x^{2} + b \cdot x + c = {(x + \frac{b}{2})}^{2} - \frac{b^{2}}{4} + c

Nii saab meie võrrand x² + b · x + c = 0 kuju

{(x + \frac{b}{2})}^{2} - \frac{b^{2}}{4} + c = 0

Viies osa liikmeid teisele poole, oleme juba väga heas positsioonis juurimiseks:

{(x + \frac{b}{2})}^{2} = \frac{b^{2}}{4} - c

Siin saame võtta ruutjuure ning vastuseks tuleb

x + \frac{b}{2} = \pm \sqrt{\frac{b^{2}}{4} - c}

ehk

x_{1, 2} = - \frac{b}{2} \pm \sqrt{\frac{b^{2}}{4} - c}

Taandatud ruutvõrrandi lahendivalem ongi käes!

Kui x² ees on veel kordaja a, peame lihtsalt b ja c läbi jagama a-ga ning jõuame just läbi arutatud olukorrani. Nii on ruutvõrrandi üldkuju ax + bx + x = 0 lahendivalemiks

x_{1, 2} = - \frac{b}{2 a} \pm \sqrt{\frac{b^{2}}{4 a^{2}} - \frac{c}{d}}

mida tihti kirjutatakse ka kujus

x_{1, 2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

Kontrolli, et ka viimane teisendus kehtib!

Selle valemi abil võib lahendada ükskõik millist ruutvõrrandit. Näiteks kui õpetaja lööb lauale ruutvõrrandi x² – 3x – 10 = 0, võime välja võtta oma valemi, sinna sisse pookida a = 1, b = –3 ning c = –10 ning saamegi vastuseks lahendid –2 ja 5.

Lahendivalem geomeetriliselt

Lubasime, et lahendivalemi leidmisest saab ka geomeetriliselt mõelda. Kuna meil on tegelikult juba ruutvõrrandi lahendivalem leitud, siis mingis mõttes on see muidugi tühi töö. Siiski aitab järgnev mõttekäik anda ruutvõrrandi lahendivalemi leidmise erinevatele etappidele ja seega ka lahendivalemile endale geomeetrilist intuitsiooni ning seeläbi ehk aitab valemit ja selle tuletust meeles pidada.

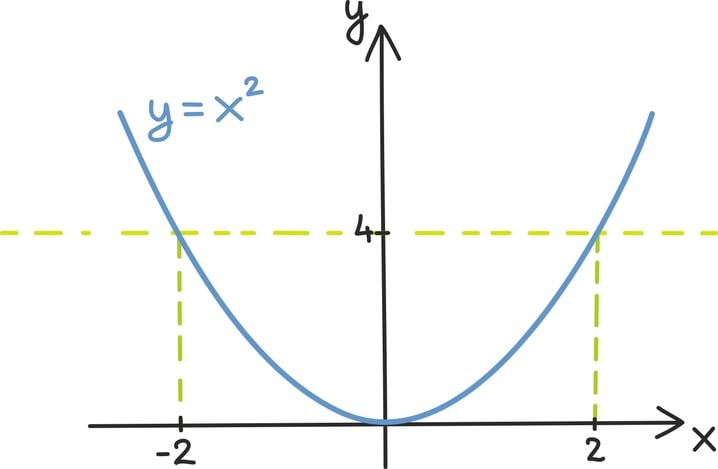
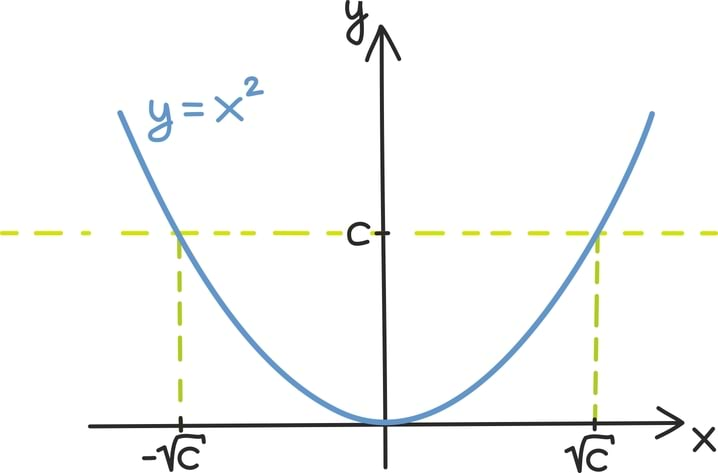
Aluspunktiks on tähelepanek, et ruutvõrrandi x² = c lahendamine tähendab geomeetriliselt täpselt funktsioonide y = x² ning y = c graafikute lõikepunktide x-koordinaatide leidmist. Seda muidugi oskame teha ruutjuurt võttes ja vastuseks on

x_{1, 2} = \pm \sqrt{c}

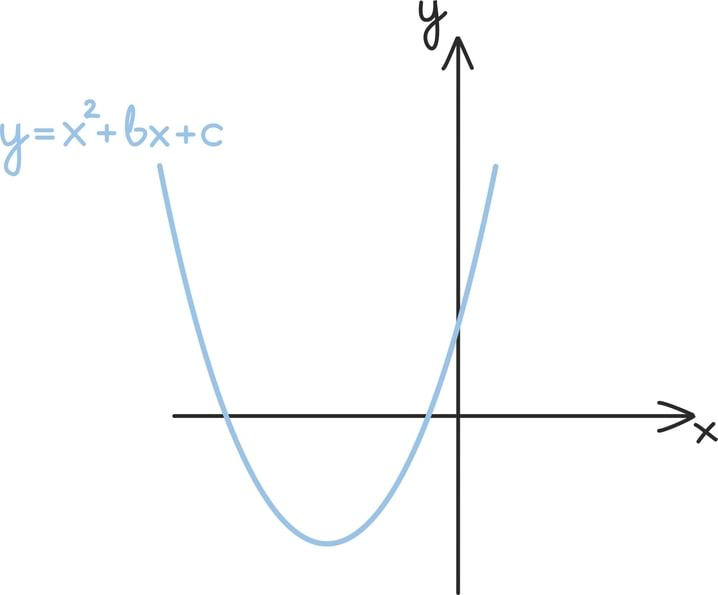
Peaaegu üldkujus ruutvõrrandi x² + bx + c = 0 lahendamine tähendab omakorda muidugi ruutfunktsiooni y = x² + bx + c ning x-telje lõikepunktide leidmist.

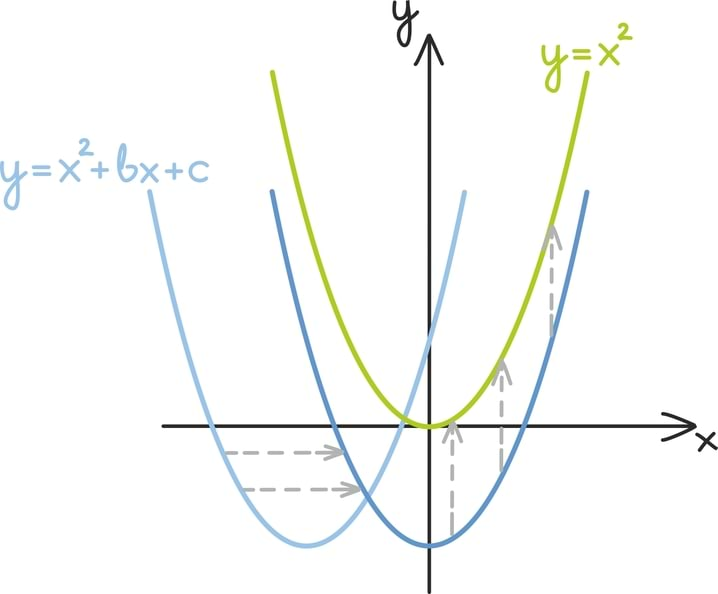
Kogu ruutfunktsiooni lahendivalemi leidmiseks vaja läinud teisendusterea eesmärk oli taandada teine olukord esimesele, taandada keerulisemate lõikepunktide leidmine lihtsamate lõikepunktide leidmisele. Mingis mõttes tähendab see, et tahame oma suvalise ruutfunktsiooni graafiku teisendada ruutfunktsiooni y = x² graafikuks.

Selle jaoks nihutame esmalt funktsiooni graafikut

\frac{b}{2}

võrra horisontaalselt (positiivne suund on paremale), et funktsiooni graafik oleks sümmeetriline y-telje suhtes.

Seejärel liigutame graafikut

\frac{b^{2}}{4} - c

võrra vertikaalselt (positiivne suund on üles), et viia graafiku kõige alumine punkt täpselt koordinaatteljestiku nullpunkti.

Nii oleme kahe teisenduse abil jõudnud funktsiooni y = x² graafikuni.

Kuidas on teisenenud algse ruutvõrrandi nullkohad? Kui enne olid nad sirge y = 0 ning algse ruutfunktsiooni lõikepunktid, siis teisenduste käigus esiteks nihutasime neid lõikepunkte

\frac{b}{2}

võrra horisontaalselt ning seejärel tõstsime

\frac{b^{2}}{4} - c

võrra.

Nende teisenduste järel said nullkohtadest funktsiooni y = x² ning sirge

y = \frac{b^{2}}{4} - c

lõikepunktid.

Nende lõikepunktide x-koordinaadid on aga täpselt antud valemiga

\pm \sqrt{\frac{b^{2}}{4} - c}

Kuna vertikaalsed, üles-alla teisendused x-koordinaate ei muuda, peame ainult arvesse võtma veel horisontaalse nihke. Uued lõikepunktid on algsete suhtes

\frac{b}{2}

võrra nihutatud, seega peame algsete lõikepunktide x-koordinaatide leidmiseks lahutama veel

\frac{b}{2}

Saamegi taas kord loodetud vastuse.

x_{1, 2} = \pm \sqrt{\frac{b^{2}}{4} - c} - \frac{b}{2}

Seekord on aga mõlemal liikmel ka taust: esimene tuleb funktsiooni sellisest üles-alla nihutamisest, et ta istuks täpselt horisontaalteljel. Teine pärineb horisontaalsest nihutamisest, mis viib funktsiooni graafiku sümmeetriliseks vertikaaltelje suhtes.