Logaritmid on ajalooliselt panustanud tublisti ka loodusteaduste ja eriti just astronoomia arengusse: nad võimaldasid juba enne arvutite leiutamist inimestel korrutada suuri ja keerulisi arve.
Logaritmide abi oli nii määrav, et uhke astronoom ja matemaatik Laplace oli omal ajal logaritmidest lausa joovastuses: „Imetlusväärne nõks, mis taandab mitme kuu töö vaid mõnele päevale, kahekordistades nõnda astronoomi elu ja hoides teda pikkade arvutustega kaasnevatest vigadest ja tülgastusest.” Kust see kõik tuleb?
Kõige motiveerivam on ilmselt veidi peast arvutada: 7323118 · 919222!
Õudus! Mida küll teha sellise tehtega? Tänapäeval on muidugi väga lihtne: võtad pinginaabri kotist taskuarvuti või nutitelefoni ja arvutus saab pärast mitut ebaõnnestunud katset siiski tehtud. Võib ka pikalt ja kirjalikult korrutama hakata, aga see võtab mõistuspäratult aega ja pole ei põnev ega lõbus.
17. sajandil ei olnud astronoomidel veel taskuarvuteid, kuid nende arusaam lõbust polnud sugugi nii palju erinev: neilegi ei meeldinud pikki ja igavaid arvutusi teha. Ometigi oli taevakehade liikumises tihti vaja korrutada suuri ja kosmiliselt suuri arve. Appi tuli logaritm.
Kuidas logaritm siis arvutusi lihtsustas?
Logaritmi idee arvutuste lihtsustamisel peitub tema kuulsas omaduses teha korrutamisest liitmine: log(ab) = log(a) + log(b).
Nii taandame korrutamise liitmisele ja liita on ju määratult lihtsam.
Kuidas siis näiteks korrutada omavahel 7323118 ja 919222?
Võtame kõigepealt mõlemast arvust logaritmid alusel 10, seejärel liidame need logaritmid kokku ning kasutame tulemust 10 astendamisel:
Kaks esimest tehet on muidugi võimalikud, kuna logaritmfunktsioon on igal alusel määratud kõikide positiivsete reaalarvude korral.
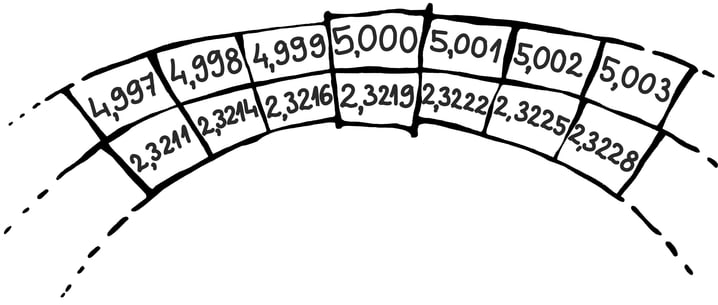
Tulemuse saamiseks piisaks nüüd ühest suurest tabelist. Esiteks peaks sealt saama piisava täpsusega järele vaadata arvude logaritme ehk kuidas neid esitada kümne astmena – näiteks 7323118 juures oleks kirjas 6,864 ning 919222 juures 5,963. Teiseks peaks sealt leidma ka vastupidist teavet: iga arvu x jaoks astme 10x väärtuse – näiteks 5,001 koha peal oleks kirjas 10023. Muidugi ei saaks tabelis olla lõpmatult palju arve ja seega peaksid kõik arvud tabelis olema antud mingi teatava täpsusega, näiteks kolme või nelja komakohaga.
Nii võiksime oma arvutuse teha väga kiirelt. Alustuseks leiaksime tabelist arvud 6,864 ja 5,963, siis liidaksime nad, et saada 12,827, ning viimaks vaataksime tabelist järele arvu 1012,827 väärtuse: 6 714 000 000 000. Kuna päris vastus on 6 731 571 174 196, näeme, et meie täpsus on nõnda üsna talutav.
Muidugi pidid logaritmitabelid olema kavalalt kokku pandud, et sinna mahutada võimalikult palju arve. Võid ise näha, kui pikaks läheks tabel, kui lihtsalt laduda ühte ritta arvud ja teise nende logaritmid:
Ülemisel real oleme edasi liikunud seitsme lahtriga ainult 0,006 võrra! Joonisel asuv tabel on küll tõesti avatud hoopis teiselt kohalt ja on ka hoopis teisel alusel, aga see suurt ei muuda. Muuseas, võibolla nuputad välja, mis aluse jaoks see tabel on?
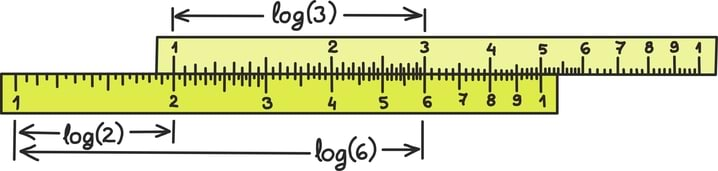
Siiski on ka suurtest arvutabelitest vaatlemine ja ise kokku liitmine tüütu ning peatselt peale logaritmi leiutamist tuldi lagedale veel kavalama idee ja riistapuuga. Selle nimeks on lükati ja teda kasutati veel 20. sajandi keskpaigaski, niikaua kui taskuarvutid ta välja puksisid.
Korrutamist lihtsustaval lükatil on arvud paigutatud kavalalt, logaritmskaalalisel kaugusel ja nii võib korrutamistehtega ühele poole saada lihtsalt lükati ülemist hooba alumise suhtes liigutades. Näiteks antud joonisel on omavahel korrutatud 2 ja 3. Suure täpsuse jaoks joonistati skaaladki ülitäpsed. Räägitakse, et observatooriumites kasutati tähtsamateks arvutusteks mitmemeetriseid lükateid ning skaalasid uuriti samal ajal mikroskoobiga.