Piirväärtus ja pidevus

Piirväärtustest räägitakse kooliprogrammis eelkõige jadade ja funktsioonide puhul.

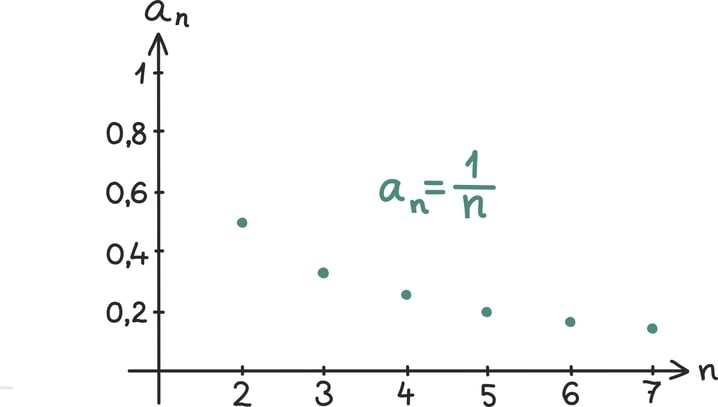
Näiteks jada

a_{n} = \frac{1}{n}

liikmed muutuvad järjest väiksemaks ja lähenevad hoogsalt nullile. Tõepoolest:

\begin{matrix} a_{1} = \frac{1}{1} = 1, a_{2} = \frac{1}{2} = 0, 5, a_{3} = \frac{1}{3} = 0.3 ¯ 3, a_{4} = \frac{1}{4} = 0, 25, \dots \end{matrix}

Sellisel juhul tundub mõistlik rääkida ka sellest, mis juhtub siis, kui jada liikmed otsa lõpevad. Mingis mõttes tahame rääkida jada „lõpmatult kaugest” liikmest. Tema väärtus konkreetsel juhul peakski olema null.

Jada piirväärtuse mõiste annab sellisele „lõpmatu kaugele” liikmele täpse tähenduse, aitab kindlaks teha, millal ta eksisteerib, ning leida tema väärtuse.

Ka funktsioonide korral võime rääkida väärtustest, mis jäävad lõpmatult kaugele – näiteks funktsiooni

f (x) = \frac{1}{x}

piirväärtus, minnes lõpmatult kaugele, on analoogselt jada näitega null.

Funktsioonide korral on piirväärtustel siiski ka teine, ilustav roll.

Vaatame näiteks funktsiooni

f (x) = \frac{x^{2} - 1}{x - 1}

Kui x on ühest erinev, võime nimetaja ja lugeja x – 1-ga läbi jagada. Saame, et iga ühest erineva arvu korral on meie funktsioon võrdne sirgega ƒ(x) = x + 1. Kohal 1 me funktsiooni väärtust aga välja arvutada ei tohi – nulliga ju jagada ei saa.

Ometigi, joonistades funktsiooni

f (x) = \frac{x^{2} - 1}{x - 1}

graafiku kõikide ühest erinevate argumendi x väärtuste jaoks, näeme, et valides argumendi väärtuseid järjest lähemal ühele, läheneb ƒ(x) väärtus ühtlaselt kahele.

Näiteks

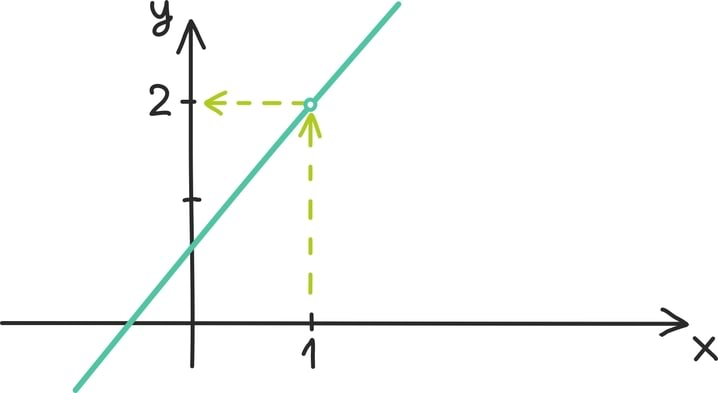
\begin{matrix} f (1, 2) = 2, 2, f (1, 05) = 2, 05, f (1, 0001) = 2, 001, f (1, 0000001) = 2, 0000001 \end{matrix}

Seda demonstreerib ka kenasti funktsiooni graafik:

Nii tundub, et funktsiooni

f (x) = \frac{x^{2} - 1}{x - 1}

loomulik väärtus kohal üks peaks olema täpselt kaks.

Piirväärtus annabki funktsioonide korral sellisele loomulikule augutäitmisele täpse tähenduse.

Kokkuvõttes võib öelda, et piirprotsessid aitavad meil aru saada ja kindlaks määrata, mis juhtub seal, kuhu meil pole lubatud vaadata või kuhu me ei ulatu vaatama.