Sõna kiirus on kõigile tuttav, nõndasama kui tema matemaatiline definitsioon:

Selleks et käsitleda esemeid, mille kiirus muutub, nõnda kui Galilei langevatel kehadel, peame ülaltoodud definitsiooni täpsustama, nimetades määratletud suurust keskmiseks kiiruseks.[*[Keskmise kiiruse algebraline avaldis on

Kriips $v$ kohal tähistab keskväärtust, $\Delta x$ on ajavahemikus $\Delta t$ läbitud teepikkus.

]*] Kiirust igal hetkel saab mõõta, valides küllalt lühikese ajavahemiku vaatlusaluse hetke ligidal. Isaac Newtoni kõrgem matemaatika  on viis asjade kirjeldamiseks, kujutledes infinitesimaalseid (kaduvväikesi) vahemikke. Kuid meil pole tarvis nii kaugele minna. Meile piisavaid lihtsamaid juhte saab näitlikustada graafikute abil, mis kujutavad teepikkuse sõltuvust ajast.

Joonis 1-1 Ühtlase liikumise graafikud.	Joonis 1-2 Ühtlaselt kiireneva liikumise graafik.

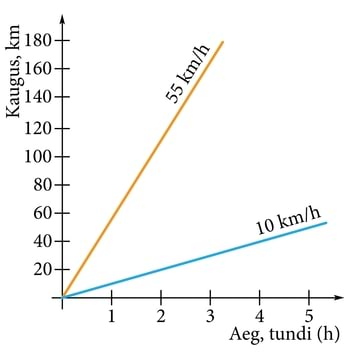
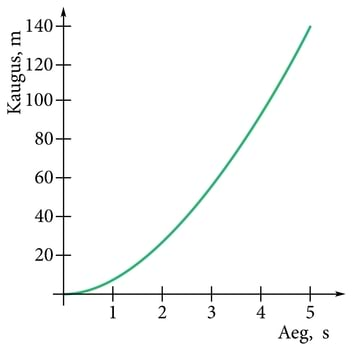
Kui miski liigub jääva kiirusega, on graafikuks sirgjoon, nagu joonise 1-1 kahes näites. Mida järsemalt see joon tõuseb, seda suurem on kiirus. Kui kiirus muutub, peab muutuma ka joone tõusunurk. Sel juhul saame kõverjoone, nagu joonisel 1-2. Nähes niisugust graafikut, taipame, et tegemist on kiireneva liikumisega.

Argikõnes tähendab kiirendus üksnes kiiruse kasvu. Füüsiku keelepruugis võib ta tähendada ka aeglustumist. Sel juhul on kiirendus negatiivne. Kolmandas peatükis näeme, kuidas seda definitsiooni veelgi üldistatakse, nii et ta peaaegu kaotab seose kiirenduse üldkäibiva tähendusega. Kalduvus laenata sõnu tavakeelest ja siis teisendada nende tähendust nõnda, et see vastaks matemaatilisele definitsioonile, on üks neid asju, mis hämmeldab füüsikaga tutvumisel.

Kiirenduse matemaatilise määratluse annab valem

Näiteks kui auto kiirus kasvab $5$ sekundi jooksul nullist $45$ kilomeetrini tunnis, siis ta on saanud kiirenduse $45/5=9$ kilomeetrit tunnis sekundi kohta.

Kui lubame kiirendusel omandada ka negatiivseid väärtusi, kirjeldab ta samahästi ka liikumise aeglustumist. Näiteks kui auto aeglustab $6$ sekundiga sõitu $50$st kilomeetrist tunnis $20$ kilomeetrini tunnis, siis on kiiruse muutus $20-50=-30$ kilomeetrit tunnis, seega kiirendus tuleb $a=-30/6=-5$ kilomeetrit tunnis sekundi kohta. Nendes näidetes oleme meelega valinud erinevad ajaühikud kiiruse (tunnid) ja kiirenduse (sekundid) kirjeldamiseks. Füüsikud kasutavad tavaliselt mõlemile samu ühikuid. Nende lemmik-mõõdusüsteemis, SI-süsteemis teeb $9km$ tunnis sekundi kohta $2,5$ meetrit sekundis sekundi kohta, mida siis lühidalt öeldakse "meetrit ruutsekundi kohta", lühendatult $m/s^2$. Termin võib segadusse ajada – misasi küll võiks olla "ruutsekund"? Vastuseks on, et ruut tähendab siin lihtsalt seda, et kui tahate kauguste mõõtmiselt jõuda kiirenduste võrdlemiseni, peate ajaga lihtsalt kaks korda läbi jagama.

Mõistnuks Galilei lugejad seda keelt, võinuks ta tihendada oma keha langemiskirjelduse üheksainsaks lühilauseks:

Liikumistakistuse puudumisel saavad kõik langevad kehad ühesuguse püsiva kiirenduse.

Kui auto meie näites suurendaks kiirust samal moel, jõuaks ta ühe sekundi pärast $9$ kilomeetrini tunnis, teise sekundi lõpul oleks see $18km/tunnis$, ja kümnenda sekundi järel $90km/t$. Samaviisi, kui ta aeglustuks ühtlaselt $-5km$ tunnis sekundi jooksul, kuluks tal kümme sekundit, et $50$-kilomeetriselt tunnikiiruselt peatuda.

Kuid Galilei päevil ei olnud seadmeid ei kiiruse ega kiirenduse otseseks mõõtmiseks. Siin tuleb mängu matemaatika teinegi roll. Galilei seadus oli sõnastatud millegi otseselt mõõdetamatu kaudu. Kuid matemaatiliselt sai neist tuletada väited asjade kohta, mida sai mõõta. Lihtsa algebra abil sai Galilei teisendada oma väite konstantsest kiirendusest suhteks mõõdetavate suuruste, teepikkuse ja aja vahel.

Tema tuletatud seos käis paigalseisust ühtlaselt kiireneva keha kohta, teepikkus kasvab selle järgi võrdeliselt aja ruuduga.[*[Algebraliselt väljendub see seadus kujul $x=\frac{1}{2}a{t}^2$, kus $x$ tähistab teepikkust, $a$ kiirendust ja $t$ aega. Tegur $1/2$ tuleb sisse seepärast, et kui keha saab kiirenduse paigalseisust, siis tema keskmine kiirus võrdub poolega lõppkiirusest.]*]

Näiteks paigalt poetatud keha langeb esimese sekundiga umbes $5$ meetrit. Kahe sekundiga langeb ta neli ($2^2$) korda enam, so $20$ meetrit, kolme sekundiga $5\times 3^2=45$ meetrit jne.

Põhjus, miks aeg tuleb ruutu võtta, on silmnähtav. Et saada kiirendusest kiirust, tuleb see ajaga korrutada. Et kiiruse järgi arvutada läbitud teed, tuleb veel kord korrutada ajaga, nii saamegi aja ruudus.

Mõõdetavate suurusteni jõudmine ei lõpetanud veel Galilei kimbatusi. Vaevalt suutnuks ta mõõta sekundi murdosi isegi parimate tolleaegsete ajamõõturitega. Kuid  isegi kõrgeimatest tornidest, kuhu ta võis jõuda, oleks raske ese maapinnani langenud ainult pisut rohkem kui $3$ sekundit. Ta pidi leidma viisi, kuidas aega "välja venitada".

Selleks otsustas Galilei loobuda vabalt langevate kehade uurimisest. Selle asemel tegi ta mõõtmisi kaldpinda mööda alla veereva keraga. Ta väitis (kuigi ei suutnud seda tõestada), et see "lahjendab" liikumist (so kahandab kiirendust), kuid ei muuda oluliselt liikumise loomust.

Kasutades väikese kaldega tasast lauda, mille keskel oli renn kera suunamiseks, sai Galilei uurida liikumist, mis võttis aega kümne sekundi ümber. Ajamõõturiks oli tal veepott, mille põhja tehtud prundiga suletav auk. Kera lasti veerema eri kohtadest piki lauda. Kuuli veeremise ajaks tõmmati prunt eest ja vesi voolas topsi augu all. Pärast kaaluti veetops ära, ja selle kaal võeti aja mõõduks. Vee kaalu ruut osutus võrdeliseks veeremistee pikkusega. Galilei ennustus osutus tõeks.

Galilei meetodi olemus seisnes lühidalt järgnevas. Tuleb alustada idealiseeritud kirjeldusega, mis võib olla väljendatud ka mittemõõdetavate suuruste kaudu. Edasi tuleb see kirjeldus  matemaatiliselt teisendada väideteks mõõdetavate suuruste kohta. Kui looduses on jälgimiseks liig kiireid liikumisi, siis aeglusta neid niiviisi, et see ei muudaks midagi olulist. Selles on kauge kaja aristotellikust õpetlasest, kes võtab loodust nii nagu see tema ees on, vaatleb hoolikalt ja kannab nähtu oma märkmikku.

Kuid see ei olnud ka puhas platonism. Inimpõlv enne Galileid oli juba tehtud katset mõista vaba langemist umbes samamoodi. Seda tegi ei keegi muu kui täiuslikem renessanslane, Leonardo da Vinci. Otsides lihtsat matemaatilist seaduspära, arvas Leonardo, et järjestikustel sekunditel läbitud distantsid järgivad naturaalarvude jada, s.o. $1,2,3,4,\dots$ See oli selge numbrikultus, mis osutus eksituseks.

Mis oli Galilei eelisteks Leonardo ees? Üks neist oli muidugi tema  matemaatikuharidus. Kuid küllap veelgi olulisem oli see, et ta teadis juba ette  teepikkuse ja aja õiget vahekorda, mille andis katse. Järgmisest peatükist loeme, et ühtlase kiirenemise põhimõte ei olnud tema lähtepunkt, vaid järeldus pikast uuringute ahelast.