Ujumine risti üle jõevoolu ja tagasi võtab vähem aega kui sama distantsi katmine otse üles-ja allavoolu. Michelsoni katse oli rajatud sellele tõdemusele. Selle seiga matemaatiline tõestus pole iseendast teab kui oluline, kuid tema tulemuseks on avaldis, mis on Einsteini relatiivsusteooria nurgakiviks. Seepärast teeme ta siin läbi. Tulemus on siin tähtsam kui tuletuskäik ise.
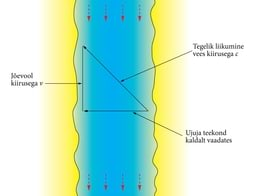
Kujutleme, et ujuja tahab pääseda risti üle jõe vastaskaldal asuvasse punkti. Ta ujub kiirusega c ja jõgi voolab kiirusega v. Et voolu kompenseerida, peab ujuja suunduma mõnevõrra ülesvoolu. Kaldalseisjale paistab, et ujuja läheb otse ülejõe, kuid kui keegi vaatab teda voolust kantud paadist, näib teekond olevat jõe suhtes kaldu, piki joonisel 8-3 näidatud kolmnurga hüpotenuusi.
Et leida, kui palju lisateed peab ujuja läbima, võrdleme hüpotenuusi kolmnurga alusega, milleks on jõe laius. Hüpotenuus annab ujuja teekonna vees kiirusel c. Kolmnurga allavoolu-külg annab vahemiku, mille sama aja jooksul katab vool kiirusel v. Pythagorase teoreemi järgi onhüpotenuusi ruut võrdne kaatetite ruutude summaga. Kuna meie teame hüpotenuusi c ja üht kaatetit v, leiame, et kaldalt mõõdetuna peab ujuja kiirus olema
Relatiivsusteoorias tuntakse ujuja tegeliku kiiruse ja kaldalt näiva knruse suhet Lorentzi faktori nime all ja seda tähistatakse tihti kreeka tähega γ:
Joonis 8-4 näitab, kuidas γ sõltub kiiruste suhtest v/c. Toome arvulise näite. Olgu ujuja kiirus 5 km/h ja voolu kiirus 3 km/h. Siis on v/c=0,3 selle ruut 0,36 ja
Ruutjuur 0,64 on 0,8, seega γ = 1,25. Järelikult peab ujuja vees katma 25% pikema maa, kui on jõe laius.
Kui vesi ei voolaks, oleks v = 0 ja γ = 1, sest siis peaks ujuja ületama ainult veekogu laiuse. Sellest väiksemat väärtust ei saa y omandada, ta võib olla vaid 1,0 või sellest suurem. Siit järeldub, et jõe ületamisel on vool alati takistuseks, mitte abiks.
Tähtsaim on see, et valem pole rakendatav, kui v on suurem kui c, sest me ei saa võtta ruutjuurt negatiivsest arvust. Siis voolab jõgi ujujast kiiremini ja pole mingit võimalust üle jõuda. Relatiivsusteoorias saab see piirang veelgi sügavama tähenduse.
Me ei hakka arvutama päri- ja vastuvoolu ujumise juhte, siin on arvutus mõneti keerukam. Vastuvoolu jõuab ujuja edasi kiirusega c – v ja pärivoolu c + v. Vastuvoolu ujumiseks läheb rohkem aega, nii et keskmine kiirus edasi-tagasi teekonnal tuleb väiksem kui c. Algebras kodusemad lugejad võiksid kontrollida, et keskmiste kiiruste suhe tuleb siin γ2.
Valguse kiirusest palju väiksemate kiiruste jaoks kehtib Lorentzi faktori ligikaudne valem:
See valem kõlbab ainult siis, kui v on väiksem kui 1/100 valguse kiirust.