Ideaalse gaasi siseenergia ja soojusmahtuvus

Et ideaalses gaasis puuduvad sõltumata osakestevahelisest kaugusest igasugused jõud molekulide vahel, siis on ideaalse gaasi siseenergia tema üksikute molekulide energiate summa. Järelikult on ühe kilomooli idealse gaasi energia võrdne Avogadro arvu ja ühe molekuli keskmise energia korrutisega:

(102.1)

U_{k m} = N_{A} ¯ ¯ ¯ ε = \frac{i}{2} N_{A} k T = \frac{i}{2} R T

Suvalise gaasihulga massiga $m$ siseenergia on võrdne ühe kilomooli gaasi energia ja selles gaasihulgas sisalduvate kilomoolide arvu korrutisega:

(102.2)

U = \frac{m}{μ} U_{k m} = \frac{m}{μ} \frac{i}{2} R T

Keha soojusmahtuvuseks nimetatakse suurust, mis võrdub soojushulgaga, mille peame kehale andma, et tõsta tema temperatuuri ühe kraadi võrra.

Kui kehale antud soojushulga $d^{'} Q$ arvel keha temperatuur tõuseb $d T$ võrra, siis definitsiooni kohaselt on selle keha soojusmahtuvus

(102.3)

C_{k e h a} = \frac{d Q^{'}}{d T}

Suuruse (102.3) dimensioon on $J / K$ .

Tähistame kilomooli aine soojusmahtuvust tähega $C$ . Selle suuruse dimensioon on $J / (k m o l \cdot K$ ).

Massiühiku aine soojusmahtuvust nimetatakse erisoojuseks ja tähistatakse tähega $c$ . Erisoojuse dimensioon on $J / (k g \cdot K$ ).

Kilomooli aine soojusmahtuvuse ja sama aine erisoojuse vahel valitseb seos

(102.4)

c = \frac{C}{μ}

Soojusmahtuvuse väärtus sõltub keha soojendamise tingimustest. Suurimat huvi pakuvad juhud, kus keha soojendatakse kas jääval ruumalal või jääval rõhul. Esimesel juhul on tegemist soojusmahtuvusega jääval ruumalal (tähistus $C_{V}$ ), teisel soojusmahtuvusega jääval rõhul ( $C_{p}$ ).

Kui keha soojendada jääval ruumalal, siis ei tee ta tööd ning järelikult läheb kogu soojus termodünaamilika esimese printsiibi kohaselt (vt. (95.4)) keha siseenergia juurdekasvuks

(102.5)

d^{'} Q_{V} = d U

Seosest (102.5) järeldub, et iga keha soojusmahtuvus jääval ruumalal

(102.6)

C_{V} = \frac{d U}{d T}

Seega peame kilomooli ideaalse gaasi soojusmahtuvuse määramiseks jääval ruumalal diferentseerima tema siseenergia avaldist (102.1) temperatuuri järgi. Saame:

(102.7)

C_{V} = \frac{i}{2} R

Nagu viimasest avaldisest näha, on ideaalse gaasi soojusmahtuvus jääval ruumalal konstantne suurus, mis ei sõltu gaasi olekuparameetritest ega temperatuurist.

Arvestades valemit (102.7), võime ideaalse gaasi siseenergia valemi kirjutada uuel kujul:

(102.8)

U_{k m} = C_{V} T

Kui gaasi jääval rõhul soojendada, siis gaas paisub, tehes positiivset tööd. Järelikult on sel juhul gaasi temperatuuri tõstmiseks ühe kraadi võrra tarvis rohkem soojust, kui soojendamisel jääva ruumala korral: osa soojust kulub gaasi paisumistööks. Seega peab soojusmahtuvus jääval rõhul olema suurem, kui soojusmahtuuvs jääval ruumalal.

Kirjutame termodünaamika esimese printsiibi võrrandi (96.4) kilomooli gaasi kohta

(102.9)

d^{'} Q_{p} = d U_{k m} + p d V_{k m}

Selles avaldises märgib indeks p seda, et gaasile antakse soojust jääval rõhul $p$ . Jaganud võrrandi (102.9) $d T$ -ga, saame kilomooli gaasi soojusmahtuvuse jääval rõhul:

(102.10)

C_{p} = \frac{d U_{k m}}{d T} + p (\frac{d V_{k m}}{d T})_{p}

Nagu nägime, on $\frac{d U_{k m}}{d T}$ kilomooli soojusmahtuvus jääval ruumalal. Seega võime valemi (102.10) kirjutada kujul

(102.11)

C_{p} = C_{V} + p (\frac{d V_{k m}}{d T})_{p}

Suurus ${(\frac{d V_{k m}}{d T})}_{p}$ on kiulomooli ruumala juurdekasv temperatuuri tõusul ühe kraadi võrra jääval rõhul. Olekuvõrrandi (98.13) kohaselt

V_{k m} = \frac{R T}{p}

Diferentseerinud seda avaldist $T$ järgi ( $p = const$ ), leiame

(\frac{d V_{k m}}{d T})_{p} = \frac{R}{p}

Teinud viimase avaldise alusel asenduse võrrandis (102.11) saame

(102.12)

C_{p} = C_{V} + R

Seega on töö, mida teeb üks kilomool gaasi soojendemisel ühe kraadi võrra jääval ruumalal, võrdne universaalse gaasikonstandiga.

Peame silmas, et avaldis (102.12) on saadud ideaalse gaasi olekuvõrrandit kasutades, seega kehtib ta ka ainult ideaalse gaasi puhul.

Arvestades valemit (102.7) saame $C_{p}$ arvutamiseks järgmise avaldise:

(102.13)

C_{p} = \frac{i}{2} R + R = \frac{i + 2}{i} R

Jagades valemi (102.13) valemiga (102.7) saame igale gaasile iseloomuliku sute $C_{p} / C_{V}$ :

(102.14)

γ = \frac{C_{p}}{C_{V}} = \frac{i + 2}{i}

Nagu näha valemist (102.14) on suurus $γ$ määratud molekulide vabadusastmete arvu ja iseloomuga.

Tabelis 4 on toodud $C_{V}$ , $C_{p}$ ja $γ$ väärtused eri molekulide jaoks, arvutatuna valemite (102.7), (102.13) ja (102.14) abil.

Tabelis 5 kõrvutatakse teooriatulemusi eksperimendiandmetega. Teoreetilised väärtused(välaj arvatud üks eraldi märgitud juht) on saadud eeldusel, et molekulid on jäigad; eksperimendiandmed on saadud toatemperatuurile lähedastel temperatuuridel.

Tabeli 5 pealiskaudsel silmitsemisel paistab kooskõla teooria ja eksperimendi vahel, vähemalt ühe- ja kaheaatomiliste gaaside teooria puhul, täiesti rahuldav olevat. Tegelikult pole asi nii. Vaadeldud teooria järigi peavad gaaside soojusmahtuvused olema suuruse R/2 täisarvkordsed, sest vabadusastmeid saab olla ainult täisarv. Seepärast mängivad suuruste $C_{V}$ ja $C_{p}$ väärtuste väiksedki kõrvalekaldumised $R / 2$ täisarvkordsetest põhimõttelist osa. Kuid nagu tabelist näha, leiavad niisugused, ilmselt võimalike katsevigade piiri ületavad kõrvalekaldumised aset.

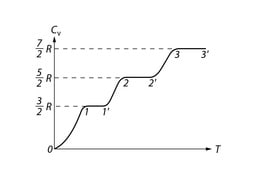
Eriti silmatorkav on erinevus teooria ja eksperimendi vahel siis, kui uurida soojusmahtuvuse temperatuurisõltuvust. Joonisel 233 on kujutatud kilomooli vesiniku soojusmahtuvuse $C_{V}$ sõltuvus temperatuurist katseandmetel. Teoreetiliselt ei tohiks soojusmahtuvus sõltuda temperatuurist (vt. (102.7)). Nagu jooniselt näha, on see nii vaid üksikute temperatuuriintervallide ulatuses, kusjuures eri intervallidele omased soojusmahtuvuse väärtused vastavad molekuli erinevale vabadusastmete arvule. Näiteks piirkonnas 1-1' $C_{V} = \frac{3}{2} R$ . See tähendab, et molekul käitub nagu süsteem, millel on ainult kulgliikumise vabadusastmed. Piirkonnas 2-2' on $C_{V} = \frac{5}{2} R$ . Järelikult sellele piirkonnale vastavatel temperatuuridel tekib molekulil lisaks madalamatel temperatuuridel ilmnevale kolmele kulgliikumise vabadusastmele veel kaks pöörlemise vabadusastet. Lõpuks, küllalt kõrgetel temperatuuridel saab $C_{V}$ võrdseks $\frac{7}{2} R$ , mis annab tunnistust molekuli temperatuurivõnkumistest. Nimetatud intervallide vahel kasvab soojusmahtuvus temperatuuri tõusuga monotoonselt, mis nagu tähendaks kilomooli soojusmahtuvuse vastavust mittetäisarvulisele muutlikule vabadusastmete arvule.

Seega sõltub soojusmahtuvuses avalduv molekuli vabadusastmete arv temperatuurist. Madalatel temperatuuridel ilmneb ainult molekulide kulgliikumine, kõrgematel tekib lisaks ka molekulide pöörlemine. Veel kõrgematel temperatuuridel liitub esimese kahe liikumisega molekulide võnkumine. Peale selle näitab soojusmahtuvuse monoonne muutumine, et pöörlemisse ega võnkumisse ei tõmmata kõiki molekule korraga. Esialgu hakkab näiteks pöödlema väike osa molekulidest. Temperatuuri tõustes see osa suureneb ning lõpuks temperatuuri teatud väärtusel no pöörlemisest haaratud praktiliselt kõik molekulid. Analoogiline protsess leiab aset ka molekulide võnkumiste puhul.

Niisugust soojusmahtuvuse käitumist seletab kvantmehaanika. Kvantteooria järgi on molekulide pöörlemise ja võnkumise enrgia kvanditud. See tähendab, et ei oöörlemise ega võnkumise energia saa omada suvalisi, vaid ainult diskreetseid, s.o. ükskuid omavahel lülliku suuruse võrra erinevaid väärtusi. Järelikult võib nende liikumise liikidega seotud energia muutuda ainult astmeliselt. Kulgliikumise energia kohta niisugust keeldu ei ole.

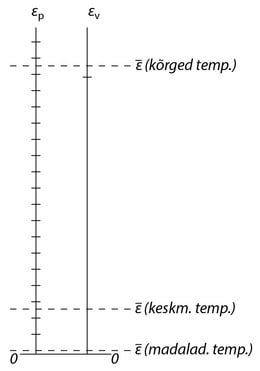
Intervallid energia ükskute lubatud väärtuste ehk, nagu neid nimetatakse, energiatasemete vahl on võnkumise puhul umbes järgu võrra suuremad kui pöörlemise korral. Joonisel 234 on kujutatud kaheaatomilise molekuli pöörlemise ja võnkumise energiatasemete lihtsustatud skeem.

Nagu alajaotuses 106 näeme, on gaasi molekulid jaotatud energiate järgi nii, et enamiku molekulide energia on lähedane keskmisele väärtusel $¯ ¯ ¯ ε$ , vaid väikese osa energia ületab oluliselt $¯ ¯ ¯ ε$ , Et oleks võimalik suurem osa molekule tõmmata pöördliikumisse või võnkumisse, peab nende keskmine energia olema küllalt suur, võrreldes vastavate energiatasemete vahega.

Vaatleme nii madalat temperatuuri, et molekuli keskmine energia $¯ ¯ ¯ ε$ on palju väiksem kui pöörlemisenergia esimene lubatud väärtus (vt. alumist punktiirjoont joonisel 234). Siis tõmmatakse ainult väga väike osa kõikidest molekulidest pöördliikumisse, nii et praktiliselt kõik molekulid võtavad osa üksnes kulgliikumisest. Väikesed temperatuurimuutused kutsuvad esile vaid kulgliikumise energia muutusi ning gaasi soojusmahtuvus säilitab väärtuse $\frac{3}{2} R$ ( vt. piirkonda 1-1' joonisel 233 kujutatud kõveral.

Temperatuuri tõusu saadab $¯ ¯ ¯ ε$ kasv, mistõttu aina suurem osa molekule hakkab pöörlema. Sellele protsessile vastab kõvera piirkond 1'-2 joonisel 233.

Pärast seda, kui kõik molekulid on haaratud pöördliikumisse, algab horisontaalne piirkond 2-2'. Sellele vastavatel temperatuuridel on $¯ ¯ ¯ ε$ veel palju väiksem kui võnkumise energiatasemete vahe, mistõttu molekulide võnkumist praktiliselt ei esine. Edasisel temperatuuritõusul hakkab ikka rohkem ja rohkem molekule võnkuma, sellele olukorral vastab soojusmahtuvuse kõvera üleminekupiirkond 2'-3. Lõpuks, küllalt kõrgel temperatuuril võtavad kõik molekulid osa võnkliikumisest ning soojusmahtuvus saab väärtuseks $\frac{7}{2} R$ .

Pöördudes tagasi klassikalise soojusmahtuvuse teooria juurde, võib öelda, et selle tulemused on ligikaudselt õiged vaid üksikutes temperatuuriintervallides, kusjuures igale intervallile vastab oma vabadusastmete arv.