Õpiku eelmistes osades oleme võrrelnud erinevate elektromagnetlainete liikide energiaid. Oleme maininud ka seda, et valguse kiirgumisel ja neeldumisel tuleks rääkida pigem valguse kvandi ehk footoni energiast. Ühtlasi oleme uurinud elektromagnetlainete spektreid ja spektrijoonte intensiivsusi ning uurinud aatomis elektronide energiatasemeid. Vaatame nüüd täpsemalt üle, mida selle all mõeldakse, kui räägitakse elektromagnetlainete energiast.
Vaatame esmalt uuesti üle valguse tekke aatomis. Elektromagnetlainete spektri uurimisel selgitasime, et nähtav valgus tekib, kui elektronid lähevad üle kõrgematelt energiatasemetelt madalamatele. Et sellised üleminekud võimalikud oleks, on vaja anda elektronile lisaenergiat. Kiirgumisel vabaneb sama palju energiat kui kulub ergastamiseks. Ühe ülemineku puhul on tegu väga konkreetse energia hulgaga ja see ei saa olla suurem ega väiksem neeldunud või kiirgunud energiast. Seda konkreetset portsu energiat on hakatud nimetama kvandiks. Võib öelda, et elektronide energiatasemed aatomis on kvanditud – nad saavad olla kas ühe või teise energiaga, aga mitte kunagi midagi vahepealset. Kui tuua paralleel igapäevaelust, võime näiteks öelda, et õpilaste olek koolis on kvanditud: ollakse kas 11. või 12. klassis, aga mitte vahepeal 11,3. või 11,9. klassis.
Ka valguse kvandi nimetus on siin õpikus juba mitut puhku kõlanud: valguse kvanti nimetatakse footoniks. Kui käsitleme valguse kiirgumist mikrotasemel, siis saame väita, et valgus on footonite voog. Energia neeldumise või kiirgumise kvanditud iseloom seletab ära ka spektrijooned. Igale elektroni üleminekule vastab üks kindel spektrijoon, millel on konkreetne lainepikkus ja sagedus ning seega ka konkreetne energia väärtus.
Elektronide üleminekutel energiatasemete vahel kiirguvad footonid, mille energia on vahemikus . Footoni energia sõltub võrdeliselt elektromagnetlaine sagedusest. Valem, mis seda seost kirjeldab, on Plancki valem:
kus on footoni energia ja Plancki konstant; .
Kui kasutame džaulide asemel elektronvolte, on Plancki konstandiks
Max Planck (1858–1947) oli kvantfüüsika rajaja. Kvantfüüsika seaduspärasustega puutume kokku lähemalt füüsika järgmistes kursustes.
1. näidisülesanne
Lahendus
Kuna aatom neelab ja kiirgab sama energiaga footoni, on kiirgunud footoni energia samuti . Kasutame Plancki valemit
ja Planck konstanti
Arvutades saame
Kuna valguse värvuse määramine on mugavam lainepikkuse kaudu, leiame ka selle valemist
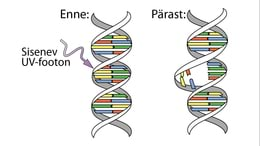
See spektrijoon asub elektromagnetlainete spektri UV-kiirguse osas.
Panete kindlasti tähele, et vahel me räägime valgusest kui lainest, siis jälle kui footonite voost. Kumb see siis lõpuks on? See küsimus on vaevanud teadlasi alates 17. sajandist. Ilmselt on kõige õigem vastus, et valgus ei ole kumbki, valgus on valgus. Looduse uurijatena loome vaid mudeleid valgusega seotud nähtuste seletamiseks ja kirjeldamiseks. Valguse polarisatsiooni, difraktsiooni ja interferentsi seletamiseks on mugavam rakendada mudelit, kus valgus on laine. Joonspektrite seletamiseks tuleks rääkida valgusest kui footonite voost.
Kui võtta peegeldumise seletamiseks appi footoni mudel, tuleks peegeldumist kirjeldada järgmiselt: kui footon jõuab pinnale, neeldub see pinna aatomi elektronkattes, andes oma energia elektronile. Elektron omakorda kiirgab välja footoni, mis ei ole see sama footon, vaid uus, mille tõenäolisem liikumissuund on selline, nagu ütleb meile peegeldumisseadus.
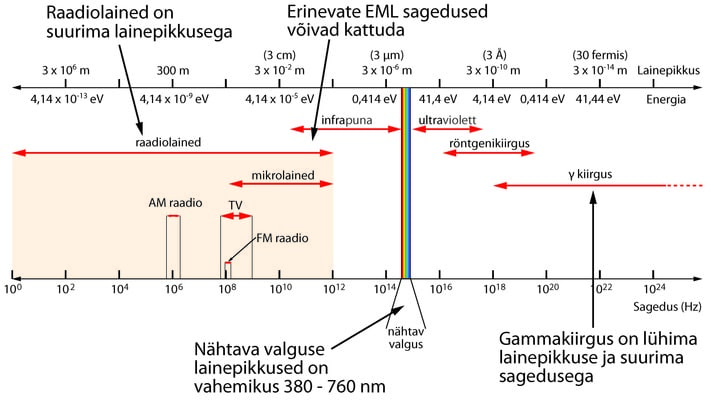
Tegelikult on kõiki elektromagnetlainete liike võimalik käsitleda nii lainete kui ka footonitena. Nii räägitakse sageli gammakvandist või suure energiaga röntgenkiirguse footonitest. Raadiolainete korral raadiokvandi mõistet ei kasutata, sest sellise kvandi energia on väga väike ja mikromaailmas pole protsesse, mida oleks võimalik selliste energiatega käivitada. Üldiselt avalduvadki osakese omadused pigem suurema sagedusega elektromagnetkiirguste korral ja lainelised omadused madala sagedusega kiirguste ehk raadiolainete korral.
Kuidas on seotud footonite energia ja elektromagnetlainete intensiivsus? Mida rohkem footoneid ajaühikus meile silma jõuab, seda intensiivsem on valgus. Samas kui tegu on näiteks punase ja väga intensiivse valgusega, on iga üksiku footoni energia ikkagi madal, ja olgu neid rohkem või vähem, elektrone ei ole nende abil molekulidest välja lüüa võimalik. Kui rasket kivi võib aidata tõsta see, et kutsud kolm sõpra appi, siis kui elektroni ergastamiseks on vaja näiteks energiat, ei piisa isegi miljonist footonist – elektronide energiatasemed aatomis on kvanditud ja aatomi ergastamiseks on vaja n-ö õige energiaga footonit.
Alljärgnevalt on uuesti näha meile juba tuttav elektromagnetlainete skaala, kuhu on lisaks lainepikkustele ja sagedustele märgitud ka vastavate footonite energiate väärtused elektronvoltides (joonis 3.46). Näeme, et nähtava valguse footoni energia on suurusjärgus , raadiolainete energia väärtused aga jäävad vahemikku mikroelektronvolt kuni pikoelektronvolt.
Tabelis 3.2 on toodud molekulide või aatomitega toimuvate liikumiste või muutustega seotud energiate ligikaudsed väärtused.
Kui võrrelda tabeli andmeid elektromagnetlainete energiatega, saame teha mitmeid olulisi järeldusi.
a) IP-kiirguse energiast piisab osakeste rotatsiooni või vibratsiooni energia muutmiseks ehk soojusliikumise suurendamiseks.
b) Selleks, et lõhkuda molekulidevahelisi sidemeid, näiteks sulatada jääd, piisab IP-kiirgusest. Tugevamate sidemete lõhkumiseks, näiteks plastmassi lagundamiseks, on vaja suuremaid energiaid ehk pigem UV-kiirgust. Kui plastist esemed on vees või kaetud näiteks mullaga, ei ole lootustki, et plastik valguse toimel laguneks.
c) Keemilisi reaktsioone vallandavad kiirgused alates nähtavast valgusest kuni gammakiirguseni välja.
d) Suure energiaga gammafootonid võivad põhjustada muutusi aatomituumades, mille seoseenergiaid mõõdetakse megaelektronvoltides.
Valguse kvantmudeliga on seletatav fotoefekti nähtus, kus footon lööb elektrone ainest välja ainult sellisel juhul, kui elektron neelab footoni energia ja sellest energiast piisab nii keemilise sideme lõhkumiseks kui ka elektronile vajaliku kineetilise energia andmiseks. Valguse kvantmudeliga on seotud mitmed olulised rakendused, nagu päikesepatareid ja valguse registreerimiseks kasutatavad CCD-sensorid.
a) Kui valgustada juuksekarva laseriga paari meetri kauguselt, tekib juuksekarva taga olevale ekraanile interferentsipilt.
b) Naatriumilambi spektri kollase valguse spektriosas on iseloomulik kaksikjoon.
c) Vikerkaare teke.
d) Öönägemisseadmetes muudetakse IP-kiirgus nähtavaks valguseks (tavaliselt roheliseks).
e) Röntgenkiirguse neeldumine ionosfääris.