Joone lugu
Ülevaade
Learning focus: | Information about the motion of an object can be summarised on a distance-time graph: the plot shows the object’s distance from the start at a given time and the slope (gradient) at that point shows its speed. |
Observable learning outcome: | Describe motion of an object represented by straight lines on a distance-time graph. |
Question type: | Simple multiple choice |
Key words: | Distance, time, graph |
Mida ütlevad uuringud
It is common for students to view motion graphs as pictures that link to existing physical knowledge of a situation. (Lingefjard and Farahani, 2018; Stump, 1999; Brasell, 1987; Clement, 1986) For example Clement (1986) found that 28% of 12- to 14-year-olds (n=25) drew an up-hills and down-hills picture of a cycle route when asked to draw a speed-distance graph. Likewise Lingefjard and Farahani (2018) found that 35% of 18-year-olds (n=17) interpreted distance-time graphs intuitively as if they were pictures.
Often text books (and teachers) put great attention on the procedures for plotting graphs and calculating gradients, rather than developing understanding of relationships that a graph shows (Stump, 1999). It can be more constructive to concentrate on the latter, which involves teaching:
- understanding of how to read information directly from a graph, interpreting each axis individually
- how to describe simple relationships between the axes such as those represented by straight lines
- how to interpret a graph, linking what it represents to a real situation (Friel, Curcio and Bright, 2001; Lingefjard and Farahani, 2018)
This question investigates students’ understanding of how graphs represent real situations.
Kuidas seda töölehte kasutada
Students should complete the question individually. This could be a pencil and paper exercise, or you could use an electronic ‘voting system’ or mini white boards and the PowerPoint presentation.
The answers to the question will show you whether students understood the concept sufficiently well to apply it correctly.
If there is a range of answers, you may choose to respond through structured class discussion. Ask one student to explain why they gave the answer they did; ask another student to explain why they agree with them; ask another to explain why they disagree, and so on. This sort of discussion gives students the opportunity to explore their thinking and for you to really understand their learning needs.
Differentiation
You may choose to read the questions to the class, so that everyone can focus on the science. In some situations it may be more appropriate for a teaching assistant to read for one or two students.
Kuidas edasi
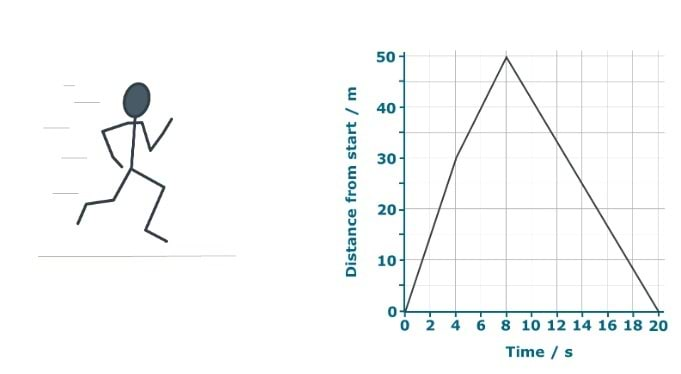
For question 1 answer A suggests students are interpreting the graph as a picture of Zara’s run. Answer B shows a reading taken from the graph without considering how Zara has moved since point X. Answer C shows that her change of distance has been worked out, but time taken has not.
In question 2 students who do not give the correct answer may be interpreting the graph as a picture and be imagining that Z at a place to the right of the starting point. Students may think this even if they interpreted question 1 correctly, because question 1 can be answered correctly by following mathematical procedure, without full understanding. The wrong answer C suggests the understanding that Zara has run 50m away and then 50m further with no regard for direction. Answer B suggests the second part of the graph has been ignored.
If students have misunderstandings about how to describe motion of an object represented by straight lines on a distance-time graph, one strategy to overcome this is to use motion sensors and data-loggers to plot real-time graphs of motion. Students can practise predicting the shape of graph for different descriptions of motion and also reproduce the shape of given graphs by moving in front of a motion sensor. The following BEST ‘response activity’ could be used to do this in follow-up to this diagnostic question:
Response activity: Speedy graphs
Viited
The effect of real-time laboratory graphing on learning graphic representations of distance and velocity
Brasell, H. (1987). The effect of real-time laboratory graphing on learning graphic representations of distance and velocity. Journal of Research in Science Teaching, 24(4), 385-395.Making Sense of Graphs: Critical Factors Influencing Comprehension and Instructional Implications
Friel, S. N., Curcio, F. R. and Bright, G. W. (2001). Making Sense of Graphs: Critical Factors Influencing Comprehension and Instructional Implications. Journal for Research in Mathematics Education, 32(2), 124-158.