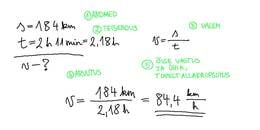
Kui suur on keskmine kiirus, kui sõita Tartust Tallinna 2 tunni ja 11 minutiga?
Tavaline füüsika ülesanne, arvatavasti üks esimesi, mida kiiruse teemat käsitledes võib lahendada. Kiiruse teema on õpilastele tuttav matemaatika ja loodusõpetuse tundidest, midagi keerulist siin ei ole. Pigem võiks keskenduda füüsika ülesannete lahendamise heale tavale.
[Kui pikk on tee Tartust Tallinna? Aastakümneid on teatud ja ka paljud teedeatlased ütlevad, et see tee on 186 kilomeetrit pikk. Aga linnad ei ole punktid, kuhu siis tuleks alustuseks mõõdulindi ots maha panna ja kuhu tõmmata finišijoon? Briti impeeriumi hiilgeaegadest pärineb väga laialt levinud ja kaua kestnud traditsioon mõõta linnade vahelist kaugust ühest peapostkontori eesukse trepist teiseni. Paraku on ajad muutunud ja postkontorid, mida nüüd nimetatakse postisorteerimise keskusteks, pole enam auväärsed hooned linna keskväljakul, vaid tihti poolrobootilised tehased linnaäärsetel tühermaadel. Aga see postkontorite vaheline tee Tartust Tallinna on tõepoolest praegugi 186 km 2021. aastal juba 183 km ja paistab lühenevat.
Kui mõõta kaugus bussijaamade vahel või kõhutunde järgi linnade keskelt (Raekoja plats – Viru väljak), on kaugus 184 km. kõigest 180 km. Eks ole viimasel ajal teeremontidega kurve laugemaks tõmmatud ja asulatest sõidetakse üha rohkem mööda.]
Lisaülesanne
Arvutus eeldaks justkui ühtlase kiirusega sõitmist. Tegelikult ei saa maanteedel kuigi pikalt ühtlase kiirusega sõita ja vastuseks on hoopis keskmine kiirus.
Oletame, et poole teest saab sõita keskmiselt 80km/h. Siis läheb pimedaks ja hakkab sadama märga lund. Teine pool teest tuleb sõita keskmiselt 70km/h. Kui palju on siis keskmine kiirus kogu teel?
Tundub, et kiiruste keskmine ja keskmine kiirus ei erine kuigi palju. Tasub siis üldse juukskarva lõhki ajada? Vaatame ühte vähemelulist näidet, et saada aimu kuidas erinevad mõisted pool teed ja pool aega.
Tähtis saadetis on vaja viia Tallinnast Tartusse. Pool teed kannab seda Ülemiste Vanake, liikudes kiirusega 4km/h. Siis võtab üle Tartu Vaim, kes kihutab teise poole püssikulli kiirusel 600m/s=2160km/h. Kui suur on saadetise keskmine kiirus kogu teel?
Võttes nüüd kiiruste keskmise (vale arvutus), saame 1082km/h. Ilmselgelt pole sel tulemusel mingit füüsikalist sisu. Arvutades eraldi esimese ja teise teekonna poole ajad, saame, et vanakesel kulub 23 tundi, aga vaimul umbes 2,5 minutit. Kokku on tähtis saadetis teel 23,043h ja keskmiseks kiiruseks tuleb ~8km/h (7,99km/h, kui täpsust taga ajada).
Lõpetuseks. Tartust Tallinna on vaja saata üks signaal. Poole teest läbib see valgusvälgatusena mööda optilist kiudu. Seal teeb suur põrgumasin nii kõva paugu, et see kostab Tallinna ära. Kui suur on signaali keskmine liikumiskiirus ja kaua aega kulub kohalejõudmiseni?
Lisame siis veel sama arvutuse teistpidi. Vana autoloks roomab ülesmäge 1 miili keskmise kiirusega 15 mph. Jõudnud üles, sõidab ta 1 miili allamäge ja jaksab nüüd muidugi liikuda kiiremini. Kui suure kiirusega peaks ta laskuva teepoole läbima, et keskmine kogu teel tuleks 30 mph.
Selle ülesande saatis psühholoog Max Wertheimer 1934. aastal Albert Einsteinile. Arvatavasti oleks võinud Einstein ülesandesse peidetud väikese triki kohe ära tabada, aga nii ei läinud. Väidetavalt tuli ahnii-efekt alles siis, kui ta oli vastuse korralikult välja arvutanud. Asi seegi.