Vedelikud ja gaasid (voolised)

Füüsiku pilguga

Surfaja põlvitab kannatlikult oma lainelaual püüdmaks järgmist suurt lainet. Kui ta märkab tulemas taolist kõrgust kasvatavat lainet, sõuab ta ruttu kalda suunas nii, et ta liiguks pea sama kiiresti kui laine, kui too hakkab teda kaasa viima. Siis tõuseb ta laual püsti, pidevalt tasakaalu hoides. Mis viisil saab ta jätkata laine peal sõitmist? Ja kuidas saab ta sealjuures liikuda üles või alla mööda lainepinda? Lühidalt, kuidas surfaja surfab?

Vedelike ja gaaside (vooliste) füüsika on aluseks hüdraulikale, tehnikaharule, mida rakendatakse paljudel elualadel. Tuumaenergeetika insener tunneb huvi vedeliku voolamise vastu vanaldase tuumareaktori hüdraulikasüsteemis, meditsiinitehnoloog huvitub vere voolamisest vanaldase patsiendi arterites. Keskkonnatehnoloog tunneb muret, milline on prügimäe drenaaži või kuivenduse mõju põllumaadele. Merendusspetsialist muretseb ohtude pärast, mis varitsevad süvasukeldujat, või võimaluste pärast, mis on uppunud allveelaeva meeskonnal laevast pääsemiseks. Lennundusinsener võib konstrueerida hüdraulilist süsteemi, mis juhib tiivatüüre ja võimaldab reaktiivlennukil maanduda. Hüdraulikat kasutatakse ka paljudes suurejoonelistes etendustes, kus tohutuid lavakonstruktsioone tõstavad ja langetavad just hüdraulilised süsteemid.

Enne kui saame uurida vooliste füüsika selliseid rakendusi, peame vastama esimesele küsimusele: „Mis on voolis?”

Mis on voolis?

Voolis, vastandina tahkisele, on aine, mis võib voolata, s.t vedelik või gaas. Voolised võtavad selle (suvalise) mahuti kuju, millesse me neid paigutame. Need teevad seda seetõttu, et voolis ei suuda vastu seista tema pinna suhtes tangentsiaalsetele (pinna puutuja suunalistele) jõududele. (Punktis 12-7 sisse toodud rangemates määratlustes on voolis aine, mis voolab, kuna ei suuda vastu seista nihkepingele. Ta võib aga avaldada jõudu pinnaga risti olevas suunas.) Mõned materjalid, nagu näiteks pigi, vajavad palju aega, enne kui nad omandavad mahuti kuju, aga lõpuks nad seda teevad; seetõttu liigitame me isegi neid materjale voolisteks.

Te võite imestada, miks paneme me vedelikud ja gaasid kokku ja kutsume neid voolisteks. Lõppude lõpuks (võite te öelda) erineb vedel vesi ju nii jääst kui ka aurust. Tegelikult ei ole see nii. Jääs, nagu kõikides teisteski kristalltahkistes, on aatomid korrastatud vägagi jäika kolmemõõtmelisse struktuuri, mida kutsutakse kristallvõreks. Ei aurus ega vedelas vees pole aga sellist suure ulatusega korrastatust.

Tihedus ja rõhk

Kui me kõneleme jäikadest kehadest, siis peame silmas selliseid aineklompe nagu näiteks puuklotsid, pesapallid või metallvardad. Neid iseloomustavad füüsikalised suurused, mida me peame kasulikuks ja mille kaudu me avaldame Newtoni seadused, on mass ja jõud. Me võime näiteks öelda, et klotsile massiga $3, 6 kg$ mõjub jõud $25 N$ .

Vooliste korral oleme me rohkem huvitatud omadustest, mis võivad eri punktides aine sees olla erineva väärtusega. Mõisted, mis on siin kasulikumad kui mass ja jõud, on tihedus ja rõhk.

Tihedus

Leidmaks voolise tihedust $ρ$ suvalises punktis, eraldame selle punkti ümber välja väikese ruumielemendi ruumalaga $Δ V$ ja määrame selles ruumielemendis sisalduva voolise massi $Δ m$ . Tihedus on siis

(14-1)

ρ = \frac{Δ m}{Δ V}

Teoorias on voolise tihedus mingis punktis selle suhte piirväärtus ruumala muutumisel järjest väiksemaks. Praktikas eeldame me, et voolise poolt täidetud ruumiosa ulatus on suur võrreldes aatomite mõõtmetega ja seetõttu on voolis „sile” (ühtlase tihedusega), mitte aga aatomite kaupa klompjas. See eeldus lubab meil võrduse 14-1 esitada kujul

(14-2)

ρ = \frac{m}{V}

kus $m$ ja $V$ on vastavalt voolisenäidise mass ja ruumala.

Tihedus on skalaarne suurus, selle ühik SI-süsteemis on kilogramm kuupmeetri kohta. Tabelis 14-1 on toodud mõnede ainete tihedused ja mõnede objektide keskmised tihedused. Pange tähele, et gaasi tihedus (vt tabelis „Õhk”) muutub märgatavalt sõltuvalt rõhust, aga vedeliku tihedus (vt „Vesi”) mitte; st gaasid on hõlpsasti kokkusurutavad, vedelikud aga mitte.

TABEL 14-1 Mõned tihedused

Materjal või objekt		Tihedus ( $k g / m^{3}$ )
Tähtedevaheline ruum		$10^{- 20}$
Parim laboratoorne vaakum		$10^{- 17}$
Õhk:	$20^{\circ}$ ja rõhk $1 a t m$	$1, 21$
	$20^{\circ}$ ja rõhk $50 a t m$	$60, 5$
Vahtpolüstüreen		$1 \times 10^{2}$
Jää		$0, 917 \times 10^{3}$
Vesi:	$20^{\circ}$ ja rõhk $1 a t m$	$0, 998 \times 10^{3}$
	$20^{\circ}$ ja rõhk $50 a t m$	$1, 000 \times 10^{3}$
Merevesi:	$20^{\circ}$ ja rõhk $1 a t m$	$1, 024 \times 10^{3}$
Veri		$1, 060 \times 10^{3}$
Raud		$7, 9 \times 10^{3}$
Elavhõbe		$13, 6 \times 10^{3}$
Maakera:	keskmine	$5, 5 \times 10^{3}$
	tuum	$9, 5 \times 10^{3}$
	maakoor	$2, 8 \times 10^{3}$
Päike:	keskmine	$1, 4 \times 10^{3}$
	tuum	$1, 6 \times 10^{5}$
Valge kääbustäht (tuum)		$10^{10}$
Uraani aatomi tuum		$3 \times 10^{17}$
Neutrontäht (tuum)		$10^{18}$

Rõhk

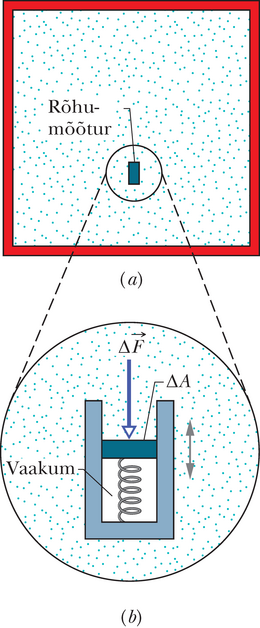
Olgu väike rõhumõõtur riputatud voolisega täidetud anumasse, nagu näidatud joonisel 14-1a. Mõõtur (joonis 14-1b) koosneb kolvist pindalaga $Δ A$ , mis liigub tihedalt sobitatud silindris ja toetub vastu vedru. Nihkeandur lubab määrata kolvi nihet, mille võrra (kalibreeritud) vedru on ümbritseva voolise poolt kokku surutud, näidates sel viisil kolvile voolise poolt mõjuva normaaljõu suurust $Δ F$ . Me defineerime kolvile mõjuva voolise rõhu kui

(14-3)

p = \frac{Δ F}{Δ A}

Teoorias on rõhk suvalises voolise punktis selle suhte piirväärtus juhul, kui sellesse punkti asetatud kolvi pindala muudetakse järjest väiksemaks. Kui aga jõud on ühtlane üle kogu tasase pinna $A$ , siis võime seose 14-3 esitada kujul

(ühtlase jõu rõhk tasapinnale, 14-4)

p = \frac{F}{A}

kus $F$ on pindalale $A$ mõjuva normaaljõu suurus. (Kui me ütleme, et jõud on ühtlane üle pinna, siis tähendab see jõu ühtlast jaotust üle pinna kõigi punktide.)

Katseliselt on leitav, et liikumatu voolise etteantud punktis valemiga 14-4 määratud rõhu arvuline väärtus ei sõltu mõõturi orientatsioonist. Rõhk on skalaar, millel pole suunasõltuvust. Muidugi on tõsi, et meie rõhumõõturi kolvile mõjuv jõud on vektorsuurus, kuid valem 14-4 sisaldab vaid selle jõu tugevust, mis on skalaarne suurus.

SI-süsteemis on rõhu ühikuks njuuton ruutmeetri kohta ja sellele on antud spetsiaalne nimetus, paskal ( $P a$ ). Meetermõõdustikku kasutavates maades on mõõturid rõhu määramiseks autorehvides kalibreeritud kilopaskalites. Paskal on seotud mõnede teiste kasutusel olevate (mitte-SI) rõhuühikutega järgmiselt:

1 a t m = 1, 01 \times 10^{5} P a = 760 t o r r = 14, 7 l b / i n^{2}

Atmosfäär ( $a t m$ ) on, nagu nimi viitab, ligikaudne keskmine õhurõhk merepinnal. Torr (nimetatud Evangelista Torricelli järgi, kes leiutas elavhõbebaromeetri aastal 1674) kannab ka nimetust millimeeter elavhõbedasammast ( $m m H g$ ). Nael ruuttolli kohta ( $l b / i n^{2}$ ) on sageli lühendatud kui $p s i$ . Tabelis 14-2 on toodud mõned rõhud.

TABEL 14-2 Mõned rõhud

	Rõhk ( $P a$ )
Päikese kese	$2 \times 10^{16}$
Maakera kese	$4 \times 10^{11}$
Kõrgeim laboris hoitud rõhk	$1, 5 \times 10^{10}$
Sügavaim ookeanisüvik (põhjas)	$1, 1 \times 10^{8}$
Tikk-kontsad tantsupõrandal	$10^{6}$
Autorehv^a	$2 \times 10^{5}$
Atmosfäär merepinnal	$1, 0 \times 10^{5}$
Normaalne süstoolne vererõhk^a,b	$1, 6 \times 10^{4}$
Parim laboratoorne vaakum	$10^{- 12}$

^a Rõhk lisaks atmosfäärirõhule

^b Vastab väärtusele $120 t o r r i$ meditsiinilisel vererõhumõõtjal

Näidisülesanne 14-1

Elutoa põranda mõõtmed on $3, 5$ ja $4, 2$ meetrit ning kõrgus $2, 4 m$ .

Kui palju kaalub ruumis olev õhk, kui õhurõhk on

1, 0 atm

Lahendus

JUHTMÕTE (1) Õhu kaal on $m g$ , kus $m$ on õhu mass. (2) Mass $m$ on seotud õhu tihedusega $ρ$ ja selle ruumalaga $V$ valemiga 14-2 ( $ρ = m / V$ ).

Arvutused: Pannes need kaks ideed kokku ja võttes õhu tiheduse $1, 0 atm$ jaoks tabelist 14-1, saame

m g = (ρ V) g = (1, 21 k g / m^{3}) (3, 5 m \times 4, 2 m \times 2, 4 m) (9, 8 m / s^{2}) = 418 N \approx 420 N - ---- - - ---- -

See on umbes $110$ Pepsi-purgi kaal.

Kui suur on allapoole suunatud jõud, mis mõjub atmosfääri poolt teie pealaele, mille pindalaks võtame

0, 040 m^{2}

Lahendus

JUHTMÕTE Kui voolise rõhk $p$ pinnale pindalaga $A$ on ühtlane, saab voolise poolt pinnale mõjuva jõu leida valemist 14-4 ( $p = F / A$ ).

Arvutused: Kuigi õhurõhk päevast päeva varieerub, võime ligikaudu võtta $p = 1, 0 atm$ . Valem 14-4 annab siis

F = p A = (1, 0 atm) (\frac{1, 01 \times 10^{5} N / m^{2}}{1, 0 atm}) (0, 040 m^{2}) = 4, 0 \times 10^{3} N - ----------- - - ----------- -

See hiigeljõud võrdub õhusamba kaaluga, mis katab teie pealage ja ulatub läbi kogu atmosfääri.

Liikumatud voolised

JOONIS 14-2 (a) Veepaak, milles vaatlusalune veeosa sisaldub kujuteldavas horisontaalse alusega (pindala $A$ ) silindris. Jõud ${\to F}_{1}$ mõjub silindri ülemisele tahule, jõud ${\to F}_{2}$ silindri alumisele tahule; silindris olevale veele mõjuvat raskusjõudu kujutab vektor $m \to g$ . (b) Veeosale mõjuvate jõudude vektordiagramm.

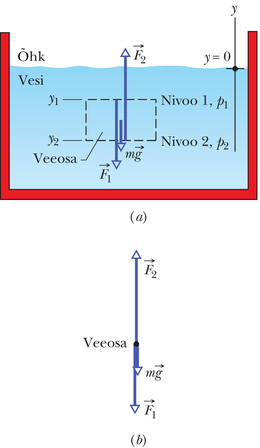
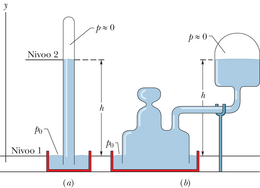
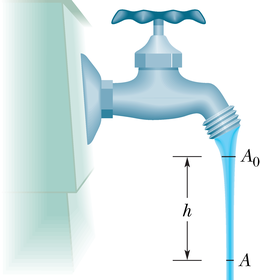
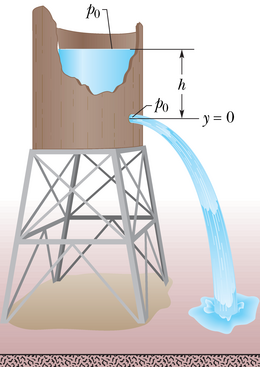
Joonisel 14-2a on kujutatud vee või mõne muu vedelikuga täidetud paaki, mis on avatud välisõhule. Iga sukelduja teab, et rõhk kasvab sügavusega veepinnast. Sukelduja sügavusmõõtja on tegelikult rõhumõõtur, mis sarnaneb joonisel 14-1b kujutatuga. Nagu teab iga mägironija, kahaneb õhurõhk kõrgusega, kui ta tõuseb atmosfääris ülespoole. Rõhkusid, mida kogevad sukelduja ja mägironija, kutsutakse hüdrostaatilisteks rõhkudeks, kuna nad on põhjustatud voolistest, mis on staatilised (liikumatud). Soovime siinkohal leida avaldise hüdrostaatilise rõhu jaoks sügavuse või kõrguse funktsioonina.

Vaatleme esmalt rõhu kasvu sõltuvalt sügavusest allpool veepinda. Valime paagis vertikaalse $y$ -telje nullpunktiga veepinnal ja positiivse suunaga ülespoole. Vaatleme nüüd vee seda osa, mis asetseb kujuteldavas püstsilindris, mille otspinnad on horisontaalsed ringid pindalaga $A$ , kus $y_{1}$ ja $y_{2}$ (mõlemad negatiivsed arvud) on vastavalt silindri ülemise ja alumise pinna sügavused.

Joonisel 14-2b on esitatud silindris olevale veeosale mõjuvate jõudude vektordiagramm. Vesi on staatilises tasakaalus, s.t on liikumatu ja talle mõjuvad jõud on tasakaalus. Vertikaalselt mõjuvad kolm jõudu: jõud ${\to F}_{1}$ mõjub silindri ülemisele tahule ja tema tekitajaks on silindri kohal asuv vesi. Sarnaselt mõjub jõud ${\to F}_{2}$ silindri alumisele tahule ja on põhjustatud silindrist allpool olevast veest. Silindris olevale veele mõjuv raskusjõud on esitatud vektoriga $m \to g$ , kus $m$ on silindris oleva vee mass. Jõudude tasakaal avaldub seosena

(14-5)

F_{2} = F_{1} + m g

Teisendame valemi 14-5 kujule, mis sisaldab rõhke. Valemist 14-4 teame, et

(14-6)

F_{1} = p_{1} A

(14-6)

F_{2} = p_{2} A

Valem 14-2 ütleb, et vee mass silindris on $m = ρ V$ , kus silindri ruumala on tema otspinna pindala $A$ ja kõrguse $y_{1} - y_{2}$ korrutis. Seega avaldub $m$ kujul $ρ A (y_{1} - y_{2})$ . Asetades selle ja valemi 14-6 valemisse 14-5, leiame

p_{2} A = p_{1} A + ρ A g (y_{1} - y_{2})

ehk

(14-7)

p_{2} = p_{1} + ρ g (y_{1} - y_{2})

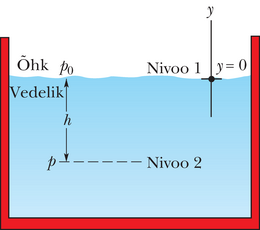
Seda valemit saab kasutada rõhu leidmiseks nii vedelikus (sügavuse funktsioonina) kui atmosfääris (kõrguse funktsioonina). Oletame, et esimesel juhul huvitab meid rõhk $p$ sügavusel $h$ vedeliku pinna all. Siis valime me nivoo $1$ asuvana vedeliku pinnal, millele mõjuv atmosfäärirõhk olgu tähistatud $p_{0}$ , ja nivoo $2$ sügavusel $h$ vedeliku pinna all (nagu joonisel 14-3). Asetame

y_{1} = 0, p_{1} = p_{0} ja y_{2} = - h, p_{2} = p

valemisse 14-7, millest

(rõhk sügavusel h, 14-8)

p = p_{0} + ρ g h

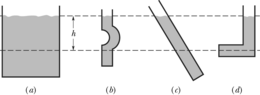
Pange tähele, et rõhk vedelikus mingil sügavusel sõltub sellest sügavusest, kuid ei sõltu mitte mingitest horisontaalsetest mõõtmetest.

Rõhk staatilises tasakaalus oleva vedeliku mingis punktis sõltub selle punkti sügavusest, kuid ei sõltu mahuti või selles oleva vedeliku horisontaalsetest mõõtmetest.

Seega kehtib valem 14-8 mistahes kujuga mahuti korral. Kui mahuti põhi asub sügavusel $h$ , siis valem 14-8 annab seal mõjuva rõhu $p$ .

JOONIS 14-3 Rõhk $p$ kasvab koos sügavusega $h$ allpool vedeliku pinda vastavalt valemile 14-8.

Rõhku $p$ valemis 14-8 nimetatakse kogurõhuks või absoluutseks rõhuks nivool $2$ . Selgitamaks miks, pange tähele, et rõhk $p$ nivool $2$ koosneb kahest osarõhust: (1) vedelikule mõjuvast õhurõhust $p_{0}$ ja (2) nivoo $2$ kohal asuvast vedelikust põhjustatud rõhust $ρ g h$ . Üldiselt kutsutakse vahet absoluutse rõhu ja atmosfäärirõhu vahel manomeetriliseks rõhuks. (Nimetus tuleneb manomeetri kasutamisest selle rõhuvahe mõõtmiseks.) Joonisel 14-3 kujutatud olukorras on manomeetriline rõhk $ρ g h$ .

Valem 14-7 kehtib ka vedeliku pinna kohal: ta annab atmosfääri rõhu antud kõrgusel nivoo $1$ kohal rõhu $p_{1}$ kaudu nivool $1$ (eeldades, et atmosfääri tihedus selles kõrguste vahemikus on muutumatu). Näiteks, et leida valemist 14-3 rõhku atmosfääris kõrgusel $d$ nivoost $1$ asendame

y_{1} = 0, p_{1} = p_{0} ja y_{2} = - h, p_{2} = p

Siis, tähistades $ρ = ρ_{˜ o hk}$ , saame

p = p_{0} - ρ_{˜ o hk} g d

Joonis kujutab nelja oliiviõli mahutit. Järjestage nad rõhu järgi sügavusel

h

, suurimast rõhust alustades.

Kogenematu sukelduja hingab basseinis oma õhuballoonist kopsud täis, misjärel jätab ballooni sügavusel

L

maha ja ujub üles veepinnale. Ta eirab juhtnööre ja ei hinga tõusul välja. Kui ta jõuab veepinnale, on vahe välisrõhu ja õhurõhu vahel ta kopsudes

9, 3 k P a

. Milliselt sügavuselt sukelduja startis? Millise potentsiaalse surmaohuga seisab ta silmitsi?

Lahendus

JUHTMÕTE Rõhk sügavusel $h$ vedelikus tihedusega $ρ$ on antud valemiga 14-8 ( $p = p_{0} + ρ g h$ ), kus manomeetriline rõhk $ρ g h$ on lisatud atmosfäärirõhule $p_{0}$ .

Arvutused: Kui sukelduja täidab kopsud sügavusel $L$ , siis on talle mõjuv välisrõhk (ja seega ka rõhk ta kopsudes) suurem kui pinnal ja antud valemiga 14-8

p = p_{0} + ρ g L

kus $p_{0}$ on atmosfäärirõhk ja $ρ$ on vee tihedus ( $998 k g / m^{3}$ tabelist 14-1). Tõusmisel talle mõjuv välisrõhk kahaneb, kuni saab veepinnal võrdseks atmosfäärirõhuga $p_{0}$ . Ta vererõhk kahaneb samuti, kuni muutub normaalseks. Kuna ta aga ei hinga välja, jääb õhk ta kopsudes rõhule, mis oli sügavusel $L$ . Pinnal on vahe kopsudes oleva kõrgema rõhu ja rindkerele mõjuva madalama rõhu vahel

Δ p = p - p_{0} = ρ g L

millest leiame

L = \frac{Δ p}{ρ g} = \frac{9300 P a}{(998 k g / m^{3}) (9, 8 m / s^{2})} = 0, 95 m - ------ - - ------ -

See pole just sügav! Ometi piisab rõhkude vahest $9, 3 k P a$ (umbes $9 %$ atmosfäärirõhust), et rebestada sukelduja kopsud ja suruda seal kõrgel rõhul olevat õhku madalamarõhulisse verre, mis kannab siis õhu südamesse, mille tõttu sukelduja sureb. Kui sukelduja järgib juhendeid ja hingab tõusul järk-järgult välja, võimaldab ta rõhul kopsudes tasakaalustuda välisrõhuga ja oht puudub.

U-toru joonisel 14-4 sisaldab kahte vedelikku staatilises tasakaalus: vesi tihedusega

ρ_{v}

(

= 998 k g / m^{3}

) on paremas harus ja tundmatu tihedusega

ρ_{x}

õli vasakus harus. Mõõtmised andsid

l = 135 m m

d = 12, 3 m m

. Milline on õli tihedus?

Lahendus

JOONIS 14-4 Õlitase vasakus toruharus on kõrgem kui veetase paremas toruharus, kuna õli tihedus on vee omast väiksem. Mõlemad vedelikusambad avaldavad nende lahutuspinnale võrdset rõhku $p_{s e e s}$ .

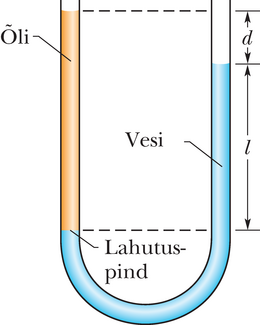
JUHTMÕTTED (1) Rõhk õli-vee lahutuspinnal sõltub õli tihedusest $ρ_{x}$ ja õlisamba kõrgusest lahutuspinna kohal. (2) Paremas harus olev vesi peab samal kõrgusel olema samal rõhul $p_{sees}$ . Põhjuseks on asjaolu, et kuna vesi on staatilises tasakaalus, peavad rõhud samal sügavusnivool asuvates punktides olema võrdsed, isegi kui need punktid pole horisontaali mööda vedelikus ühendatud.

Arvutused: Lahutuspinna nivoo on kaugusel $l$ allpool vee vaba pinda parempoolses harus ja valemist 14-8 saame

p_{sees} = p_{0} + ρ_{v} g l

(parempoolses harus).

Vasakus harus on lahutuspind kaugusel $l + d$ allpool õli vaba pinda ja me saame – jällegi võrrandist 14-8 –

p_{sees} = p_{0} + ρ x g (l + d)

(vasakpoolses harus).

Võrrutades need kaks avaldist ja avaldades tundmatu tiheduse, saame

ρ_{x} = ρ_{v} \frac{l}{l + d} = (998 k g / m^{3}) \frac{135 m m}{135 m m + 12, 3 m m} = 915 k g / m^{3} - --------- - - --------- -

Pange tähele, et vastus ei sõltu atmosfäärirõhust $p_{0}$ ega raskuskiirendusest $g$ .

Rõhu mõõtmine

Elavhõbebaromeeter

Joonisel 14-5a on kujutatud väga lihtne elavhõbebaromeeter – seade atmosfäärirõhu mõõtmiseks. Pikk klaastoru on täidetud elavhõbedaga, pööratud avatud otsaga allapoole ja pistetud elavhõbedaga täidetud anumasse. Torus elavhõbedasamba kohal on vaid elavhõbeda aur, mille rõhk harilikel temperatuuridel on nii väike, et seda pole vaja arvestada.

Me võime kasutada valemit 14-7, leidmaks atmosfäärirõhku $p_{0}$ elavhõbedasamba kõrguse $h$ kaudu. Valime joonisel 14-2 nivooks $1$ õhu ja elavhõbeda lahutuspinna ning nivooks $2$ elavhõbedasamba ülemise pinna, nagu on tähistatud joonisel 14-5a. Asetame nüüd

y_{1} = 0, p_{1} = p_{0}

y_{2} = h, p_{2} = 0

valemisse 14-7 ja leiame

(14-9)

p_{0} = ρ g h

kus $ρ$ on elavhõbeda tihedus.

Etteantud rõhu korral ei sõltu elavhõbedasamba kõrgus $h$ vertikaalse toru ristlõike pindalast. Joonisel 14-5b kujutatud kummalise kujuga elavhõbebaromeeter annab täpselt sama lugemi mis joonisel 14-5a kujutatu: ainus, mis loeb, on vertikaalne vahemaa elavhõbeda nivoode vahel.

Valem 14-9 näitab, et antud rõhu korral sõltub elavhõbedasamba kõrgus vaba langemise kiirenduse väärtusest $g$ baromeetri asukohas ja elavhõbeda tihedusest, mis muutub temperatuuriga. Samba kõrgus (millimeetrites) on arvuliselt võrdne rõhuga (torrides) ainult siis, kui baromeeter asub kohas, kus $g$ väärtus võrdub tema kokkuleppelise standardväärtusega $9, 80665 m / s^{2}$ ja elavhõbeda temperatuur on $0^{\circ} C$ . Kui need tingimused ei kehti (ja seda teevad nad harva), tuleb sisse viia väikesed parandused, enne kui elavhõbedasamba kõrguse saab teisendada rõhuks.

Avatud toru manomeeter

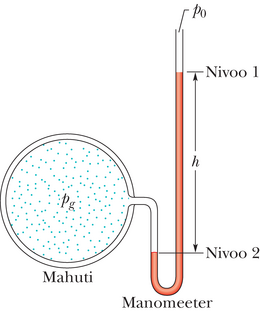
Avatud toru manomeeter (joonis 14-6) mõõdab gaasi manomeetrilist rõhku $p_{man}$ . Ta koosneb vedelikku sisaldavast U-torust, mille üks haru on ühendatud anumaga, milles me soovime manomeetrilist rõhku määrata, teine haru avaneb atmosfääri. Manomeetrilise rõhu leidmiseks joonisel 14-6 näidatud kõrguse $h$ kaudu võime kasutada valemit 14-7. Valime nivood $1$ ja $2$ , nagu näidatud joonisel 14-6. Asendades

y_{1} = 0, p_{1} = p_{0}

y_{2} = - h, p_{2} = p

valemisse 14-7, leiame, et

(14-10)

p_{man} = p - p_{0} = ρ g h

kus $ρ$ on vedeliku tihedus torus. Manomeetriline rõhk $p_{m a n}$ on võrdeline kõrgusega $h$ .

Manomeetriline rõhk võib olla nii positiivne kui negatiivne sõltuvalt sellest, kas $p > p_{0}$ või $p < p_{0}$ . Täispumbatud rehvides ja inimese vereringes on (absoluutne) rõhk atmosfäärirõhust suurem ja seega manomeetriline rõhk positiivne suurus, mõnikord kutsutakse seda ka ülerõhuks. Kui te imete joogikõrre kaudu vedelikku, siis on (absoluutne) rõhk teie kopsudes väiksem atmosfäärirõhust. Manomeetriline rõhk teie kopsudes on siis negatiivne suurus.

Pascal's law

Kui te pigistate hambapasta tuubi selle ühest otsast, et tuubi teisest otsast tuleks pasta välja, jälgite te toimimas Pascali seadust. Sama seadus on aluseks nn Heimlichi võttele, kus kõhule järsult ja õigesti rakendatud surve kandub üle kõrri, paisates jõuga välja selle blokeerinud toidu. Seaduse selgesõnaline esmaesitaja oli Blaise Pascal (kelle nime ka rõhuühik kannab) aastal 1652:

Kinnises anumas asuvale kokkusurumatule voolisele rakendatud rõhumuutus kantakse muutumatult üle voolise igale osale ja tema mahuti seintele.

Pascali seaduse demonstratsioon

JOONIS 14-7 Pliihaavlitega (väikeste pliikeradega) koormatud kolb tekitab rõhu $p_{v ¨ a line}$ kolvi all asuva (kokkusurumatu) vedeliku ülapinnal. Kui $p_{v ¨ a line}$ väärtust suurendatakse, lisades pliihaavleid, kasvab rõhk vedeliku kõigis punktides sama palju.

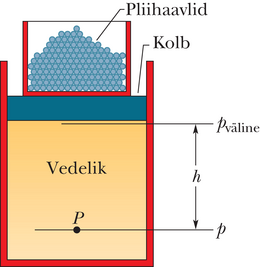
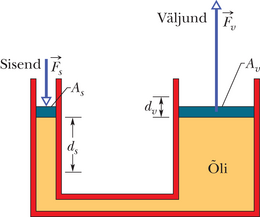
Vaatleme juhtu, kus kokkusurumatu vedelik asub kõrges silindris nagu joonisel 14-7. Silindriga on sobitatud kolb, mille peal on karp pliihaavlitega. Atmosfäär, karp ja pliihaavlid avaldavad kolvile ja seega ka vedelikule rõhku $p_{v ¨ a line}$ . Rõhk $p$ vedeliku mingis punktis on siis

(14-11)

p = p_{v ¨ a line} + ρ g h

Lisame nüüd karpi veel veidi haavleid, et suurendada rõhku $p_{v ¨ a line}$ suuruse $Δ p_{v ¨ a line}$ võrra. Suurused $ρ$ , $g$ ja $h$ võrrandis 14-11 sellest ei muutu, nii et rõhu muutus punktis $P$ on

(14-12)

Δ p = Δ p_{v ¨ a line}

See rõhu muutus on sõltumatu sügavusest $h$ , seega peab seos kehtima kõigi punktide jaoks vedelikus, nagu Pascali seadus väidabki.

Pascali seadus ja hüdrauliline kang

JOONIS 14-8 Hüdrauliline seade, mida saab kasutada jõu ${\to F}_{s}$ võimendamiseks. Tehtavat tööd aga ei võimendata ja see on ühesuurune nii sisend- kui väljundjõu jaoks.

Joonis 14-8 näitab, kuidas Pascali seadust saab kasutada hüdraulilise kangi tööks. Mõjugu töötamisel vasakule (ehk sisend-)kolvile pindalaga $A_{s}$ allapoole suunatud jõud suurusega ${\to F}_{s}$ . Seadmes olev kokkusurumatu vedelik tekitab siis parempoolsele (ehk väljund-)kolvile pindalaga $A_{v}$ mõjuva jõu $F_{v}$ . Süsteemi tasakaalus hoidmiseks peab eksisteerima allapoole suunatud jõud suurusega $F_{v}$ , mis mõjub väljundkolvile välise koormise poolt (mida pole joonisel näidatud). Vasakule kolvile rakendatud jõud ${\to F}_{s}$ ja koormise poolt paremale kolvile mõjuv allapoole suunatud jõud ${\to F}_{v}$ tekitavad vedelikus rõhumuutuse

Δ p = \frac{F_{s}}{A_{s}} = \frac{F_{v}}{A_{v}}

nii et,

(14-13)

F_{v} = F_{s} \frac{A_{v}}{A_{s}}

Valem 14-13 näitab, et koormisele mõjuv väljundjõud $F_{v}$ peab olema suurem kui sisendjõud $F_{s}$ , kui $A_{v} > A_{s}$ , nagu see on joonisel 14-8.

Kui me nihutame sisendkolbi allapoole vahemaa $d_{s}$ võrra, siis väljundkolb liigub üles vahemaa $d_{v}$ võrra nii, et mõlema kolvi juures teisaldatakse võrdne ruumala $V$ kokkusurumatut vedelikku. Siis

V = A_{s} d_{s} = A_{v} d_{v}

mille võime kirjutada kujul

(14-4)

d_{v} = d_{s} \frac{A_{s}}{A_{v}}

See näitab, et kui $A_{v} > A_{s}$ (nagu on joonisel 14-8), siis liigub väljundkolb väiksema vahemaa kui sisendkolb.

Valemitest 14-13 ja 14-14 võime esitada väljundtöö

(14-15)

W = F_{v} d_{v} = (F_{s} \frac{A_{s}}{A_{v}}) (d_{s} \frac{A_{s}}{A_{v}}) = F_{s} d_{s}

mis näitab, et rakendatud jõu poolt sisendkolvi kallal tehtud töö $W$ on võrdne tööga $W$ , mida tehakse väljundkolvi poolt sellele asetatud koormuse tõstmisel.
Hüdraulilisest kangist saadav kasu on järgmine:

Hüdraulilise kangi abil saab teataval teepikkusel mõjuva teatava jõu transformeerida suuremaks jõuks, mis mõjub lühemal teepikkusel.

Jõu ja teepikkuse korrutis jääb samaks, seega tehakse sama hulk tööd. Kuid sageli annab suurema jõu rakendamise võimalus tohutu eelise. Enamik meist ei suuda näiteks tõsta autot vahetult, küll aga suudab seda hüdraulilise tungrauaga, kuigi peame pumpama käepidet palju pikemas ulatuses, kui auto kerkib, ja väikeste liigutuste kaupa.

Archimedese seadus

JOONIS 14-9 Kotile mõjuv raskusjõud peab olema tasakaalustatud ümbritseva vee poolt mõjuva summaarse ülespoole suunatud jõuga.

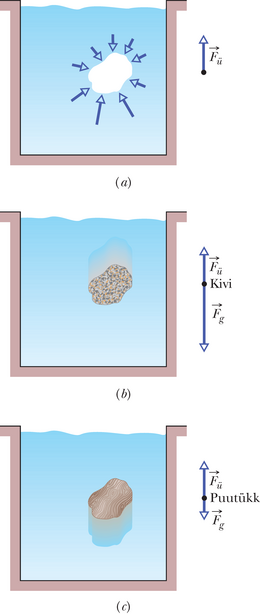
Joonis 14-9 kujutab üliõpilast ujumisbasseinis, kes tegeleb väga õhukese (tühise massiga) kilekotiga, mis on vett täis. Ta leiab, et kott ja selles sisalduv vesi on staatilises tasakaalus, püüdmata ei tõusta ega uppuda. Allpoole suunatud raskusjõud ${\to F}_{g}$ peab olema tasakaalustatud ümbritseva vee poolt kotile mõjuva summaarse ülespoole suunatud jõuga.

JOONIS 14-10 (a) Vees olevat tühimikku ümbritsev vesi avaldab summaarset üleslükkejõudu kõigele, mis tühimikku täidab. (b) Tühimikuga võrdse ruumalaga kivi jaoks ületab raskusjõud suuruselt üleslükkejõu. (c) Sama ruumalaga puutüki jaoks on raskusjõud suuruselt üleslükkejõust väiksem.

See summaarne ülespoole suunatud jõud on üleslükkejõud ${\to F}_{¨ u}$ . See jõud on olemas seetõttu, et rõhk ümbritsevas vees kasvab sügavusega veepinnast. Seega on rõhk koti põhjale suurem kui tema ülaosale, mis tähendab, et suuruselt ületavad koti põhjale rõhu tõttu mõjuvad jõud koti ülaosale mõjuvaid jõude. Mõned neist jõududest on kujutatud joonisel 14-10a, kus koti poolt hõivatud ruumala on jäetud tühjaks. Pange tähele, et koti põhja lähedal kujutatud jõuvektorid (ülespoole suunatud komponentidega) on pikemad kui koti ülaosas kujutatud vektorid (allapoole suunatud komponentidega). Kui vektoriliselt liita kõik vee poolt kotile mõjuvad jõud, siis horisontaalsed komponendid koonduvad välja ja vertikaalsed komponendid annavad liitudes kotile mõjuva ülespoole suunatud üleslükkejõu ${\to F}_{¨ u}$ . (Jõud ${\to F}_{¨ u}$ on joonisel 14-10a kujutatud basseinist paremal.)

Kuna kott veega on staatilises tasakaalus, siis on jõu ${\to F}_{¨ u}$ suurus võrdne raskusjõu ${\to F}_{g}$ suurusega $m_{v} g$ , mis mõjub veekotile: ${\to F}_{¨ u} = m_{v} g$ (alaindeks $v$ viitab siin suvalisele voolisele, antud juhul siis veele). Teisisõnu, üleslükkejõu suurus on võrdne kotis oleva vee kaaluga.

Joonisel 14-10b asendasime veekoti kiviga, mis täpselt täidab joonisel 14‑10a kujutatud tühimiku. Öeldakse, et kivi tõrjub vee välja, pidades silmas asjaolu, et kivi täidab ruumiosa, mida muidu täidaks vesi. Me ei ole midagi muutnud tühimiku kujus, nii et jõud tühimiku pinnal peavad olema samad mis veega täidetud koti korral. Seega seesama üleslükkejõud, mis mõjus veega täidetud kotile, mõjub nüüd ka kivile ja üleslükkejõu suurus ${\to F}_{¨ u}$ on võrdne väärtusega $m_{v} g$ , kivi poolt välja tõrjutud vee kaaluga.

Erinevalt veega täidetud kotist pole kivi staatilises tasakaalus. Allapoole suunatud raskusjõud ${\to F}_{g}$ ületab suuruselt üleslükkejõudu, nagu näidatud kivile mõjuvate jõudude vektordiagrammil (joonis 14-10b). Kivi liigub kiirenevalt allapoole, vajudes basseini põhja.

Täidame järgmisena tühimiku joonisel 14-10a sellesse täpselt sobiva kergekaalulise puitklotsiga, nagu kujutatud joonisel 14-10c. Jällegi, midagi ei muutunud jõududes tühemiku pinnal, seega on üleslükkejõu suurus ${\to F}_{¨ u}$ endiselt võrdne väärtusega $m_{v} g$ , puitklotsi poolt välja tõrjutud vee kaaluga. Sarnaselt kiviga pole ka puuklots staatilises tasakaalus. Sedapuhku on aga raskusjõud ${\to F}_{g}$ suuruselt väiksem üleslükkejõust (nagu näidatud basseinist paremal) ja nii hakkab klots kiirenevalt tõusma ülespoole, veepinnale.

Meie tulemused koti, kivi ja puuklotsiga kehtivad kõikide vooliste korral ja on kokku võetavad Archimedese seaduseks:

Kui keha on osaliselt või täielikult sisestatud voolisesse, mõjub talle ümbritseva voolise poolt üleslükkejõud ${\to F}_{¨ u}$ . See jõud on suunatud vertikaalselt üles ja tema suurus on võrdne keha poolt välja tõrjutud voolise kaaluga $m_{v} g$ .

Kehale mõjuva üleslükkejõu suurus on

(üleslükkejõud, 14-16)

F_{¨ u} = m_{v} g

kus $m_{v}$ on keha poolt välja tõrjutud voolise mass.

Ujumine

Kui vabastame kergest puust klotsi basseinis just veepinna kohal, hakkab klots vette vajuma, kuna raskusjõud tõmbab teda allapoole. Mida enam klots vett välja tõrjub, seda enam kasvab talle mõjuva üleslükkejõu suurus $F_{¨ u}$ . Lõpuks saab $F_{¨ u}$ piisavalt suureks, võrdudes klotsile mõjuva allapoole suunatud raskusjõuga ja klots peatub. Klots on siis staatilises tasakaalus ja öeldakse vees ujuvat. Üldiselt,

Kui keha ujub voolises, siis on talle mõjuva üleslükkejõu suurus $F_{¨ u}$ võrdne kehale mõjuva raskusjõu suurusega $F_{g}$ .

Me võime selle väite kirjutada kujul

(ujumine, 14-17)

F_{¨ u} = F_{g}

Valemist 14-16 teame, et $F_{¨ u} = m_{v} g$ . Seega,

Kui keha ujub voolises, siis on talle mõjuva raskusjõu suurus $F_{g}$ võrdne keha poolt välja tõrjutud voolise kaaluga $m_{v} g$ .

Me võime selle väite kirjutada kujul

(ujumine, 14-18)

F_{g} = m_{v} g

Teisisõnu, ujuv keha tõrjub välja endaga kaalu poolest võrdse voolisehulga.

Näiv kaal voolises

Kui asetame kivi kalibreeritud kaalule, näitab selle lugem kivi kaalu. Kui aga teeme sedasama vee all, vähendab kivile mõjuv üleslükkejõud lugemit. Lugem annab siis näiva kaalu. Üldiselt on näiv kaal seotud keha tegeliku kaaluga kui

(n ¨ a iv kaal) = (tegelik kaal) - (¨ u lesl ¨ u kkej ˜ o u suurus)

mille võime kirjutada kui

(14-19)

{kaal}_{n ¨ a iv} = kaal - F_{¨ u}

Kui peaksite mingil jõuproovil kergitama rasket kivi, suudaksite seda märksa lihtsamini teha vee all oleva kiviga. Siis peaks teie poolt rakendatud jõud suutma ületada vaid kivi näivat kaalu, mitte tema suuremat tegelikku kaalu, sest üleslükkejõud aitaks teil kivi kergitada.

Ujuvale kehale mõjuva üleslükkejõu suurus on võrdne keha kaaluga. Võrrand 14-19 ütleb meile seega, et ujuva keha näiv kaal on null – kaalul saaksime me siis null-lugemi. (Kui astronaudid valmistuvad täitma keerukat ülesannet kosmoses, harjutavad nad seda ülesannet vee all ujudes, kus nende näiv kaal on null nagu kosmoseski.)

Pingviin ujub esmalt vedelikus tihedusega

ρ_{0}

, seejärel vedelikus tihedusega

0, 95 ρ_{0}

ja siis vedelikus tihedusega

1, 1 ρ_{0}

. (a) Järjestage tihedused pingviinile mõjuva üleslükkejõu suuruse järgi suurimast alustades. (b) Järjestage tihedused pingviini poolt välja tõrjutud vedeliku hulga järgi suurimast alustades.

Joonisel 14-11a liugleb surfaja laine esiküljel kohas, kus lainepinna puutuja tõusunurk on

30^{\circ}

. Surfaja ja lainelaua kogumass on

m = 83, 0 k g

ja lainelaua vette sukeldunud osa ruumala on

V = 2, 50 \times 10^{- 2} m^{3}

. Surfaja säilitab laine suhtes oma asendi, kui laine liigub jääva kiirusega kalda poole. Millised on vee poolt lainelauale avaldatava takistusjõu suurus ja suund (joonisel 14-11b kujutatud

x

-telje positiivse suuna suhtes)?

Lahendus

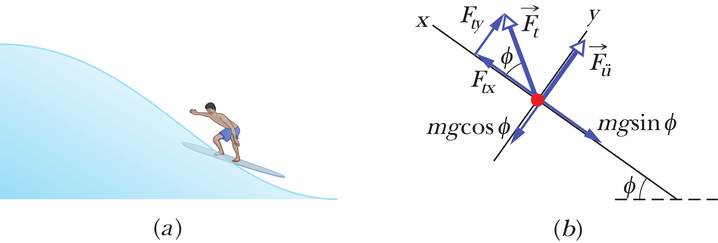
JOONIS 14-11 (a) Surfaja. (b) Surfaja-lainelaua süsteemile mõjuvate jõude vektordiagramm.

JUHTMÕTTED (1) Surfajale mõjuva üleslükkejõu suurus on võrdne lainelaua vette sukeldunud ruumala poolt välja tõrjutud vee kaaluga. Selle jõu suund on risti veepinnaga surfaja asukohas. (2) Kuna surfaja liigub kalda poole ühtlase kiirusega, peab Newtoni teise seaduse kohaselt üleslükkejõu ${\to F}_{¨ u}$ , raskusjõu ${\to F}_{g}$ ja takistusjõu ${\to F}_{t}$ vektorsumma võrduma nulliga.

Arvutused: Jõud ja nende komponendid on näidatud vektordiagrammil joonisel 14-11b. Raskusjõud ${\to F}_{g}$ on suunatud vertikaalselt allapoole (nagu nägime peatükis 5) ja omab komponenti $m g sin θ$ piki kallakut allpoole ning komponenti $m g cos θ$ risti kallakuga. Lainelauale mõjub vee takistusjõud ${\to F}_{t}$ , kuna vett surutakse laine kalda poole liikudes laines pidevalt ülespoole. Seetõttu mõjub lainelaule tõukejõud, mis on suunatud üles- ja tahapoole (kaldast eemale) nurga $ϕ$ all telje $x$ suhtes. Üleslükkejõud ${\to F}_{¨ u}$ on risti veepinnaga, ta suurus sõltub lainelaua poolt välja tõrjutud vee massist, nagu on antud valemiga 14-16 ( $F_{¨ u} = m_{v} g$ ). Valemist 14-2 ( $ρ = m / V$ ) saame me esitada selle massi merevee tiheduse $ρ_{v}$ ja lainelaua sukeldunud ruumala $V$ kaudu: $m_{v} = ρ_{v} V$ . Tabelist 14-1 leiame merevee tiheduse $ρ_{v}$ väärtuseks $1, 024 \times 10^{3} k g / m^{3}$ . Seega on üleslükkejõu suuruseks

F_{¨ u} = m v g = ρ_{w} V g = (1, 024 \times 10^{3} k g / m^{3}) (2, 50 \times 10^{- 2} m^{3}) (9, 8 m / s^{2}) = 2, 509 \times 10^{2} N

Newtoni teine seadus $y$ -telje sihis,

F_{t y} + F_{¨ u} - m g cos θ = m (0)

saab nüüd kuju

F_{t y} + 2, 509 \times 10^{2} N - (83 k g) (9, 8 m / s^{2}) cos 30, 0^{\circ} = 0

mis annab

F_{t y} = 453, 5 N

Newtoni teine seadus ${\to F}_{res} = m \to a$ $x$ -telje sihis,

F_{t x} - m g sin θ = m (0)

annab tulemuseks $F_{t x} = 406, 7 N$ .

Takistusjõu kahest komponendist saame jõu suuruse

F_{d} = \sqrt{(406, 7 N)^{2} + (453, 5 N)^{2}} = 609 N - ---- - - ---- -

ja nurga

ϕ = t a n^{- 1} (\frac{453, 5 N}{406, 7 N}) = 48, 1^{\circ} - ---- - - ---- -

Lainelaual püsimine: kui surfaja kallutab lainelauda pisut ettepoole, kahaneb takistusjõu suurus ja muutub nurk $ϕ$ . Tulemusena pole summaarne jõud enam null ja surfaja liigub mööda lainefronti allapoole. Laskumine on mõneti iseseadistuv, sest surfaja laskudes muutub lainepinna kaldenurk $θ$ väiksemaks ja seega muutub väiksemaks ka raskusjõu komponent $m g sin θ$ , mis surfajat kallakust alla tõmbab. Seega saab surfaja juhtida lauda, saavutamaks uut tasakaalu juba allpool. Sarnaselt, kallutades lauda veidi tahapoole, suurendab surfaja takistusjõudu ja liigub mööda lainefronti üles. Kui surfaja on veel laine madalamas osas, siis $θ$ ja $m g sin θ$ mõlemad kasvavad ning surfaja saab jällegi valitseda mõjuvaid jõude ja saavutada tasakaalu.

Näidisülesanne 14-5

JOONIS 14-12 Klots kõrgusega $H$ ujub vedelikus, olles sukeldunud sügavuseni $h$ .

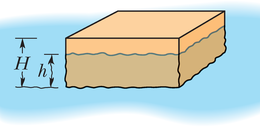
Joonisel 14-12 ujub klots tihedusega $ρ = 800 k g / m^{3}$ vedelikus tihedusega $ρ_{v} = 1200 k g / m^{3}$ . Klotsi kõrgus on $H = 6, 0 c m$ .

Millise sügavuseni

h

istub klots vedelikus?

Lahendus

JUHTMÕTE (1) Ujumine nõuab, et ülespoole suunatud üleslükkejõud tasakaalustaks klotsile mõjuva allapoole suunatud raskusjõu. (2) Üleslükkejõud on võrdne klotsi vedelikku sukeldunud osa poolt välja tõrjutud vedeliku kaaluga $m_{v} g$ .

Arvutused: Valemist 14-16 teame, et üleslükkejõu suurus on $F_{¨ u} = m_{v} g$ , kus $m_{v}$ on klotsi sukeldunud osa ruumala $V_{v}$ poolt välja tõrjutud vedeliku mass. Valemist 14-2 ( $ρ = m / V$ ) teame, et väljatõrjutud vedeliku mass $m v = ρ_{v} V_{v}$ . Me ei tea suurust $V_{v}$ , aga kui tähistame klotsi horisontaalse tahu pikkuse ja laiuse vastavalt $L$ ja $W$ , siis näeme jooniselt 14-12, et klotsi sukeldunud osa ruumala on $V_{v} = L W h$ . Kui kombineerime nüüd meie kolm valemit, saame üleslükkejõu suuruseks

(14-20)

F_{¨ u} = m_{v} g = ρ_{v} V_{v} g = ρ_{v} L W h g

Sarnaselt võime kirjutada välja klotsile mõjuva raskusjõu $F_{g}$ esmalt klotsi massi $m$ kaudu, siis klotsi tiheduse $ρ$ ja (täis)ruumala $V$ kaudu ja seejärel kasutades klotsi mõõtmeid $L$ , $W$ ja $H$ (täiskõrgus):

(14-21)

F_{g} = m g = ρ V g = ρ L W H g

Ujuv klots on tasakaalus. Kirjutades välja Newtoni teise seaduse vertikaaltelje $y$ suunaliste jõukomponentide jaoks ( $F_{res, y} = m_{a y}$ ), saame

F_{¨ u} - F_{g} = m (0)

ehk valemitest 14-20 ja 14-21

ρ_{v} L W h g - ρ L W H g = 0

mis annab meile

h = \frac{ρ}{ρ_{v}} H = \frac{800 k g / m^{3}}{1200 k g / m^{3}} (6 c m) = 4 c m - --- - - --- -

Kui klots uputatakse täielikult ja lastakse seejärel lahti, siis kui suure kiirendusega hakkab ta liikuma?

Lahendus

Arvutused: Klotsile mõjuv raskusjõud on sama, aga täielikult sukeldatud klotsi korral on väljatõrjutud vee ruumala $V = L W H$ . (Kasutatud on klotsi täiskõrgust.) See tähendab, et $F_{¨ u}$ väärtus on nüüd suurem ja klots pole enam tasakaalus, vaid hakkab kiirenevalt ülespoole liikuma. Newtoni teine seadus annab

F_{¨ u} - F_{g} = m a

ehk

ρ_{v} L W H g - ρ L W H g = ρ L W H a

kus me asendasime klotsi massi $m$ väärtuseks $ρ L W H$ . Lahendamine $a$ suhtes annab

a = (\frac{ρ_{v}}{ρ} - 1) g = (\frac{1200 k g / m^{3}}{800 k g / m^{3}} - 1) (9, 8 m / s^{2}) = 4, 9 m / s^{2} - -------- - - -------- -

Ideaalsete vooliste liikumine

JOONIS 14-13 Teatud kohas muutub suitsu ja kuuma gaasi tõusev vool statsionaarsest turbulentseks. (Will McIntyre / Photo Researchers)

Reaalsete vooliste liikumine on väga keerukas ja täielikult seda veel ei mõisteta. Selle asemel vaatleme me ideaalse voolise liikumist, mida on matemaatiliselt lihtsam käsitleda, aga mis siiski annab kasulikke tulemusi. Järgnevad on neli eeldust, mida me teeme oma ideaalse voolise kohta, nad kõik puudutavad voolamist:

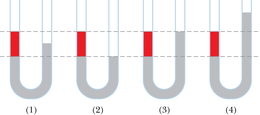
Statsionaarne voolamine Statsionaarsel (ehk laminaarsel) voolamisel ei muutu liikuva voolise kiirus üheski punktis ei suuruse ega suuna poolest. Tasane veevool vaikse hoovuse keskel on statsionaarne, vool kärestike kaskaadis ei ole. Joonis 14-13 näitab üleminekut statsionaarselt voolamiselt mittestatsionaarsele (ehk mittelaminaarsele ehk turbulentsele) voolamisele tõusvas suitsujoas. Suitsuosakeste kiirus kasvab tõustes ja teatud kriitilisel kiirusel muutub voolamine statsionaarsest mittestatsionaarseks.
Kokkusurumatu vool Nagu liikumatute vooliste korralgi, eeldame me, et meie ideaalne voolis on kokkusurumatu; s.t et ta tihedusel on ühtlane konstantne väärtus.
Mitteviskoosne voolamine Laias laastus on voolise viskoossus tema vastupanu mõõt voolamisele. Näiteks avaldab paks mesi voolamisele enam vastupanu kui vesi ja nii öeldakse, et mesi on viskoossem kui vesi. Viskoossus on tahkiste vahelise hõõrde analoog; mõlemad on mehhanismid, mille kaudu liikuvate objektide kineetiline energia muundub soojuseks. Hõõrde puudumisel võib klots libiseda konstantse kiirusega mööda horisontaalset pinda. Samamoodi ei kohta objekt, mis liigub läbi mitteviskoosse voolise, viskoosset takistusjõudu – s.t viskoossusest põhjustatud vastupanujõudu; see võib liikuda läbi voolise konstantse kiirusega. Inglise teadlane Lord Rayleigh märkis, et ideaalses voolises laevakruvi ei töötaks, teisalt ei vajakski laev (kui kord juba liikuma pandud) seal üldse kruvi!
Keerisvaba voolamine Kuigi see meid edasises ei puuduta, eeldame samuti, et voolamine on keerisvaba. Selle omaduse kontrollimiseks jälgime koos vedelikuga liikuvat väikest tolmukübet. Kuigi see proovikeha võib (või võib ka mitte) liikuda ringikujulisel trajektooril, ei pöörle keerisvabas voolus keha ümber oma masskeset läbiva telje. Ligikaudse analoogiana võib lõbustuspargi suure vaateratta liikumist vaadelda keerisliikumisena, gondlites istujate liikumine on aga keerisvaba.

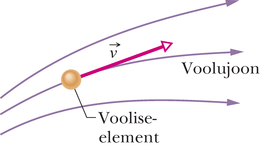
JOONIS 14-14 Voolise statsionaarne voolamine ümber silindri, tehtud nähtavaks silindrist ülesvoolu sisestatud värvtrasseerija abil. (Avaldatud D. H. Peregrine’i (University of Bristol) loal)

JOONIS 14-15 Vooliseelement trasseerib oma liikumisel voolujoont. Elemendi kiirusvektor on voolujoone igas punktis voolujoone puutujaks.

Voolise voolamist saab muuta nähtavaks trasseerija lisamisega. Selleks võib olla värv, mida viiakse voolisejoa paljudesse punktidesse (joonis 14-14), või gaasivoolule lisatud suitsuosakesed (joonis 14-13). Trasseerija iga osake järgib voolujoont – nii nimetatakse trajektoori, mida voolamisel läbib väike vooliseelement. Meenutame peatükist 4, et osakese kiirus on alati tema trajektoori puutujaks. Siin on osakeseks vooliseelement ja selle kiirus $\to v$ on alati voolujoone puutujaks (joonis 14-15). Sel põhjusel ei saa kaks voolujoont kunagi lõikuda: kui nad seda teeksid, siis peaks nende lõikepunkti jõudev vooliseelement omama kahte kiirust korraga, mis on võimatu.

Pidevuse võrrand

Küllap olete märganud, et saate suurendada kastmisvoolikust väljuva veejoa kiirust, sulgedes pöidlaga osaliselt vooliku avause. Ilmselt sõltub vee kiirus $v$ ristlõike pindalast $A$ , läbi mille vesi voolab.

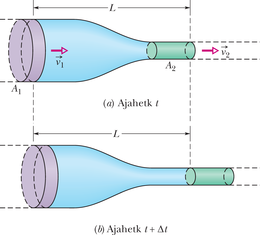
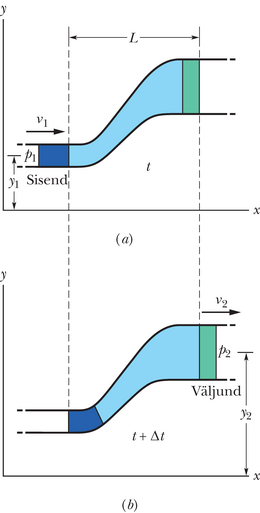
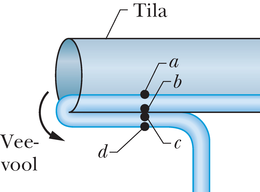
JOONIS 14-16 Voolise kiirus vasakus otsas on $v_{1}$ , paremas otsas $v_{2}$ . Toru ristlõike pindala vasakus otsas on $A_{1}$ , paremas $A_{2}$ . Ajahetkest $t$ (a) kuni ajahetkeni $t + Δ t$ (b) siseneb vasakult torusse lillaks värvitud voolisehulk ja sama suur roheliseks värvitud voolisehulk väljub toru paremast otsast.

Tuletame nüüd seose $v$ ja $A$ vahel statsionaarsel voolamisel muutuva ristlõikega torus, nagu kujutatud joonisel 14-16. Vool kulgeb seal vasakult paremale ja kujutatud torulõigu (moodustab osa pikemast torust) pikkus on $L$ . Voolise kiirus on $v_{1}$ vasakus otsas ja $v_{2}$ paremas otsas. Toru ristlõike pindala vasakus otsas on $A_{1}$ , paremas $A_{2}$ . Oletame, et ajavahemikus $Δ t$ siseneb vasakult torulõiku voolisekogus ruumalaga $Δ V$ (joonisel 14-16 värvitud lillaks). Kuna voolis on kokkusurumatu, siis peab torulõigu vasakust otsast väljuma sama vooliseruumala $Δ V$ (joonisel 14-16 värvitud roheliseks).

JOONIS 14-17 (a) Ajahetkel $t$ on vooliseelement $e$ läbimas punktiirjoont. (b) Ajahetkel $t + Δ t$ on sama element $e$ kaugusel $Δ x = v Δ t$ punktiirjoonest.

Kiiruste ja ristlõigete seostamiseks saame me kasutada seda ühist ruumala $Δ V$ b ühtlase ristlõikega $A$ toru külgvaadet. Joonisel 14-17a on vooliseelement e läbimas toruga ristuvat punktiirjoont. Elemendi kiirus on $v$ , seega läbib ta aja $Δ t$ jooksul piki toru vahemaa $Δ x = v Δ t$ . Voolise ruumala $Δ V$ , mis läbib aja $Δ t$ jooksul punktiirjoont, avaldub kujul

(14-22)

Δ V = A Δ x = A v Δ t

Rakendades seost 14-22 joonisel 14-16 kujutatud torulõigu vasakule ja paremale otsale, saame

Δ V = A_{1} v_{1} Δ t = A_{2} v_{2} Δ t

ehk

(pidevuse võrrand, 14-23)

A_{1} v_{1} = A_{2} v_{2}

Seda seost kiiruse ja ristlõike pindala vahel kutsutakse pidevuse võrrandiks ideaalse voolise voolamise jaoks. Ta ütleb meile, et voolukiirus kasvab, kui me kahandame ristlõike pindala, läbi mille voolis voolab (nagu siis, kui sulgeme pöidlaga osa kastmisvooliku otsast).

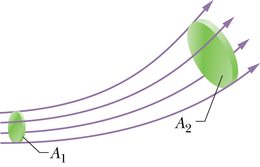
JOONIS 14-18 Voolutoru on määratud voolujoontega, mis moodustavad ta seina. Voolu ruumkiirus peab olema sama voolutoru kõigi ristlõigete jaoks.

Võrrand 14-23 rakendub mitte ainult reaalsele torule, vaid ka suvalisele nn voolutorule ehk kujutletavale torule, mille sein koosneb voolujoontest. Selline konstruktsioon toimib reaalse toruna, kuna ükski vooliseelement ei saa ületada voolujoont; seega peab kogu voolis voolutorus jääma selle piiridesse. Joonis 14-18 kujutab voolutoru, milles ristlõike pindala kasvab voolu suunas väärtusest $A_{1}$ väärtuseni $A_{2}$ . Võrrandist 14-23 teame, et pindala kasvamisega peab kiirus kahanema, mida näitab voolujoonte suurem vahekaugus joonisel 14-18 paremal. Sarnaselt võite joonisel 14-14 näha, et voolukiirus on suurim just silindri kohal ja all.

Võrrandi 14-23 võime ümber kirjutada kujul

(voolu ruumkiirus, pidevuse võrrand, 14-24)

R_{r} = A_{v} = const

kus $R_{r}$ on voolu ruumkiirus (ajaühikus antud kohast mööduva voolise ruumala). Selle ühikuks SI-süsteemis on kuupmeeter sekundis ( $m^{3} / s$ ). Kui voolise tihedus $ρ$ on ühtlane, võime me võrrandi 14-24 selle tihedusega läbi korrutada ja saada massi voolukiiruse (mass ajaühikus):

(massi voolukiirus, 14-25)

R_{m} = ρ R_{r} = ρ A_{v} = const

SI ühik massi voolukiiruse jaoks on kilogramm sekundis ( $k g / s$ ). Võrrand 14-25 ütleb, et mass, mis voolab igas sekundis joonisel 14-16 kujutatud torulõiku sisse, peab võrduma massiga, mis voolab samast torulõigust igas sekundis välja.

Joonisel on kujutatud torustik ning toodud voolude ruumkiirused (

c m^{3} / s

) ja suunad kõikides torudes, üks välja arvatud. Milline on voolu ruumkiirus ja suund selles torus?

Joonis 14-19 näitab, kuidas kraanist väljuv veejuga langedes kitseneb. Näidatud ristlõigete pindalad on

A_{0} = 1, 2 c m^{2}

A = 0, 35 c m^{2}

. Vastavate tasemete vertikaalne vahemaa on

45 m m

. Milline on kraanist väljuva vee ruumkiirus?

Lahendus

JOONIS 14-19 Kraanist väljuva vee langemisel ta kiirus kasvab. Kuna voolu ruumkiirus peab olema sama kõigis joa horisontaalsetes ristlõigetes, siis peab juga kitsenema.

JUHTMÕTE Voolu ruumkiirus läbi kõrgema ristlõike peab olema sama mis läbi madalama.

Arvutused: Võrrandist 14-24 saame

A_{0} v_{0} = A_{v}

kus $v_{0}$ ja $v$ on vee kiirused ristlõigetele $A_{0}$ ja $A$ vastavatel tasemetel. Kuna vesi langeb vabalt kiirendusega $g$ , saame võrrandist 2-16

v^{2} = v_{0}^{2} + 2 g h

Avaldades võrrandist 14-26

v

, asetades selle võrrandisse 14-27 ja lahendades saadud võrrandi

v_{0}

suhtes, saame

v_{0} = \sqrt{\frac{2 g h A_{0}}{A_{0}^{2} - A^{2}}} = \sqrt{\frac{(2) (9, 8 m / s^{2}) (0, 045 m) (0, 35 c m^{2})}{(1, 2 c m^{2})^{2} (0, 35 c m^{2})^{2}}} = 0, 286 m / s = 28, 6 m / s

Võrrandist 14-24 saame voolu ruumkiiruse

R_{r} = A_{0} v_{0} = (1, 2 c m^{2}) (28, 6 c m / s) = 34 c m^{3} / s - -------- - - -------- -

Bernoulli võrrand

JOONIS 14-20 Voolis voolab statsionaarselt läbi torupikkuse $L$ , sisendist vasakult kuni väljundini paremal. Hetkest $t$ joonisel (a) kuni hetkeni $t + Δ t$ joonisel (b) siseneb torusse tumesiniseks värvitud voolisekogus ja väljub roheliseks värvitud voolisekogus.

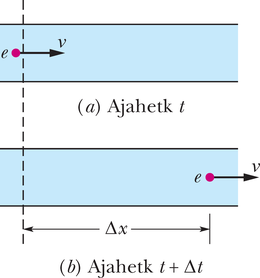
Joonisel 14-20 on kujutatud toru, mida mööda voolab statsionaarse kiirusega ideaalne voolis. Oletame, et ajavahemiku $Δ t$ jooksul siseneb torusse vasakpoolsest otsast (sisendist) voolise ruumala $Δ V$ , joonisel 14-20 värvitud violetseks, ja sama suur ruumala, joonisel 14-20 värvitud roheliseks, väljub toru parempoolsest otsast (väljundist). Väljuv ruumala peab olema niisama suur kui sisenev, kuna voolis on eeldatavasti kokkusurumatu ja konstantse tihedusega $ρ$ .

Olgu $y_{1}$ , $v_{1}$ ja $p_{1}$ vasakult siseneva voolise kõrgus, kiirus ja rõhk ning $y_{2}$ , $v_{2}$ ja $p_{2}$ samad suurused paremalt väljuva voolise jaoks. Rakendades voolisele energia jäävuse seadust näitame, et nende suuruste vahel kehtib seos

(14-28)

p_{1} + \frac{1}{2} ρ v_{1}^{2} + ρ g y_{1} = p_{2} + \frac{1}{2} ρ v_{2}^{2} + ρ g y_{2}

Üldiselt kutsutakse liiget $\frac{1}{2} ρ v^{2}$ voolise kineetilise energia tiheduseks (kineetiline energia ruumalaühiku kohta). Võrrandi 14-28 võime esitada ka kujul

(Bernoulli võrrand, 14-29)

p + \frac{1}{2} ρ v^{2} + ρ g y = const

Võrrandid 14-28 ja 14-29 on Bernoulli võrrandi ekvivalentsed kujud, saanud nime Daniel Bernoulli järgi, kes uuris vooliste voolamist 18. sajandil.* Sarnaselt pidevuse võrrandile (valem 14-24) pole ka Bernoulli võrrand uus seadus, vaid lihtsalt tuntud põhimõtete sobivam ümbersõnastus vooliste mehhaanika jaoks. Kontrollimiseks rakendame Bernoulli võrrandit paigalseisvatele voolistele, võttes võrrandis 14-28 $v_{1} = v_{2} = 0$ . Tulemuseks on

p_{2} = p_{2} + ρ g (y_{1} - y_{2})

s.o võrrand 14-7.

Olulise järelduse Bernoulli võrrandist saame, kui võtame $y$ konstantseks (näiteks $y = 0$ ), nii et voolise kõrgus voolamisel ei muutu. Võrrand 14-28 saab siis kuju

(14-30)

p_{1} + \frac{1}{2} ρ v_{1}^{2} = p_{2} + \frac{1}{2} ρ v_{2}^{2}

mis ütleb meile:

Kui piki horisontaalset voolujoont liikuva vooliseelemendi kiirus kasvab, siis peab rõhk voolises kahanema ja vastupidi.

Ehk teisiti: seal, kus voolujooned on üksteisele suhteliselt lähedal (kus kiirus on suhteliselt suur), on rõhk suhteliselt madal ja vastupidi.

Seos kiiruse muutuse ja rõhu muutuse vahel omab mõtet ka siis, kui te vaatlete ühte vooliseelementi. Kui selline element läheneb voolutoru kitsale piirkonnale, siis suurem rõhk elemendi taga kiirendab teda, nii et selles kitsas piirkonnas on tal suurem kiirus. Kui ta läheneb laiemale piirkonnale, siis suurem rõhk vooliseelemendi ees aeglustab teda, nii et tal saab laias piirkonnas olema väiksem kiirus.

Bernoulli võrrand kehtib täpselt ainult sel määral, mil vedelik on ideaalne. Kui on olemas viskoossusjõud, tuleb mängu ka soojusenergia. Me ei arvesta seda järgnevas tuletuskäigus.

Bernoulli võrrandi tõestus

Võtame oma süsteemiks (ideaalse) voolise kogu joonisel 14-20 kujutatud ruumalas. Me rakendame sellele süsteemile energia jäävuse seadust tema liikumisel algolekust (joonis 14-20a) lõppolekusse (joonis 14-20b). Voolis, mis jääb joonisel 14-20 vahemaaga $L$ eraldatud kahe vertikaalse tasapinna vahele, ei muuda selle protsessi käigus oma olekut, seega peame tähele panema vaid muutusi, mis leiavad aset sisend- ja väljundotste juures.

Esmalt rakendame energia jäävust töö ja kineetilise energia teoreemi kujul

(14-31)

W = Δ K

mis ütleb meile, et süsteemi kineetilise energia muut peab olema võrdne süsteemi kallal tehtud kogutööga. Kineetilise energia muut tuleneb kiiruste erinevusest toru otstes ja on

(14-32)

Δ K = \frac{1}{2} Δ m v_{2}^{2} - \frac{1}{2} Δ m v_{1}^{2} = \frac{1}{2} ρ Δ V (v_{2}^{2} - v_{1}^{2})

kus $Δ m$ ( $= ρ Δ V$ ) on vedeliku mass, mis siseneb torusse sisendist ja väljub väljundist lühikese ajavahemiku $Δ t$ jooksul.

Süsteemi kallal tehtud töö tuleneb kahest allikast. Raskujõu ( $Δ m \to g$ ) töö $W_{g}$ massiga $Δ m$ voolise tõstmiseks lähtenivoolt lõppnivoole on

(14-33)

W_{g} = - Δ m g (y_{2} - y_{1}) = - ρ g Δ V (y_{2} - y_{1})

See töö on negatiivne, kuna ülespoole suunatud vertikaalse nihke ja allapoole suunatud raskusjõu suunad on vastupidised.

Samuti tuleb tööd teha süsteemi kallal (sisendis) surumaks sisenevat voolist torusse, ja süsteemi poolt (väljundis) surumaks edasi voolist, mis asub väljuva voolise ees. Üldiselt avaldub töö, mida teeb jõud suurusega $F$ selleks, et suruda torus olevat vooliseosa pindalaga $A$ edasi vahemaa $Δ x$ võrra, kujul

F Δ x = (p A) (Δ x) = p (A Δ x) = p Δ V

Süsteemi kallal tehtud töö on siis $p_{1} Δ V$ ja süsteemi poolt tehtud töö $- p_{2} Δ V$ . Nende summa $W_{p}$ on

(14-34)

W_{p} = - p_{2} Δ V + p_{1} Δ V = - (p_{2} - p_{1}) Δ V

Töö ja kineetilise energia teoreem (valem 14-31) saab nüüd kuju

W = W_{g} + W_{p} = Δ K

Asendused võrranditest 14-32, 14-33 ja 14-34 annavad

- ρ g Δ V (y_{2} - y_{1}) - Δ V (p_{2} - p_{1}) = \frac{1}{2} ρ Δ V (v_{2}^{2} - v_{1}^{2})

Viimane tulemus ühtib pärast lihtsaid teisendusi valemiga 14-28, mille tõestamine oligi meie eesmärgiks.

Vesi voolab laminaarselt läbi joonisel kujutatud toru allapoole. Järjestage neli nummerdatud torulõiku (a) neis oleva voolu ruumkiirguse

R_{r}

järgi, (b) neis oleva voolu kiiruse

v

järgi, (c) neis oleva vee rõhu

p

järgi, suurimast väärtusest alustades.

Etanool tihedusega

ρ = 791 k g / m^{3}

voolab laminaarselt läbi horisontaalse toru, mis aheneb (nagu joonisel 14-16) ristlõikest

A_{1} = 1, 20 \times 10^{- 3} m^{2}

ristlõikeni

A_{2} = A_{1} / 2

. Rõhkude erinevus toru laia ja kitsa osa vahel on

4120 P a

. Kui suur on etanooli voolamise ruumkiirus

R_{r}

Lahendus

JUHTMÕTTED (1) Kuna toru jämedamat osa läbiv vedelik läbib täielikult ka kitsa osa, peab voolamise ruumkiirus $R_{r}$ olema toruosades sama. Seega võrrandist 14-24

(14-35)

R_{r} = v_{1} A_{1} = v_{2} A_{2}

Paraku sisaldab see kahte tundmatut kiirust, mistõttu me ei saa siit leida $R_{r}$ väärtust. (2) Kuna voolamine on laminaarne, võime me rakendada Bernoulli võrrandit. Valemist 14-28 saame

(14-36)

p_{1} + \frac{1}{2} ρ v_{1}^{2} + ρ g y = p_{2} + \frac{1}{2} ρ v_{2}^{2} + ρ g y

kus alaindeksid $1$ ja $2$ viitavad vastavalt toru jämedamale ja kitsamale osale ja $y$ on nende ühine kõrgus. Ka sellest võrrandist ei näi otsest abi tõusvat, sest ta ei sisalda otsitavat suurust $R_{r}$ ja sisaldab kahte tundmatut kiirust $v_{1}$ ja $v_{2}$ .

Arvutused: On olemas kaval tee võrrandi 14-36 töölerakendamiseks. Esmalt võime me kasutada võrrandit 14-36 ja fakti, et $A_{2} = A_{1} / 2$ , ja kirjutada

(14-37)

v_{1} = \frac{R_{r}}{A_{1}} ja v_{2} = \frac{R_{r}}{A_{2}} = \frac{2 R_{r}}{A_{1}}

Seejärel võime asetada need avaldised valemisse 14-36, millega elimineerime tundmatud kiirused ja toome sisse otsitava ruumkiiruse. Nii tehes ja lahendades saadud võrrandi $R_{r}$ suhtes, saame

(14-38)

R_{r} = A_{1} \sqrt{\frac{2 (p_{1} - p_{2})}{3 ρ}}

Üks küsimus tuleb meil siiski veel lahendada: me teame, et rõhkude erinevus kahe osa vahel on $4210 P a$ , aga kas see tähendab, et $p_{1} - p_{2} = 4120 P a$ või $- 4210 P a$ ? Me võime oletada, et esimene variant on õige, vastasel juhul annaks ruutjuur valemis 14-38 meile imaginaararvulise tulemuse. Püüame aga oletamise asemel kasutada arutlust. Valemist 14-35 näeme me, et kiirus $v_{2}$ toru kitsas osas (väike $A_{2}$ ) peab olema suurem kui kiirus $v_{2}$ toru jämedamas osas (suur $A_{1}$ ). Meenutame, et kui voolise kiirus kasvab horisontaalsel liikumisel (nagu siin), peab voolise rõhk kahanema. Seega on $p_{1}$ suurem kui $p_{2}$ ja $p_{2} - p_{1} = 4120 P a$ . Asetades selle ja teised teadaolevad andmed valemisse 14-38, saame

R_{V} = 1, 20 \times 10^{- 3} m^{3} \sqrt{\frac{(2) (4120 P a)}{(3) (791 k g / m^{3}}} = 2, 24 \times 10^{- 3} m^{3} / s - ----------------- - - ----------------- -

Metsikus Läänes tulistas bandiit kaanetamata veepaaki (joonis 14-21), tekitades augu veepinnast allpool kaugusel

h

. Millise kiirusega hakkas vesi paagist välja voolama?

Lahendus

JOONIS 14-21 Vesi voolab läbi veepaagis oleva ava sügavusel $h$ allpool veepinda. Rõhk veepinnal ja augu juures on atmosfäärirõhk $p_{0}$ .

JUHTMÕTTED (1) Situatsioon on põhimõttelt sama nagu juhul, kui vesi liiguks kiirusega $v_{0}$ (allapoole) läbi jämeda toru (paak) ristlõikega $A$ ja seejärel liiguks (horisontaalselt) kiirusega $v$ läbi kitsa toru (auk) ristlõikega $a$ . (2) Kuna vesi, mis voolab läbi jämeda toru, peab täielikult mahtuma ka läbi kitsa toru, peab voolu ruumkiirus olema mõlemas „torus” sama. (3) Me võime samuti siduda $v$ ja $v_{0}$ (ja h) Bernoulli võrrandi (valem 14-28) abil.

Arvutused: Valemist 14-24

R_{r} = a v = A v_{0}

ja seega

v_{0} = \frac{a}{A} v

Kuna $a ≪ A$ , näeme, et $v_{0} ≪ v$ . Bernoulli võrrandi rakendamiseks võtame augu nivoo kõrguste (ja seega ka gravitatsiooni energia) arvutamisel tuginivooks. Pannes tähele, et rõhk veepinna kohal paagis ja kuuliaugu juures on atmosfäärirõhk $p_{0}$ (mõlemad kohad on atmosfäärile avatud), kirjutame võrrandi 14-28 kujul

(14-39)

p_{0} + \frac{1}{2} ρ v_{0}^{2} + ρ g h = p_{0} + \frac{1}{2} ρ v^{2} + ρ g (0)

(Siin kirjeldab veepinda paagis võrrandi vasak pool ja auku võrrandi parem pool. Null paremal viitab, et auk asub meie tuginivool.) Enne kui asume võrrandit 14-39 $v$ suhtes lahendama, võime kasutada oma tulemust $v_{0} ≪ v$ tema lihtsustamiseks: Me eeldame, et $v_{0}^{2}$ ja seega ka liige $\frac{1}{2} ρ v_{0}^{2}$ võrrandis 14-39 on teiste liikmetega võrreldes tühine, mistõttu võime ta välja jätta. Järelejäänud võrrandi lahendamine annab

v = \sqrt{2 g h} - ----- - - ----- -

See on sama kiirus, mille omandaks ese kõrguselt $h$ paigalseisust kukkudes.

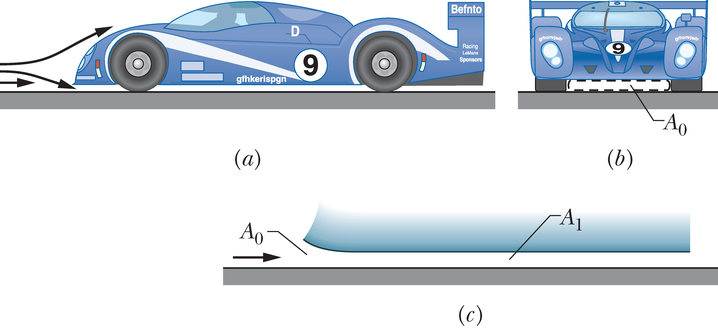
Näidisülesanne 14-9 Arenda oma oskusi

Mitut tüüpi võidusõiduautod sõltuvad negatiivsest tõstest (ehk allasurvejõust), mis surub neid vastu rajapinda ja võimaldab kurvide kiiret läbimist vastu rajapiirdeid paiskumata. Osa negatiivsest tõstest on pinnajõud, mis on tingitud autoalusest õhuvoolust. Kui joonisel 14-22a kujutatud võidusõiduauto liigub edasi kiirusega $27, 25 m / s$ , on õhk sunnitud voolama auto alt läbi ja auto kohalt üle (joonis 14-22a). Õhk, mis on sunnitud voolama auto alt läbi, siseneb auto eest läbi pinna ristlõikega $A_{0} = 0, 0330 m^{2}$ (joonis 14-22b) ja voolab seejärel auto all, kus vertikaalse ristlõike pindala $A_{1} = 0, 0310 m^{2}$ . Käsitlege seda õhuvoolu kui statsionaarset voolu läbi horisontaalse toru, mille ristlõige kahaneb väärtusest $A_{1}$ väärtuseni $A_{2}$ (joonis 14-22c).

JOONIS 14-22 (a) Õhk voolab võidusõiduauto kohalt üle ja selle alt läbi. (b) Auto alt läbi voolav õhk siseneb läbi pinna vertikaalse ristlõikega $A_{0}$ . (c) Seejärel koondub vool nagu torus, mille vertikaalne ristlõikepind kahaneb väärtuseni $A_{1}$ .

Hetkel kui õhk läbib pinda

A_{0}

, on ta rõhk võrdne atmosfäärirõhuga

p_{0}

. Millisel rõhul

p_{1}

on õhk pinda

A_{1}

läbides?

Lahendus

JUHTMÕTTED (1) Kuna voolamine on statsionaarne, võime me õhuvoolule rakendada Bernoulli võrrandit (valem 14-28). Kooskõlas sissetoodud indeksitega kirjutame võrrandi kujul

(14-40)

p_{0} + \frac{1}{2} ρ v_{0}^{2} + ρ g y = p_{1} + \frac{1}{2} ρ v_{1}^{2} + ρ g y

kus $ρ$ on õhu tihedus ja $y$ on voolava õhu kõrgus maapinnast. (2) Kuna kogu õhk, mis siseneb läbi pinna ristlõikega $A_{0}$ , peab läbima ka pinna ristlõikega $A_{1}$ , peab voolu ruumkiirus $R_{r}$ läbi nende kahe pinna olema sama.

Arvutused: Valemist 14-24 saame

A_{0} v_{0} = A_{1} v_{1}

ehk

(14-41)

v_{1} = v_{0} \frac{A_{0}}{A_{1}}

Asetame valemi 14-41 valemisse 14-40 ja teisendame, saame

(14-42)

p_{1} = p_{0} - \frac{1}{2} ρ v_{0}^{2} (\frac{A_{0}^{2}}{A_{1}^{2}} - 1)

Õhu kiirus sisenemisel läbi $A_{0}$ auto esiotsas on $27, 25 m / s$ , see on auto kiirus edasiliikumisel läbi õhu. Asetades selle kiiruse, õhu tiheduse $ρ = 1, 21 k g / m^{3}$ ja $A_{0}$ ning $A_{1}$ väärtused valemisse 14-42, leiame

p_{1} = p_{0} - \frac{1}{2} (1, 21 k g / m^{3}) (27, 25 m / s)^{2} (\frac{(0, 0330 m^{2})^{2}}{(0, 0310 m^{2})^{2}} - 1) = p_{0} - 59, 838 P a \approx p_{0} - 59, 8 P a - ------------ - - ------------ -

Seega on õhurõhk auto all $59, 8 P a$ võrra väiksem atmosfäärirõhust.

Kui auto horisontaalne ristlõikepindala on

A_{h} = 4, 86 m^{2}

, milline on siis autole tema all ja peal oleva õhu rõhkude tõttu mõjuva summaarse jõu vertikaalkomponent

F_{r e s, y}

Lahendus

JUHTMÕTE Pinnale mõjuv rõhk on jõud pinnaühiku kohta, nagu antud valemiga 14-4 ( $p = F / A$ ).

Arvutused: Meid huvitavad siin auto põhi ja katus, võtame mõlema pindala võrdseks suurusega $A_{h}$ . Auto kohal on õhk atmosfäärirõhul ja surub autot allapoole vertikaalse jõukomponendiga

F_{y, p e a l} = - p_{0} A_{h}

Auto all on õhurõhk $p_{1} = p_{0} - 59, 838 P a$ ja see surub autot ülespoole vertikaalse jõukomponendiga

F_{y, a l l} = (p_{0} - 59, 838 P a) A_{h}

Summaarne vertikaalne jõukomponent on siis

F_{r e s, y} = F_{y, a l l} + F_{y, p e a l} = (p_{0} - 59, 838 P a) A_{h} - p_{0} A_{h} = - (59, 838 P a) (4, 86 m^{2}) = - 291 N - ------ - - ------ -

Teise auto tuules kihutamisega seotud oht: summaarne allasuunatud jõud, mis on tingitud kahanenud õhurõhust auto all (pinnaefekt), moodustab $30 %$ kogu negatiivsest tõstest, mis aitab autot rajal hoida. Ilma negatiivse tõsteta peaks auto kurvides sõitu tugevasti aeglustama, muidu libiseks ta välimisse rajapiirdesse. Võistluste ajal võib juht kahandada autole mõjuvat õhutakistust, järgnedes tihedalt teisele autole – võtab end eelkihutaja tuulde. Vedav auto katkestab aga pideva õhuvoolu jälitava auto all ja kaotab selle jaoks pinnaefekti. Kui jälitav juht ei oota seda kadumist ja ei aeglusta vastavalt sõitu, võib libisemine rajapiirdesse olla vältimatu.

Summary

Materjali tihedus on defineeritud kui materjali mass ruumalaühiku kohta:

ρ = \frac{Δ m}{Δ V}

Kui materjalinäidis on väga palju suurem aatomite mõõtmetest, võib valemi 14-1 kirjutada kujul

ρ = \frac{m}{V}

Voolis on aine, mis on võimeline voolama; ta võtab oma mahuti kuju, kuna ei suuda vastu panna nihkepingele. Kuid ta võib avaldada oma pinnaga risti olevat jõudu. Seda jõudu iseloomustab rõhk $p$ :

p = \frac{Δ F}{Δ A}

kus $\Delta

Rõhk paigalseisvas voolises muutub sõltuvalt vertikaalsest asukohast $y$ . Kui $y$ positiivne suund on üles, siis

p_{2} = p_{1} + ρ g (y_{1} - y_{2})

Rõhk voolises on sama kõikides samal kõrgusnivool asuvates punktides. Kui $h$ on sügavus voolises arvestatun

Suletud mahutis olevas voolises tekitatud rõhumuutus antakse kahanemata edasi voolise kõikidele osadele ja mahuti seintele.

Kui keha on täielikult või osaliselt sukeldatud voolisesse, siis mõjub kehale ümbritseva voolise poolt üleslükkejõud ${\to F}_{¨ u}$ . See jõud on suunatud vertikaalselt üles ja ta suurus on

F_{¨ u} = m_{v} g

kus $m_{v}$ on keh

Ideaalne voolis on kokkusurumatu ja tal puudub viskoossus, ta voolamine on statsionaarne ja keerisvaba. Voolujoon on trajektoor, mida järgib üksik vooliseosake. Voolutoru on voolujoonte kimp. Voolamisel voolutorus on täidetud pidevuse v&ot

Bernoulli võrrand

Mehaanilise energia jäävuse seaduse rakendamine ideaalse vedeliku voolamisele annab Bernoulli võrrandi:

$p + \frac{1}{2} ρ v^{2} + ρ g y = const$

piki iga voolutoru.

Küsimused

Teekannu efekt. Teekannu tilast aeglaselt välja kallatav vesi võib „kleepuda” tila alla ja voolata seda mööda mõnevõrra tagasi, enne kui tilast irdub ja alla langeb. (Veekihti hoiab tila küljes õhurõhk.) Joonisel 14-23 on veekihis tila sees punkt $a$ veekihi pinnal ja punkt $b$ selle põhjas ning veekihis tila all on punkt $c$ ülal (vastu tila) ja $d$ veekihi alumisel pinnal. Järjesta need punktid manomeetrilise rõhu järgi vees, positiivseimast alustades.

Answer

Joonisel 14-24 on kujutatud veega täidetud paak. Näidatud on viis horisontaalset „põrandat” ja „lage”; kõik nad on sama pindalaga ja asetsevad veepinnast kaugustel $L$ , $2 L$ või $3 L$ . Järjestage nad neile mõjuvate jõudude järgi, suurimast alustades.

Answer

Sukeldame ebakorrapärase kujuga materjalikamaka massiga $3 kg$ täielikult vedelikku. Vedeliku mass, mis asus nüüd selle keha poolt hõivatud ruumalas, on $2 kg$ . (a) Kui me kamaka lahti laseme, kas ta kerkib ülespoole, vajub allapoole või jääb paigale? (b) Kui me järgnevalt sukeldame sama kamaka väiksema tihedusega vedelikku ja jälle vabaks laseme, mida ta teeb?

Answer

Joonisel 14-25 on kujutatud neli situatsiooni, kus punane vedelik ja hall vedelik asuvad U-torus. Ühes neist ei saa vedelikud olla staatilises tasakaalus. (a) Milline situatsioon see on? (b) Ülejäänud kolmel juhul eeldage staatilist tasakaalu. Igaühe jaoks nendest – kas punase vedeliku tihedus on suurem, väiksem või võrdne halli vedeliku tihedusega?

Answer

Paat ankruga pardal ujub basseinis, mis on paadist mõneti laiem. Kas veetase basseinis tõuseb, langeb või jääb saamaks, kui ankur (a) visatakse vette või (b) visatakse kaldale? (c) Kas veetase basseinis tõuseb, langeb või jääb samaks, kui selle asemel visatakse paadist vette kork, mis ujuma jääb?

Answer

Joonisel 14-26 on kujutatud kolm identset veega triiki täidetud anumat; kahes neist ujub mängupart. Järjestage konteinerid ja nende sisu kaalu järgi, suurimast alustades.

Answer

Vesi voolab laminaarselt horisontaalses torus. Joonisel 14-27 on kujutatud vee-elemendi kineetiline energia liikumisel piki x-telge, mis on suunatud mööda toru. Järjesta kolm tähtedega tähistatud lõiku toru raadiuse järgi, suurimast alustades.

Answer

Joonisel 14-28 on kolme vedeliku jaoks kujutatud manomeetrilise rõhu $p_{man}$ sõltuvus sügavusest $h$ . Järjesta vedelikud üleslükkejõu järgi, mida nad avaldavad neisse täielikult sukeldatud plasthelmele, alustades suurimast.

Answer

Joonisel 14-29 on kujutatud neli erinevalt muutuva läbimõõduga toru, läbi mille vesi voolab laminaarselt paremale. Näidatud on torulõikude raadiused. Millise järjestuse korral on ühikulise veehulga kallal süsteemi läbimisel tehtav kogutöö (a) null, (b) positiivne ja (c) negatiivne?

Answer

Risttahukakujulist klotsi sukeldatakse järjestikku kolme erinevasse vedelikku, üks tahk paralleelselt vedeliku pinnaga. Klotsi näiva kaalu $W_{n ¨ a iv}$ sõltuvus sügavusest $h$ on kujutatud joonisel 14-30. Järjestage vedelikud nende ruumalaühiku kaalu järgi, alustades suurimast.

Answer

Ülesanded

Punkt 14-3 Tihedus ja rõhk Punkt 14-4 Liikumatud voolised Punkt 14-5 Rõhu mõõtmine Punkt 14-6 Pascali seadus Punkt 14-7 Archimedese seadus Punkt 14-9 Pidevuse võrrand Punkt 14-10 Bernoulli võrrand Additional tasks

(a)

(b)

KONTROLLKÜSIMUS 1

Näidisülesanne 14-2

Näidisülesanne 14.3

KONTROLLKÜSIMUS 2

Näidisülesanne 14-4

(a)

(b)

KONTROLLKÜSIMUS 3

Näidisülesanne 14-6

KONTROLLKÜSIMUS 4

Näidisülesanne 14-7

Näidisülesanne 14-8

(a)

(b)

Tihedus

Voolise rõhk

Rõhu muutumine kõrguse ja sügavusega

Pascal's law

Archimedese seadus

Ideaalsete vooliste voolamine

Bernoulli võrrand