Ajal on suund, nimelt see, kuhupoole me vananeme. Oleme harjunud ühesuunaliste protsessidega, mis saavad toimuda ainult kindlas ajalises järjestuses (õiges suunas) ja mitte kunagi vastupidises järjestuses (vales suunas). Muna kukub põrandale, pitsa küpseb, auto sõidab vastu laternaposti, suured lained kulutavad liivaranda – need ühesuunalised protsessid on mittepööratavad, mis tähendab, et nende kulgemise suunda ei saa muuta vastupidiseks väikeste muutustega nende ümbruskonnas.

Füüsika üheks eesmärgiks on aru saada, miks ajal on suund ja miks ühesuunalised protsessid on pöördumatud. Kuigi selline füüsika võib näida igapäevase elu praktilistest küsimustest lahus, asub see tegelikult igasuguse jõumasina südames, näiteks automootoris, sest sellest sõltub, kui hästi mootor töötab.

Võti selle mõistmiseks, miks ühesuunalist protsessi ei saa pöörata, peitub suuruses, mida nimetatakse entroopiaks.

Mittepööratavate protsesside ühesuunaline iseloom on nii valdav, et me võtame neid kui iseenesestmõistetavaid nähtusi. Me oleksime hämmelduses, kui niisugused protsessid kulgeksid spontaanselt (iseeneslikult) vastupidises suunas. Ometi ei rikuks mitte ükski selline protsess energia jäävuse seadust.

Näiteks võttes kätte tassi kuuma kohviga, tekitaks meis hämmeldust, kui käed muutuks külmemaks ja tass soojemaks. See oleks ilmselt vale suund energia ülekandeks, kuigi suletud süsteemi (käed + kohvitass) koguenergia oleks võrdne koguenergiaga protsessi kulgemisel õiges suunas. Teine näide: heeliumiga täidetud õhupalli katki tegemise järel oleks üllatav, kui heeliumi aatomid koguneksid tagasi pallikujulisse ruumi. See oleks ilmselt vale suund molekulide levimiseks, ometi suletud süsteemi (molekulid + ruum) koguenergia oleks sama suur kui õiges suunas levimisel.

Niisiis, energia muutused suletud süsteemi sees ei määra mittepööratavate protsesside suunda. Tegelikult määrab suuna teine omadus, mida selles peatükis käsitletakse – süsteemi entroopia muutus $\Delta S$. Süsteemi entroopia muutus defineeritakse järgmises punktis, kuid siin olgu toodud selle keskne omadus, mida tavaliselt kutsutakse entroopia postulaadiks:

Entroopia erineb energiast selle poolest, et entroopia kohta ei kehti jäävuse seadus. Suletud süsteemi energia on jääv suurus, see jääb alati konstantseks. Mittepööratavas protsessis suletud süsteemi entroopia aga kasvab alati. Selle omaduse tõttu nimetatakse entroopia muutust vahel ka „aja nooleks”. Nii seotakse maisitera lõhkemine popkorni küpsetamisel aja pärisuunaga ja entroopia kasvuga. Aja voolamisele vastassuunas (videolindi tagurpidi kerimisele) vastaks lõhkenud popkornist esialgse maisitera taasmoodustumine. Kuna selline tagurpidine protsess viiks entroopia kahanemisele, ei juhtu seda kunagi.

Süsteemi entroopiat saab defineerida kahel võrdväärsel viisil: (1) süsteemi temperatuuri ja süsteemi soojusenergia kao või kasvu kaudu ja (2) lugedes kokku võimalused süsteemi kuuluvate aatomite või molekulide paigutamiseks. Esimest lähenemist kasutatakse järgmises punktis ja teist punktis 20-8.

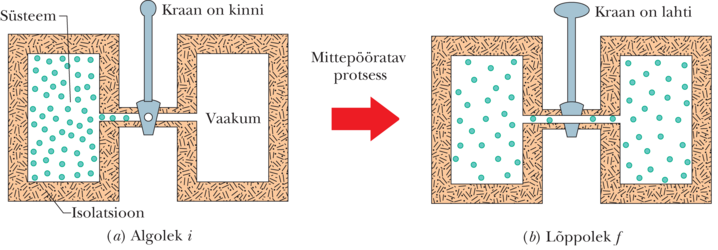
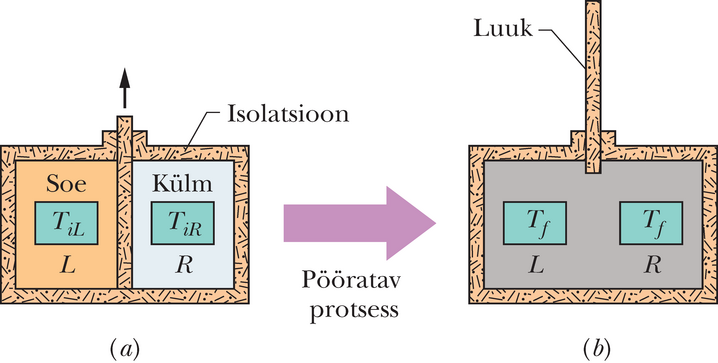
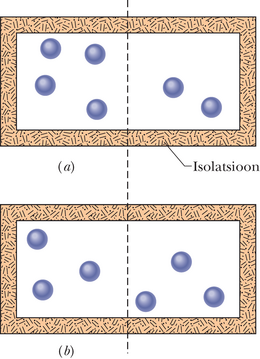
Entroopia muutuse definitsiooni saab kätte, kui vaadelda uuesti punktides 18-11 ja 19-11 kirjeldatud protsessi: ideaalse gaasi vaba paisumist. Joonisel 20-1a on gaasi esialgseks tasakaaluolekuks $i$ olla kraani abil suletud soojuslikult isoleeritud anuma vasakusse poolde. Kraani avamise järel täidab gaas kiiresti kogu anuma, mille tagajärjel saabub joonisel 20-1b kujutatud tasakaaluline lõppolek $f$. Protsess on mittepööratav, mitte kunagi ei kogune kõik molekulid anuma vasakusse poolde tagasi.

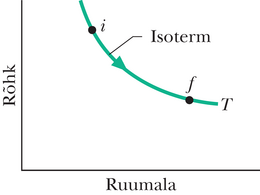
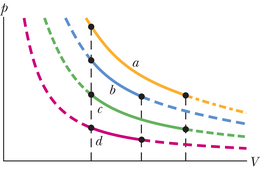
Joonisel 20-2 on gaasi rõhk ja temperatuur algolekus $i$ ja lõppolekus $f$ esitatud koordinaatides $p-V$. Rõhk ja ruumala on olekuparameetrid, iseloomustavad suurused, mis sõltuvad ainult gaasi olekust ja mitte sellest, kuidas see olek saavutati. Teised olekuparameetrid on temperatuur ja energia. Olgu gaasil veel üks olekuparameeter – gaasi entroopia. Defineerime entroopia muutuse $S_f–S_i$ protsessi käigus, mis viib süsteemi algolekust $i$ lõppolekusse $f$ avaldisega

Siin $Q$ on energia, mis kanti protsessis süsteemi sisse või süsteemist välja ja $T$ on süsteemi temperatuur kelvinites. Seega entroopia muutus ei sõltu mitte ainult ülekantud soojusenergiast, vaid ka temperatuurist, mille juures ülekanne sooritati. Kuna $T$ on alati positiivne, siis $\Delta S$ ja $Q$ on sama märgiga. Valemist 20-1 tuleneb, et entroopia ja entroopia muutuse SI ühik on džauli kelvini kohta.

Valemi 20-1 rakendamisel joonisel 20-1 kujutatud vaba paisumise kirjeldamiseks tekib järgmine probleem. Kui gaas täidab kiirelt paisudes anuma, muutuvad gaasi rõhk, ruumala ja temperatuur ettearvamatul viisil. Teiste sõnadega, siirdel tasakaalulisest algolekust $i$ tasakaalulisse lõppolekusse $f$ ei läbi need suurused kindlalt määratud tasakaalulisi vahepealseid väärtusi. Sellepärast ei saa joonisel 20-2 kujutada oleku muutust joonega $p-V$ koordinaatides, ja mis veelgi olulisem, pole võimalik leida seost $Q$ ja $T$ vahel, mis lubaks sooritada valemis 20-1 nõutud integreerimistehet.

Ent kui entroopia on tõesti olekuparameeter, siis entroopiate vahe olekute $i$ ja $f$ vahel peab sõltuma ainult nendest olekutest ja üldse mitte teekonnast ühest olekust teise. Oletame siis, et mittepööratav vaba paisumine joonisel 20-1 asendatakse pööratava protsessiga, mis viib olekust $i$ olekusse $f$. Pööratava protsessi korral on rõhu ja ruumala vahelist sõltuvust $p-V$ koordinaatides võimalik üles joonistada, leida seos $Q$ ja $T$ vahel ning kasutada valemit 20-1 entroopia muutuse arvutamiseks.

Nägime punktis 19-11, et vaba paisumise korral ideaalse gaasi temperatuur ei muutu: $T_i=T_f=T$. Järelikult peavad punktid $i$ ja $f$ joonisel 20-2 asuma samal isotermil. Sobiv asendusprotsess on seega pööratav isotermiline paisumine olekust $i$ olekusse $f$, mis tõepoolest kulgeb piki seda isotermi. Pärast seda lihtsustub integraal avaldises 20-1 märgatavalt, kuna $T$ on kogu pööratava isotermilise paisumise vältel konstantne.

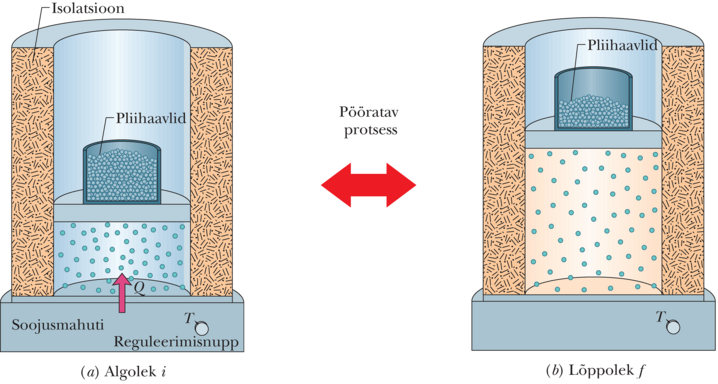
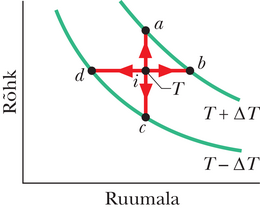
Joonisel 20-3 on näidatud, kuidas sellist pööratavat isotermilist paisumist sooritada. Gaas tuleb sulgeda isoleeritud silindrisse, mis asetseb temperatuuril $T$ hoitaval soojusmahutil. Alustuseks koormame liikuvat kolbi haavlitega just niipalju, et gaasi rõhk ja ruumala oleksid niisugused, nagu algolekus $i$ joonisel 20-1a. Seejärel eemaldame haavleid ükshaaval, kuni gaasi rõhk ja ruumala omandavad joonisel 20-2 kujutatud lõppoleku $f$ väärtused. Gaasi temperatuur ei muutu, sest gaas jääb protsessi jooksul mahutiga soojuslikku kontakti.

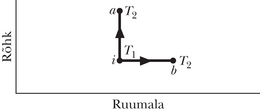
Pööratav isotermiline paisumine joonisel 20-3 erineb füüsikaliselt üsna palju mittepööratavast vabast paisumisest joonisel 20-1. Aga mõlemal protsessil on alg- ja lõppolek sama ja seetõttu peab entroopia muutus olema ühesuurune. Kuna haavleid eemaldati vähehaaval, olid vaheolekud tasakaalulised ja sellepärast saab neid kanda $p-V$ diagrammile (joonis 20-4).

Valemi 20-1 kasutamiseks isotermilise paisumise juhul võtame konstantse temperatuuri $T$ integraali ette, nii et

Kuna $\int dQ=Q$, kus $Q$ on protsessi jooksul ülekantud kogu soojusenergia, siis

Et hoida gaasi temperatuuri $T$ joonisel 20-3 kujutatud isotermilisel paisumisel konstantsena, peab soojushulk $Q$ üle kantama mahutist gaasi. Sellepärast on $Q$ positiivne ja gaasi entroopia kasvab nii isotermilises protsessis kui ka joonisel 20-1 kujutatud vabal paisumisel.

Kokkuvõte:

Kui temperatuuri muutus $\Delta T$ on väike võrreldes protsessi alg- ja lõpptemperatuuridega (kelvinites), siis võib entroopia muutust lähendada valemiga

kus $T_k$ on süsteemi keskmine temperatuur protsessi jooksul.

KONTROLLKÜSIMUS 2

Joonisel toodud p-V diagrammil on ideaalsel gaasil algolekus $i$ temperatuur $T_1$. Lõppolekutes $a$ ja $b$, kuhu viivad näidatud teed, on gaasi temperatuur $T_2$ kõrgem. Kas entroopia muutus siirdel punkti $a$ on suurem, väiksem või võrdne muutusega siirdel punkti $b$?

Näidisülesanne 20-2 Arenda oma oskusi

Joonis 20-5a kujutab kahte identset vaskklotsi massiga $m=1,5kg$: klots $L$ temperatuuriga $T_{iL}=60{}^{\circ }C$ ja klots $R$ temperatuuriga $T_{iR}=20{}^{\circ }C$ asuvad soojusisolatsiooniga kastis ning on eraldatud isoleeriva luugiga. Kui luuk eemaldada, omandavad klotsid tasakaalulise lõpptemperatuuri $T_f=40{}^{\circ }C$ (joonis 20-5b). Kui suur on kahest klotsist koosneva süsteemi koguentroopia muutus selle mittepööratava protsessi jooksul? Vase erisoojus on $386J/kg\cdot K$.

Lahendus

JUHTMÕTE Entroopia muutuse arvutamiseks peame leidma pööratava protsessi, mis viib süsteemi joonisel 20-5a kujutatud algolekust joonisel 20-5b kujutatud lõppolekusse. Valemi 20-1 abil saame arvutada koguentroopia muutuse $\Delta S_{\text{p}\ddot{\text{o}}\ddot{\text{o}}\text{ratav}}$ pööratava protsessi jaoks; seesama $\Delta S_{\text{p}\ddot{\text{o}}\ddot{\text{o}}\text{ratav}}$ on ka mittepööratava protsessi entroopia muutus.

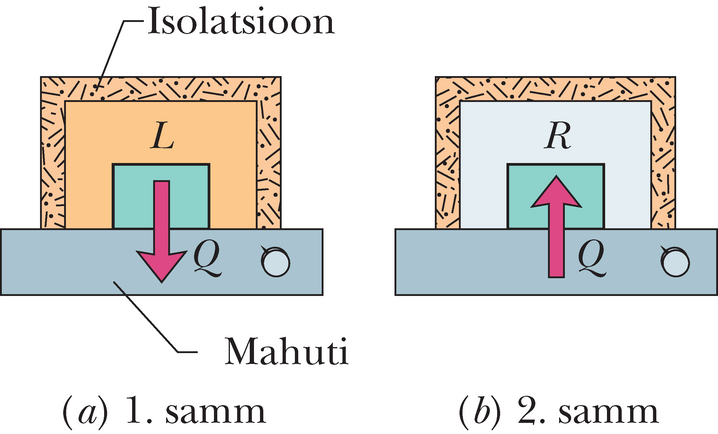
​​​​​​​Arvutused: Pööratava protsessi sooritamiseks vajame soojusmahutit, mille temperatuuri saab muuta aeglaselt (näiteks nuppu keerates). Sooritame klotsidega kaks alljärgnevat, joonisel 20-6 kujutatud protseduuri.

1. samm Fikseerinud mahuti temperatuuri $60{}^{\circ }C$, paigutame sinna klotsi $L$. (Kuna klotsi ja mahuti temperatuur on sama, siis on nad juba soojuslikus tasakaalus.) Seejärel langetame aeglaselt mahuti ja klotsi temperatuuri $40{}^{\circ }C$‑ni. Kui klotsi temperatuur muutub igal sammukesel $dT$ võrra, siis energia $dQ$ siirdub soojusena klotsist mahutisse. Valemit 18-14 abiks võttes saame ülekantud energia jaoks avaldise $dQ=mcdT$, kus $c$ on vase erisoojus. Seose 20-1 kohaselt on klotsi $L$ entroopia muutus $\Delta S_L$ temperatuuri muutudes algväärtusest $T_{iL}$ ($=60{}^{\circ }C=333K$) lõpptemperatuurini $T_f$ ($=40{}^{\circ }C=313K$)

$\Delta S_L={\int }_i^f\frac{dQ}{T}={\int }_{T_{iL}}^{T_f}\frac{mcdT}{T}=mc{\int }_{T_{iL}}^{T_f}\frac{dT}{T}=mc\ln \frac{T_f}{T_{iL}}$

Kasutades eeltoodud väärtusi, saame

$\Delta S_L=(1,5kg)\left(386J/kg\cdot K\right)\ln \frac{313K}{333K}=+35,86J/K$

2. samm Fikseerinud mahuti temperatuuri $20{}^{\circ }C$, paigutame sinna klotsi $R$. Tõstame aeglaselt mahuti ja klotsi temperatuuri kuni $40{}^{\circ }C$. Muutuse $\Delta S_L$ leidmisega analoogset mõttekäiku kasutades saame näidata, et klotsi $R$ entroopia muutus $\Delta S_R$ vaadeldud protsessi käigus on

$\Delta S_R=(1,5kg)\left(386J/kg\cdot K\right)\ln \frac{313K}{293K}=+38,23J/K$

Kahesammulise pööratava siirde sooritanud kahe klotsi süsteemi entroopia kogumuutus on seega

$\Delta S_{\text{p}\ddot{\text{o}}\ddot{\text{o}}\text{ratav}}=\Delta S_L+\Delta S_R=–35,86J/K+38,23J/K=2,4J/K$

Nii on summaarne entroopia muutus DSmittepööratav kahe klotsi tegelikult mittepöörataval siirdel

$\Delta S_{\text{mittep}\ddot{\text{o}}\ddot{\text{o}}\text{ratav}}=\Delta S_{\text{p}\ddot{\text{o}}\ddot{\text{o}}\text{ratav}}=\underset{–}{\underset{–}{2,4J/K}}$

Tulemuseks on positiivne arvväärtus vastavuses punktis 20-2 esitatud entroopia postulaadile.

Järgnevalt midagi peamurdmiseks. Näidisülesandes 20-1 nägime, et kui sooritada joonisel 20-3 kujutatud pööratav protsess olekust (a) olekusse (b), siis gaasi (mille me võtame oma süsteemiks) entroopia muutus on positiivne. Kuid kuna protsess on pööratav, siis võiks sama hõlpsalt siirduda olekust (b) olekusse (a) lihtsalt vähehaaval haavleid joonisel 20-3b kujutatud kolvile asetades, kuni gaasi esialgne ruumala on taastunud. Sellises pööratud protsessis tuleb soojusenergia gaasist välja viia, et vältida temperatuuri tõusu. Järelikult on $Q$ negatiivne ja avaldise 20-2 kohaselt peab gaasi entroopia kahanema.

Kas gaasi entroopia kahanemine ei riku punktis 20-2 esitatud entroopia postulaati, mis väidab, et entroopia kasvab alati? See pole nii, sest postulaat kehtib ainult mittepööratavate protsesside kohta suletud süsteemides. Siin pakutud protsess ei vasta neile nõuetele. Protsess ei ole mittepööratav ja kuna soojusenergia kantakse gaasist mahutisse, siis süsteem – siin ainult gaas – ei ole suletud.

Ent võttes koos gaasiga tervikuks kokku ka mahuti kui süsteemi osa, saame suletud süsteemi. Kontrollime suurendatud süsteemi – gaas + mahuti – entroopia muutust protsessis olekust (b) olekusse (a) joonisel 20-3. Selles pööratavas protsessis kantakse soojusenergia gaasist mahutisse, see tähendab, suurendatud süsteemi ühest osast teise. Olgu $\left|Q\right|$ selle soojushulga absoluutväärtus (suurus). Valemi 20-2 abil võime eraldi arvutada entroopia muutuse gaasis (mis annab $\left|Q\right|$ ära) ja mahutis (mis saab $\left|Q\right|$ juurde). Tulemus on

ja

Suletud süsteemi entroopia muutus on nende kahe suuruse summa: null.

Selle tulemuse abil saab punktis 20-2 toodud entroopia postulaati modifitseerida, et see hõlmaks nii pööratavaid kui mittepööratavaid protsesse.

Suletud süsteemi entroopia võib küll mõnes süsteemi osas kahaneda, kuid siis toimub mõnes teises süsteemi osas sama suur või suurem entroopia kasv, nii et süsteemi kui terviku entroopia ei kahane kunagi. See asjaolu on üks võimalik termodünaamika teise seaduse formulatsioon, mida kirjutatakse kujul

kus võrratusemärk kehtib mittepööratava ja võrdusmärk pööratava protsessi korral. Avaldis 20-5 kehtib ainult suletud süsteemides.

Tegelikus maailmas on peaaegu kõik protsessid mõningal määral mittepööratavad hõõrdumise, turbulentsi ja teiste tegurite tõttu, seepärast reaalsetes suletud süsteemides, kus toimuvad reaalsed protsessid, entroopia alati kasvab. Sellised protsessid, milles entroopia jääb konstantseks, on alati vaid idealisatsioonid.

Entroopiast põhjustatud jõud

Et aru saada, miks kumm osutab venitamisele vastupanu, lähtume termodünaamika esimesest seadusest

$dE=dQ-dW$

kummipaela jaoks, mida käte vahel venitatakse ja mille pikkus saab väikese juurdekasvu $dx$. Paela poolt tekitatav jõud olgu $F$, see on suunatud paela sisse ja sooritab pikenemise $dx$ jooksul töö $dW=–Fdx$. Valemit 20-2 ($\Delta S=Q/T$) rakendades saame, et väikesed $Q$ ja $S$ muutused konstantsel temperatuuril avalduvad kujul $dS=dQ/T$ ehk $dQ=TdS$. Esimese seaduse saab nüüd üles kirjutada nii:

(20-6)

$dE=TdS-Fdx$

Kummipaela siseenergia muutus $dE$ võrdub heas lähenduses nulliga, kui venitus pole liiga suur. Tehes sellise asenduse valemis 20-6, saamegi kummipaela poolt arendatava jõu avaldise:

(20-7)

$F=-T\frac{dS}{dx}$

See valem ütleb, et $F$ on võrdeline entroopia muutumise kiirusega $dS/dx$ kummipaela väikese pikenemise $dx$ ajal. Seega saab kummipaela venitades tajuda entroopia mõju kummi venitavatesse kätesse.

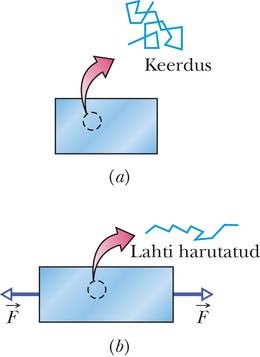
Jõu ja entroopia vahekorra mõistmiseks vaatleme kummitaolise materjali lihtsat mudelit. Kumm koosneb põiksidemetega seotud polümeerahelatest (pikkadest põigiti seotud molekulidest), meenutades kolmedimensionaalseid sik-sakke (joonis 20-7). Rahuolekus kummi polümeerid on spagetitaoliselt keerdus. Molekulide suure korratuse tõttu on entroopia rahuolukorras suur. Kummi venitamisel harutatakse hulk polümeere lahti ja nad reastuvad venituse suunas. Reastumine vähendab korratust, sellepärast on venitatud kummi entroopia väiksem. See tähendab, et muutus $dS/dx$ avaldises (20-7) on negatiivne suurus, kuna entroopia on vähenenud. Niisiis kummipaela poolt kätele mõjuv jõud on tingitud polümeeride püüdest tagasi endisesse korrastamata olekusse ja entroopia suurema väärtuse poole.

Soojusjõumasin ehk lihtsamalt jõumasin on seade, mis ammutab energiat oma ümbruskonnast soojuse kujul ja sooritab kasulikku tööd. Iga jõumasina südames asub töötav aine. Aurumasinas on selleks vesi nii auru kui vedeliku kujul. Automootoris on töötavaks aineks bensiini ja õhu segu. Kui tahetakse, et jõumasin teeks tööd jätkusuutlikult, siis peab aine töötama tsükliliselt; see tähendab, et aine läbib seeria termodünaamilisi protsesse, mida nimetatakse käikudeks, pöördudes uuesti ja uuesti tagasi oma tsükli igasse olekusse. Järgnevas vaatame, mida ütleb termodünaamika jõumasinate töötamise kohta.

Carnot’ jõumasin

Nägime, et reaalsete gaaside kohta võib palju teada saada, analüüsides ideaalseid gaase, mis alluvad lihtsale seadusele $pV=nRT$. Kuigi ideaalset gaasi pole olemas, läheneb ideaalsele käitumisele iga reaalne gaas, kui selle tihedus on küllalt väike. Samamoodi saab uurida reaalsete jõumasinate omadusi, analüüsides ideaalse jõumasina käitumist.

Ideaalses jõumasinas kulgevad kõik protsessid pööratavalt ja puuduvad igasugused kasutud energia lekked, näiteks hõõrdumise või turbulentsi tõttu.

Keskendume erilisele ideaalsele jõumasinale, mida nimetatakse Carnot’ jõumasinaks prantsuse teadlase ja inseneri N. L. Sadi Carnot’ [karnoo] järgi, kes esitas selle idee aastal 1824. See jõumasin osutus parimaks vahendiks (põhimõtteliselt) soojusenergia muutmisel kasulikuks tööks. Üllataval kombel suutis Carnot selle jõumasina talitust analüüsida enne termodünaamika esimese seaduse ja entroopia mõiste avastamist.

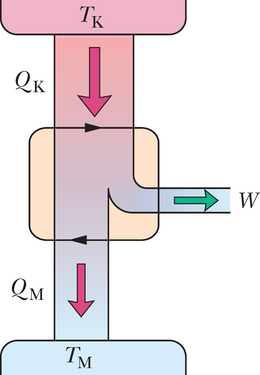
Joonisel 20-8 on skematiseeritud Carnot’ jõumasina tegevus. Igas tsüklis neelab töötav substants energia $\left|Q_K\right|$ soojusena mahutist konstantsel temperatuuril $T_K$ ja väljutab energia $\left|Q_M\right|$ soojusena teise mahutisse, mis on madalamal konstantsel temperatuuril $T_M$.

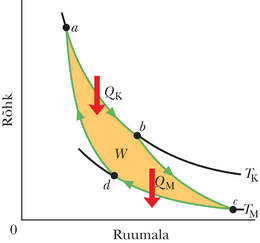
Joonisel 20-9 on $pV$-koordinaatides kujutatud Carnot’ tsükkel, mille töötav aine läbib. Nooled näitavad, et tsükkel läbitakse kellaosuti liikumise suunas. Olgu töötavaks aineks isoleerivasse silindrisse suletud gaas, mis on koormatud liikuva kolviga. Silindri võib asetada suvaliselt kas ühele kahest soojusmahutist nagu joonisel 20-6 või isoleerivale alusele. Joonisel 20-9 on näidatud, et kui asetada silinder kokkupuutesse kõrgemal temperatuuril mahutiga temperatuuril $T_K$, siis siirdub soojushulk $\left|Q_K\right|$ mahutist töötavale ainele, kuna viimane paisub isotermiliselt ruumalast $V_a$ ruumalani $V_b$. Sarnaselt, kui töötav aine on kokkupuutes madalama temperatuuriga mahutiga temperatuuril $T_M$, siirdub soojushulk $\left|Q_M\right|$ töötavast ainest madalama temperatuuriga mahutisse, kuna gaas surutakse isotermiliselt kokku ruumalast $V_c$ ruumalani $V_d$.

Joonisel 20-8 kujutatud jõumasina kohta eeldame, et töötav aine saab soojust juurde või annab soojust ära ainult isotermiliste protsesside $ab$ ja $cd$ vältel, mida kujutab joonis 20-9. Seetõttu protsessid $bc$ ja $da$, mis ühendavad sellel joonisel kahte isotermi temperatuuridega $T_K$ ja $T_M$, peavad olema (pööratavad) adiabaatilised protsessid; see tähendab, et nad peavad olema niisugused, mille kestel soojusenergiat üle ei kandu. Et seda garanteerida, asetatakse silinder isoleerivale alusele protsesside $bc$ ja $da$ ajaks, mil töötava aine ruumala muutub.

Järjestikuste protsesside $ab$ ja $bc$ ajal (joonisel 20-9) töötav aine paisub ja sooritab positiivse töö, sest see kergitab koormatud kolbi. Tööd esitab joonisel 20-9 kõvera $abc$ alune pindala. Järjestikuste protsesside $cd$ ja $da$ kestel surutakse töötav aine kokku, mis tähendab, et see sooritab ümbritseva keskkonna kallal negatiivse töö, mis on samaväärne keskkonna poolt sooritatud tööga aine kallal, kui koormatud kolb vajub alla. Seda tööd esitab pindala kõvera $cda$ all. Töötsükli vältel sooritatud netotöö (kasulik töö), mida joonistel 20-8 ja 20-9 tähistab $W$, on nende kahe pindala vahe, see on positiivne ja võrdub pindalaga kinnise kõvera $abcda$ sees joonisel 20-9. See töö $W$ sooritatakse mingi välise objekti kallal, milleks on näiteks tõstetav koorem.

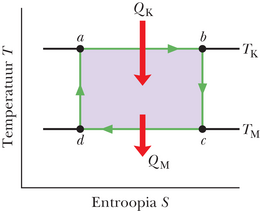
Avaldis 20-1 ($\Delta S=\int dQ/T$) väidab, et iga energiaülekandega peab entroopia muutuma. Carnot’ jõumasinaga seotud entroopia muutu kujutab joonis 20-10, millel Carnot’ tsükkel on esitatud temperatuuri ja entroopia ($T-S$) koordinaatides. Tähistatud punktid $a$, $b$, $c$, ja $d$ joonisel 20-10 vastavad tähistatud punktidele $p-V$ koordinaatides joonisel 20-9 kujutatud diagrammil. Kaks horisontaalset joont joonisel 20-10 vastavad Carnot’ tsükli kahele isotermilisele protsessile (sest temperatuur on konstantne). Protsess $ab$ on tsükli isotermiline paisumine. Kuna töötav aine neelab (pööratavalt) energia $\left|Q_K\right|$ soojusena konstantsel temperatuuril $T_K$ paisudes, siis selle entroopia kasvab. Samuti, isotermilise kokkusurumise $cd$ ajal kaotab töötav substants (pööratavalt) energia $\left|Q_M\right|$ soojusena konstantsel temperatuuril $T_M$ ja entroopia kahaneb.

Kaks vertikaalset joont joonisel 20-10 vastavad Carnot’ tsükli kahele adiabaatilisele protsessile. Kuna soojusenergiat nende kahe protsessi kestel üle ei kanta, on töötava aine entroopia sel ajal konstantne.

Töö. Carnot’ jõumasina tsükli jooksul sooritatud netotöö arvutamiseks rakendame töötavale ainele valemit 18-26, termodünaamika esimest seadust ($\Delta E_{sise}=Q–W$). Aine peab ikka ja jälle tagasi tulema meelevaldselt valitud olekusse tsüklis. Seega, kui $X$ tähistab aine mingit olekut iseloomustavat suurust nagu rõhk, temperatuur, ruumala, siseenergia või entroopia, siis peab iga tsükli järel kehtima $\Delta X=0$. Järelikult $\Delta E_{sise}=0$ töötava aine täistsükli lõpuks. Meenutades, et $Q$ avaldises 18-26 on soojuse netoülekanne tsüklis ja $W$ on netotöö, saame termodünaamika esimesele seadusele Carnot’ tsükli korral anda kuju

(20-8)

$W=\left|Q_K\right|-\left|Q_M\right|$

Entroopia muutused. Carnot’ jõumasinas on kaks (ja ainult kaks) pööratavat soojusenergia ülekannet ja seega kaks töötava aine entroopia muutumist – üks temperatuuril $T_K$ ja teine temperatuuril $T_M$. Entroopia netomuutus tsüklis on

(20-9)

$\Delta S=\Delta S_K+\Delta S_M=\frac{\left|Q_K\right|}{T_K}-\frac{\left|Q_M\right|}{T_M}$

Siin on $\Delta S_K$ positiivne, sest soojusenergia $\left|Q_K\right|$ liidetakse töötavale ainele (entroopia kasvab) ja $\Delta S_M$ on negatiivne, sest soojusenergia $\left|Q_M\right|$ eemaldatakse töötavast ainest (entroopia kahaneb). Kuna entroopia on olekufunktsioon, peab kogu tsükli jaoks kehtima $\Delta S=0$. Seda arvestades teiseneb (20-9) nõudeks

(20-10)

$\frac{\left|Q_K\right|}{T_K}=\frac{\left|Q_M\right|}{T_M}$

Tuleb tähele panna, et kuna $T_K>T_M$, siis ka $\left|Q_K\right|>\left|Q_M\right|$, seega ammutatakse soojemast mahutist rohkem energiat kui antakse ära külmemasse mahutisse.

Järgmiseks tuletame avaldiste 20-8 ja 20-10 abil valemi Carnot’ jõumasina efektiivsuse arvutamiseks.

Carnot’ jõumasina kasutegur

Igasuguse jõumasina eesmärk on võimalikult palju ammutatud energiast $Q_K$ tööks muuta. Masina edukust selles tegevuses mõõdetakse soojusliku kasuteguriga $ϵ$, mida defineeritakse kui tööd, mida jõumasin tsüklis teeb („energiasaak”), mis on jagatud energiaga, mille masin tsüklis neelab („energiakulu”):

(igasuguse jõumasina kasutegur, 20-11)

$ϵ=\frac{\text{energia, mille me j}\tilde{\text{o}}\text{umasinalt saame}}{\text{energia, mille eest me maksame}}=\frac{\left|W\right|}{\left|Q_K\right|}$

Carnot’ jõumasina korral, asendades avaldises 20-11 $W$ avaldisest 20-8 saame

(20-12)

${ϵ}_C=\frac{\left|Q_K\right|-\left|Q_M\right|}{Q_K}=1-\frac{\left|Q_M\right|}{\left|Q_K\right|}$

Avaldise 20-10 abil võib sellele anda kuju

(Carnot' jõumasina kasutegur, 20-13)

${ϵ}_C=1-\frac{T_M}{T_K}$

kus temperatuurid $T_K$ ja $T_M$ on kelvinites. Kuna $T_M<T_K$, siis on Carnot’ jõumasina soojuslik kasutegur väiksem kui üks, s.t alla $100$. Seda illustreerib joonis 20-8, mis näitab, et vaid osa soojemast mahutist ammutatud soojusenergiast on kasutatav töö tegemiseks ja ülejäänud osa antakse külmemasse mahutisse. Punktis 20-7 saame näha, et mitte ühegi reaalse jõumasina soojuslik kasutegur ei saa olla suurem kui valemi 20-13 abil arvutatav.

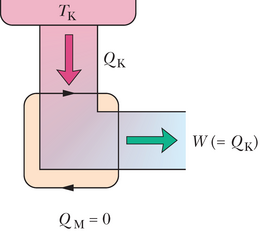
Leidurid püüavad pidevalt suurendada jõumasinate efektiivsust, vähendades energiat $\left|Q_M\right|$, mis igas tsüklis raisku läheb. Leiduri unistus on valmistada joonisel 20-11 skitseeritud täiuslik jõumasin, milles $\left|Q_M\right|$ on kahandatud nullini ja $\left|Q_K\right|$ muundatakse tervenisti tööks. Selline jõumasin ookeanilaeval võiks ammutada soojusenergiat veest ja panna sellega tööle propellerid, hoides nii kütusekulud täielikult kokku. Sellise mootoriga auto võiks ammutada välisõhust soojusenergiat ja kasutada seda liikumiseks, jällegi säästes kütusekulusid. Kahjuks on täiuslik jõumasin vaid unistus: valemit 20-13 vaadates näeme kohe, et $100$ jõumasina efektiivsuse ($ϵ=1$) saame vaid siis, kui kas $T_M=0$ või $T_K\to \infty$, mis on võimatud nõuded. Selle asemel pakub kogemus välja termodünaamika teise seaduse alternatiivse versiooni, mis lühidalt ütleb, et täiuslikku jõumasinat ei ole olemas.

Pole võimalik sooritada protsesside järjestust, mille ainsaks tulemuseks on mahutist ammutatud soojusenergia jäägitu muundamine tööks.

Kokkuvõtteks: valemiga 20-13 esitatud soojuslik kasutegur kehtib vaid Carnot’ jõumasinate korral. Reaalsetes jõumasinates, mille töötsükli moodustavad protsessid ei ole pööratavad, on kasutegur madalam. Kui auto mootoriks oleks Carnot’ jõumasin, siis selle kasutegur oleks valemi 20-13 põhjal $55$; tegelik väärtus on tõenäoselt $25$. Tuumajaam (joonis 20-12) on tervikuna võttes jõumasin. See võtab soojusenergiat reaktori südamikust, sooritab turbiini abil töö ja eritab soojusenergiat lähimasse jõkke. Kui jõujaam kasutaks Carnot’ tsüklit, oleks selle kasutegur umbes $40$, tegelik väärtus on ligikaudu $30$. Igat liiki jõumasinate projekteerimisel lihtsalt pole mingit võimalust ületada valemiga 20-13 antud piiri.

Stirlingi jõumasin

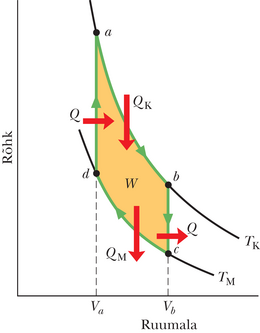
Valem 20-13 ei kehti kõigi ideaalsete jõumasinate korral, vaid ainult nende jaoks, mida esitab joonis 20-9, nimelt Carnot’ jõumasinate jaoks. Näiteks joonisel 20-13 on kujutatud ideaalse Stirlingi jõumasina töötsükkel. Võrdlus Carnot’ tsükliga jooniselt 20-9 näitab, et mõlemas toimub isotermiline soojuse ülekanne temperatuuridel $T_K$ ja $T_M$. Kuid Stirlingi tsüklis pole kaks isotermi ühendatud mitte adiabaatiliste protsessidega nagu Carnot’ tsüklis, vaid protsessidega, milles ruumala ei muutu. Gaasi temperatuuri tõstmine konstantses ruumalas väärtuselt $T_M$ väärtuseni $T_K$ pööratavalt (protsess $da$ joonisel 20-13) nõuab soojusenergia ülekannet töötavale aine mahutist, mille temperatuur muutub sujuvalt nende piirväärtuste vahel. Samasugust ülekannet vastassuunas nõuab protsess $bc$. Seepärast toimuvad pööratavad soojuse ülekanded (ja vastavad entroopia muutused) kõigis neljas protsessis, mis moodustavad Stirlingi tsükli, mitte vaid kahes, nagu Carnot’ jõumasinas. Samal põhjusel ei kõlba valemi 20-13 tuletuskäik ideaalse Stirlingi jõumasina kirjeldamiseks. Veelgi olulisem on asjaolu, et ideaalse Stirlingi jõumasina efektiivsus on väiksem kui samade temperatuuride vahel töötaval Carnot’ jõumasinal. Reaalse Stirlingi jõumasina efektiivsus on muidugi veel väiksem.

Stirlingi jõumasina töötas välja Robert Stirling 1816. aastal. See masin, mida pikka aega ignoreeriti, leiab nüüd arendust autode ja kosmoseaparaatide tarvis. On valmistatud Stirlingi jõumasin võimsusega $5000hj$ ($3,7MW$). Kuna Stirlingi jõumasinad töötavad vaikselt, kasutatakse neid mõnedes sõjaväe allveelaevades.

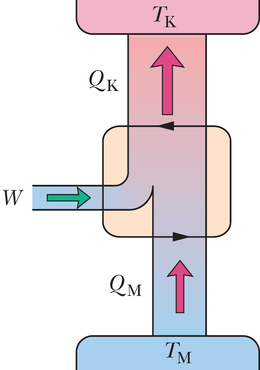
Külmuti (külmamasin) on seade, mis kasutab tööd, et kanda energiat madala temperatuuriga mahutist kõrge temperatuuriga mahutisse, sooritades korduvate termodünaamiliste protsesside sarja. Näiteks koduses külmutuskapis sooritab tööd elektrikompressor, kandes energiat toiduainete säilitamiseks mõeldud kapist (madala temperatuuriga mahutist) kööki (kõrge temperatuuriga mahutisse).

Õhukonditsioneerid ja soojuspumbad on samuti külmamasinad. Erinevus on vaid kõrge ja madala temperatuuriga mahutis. Õhukonditsioneeri korral on madala temperatuuriga mahutiks jahutatav ruum ja kõrge temperatuuriga mahutiks (eelduse kohaselt soojem) välisõhk. Soojuspump on õhukonditsioneer, mis on pandud toa kütmiseks tagurpidi käima, tuba on kõrge temperatuuriga mahuti ja soojust kantakse sisse (eelduse kohaselt külmemast) välisõhust.

Vaatleme ideaalset külmamasinat.

Ideaalse külmamasina peamised elemendid on kujutatud joonisel 20-14. Märkigem, et selle toimimine on vastupidine joonisel 20-8 kujutatud Carnot’ jõumasina omale. Teiste sõnadega, kõik energia ülekanded, kas soojuse või töö kujul, on vastupidised võrrelduna Carnot’ jõumasinaga. Sellist ideaalset külmutit võib nimetada Carnot’ külmamasinaks.

Külmuti projekteerijale meeldiks võtta võimalikult palju energiat $\left|Q_M\right|$ külmast mahutist (seda tahame) vähima tööhulgaga $\left|W\right|$ (seda peame kulutama). Külmuti efektiivsuse mõõduks on seega

kus $K$ kannab nimetust jahutustegur. Carnot’ külmuti korral annab termodünaamika esimene seadus $\left|W\right|=\left|Q_K\right|–\left|Q_M\right|$, kus $\left|Q_K\right|$ on kõrgema temperatuuriga mahutisse viidud soojusenergia väärtus. Selle asendusega saab 20-14 kuju

Kuna Carnot’ külmamasin on tagurpidi töötav Carnot’ jõumasin, siis võime seoseid 20-10 ja 20-15 kombineerides pärast mõningaid teisendusi leida, et

Tüüpilise õhukonditsioneeri korral on $K=2,5$. Kodusel külmikul on $K\approx 5$. Harjumatul kombel on $K$ seda suurem, mida vähem erinevad kahe mahuti temperatuurid. Sellepärast on soojuspumbad mõõduka kliimaga piirkondades efektiivsemad kui seal, kus välistemperatuur on palju madalam kui soovitav sisetemperatuur.

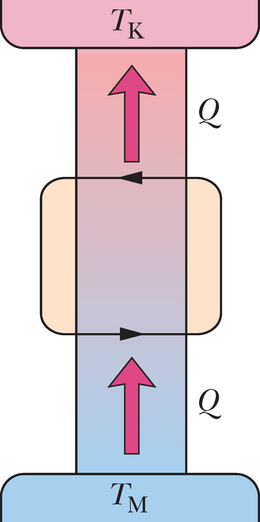
Oleks tore omada külmutit, mis ei nõuaks üldse töö sisestamist, nii et näiteks külmik toimiks pistikut seina pistmata. Joonis 20-15 kujutab teistsugust „leiduri unenägu”, perfektset külmutit, mis viib soojusenergia $Q$ külmast mahutist sooja mahutisse tööd tarvitamata. Kuna seade sooritab tsükleid, siis töötava aine entroopia ei ole täistsükli järel muutunud. Kuid kahe mahuti entroopia on muutunud: külma mahuti entroopia muutus on $–\left|Q\right|/T_M$ ja soojal mahutil $+\left|Q\right|/T_K$. Summaarne entroopia muutus kogu süsteemil on

Kuna $T_K>T_M$, siis on võrduse parem pool negatiivne ja suletud süsteemi külmuti + mahutid entroopia muutus tsüklis on samuti negatiivne. Selline entroopia kahanemine rikub termodünaamika teist seadust (valem 20-5), seepärast täiuslikku külmamasinat ei ole olemas (kui tahate oma külmiku tööle panna, peate pistiku seina torkama).

See tulemus viib veel ühe (samaväärse) termodünaamika teise seaduse formuleeringuni:

Lühidalt öeldes, täiuslikku külmutit pole olemas.

Olgu ${ϵ}_C$ kahe etteantud temperatuuri vahel töötava Carnot’ jõumasina kasutegur. Tõestame, et mitte ühegi samade temperatuuride vahel töötava reaalse jõumasina kasutegur ei saa olla suurem kui ${ϵ}_C$. Kui see nii ei oleks, rikuks selline jõumasin termodünaamika teist seadust.

Eeldame, et oma garaažis töötav leidur on konstrueerinud masina $X$, mille kasuteguri ${ϵ}_X$ ta väidab olevat suurema kui ${ϵ}_C$:

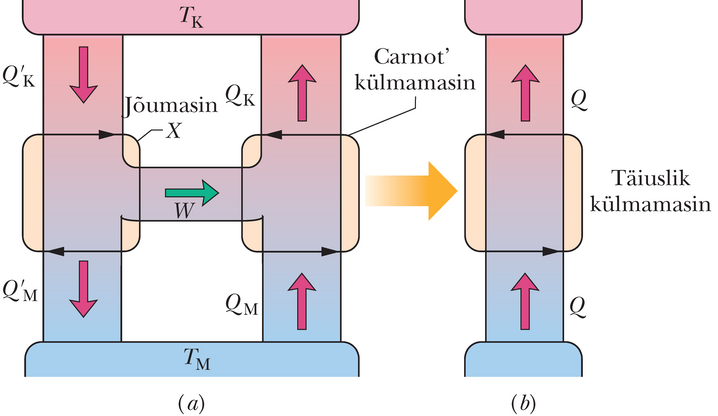
Ühendame jõumasina $X$ Carnot’ külmamasinaga, nagu on kujutatud joonisel 20-16a. Seame Carnot’ külmuti käigu selliseks, et töö, mida see ühes tsüklis vajab, võrdub parajasti jõumasinast $X$ saadava tööga. Siis kombinatsioon jõumasin + külmamasin joonisel 20-16, mille me loeme oma süsteemiks, ei tee tööd väljapoole ega sooritata tööd ka süsteemi kallal.

Kui võrratus 20-17 kehtib, siis kasuteguri definitsioonist (20-11) järeldub

kus primmiga on tähistatud jõumasinat $X$ iseloomustavad suurused ja võrratuse parem pool on Carnot’ külmamasina kasutegur jõumasinana töötades. Võrratusest järgneb

Kuna jõumasina $X$ sooritatud töö võrdub Carnot’ külmamasina sooritatud tööga, tuleneb termodünaamika esimesest seadusest (20-8), et

mille saab kirjutada kujul

Võrratusest 20-18 järeldub, et suurus $Q$ peab olema positiivne.

Seose 20-19 võrdlemine joonisel 20-16 kujutatuga näitab, et jõumasina $X$ ja Carnot’ külmamasina kombinatsiooni summaarne efekt on soojusenergia $Q$ ülekanne madalama temperatuuriga mahutist kõrgema temperatuuriga mahutisse ilma tööd kulutamata. Seega kombinatsioon töötab nagu joonisel 20-15 kujutatud perfektne külmuti, mida termodünaamika teine seadus ei luba.

Miski meie eeldustes peab olema vigane ja see saab olla ainult võrratus 20-17. Järeldame, et mitte ükski reaalne jõumasin ei saa olla suurema kasuteguriga kui Carnot’ jõumasin, kui need töötavad samade temperatuuride vahel. Parimal juhul võib reaalse jõumasina kasutegur olla Carnot’ jõumasina omaga võrdne. Aga siis reaalne jõumasin ongi Carnot’ jõumasin.

Me nägime 19. peatükis, et gaaside makroskoopilisi omadusi saab seletada nende mikroskoopilise ehk molekulaarse käitumise terminites. Meenutame ühe näitena, et gaasi rõhku anuma seintele saime väljendada gaasi molekulide poolt põrkumisel seintele üle kantud impulsi kaudu. Sellised seletused moodustavad osa statistilisest mehaanikast.

Edasises koondame oma tähelepanu ülesandele, mille jaoks on tarvis teada gaasi molekulide jagunemist isoleeritud konteineri kahe poole vahel. See on analüüsiks küllalt lihtne ja võimaldab entroopia muutust ideaalse gaasi vabal paisumisel arvutada statistilise mehaanika abil. Näidisülesanne 20-7 annab statistilist mehaanikat kasutades entroopia muutuse jaoks sama tulemuse, mis tuli näidisülesandes 20-1 välja termodünaamika abil.

Joonisel 20-17 on kujutatud konteiner, mis sisaldab kuut identset (ja seetõttu eristamatut) gaasimolekuli. Igal hetkel on mingi valitud molekul kas konteineri vasakus või paremas pooles; kuna poolte ruumalad on võrdsed, siis molekul asub kummaski pooles ühesuguse tõenäosusega.

Tabelis 20-1 on toodud kuue molekuli seitse võimalikku konfiguratsiooni, mis on tähistatud rooma numbritega. Näiteks on konfiguratsioonis $I$ kõik kuus molekuli konteineri vasakus pooles ($n_1=6$) ja paremas pole ühtki ($n_2=0$). Üldjuhul võib mingit neist konfiguratsioonidest saavutada mitmel viisil. Nimetame neid molekulide erinevaid asetusi mikroolekuteks. Vaatame, kuidas arvutada teatavale konfiguratsioonile vastavate mikroolekute arvu.

Olgu meil $N$ molekuli jagunenud nii, et $n_1$ molekuli on ühes ja $n_2$ molekuli teises pooles. (Seega $n_1+n_2=N$.) Kujutleme, et me jaotame molekule ühekaupa „käsitsi”. Kui $N=6$, siis saame valida esimest molekuli kuuel viisil, sest võime esimesena võtta ükskõik millise kuuest molekulist. Teise molekuli saame valida viiel viisil, võttes ühe molekuli järelejäänud viiest ja nii edasi. Võimaluste koguarv kõigi kuue molekuli valikuks on $6\times 5\times 4\times 3\times 2\times 1=720$. Matemaatiline lühike kirjaviis selle korrutise jaoks on $6!=720$, kus $6!$ loetakse „kuue faktoriaal„. Arvatavasti saate faktoriaale leida oma taskuarvuti abil. Edasiseks peab teadma, et $0!=1$. (Kontrollige seda oma kalkulaatoriga.)

Kuid molekulid on eristamatud ja seepärast pole need $720$ asetust kõik omavahel erinevad. Näiteks juhul $n_1=4$ ja $n_2=2$ (konfiguratsioon $III$ tabelis 20-1) pole oluline nelja molekuli konteineri ühte poolde paigutamise järjekord, sest pärast seda, kui kõik neli molekuli on paigutatud, pole mingit võimalust öelda, mis järjekorras seda tehti. See nelja molekuli paigutamise võimalike järjekordade arv on $4!=24$. Võimalik järjekordade arv kahe molekuli paigutamiseks konteineri teise poolde on $2!=2$. Et saada erinevate paigutuste arvu, mis annaks ($4$; $2$) jaotuse konfiguratsioonis $III$, tuleb $720$ jagada $24$-ga ja veel $2$-ga. Saadud suurus, teatavale konfiguratsioonile vastavate mikroolekute arv, kannab nimetust „teatud konfiguratsiooni kordsus $W$”. Järelikult konfiguratsiooni $III$ kordsus on

Seepärast annab tabel 20-1, et konfiguratsioonile $III$ vastab 15 sõltumatut mikroolekut. Paneme ka tähele, et tabel annab seitsme konfiguratsiooni vahel jagunevate kuue molekuli mikroolekute koguarvuks 64.

Üldistus kuuelt molekulilt $N$ molekulile annab üldjuhul

Proovige järele, kas valem 20-20 annab kõigi tabelis 20-1 loetletud konfiguratsioonide kordsuse.

Statistilise mehaanika põhieelduseks on väide

Teiste sõnadega, kui teeme joonisel 20-17 kujutatud konteineris rüselevast kuuest molekulist suure hulga momentvõtteid ja seejärel loeme kokku, mitu korda iga mikroolek aset leidis, leiame, et kõigi $64$ mikrooleku esinemissagedus on üks ja seesama. Seega viibib süsteem keskmiselt sama kaua igas $64$ mikroolekus.

Kõik mikroolekud on küll võrdse tõenäosusega, kuid kuna eri konfiguratsioonides on erinev arv mikroolekuid, siis konfiguratsioonid ei ole ühesuguse tõenäosusega. Tabelis 20-1 on konfiguratsioon $IV$ oma 20 mikroolekuga kõige tõenäosem konfiguratsioon, selle tõenäosus on $20/64=0,313$. See tulemus tähendab, et süsteem viibib konfiguratsioonis $IV$ $31,3$ ajast. Konfiguratsioonid $I$ ja $VII$, mille korral kõik molekulid asetsevad konteineri ühes pooles, on vähima tõenäosusega, kummalgi $1/64=0,016$ ehk $1,6$. Pole üllatav, et kõige tõenäosem konfiguratsioon on selline, kus molekulid on konteineri kahe poole vahel jagatud võrdselt, sest seda võib oodata soojusliku tasakaalu korral. Üllataval kombel on mingi, kuigi väike tõenäosus ka selleks, et kõik molekulid on kogunenud konteineri ühte poolde ja teine pool on tühi.

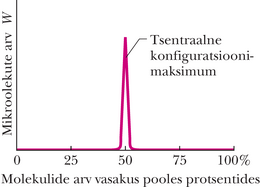
Suurte $N$ väärtuste korral on mikroolekute arv tohutu, kuid peaaegu kõik mikroolekud kuuluvad konfiguratsioonidesse, milles molekulid on võrdselt konteineri kahe poole vahel jagatud, nagu kujutatud joonisel 20-18. Kuigi gaasi temperatuur ja rõhk osutuvad mõõtmisel konstantseteks, loksub gaas pidevalt nii, et molekulid „külastavad” ühesuguse tõenäosusega kõiki võimalikke mikroolekuid. Ent kuna nii vähe mikroolekuid asub väljaspool joonisel 20-18 kujutatud väga kitsast tsentraalset konfiguratsioonimaksimumi, siis võib üsna kindlalt eeldada, et gaasi molekulid on alati võrdselt konteineri kahe poole vahel jagatud. Edasises saame näha, et selle konfiguratsiooni entroopia on kõige suurem.