Voog

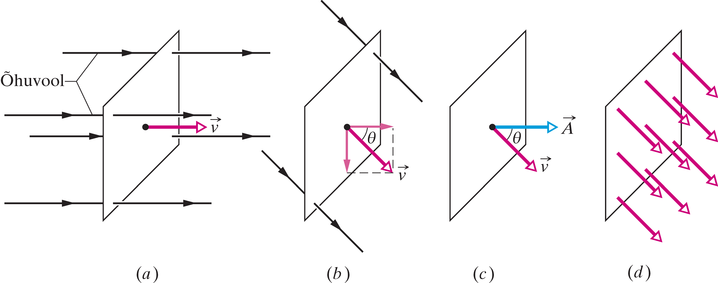
Joonisel 23-2a on kujutatud kiirusega $\to v$ liikuvat laia ühtlast õhuvoolu voolamas läbi väikese nelinurkse ava $A$ . Tähistagu $Φ$ voolu ruumkiirust (ruumala ajaühikus), millega õhk voolab läbi ava. See kiirus sõltub nurgast kiiruse $\to v$ ja ava tasandi vahel. Kui $\to v$ on risti ava tasandiga, siis on $Φ$ võrdne korrutisega $v A$ .

JOONIS 23-2 (a) Kiirusega $\to v$ liikuv ühtlane õhuvool on risti nelinurkse avaga, mille pindala on $A$ . (b) Kiiruse $\to v$ ava pinnaga risti olev komponent on $v cos θ$ , kus $θ$ on nurk kiiruse $\to v$ ja pinnaga risti oleva sirge vahel. (c) Pinnavektor $A$ on risti ava pinnaga ja moodustab kiirusvektoriga $\to v$ nurga $θ$ . (d) Kiirusväli, mis lõikab ava pinda.

Kui aga $\to v$ on paralleelne ava tasandiga, siis õhk ei voola üldse läbi ava ja seega on $Φ$ võrdne nulliga. Mingi vahepealse nurga $θ$ korral sõltub voog $Φ$ kiiruse $\to v$ sellest komponendist, mis on risti ava tasandiga (Joonis 23-2b). Kuna see komponent võrdub $v cos θ$ , siis on voo ruumkiirus läbi ava võrdne

(23-1)

Φ = (v cos θ) A

Selline pinda läbiv voolukiirus on voo üheks näiteks, antud juhul on tegemist ruumvooga.

Enne, kui käsitleda voogu elektrostaatikas, on vaja viia valem 23-1 vektorkujule. Selleks defineerime esmalt pinnavektori $\to A$ kui vektori, mille suurus on võrdne pinna pindalaga (antud juhul ava pindalaga) ja mille suund on risti pinnatasandi suunaga (Joonis 23-2c). Nüüd saame valemi 23-1 anda õhuvoolu kiirusvektori $\to v$ ja pinnavektori $\to A$ skalaarkorrutisena:

(23-2)

Φ = v A cos θ = \to v \cdot \to A

kus $θ$ on vektorite $\to v$ ja $\to A$ vaheline nurk.

skalaarkorrutis.Termin ’voog’ on seotud sõna ’voolama’ tähendusega. See tähendus on mõttekas siis, kui kõneleme õhu voolamisest läbi ava. Kuid valemit 23-2 saab vaadelda ka abstraktsemalt. Selleks iseloomustame ava läbiva õhuvoolu igat punkti vastava kiirusvektoriga (Joonis 23-2d). Kõik need vektorid kokku moodustavad kiirusvälja ja nüüd saab valemit 23-2 tõlgendada kui kiirusvälja voogu läbi ava. Sellises tõlgenduses ei tähenda voog enam mingi materiaalse aine voolamist läbi pinna, vaid on pinna ja sellel paikneva vektorvälja