Ideaalse gaasi rõhk

Impulsi jäävuse seaduse abil saab kirjeldada ka gaasides toimuvaid protsesse. Hõredat gaasi võib ette kujutada süsteemina, mis koosneb paljudest korrapäratult liikuvatest mõõtmeteta molekulidest, mis mõjutavad anumat ning muid kehi vaid elastsete põrgete kaudu. Niisugust gaasi mudelit nimetatakse ideaalseks gaasiks.

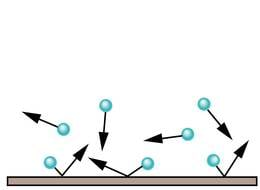
Ideaalne gaas koosneb elastselt põrkuvatest mõõtmeteta molekulidest

Kui sellise gaasi iga molekuli mass on m₀ ja kiirus v, omavad need kõik impulssi p₀ = m₀v. Absoluutsellt elastsel põrkel vastu mingit pinda muutub liikumine vastassuunaliseks ja uus impulss on –m₀v. Molekuli impulsi muut on siis Δp₀ = m₀v – (–m₀v) = 2 m₀v.

Lühikese ajavahemiku Δt jooksul saavad mingi pinna poole liikuvatest osakestest sellega põrkuda vaid need, mis ei asu kaugemal kui vahemaa s = v Δt. Kui pinna suurus on S, asuvad need molekulid kõik piirkonnas, mille ruumala V = S•s = SvΔt.

Gaaside iseloomustamiseks kasutatakse molekulide kontsentratsiooni (tähis n). See suurus näitab osakeste arvu ruumalaühikus. Molekulide koguarvu N saab leida, kui korrutada kontsentratsioon ruumalaga: N = nV.

Gaasi rõhk on tingitud impulsi muutusest molekulide põrgetel

Eelnevalt leidsime ruumala, milles asuvad molekulid võiksid aja Δt jooksul pinnani jõuda. Nende molekulide arv on N = nV = nSvΔt. Tegelikult on põrkuvate molekulide arv väiksem. Range tuletuskäik näitab, et kolmemõõtmelises ruumis on molekulide kaootiline liikumine oma mõju poolest samaväärne sellega, kui nad liiguksid vaid kolmes sõltumatus ristsihis. Konkreetse pinnaga ristuvas sihis liikuvaid osakesi on kolmandik koguarvust. Pinnale lähenevad neist vaid pooled, ülejäänud eemalduvad. Põrkuda saavaid molekule on seega vaid kuuendik koguarvust. Kui igal põrkel muutub molekuli impulss Δp₀ võrra, siis kõikide põrkuvate molekulide impulsside muut kokku on

Δ p = Δ p_{0} \frac{N}{6} = \frac{2}{6} m_{0} v n S v Δ t

Sellest seosest saame avaldada impulsi muutumise kiiruse, mis on teatavasti võrdne jõuga:

\frac{Δ p}{Δ t} = \frac{1}{3} m_{0} n v^{2} S = F

Jagades selle jõu pindalaga S, saamegi rõhu, mida ideaalne gaas avaldab selles asuvatele kehadele:

P = \frac{1}{3} m_{0} n v^{2}

(P ei tähista siin impulssi vaid rõhku)

Mehaanika kursuses me sellel valemil pikemalt ei peatu. Tulemus on leidnud katselist kinnitust ning see näitab, et impulsi jäävuse seadust saab füüsikas rakendada ka väljaspool mehaanikat.