Joonistame arvtelje, lööme sinna naelaga keskele nulli, võtame nöörijupi ning tähistame kaks arvu a ja –a. Need arvud on nullpunktist samal kaugusel. Seda kaugust nullpunktist nimetatakse arvu absoluutväärtuseks.

Seega arvude 1 ja –1 absoluutväärtus on 1, kuna nad asuvad mõlemad nullpunktist täpselt ühiku kaugusel, ning samamoodi on arvude π ja –π mõlema absoluutväärtus π.

Kuna arvu absoluutväärtus tähistab kaugust, ei saa ta muidugi olla negatiivne.

Arvu absoluutväärtust tähistatakse, asetades arv püstkriipsude vahele. Näiteks |1| = 1 ja |– 1| = 1. Võibki mõelda, et kriipsud suruvad miinuse kokku.

Matemaatiliselt võib arvu absoluutväärtuse defineerida nii:

kui x on positiivne, siis |x| = x,

kui x on negatiivne, siis |x| = –x,

kui x on võrdne nulliga, siis |0| = 0.

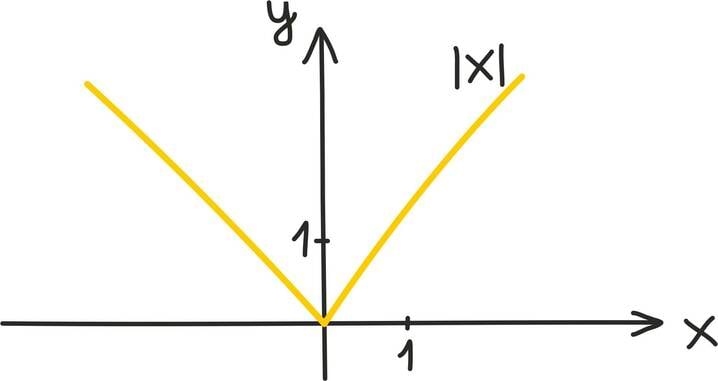
Kui leiame iga reaalarvu jaoks tema absoluutväärtuse, saame järgmise graafiku – funktsiooni |x| graafiku.

Oluline on võibolla ka märgata, et kuigi defineerisime arvu absoluutväärtuse kui tema kauguse nullist, võime absoluutväärtuse abil kirjeldada tõesti kõikide arvude vahelisi kauguseid. On ju arvude x ning y vahelise kauguse leidmine täpselt võrdne nende vahe x – y (või miks ka mitte y – x) kaugusega nullpunktist.