Võrratuse lahendamine tähendab täpselt sama, mida võrrandi lahendaminegi – tuleb leida antud tingimustega sobivad muutuja väärtused [lk 176].
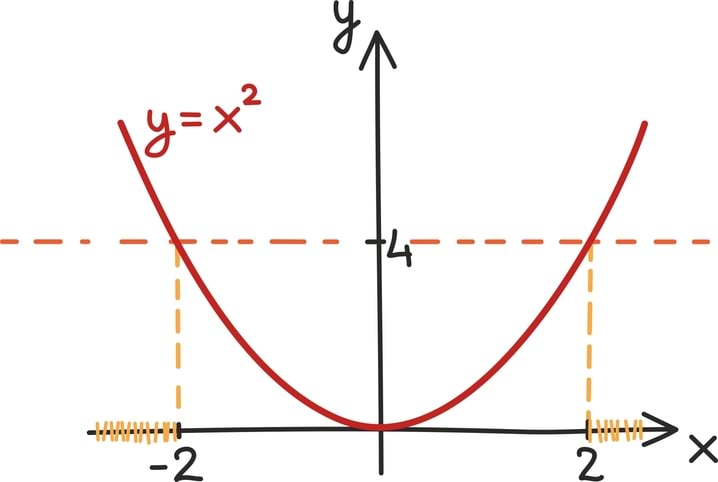
Näiteks kui tahtsime leida arve, mille ruut oli võrdne 4-ga, saime võrrandi: x2 = 4. Samamoodi võime otsida arve, mille arvuruut on 4-st suurem. Seda kirjeldab võrratus: x2 > 4.
Võrratuste lahendamisel on tihti kasulik mõelda geomeetriliselt – üritame kogu võrratuse taandada mõne funktsiooni graafiku uurimisele.
Ülaltoodud võrratuse korral näeme, et kõik otsitavad arvud peavad olema kas kahest suuremad või miinus kahest väiksemad, sest muudel juhtudel on ruutfunktsiooni y = x2 graafik 4-st madalamal.
Sama strateegia toimib ka keerulisemate võrratuste puhul. Näiteks oletame, et küsitakse, milliste reaalarvude x jaoks on
Kasutades võrratuse omadusi võime selle võrratuse ümber viia kujusse
Sellises kujus vastab võrratus küsimusele: millal asub kuupfunktsioon x-teljest üleval pool?
Kuupfunktsiooni graafik teeb kokku maksimaalselt kaks pööret, aga sellest räägime pikemalt osa 6 juures [lk 266].
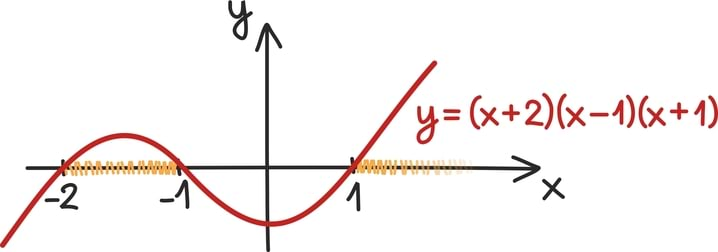
Kuupfunktsiooni oskame umbkaudu joonistada niipea, kui teame ta nullkohti [lk 269]. Seega tegurdame vasemat poolt ja saame samaväärse võrratuse (x + 2) (x – 1) (x + 1) > 0. Nüüd võime vastuse välja lugeda joonistades umbkaudselt kuupfunktsiooni y = (x + 2) (x - 1) (x + 1) graafiku.
Meile sobivad kõik arvud vahemikus (–2, –1) ning kõik ühest suuremad arvud:
Graafiline meetod põhineb sisuliselt funktsioonide graafikute võrdlemisel. Oleksime võinud eelnevalt ka lihtsalt võrrelda funktsioonide x3 + 2x2 ja x + 2 graafikuid, aga lihtsam oli teisendada võrratust nii, et üks funktsioon oli kuuppolünoom ja teine lihtne nullfunktsiooni, mille graafikuks on siis x-telg ise.
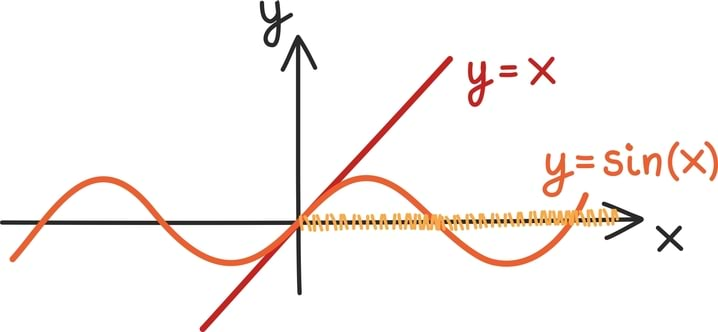
Mõnikord peame aga tõesti joonistama välja kaks erinevat funktsiooni. Näiteks näeme graafikult, et x ≥ sin(x) iga mittenegatiivse x-i jaoks.
Selle fakti range tõestus kasutab tuletist [lk 320] ja põhineb täpselt graafikult saadud intuitsioonil: kohal 0 on mõlemad funktsioonid võrdsed ning edasi kasvab funktsioon y = x kiiremini kui funktsioon y = sin(x).
Kuna võrdusjuht on mingis mõttes võrratuse piirjuhuks, võime võrratuste lahendamise taandada tihti võrrandite lahendamisele. Mingis mõttes tegime seda ka kogu eelnenud arutelus: leidsime geomeetriliselt, kus on mingid lõikepunktid, ning otsustasime, kummale poole jäävad siis võrratuse lahendid. Lõikepunktid ise aga tähistasidki võrrandite lahendeid ja piirasid võrratuse lahendite ala. Just selle seose tõttu saime ka tegelikult mobiilioperaatorite küsimusele ainult võrrandite raames vastuse leida.