Mõned levinud võrratused

Nii nagu koolist on hästi teada, et õpetaja on alati targem kui õpilane, kehtivad ka teatud võrratused väga paljude erinevate arvude või elementide jaoks. Näiteks kehtivad mõned võrratused absoluutselt kõikide positiivsete reaalarvude jaoks või kõikide ühest suuremate reaalarvude jaoks või kõikvõimalike kolmnurkade jaoks. Loetleme ja selgitame neist siinkohal mõnda.

Reaalarvu ruut

Kõige tuntum võrratus on ilmselt järgmine: iga reaalarvu ruut on mittenegatiivne ehk a² ≥ 0. Võrdus kehtib muidugi parajasti juhul, kui a on võrdne nulliga. Miks see ikkagi on nii?

Nulli puhul on muidugi asi selge, on ju nulli ruut jällegi null.

Ka positiivsete arvude puhul pole asi palju keerulisem: a² on ju täpselt küljega a ruudu pindala ning ruudu pindala peabki positiivne olema.

Iga negatiivse arvu võime aga kirjutada kujul –a = (–1) · a, kus a on ise positiivne. Sel juhul võime kirjutada

{(- a)}^{2} = (- a) \cdot (- a) = (- 1) \cdot (- 1) \cdot a \cdot a = a^{2}

ning tulemus on jällegi positiivne.

Kumb on suurem, arv või tema ruut?

Võibolla kõlab see alguses natuke mitteintuitiivselt, aga arvu ruut ei ole mitte sugugi alati suurem kui arv ise. Negatiivse arvu ruut on muidugi alati temast suurem, sest eelneva põhjal on arvuruut ise alati positiivne.

Samuti, kui positiivne reaalarv on ühest suurem, siis on ta ruut arvust suurem. Kui aga positiivne reaalarv on ühest väiksem, siis on ta ruut arvust väiksem:

\begin{matrix} a^{2} > a, k u i a > 1 v ˜ o i a < 0 a^{2} < a, k u i 0 < a < 1 a^{2} = a, k u i a = 0 v ˜ o i a = 1 \end{matrix}

Ka seda pole väga raske tõestada – teame ju, et võime iga võrratust positiivse täisarvuga läbi korrutada:

korrutades võrratuses a >1 mõlemad pooled a-ga, saame võrratuse a²> a,
korrutades võrratuses a < 1 mõlemad pooled a-ga, saame võrratuse a² < a.

Aritmeetiline ja geomeetriline keskmine

Arvude aritmeetiline keskmine tuleb esile üsna tihti: näiteks arvutatakse välja keskmist hinnet, eksamitulemuste keskmist või rahva keskmist vanust. Selle jaoks liidetakse lihtsalt kõik uuritavad tulemused kokku ja jagatakse summa tulemuste arvuga:

A = \frac{a_{1} + a_{2} + \dots + a_{n}}{n}

Keskmistada võib aga teisiti: võib kõik tulemused kokku korrutada ning siis võtta nendest nii mitmes juur, kui palju tulemusi oli.

A = \sqrt[n]{a_{1} \cdot a_{2} \cdot \dots \cdot a_{n}}

Geomeetriline keskmine tuleb esile näiteks televiisorite kuvasuhete määramises. Vana kinostandard oli kuvasuhe 2,39:1 (pilt on 2,39 korda laiem) ning vana televiisor näitas filme suhtes 4:3. Nende kahe standardi vahel kompromissi leidmiseks kasutati geomeetrilist keskmist ning saadi tulemuseks 16:9 standard. Geomeetrilise keskmise kasutamine võimaldas saavutada olukorra, kus mõlemaid proportsioone „muudeti” ühepalju.

Nii aritmeetiline kui geomeetriline keskmine on ka seotud vastavanimeliste jadadega [lk 128]. Nimelt on aritmeetilise jada kolmest järjestikusest liikmest keskmine äärmiste aritmeetiliseks keskmiseks ning täpselt sama juhtub ka geomeetrilises jadas, kasutades geomeetrilist keskmist.

Üks tuntud võrratus väidab, et kahe mittenegatiivse reaalarvu aritmeetiline keskmine on vähemalt sama suur kui kahe arvu geomeetriline keskmine. Ehk:

\frac{a + b}{2} \geq \sqrt{a b}

Kuidas seda tõestada?

Vaatame arvu

{(\sqrt{a} - \sqrt{b})}^{2}

Kuna tegemist on arvuruuduga, siis on ta mittenegatiivne. Avades sulud, saame

a + b - 2 \sqrt{a b} \geq 0

ehk tõesti

\frac{a + b}{2} \geq \sqrt{a b}

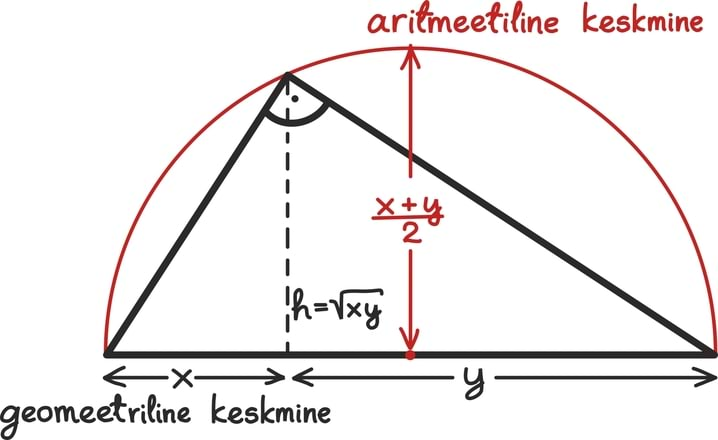
Graafiliselt võib aritmeetilisest ja geomeetrilisest keskmisest ning nendevahelisest võrratusest mõelda järgnevalt:

Tõestus vajaks natuke kolmnurkade ja trigonomeetriaga mängimist. Huvitunud lugeja võib seda proovida näiteks peale trigonomeetria peatüki läbimist [lk 205].

Kuigi meie tõestasime siin ainult, et kahe arvu aritmeetiline keskmine on suurem geomeetrilisest keskmisest, siis tegelikult kehtib väide mistahes paljude arvude kohta. Suvalise mittenegatiivse arvu aritmeetiline keskmine on suurem kui geomeetriline keskmine. Seda on siiski juba pisut keerulisem tõestada.

Lühim murdjoon

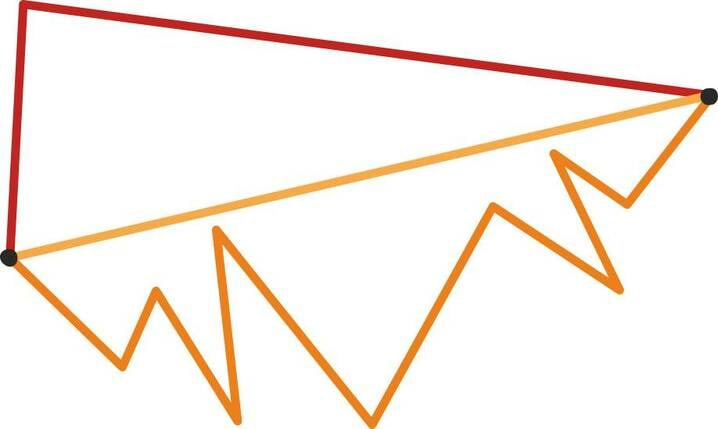
Lõpetame peatüki ühe väga lihtsa geomeetrilise võrratusega. See väidab, et kahe punkti vahelistest murdjoontest on vähima pikkusega neid punkte ühendav sirglõik.

Sellest võrratusest järeldub kohe näiteks tuntud kolmnurga võrratus: kolmnurga iga kahe küljepikkuse summa on pikem kui kolmas külg. See lihtne väide osutub järelikult üsna sisukaks.