Kasutades täisnurkse kolmnurga jaoks defineeritud trigonomeetrilisi põhiseoseid, võime omavahel siduda nurkasid ja külgi ka mittetäisnurksetes kolmnurkades.
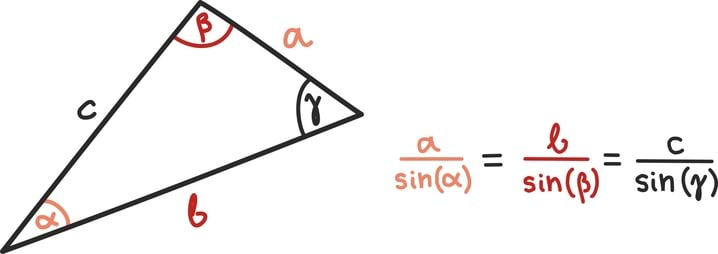
Tuntuim selline seos on ilmselt siinusteoreem, mis väidab, et iga nurga vastaskülje ja selle nurga siinuse suhe on võrdse väärtusega. Kuigi intuitiivselt on selge, et nurgad ja külgede suhted peavad olema omavahel seotud, siis siinusteoreemi täpne sõnastus on siiski üllatavalt leidlik ja lihtne:
Enne kui siinusteoreemi tõestama asume, räägime mõnest tema matemaatilisest rakendusest.
Mõned siinusteoreemi rakendused
Esimese rakendusena aitab siinusteoreem leida puuduvaid elemente kolmnurgas – tema abil võime teadmised nurkadest pöörata teadmisteks küljepikkuste kohta ja vastupidi.
Samuti võime siinusteoreemist vähemalt teravnurkse kolmnurga jaoks üsna kergesti järeldada midagi päris ilusat: kolmnurga pikemate külgede vastas on suuremad nurgad.
Tõepoolest, siinusteoreemist teame, et
Nüüd kui küljepikkuste vahel kehtib a > b, siis peab kehtima ka sin(α) > sin(β). Samas aga nägime ennist, et teravnurksete nurkade jaoks on siinus kasvav funktsioon. Seega järeldame, et nurk α peab nurgast β suurem olema. Ehk suurema nurga vastas on ka suurem külg.
Siinusteoreemi tõestus teravnurkse kolmnurga jaoks
Lugeja võib paberi, pastaka ja natukese kritseldamisega veenduda, et siinusteoreem ei ütle täisnurkse kolmnurga jaoks midagi uut – kogu seos järeldub siinuste definitsioonist.
Mittetäisnurkse kolmnurga jaoks on siiski tegemist millegi uue ja põnevaga, mida on vaja ka tõestada, teisisõnu selgitada meile juba varasemate teadmiste abil. Miks muidu peaksime seda uskuma?
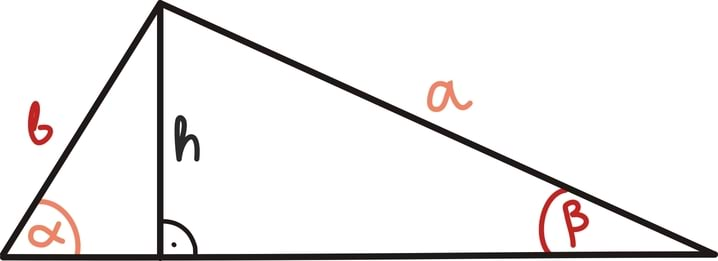
Kuidas siis argumenteerida? Tuletame meelde, et siinus on defineeritud täisnurkse kolmnurga kaudu. Seega tuleks kuidagi konstrueerida täisnurkne kolmnurk, milles neid definitsioone kasutada võiksime.
Üks võimalus on lihtsalt tõmmata kõrgus. Nii jagame algse kolmnurga kaheks täisnurkseks kolmnurgaks. See tundub juba päris hea algusena, sest nende täisnurksete kolmnurkade üks külg on ju lisaks veel võrdne – just seesama külg, mille abil saame nurga siinust välja kirjutada.
Seega kirjutamegi lihtsalt välja mõlemast kolmnurgast siinuse definitsiooni:
Avaldades mõlemast avaldisest kõrguse h, näeme, et h = b sin(α) ja samuti h = a sin(β)
Seega kehtib ka b sin(α) = a sin(β) ehk
Samamoodi võiksime muidugi ka tõmmata mõne teise kõrguse ja nii näidata kõikide suhete võrdsust.
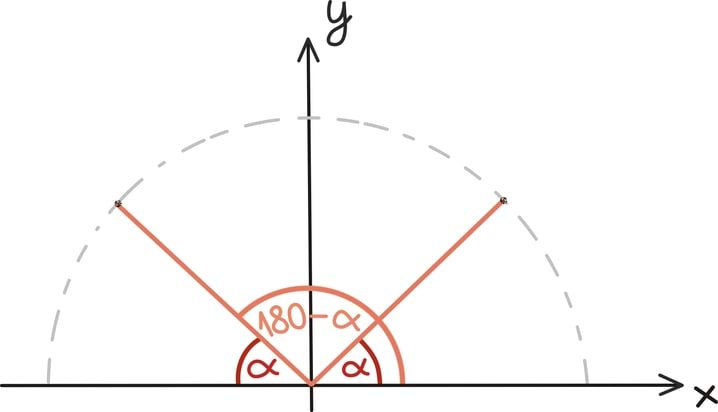
Nürinurkse kolmnurga puhul satub kõrgus küll kolmnurgast välja, aga see ei põhjusta probleeme. Nimelt kui vaadata hoolikalt siinusfunktsiooni definitsiooni suvalise nurga jaoks, näeme, et sin(α) = sin(180º – α). Tõepoolest, mõlemad haara otspunktid lõikavad ju ühikringjoont samal kõrgusel.
Siinusteoreemi laiendus
Tuleb välja, et tegelikult võib siinusteoreemi veel laiendada.
Nimelt on teada ka selle iga vastaskülje ja nurga siinuse suhte täpne väärtus – see on alati võrdne kolmnurga ümberringjoone diameetri pikkusega. Seega võime, kasutades ikka samu vanu tähiseid nurkade külgede jaoks ning tähistades kolmnurga ümberringjoone raadiuse R-iga, kirjutada siinusteoreemi täiskujul välja järgnevalt:
Sellel korral on tõestus pisut kavalam ja jätame ta huvitunutele nuputamiseks või järele pärimiseks.