See alapeatükk on skeptilisele ja huvitunud lugejale, kes ei taha uskuda, et pendel on seotud just täpselt siinuse ja koosinusega, mitte mõne muu perioodilise funktsiooniga.

See on igati õigustatud kahtlus!

Õnneks annavad füüsika ja matemaatika käsikäes siiski hea põhjendatud vastuse. Lihtsuse mõttes käsitleme küll siin peatükis hoopis elastset vedru, aga situatsioon ja ideestik on täpselt sama:

• meil on üks keha
• mida liigutab üksainus jõud,
• mis surub objekti tagasi tasakaaluasendisse,
• aga kahjuks liiga tugevasti ning keha jääb võnkuma tasakaaluasendi ümber.

Elastse vedru korral on mõjuvaks jõuks elastsusjõud. Inglise füüsik Hooke tegi 17. sajandil hoolega katseid ja veendus, et mida pikemalt on vedru välja venitatud, seda suurem jõud tõmbab teda kokku ning vastupidi, mida rohkem vedru on kokku surutud, seda suurem jõud lükkab teda jälle lahti.

Hooke oli hoolikas sell ja ta mõõtis ka täpselt välja, kuidas see jõud täpselt vedru väljavenitusest või kokkusurutusest sõltub. Ta tegi kaks järeldust:

• jõud on erinevatest materjalidest vedrude jaoks erinev,
• jõud sõltub täpselt ühtemoodi vedru pikkuse muudust – alati võrdeliselt.

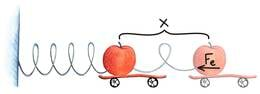
Tähistame nüüd vedru suurusemuutu tasakaaluasendi suhtes x-ga (positiivse x-i korral on vedru välja veninud, negatiivse korral kokku surutud) ning keha materjali jäikust iseloomustavat tegurit k-ga. Sel juhul väidab Hooke’i seadus, et vedru algkujusse kiskuvat elastsusjõudu F_e võib igal ajahetkel t kirjeldada valemiga

Samaaegselt oli Hooke’i kaasaegne ja rahvuskaaslane Newton leidnud veelgi üldisemaid printsiipe meid ümbritseva maailma kirjeldamiseks.

Ta märkas, et kui kehale mõjub mingi jõud, siis keha kiirendus – see, kuidas keha liikumiskiirus muutuma hakkab, – sõltub täpselt võrdeliselt mõjuvast jõust.

Veelgi enam, ta avastas, et mõõtes ka keha massi, võib ta täpselt kirjeldada, kuidas jõud keha kiiruse muutuma paneb: tähistades keha kiirendust a-ga, tema massi m-iga ning kehale ajahetkel t mõjuvat kogujõudu F(t)-ga, võib Newtoni teise seaduse välja kirjutada kujus:

Meie olukorras on ainus vedrule mõjuv jõud igal hetkel antud täpselt eeltoodud elastsusjõuga, mis tema kuju taastada üritab. Gravitatsiooni võime näiteks lihtsalt eirata, kuna horisontaalset liikumist ta ei mõjuta.

Seega võime kirjutada, et vedrule mõjub kogujõud F = F_e, ning valemitest asendades saame

Nii on liikumine igal ajahetkel t kirjeldatud võrrandiga

Selles võrrandis on peidus kaks arvkonstanti m ja k, mis sõltuvad keha omadustest; a(t) ja x(t) kirjeldavad aga igal ajahetkel vastavalt vedru venituse kiirendust ja väljavenituse suurust.

Ometigi on intuitiivselt üsna selge, et ühe objekti kiirendus – tema kiiruse muutumine – on juba olemuslikult ka seotud tema asupaigaga.

Seda seost toob täpsemalt esile tuletise peatükk [lk 320]. Nimelt kiirenduse näol on tegemist läbitud teepikkust või teisisõnu vaadeldava keha asukohta kirjeldava funktsiooni teise tuletisega. Isegi kui tuletis tundub ohtliku sõnana, ei ole selles suurt midagi keerulist – funktsiooni esimene tuletis näitab lihtsalt, kui kiiresti funktsiooni väärtus muutub, ning funktsiooni teine tuletis näitab, kui kiiresti see muutumine ise muutub. Nii ongi näiteks kiirus teepikkuse esimene tuletis ning kiirendus tema teine tuletis.

Seega ütleb meie võrrand, et igal hetkel t on vedru venituse muutumise kiirendus võrdeline tema kogumuutusega:

Võime neid iga ajahetke kohta antud võrrandeid vaadata ka ühe seosena üle kogu aja korraga – seosena ajast sõltuva funktsiooni ning tema teise tuletise vahel.

Sellist võrrandit, mis seostab funktsiooni ja tema tuletisi nimetatakse uhkelt diferentsiaalvõrrandiks – diferentseerimine tähendab ju lihtsalt tuletise võtmist. Nende lahendamine päris käkitegu pole, aga sel korral võib sellega siiski hakkama saada, kui meenutame trigonomeetriliste funktsioonide tuletisi.

Siinusfunktsiooni sin(t) tuletiseks on cos(t) ning sarnasel on koosinusfunktsiooni cos(t) tuletiseks – sin(t). 

Need kaks teadmist kokku pannes näeme, et siinusfunktsiooni teine tuletis on – sin(t). Seega rahuldab ta etteantud diferentsiaalvõrrandit, juhul kui

Saamegi ilusa siinuskujulise liikumise, mille periood on täpselt 2π.

Kui aga

on mõne teise väärtusega, peame vastuse leidmiseks muutma oma siinuslaine sagedust kas aeglasemaks või kiiremaks.

Tuleb välja, et üldjuhul on sobivaks lahendiks

Siingi võiks veel nuriseda – sarnaselt sobib ju lahendiks ka koosinusfunktsioon ning veelgi enam, ka koosinus ja siinusfunktsiooni summa! Vedru võngub ju aga ometigi täpselt ühtemoodi, mitte mitut moodi korraga. Tõepoolest, selgub, et puhta siinus- või koosinusfunktsiooni määramiseks tuleb teha veel üks tähelepanek. Nimelt on vedru kiirus kõige suurema väljavenimise ja kokkusurutuse hetkel võrdne nulliga. See tuleneb energia jäävuse seadusest – neil hetkedel on kogu energia muundunud potentsiaalseks energiaks. Seda teadmist arvesse võttes on meie siinusfunktsioon juba üheselt määratud.

Loodame, et nüüd on ka skeptilisem lugeja veendunud, et vedru või ka pendli perioodilise liikumise kirjeldamiseks ei sobi sugugi mitte mingi suvaline siksak või muu perioodiline funktsioon. Sobib just meile juba teada ja tuntud siinusfunktsioon.