Integreerimine

Kui tuletis oli ajast sõltuva funktsiooni spidomeetriks ning näitas funktsiooni hetkelist muutumise kiirust, siis integraali tähendus on vastupidine: integraal leiab funktsiooni spidomeetri põhjal tema kogumuudu. Järgnevalt alustame integraali idee selgitamisest ja loodame jõuda lõpuks siiski ka integraali matemaatilise definitsioonini [lk 44].

Lugulaul

Kuna integraal ja tuletis on tihedalt seotud, alustame ka sarnase lugulauluga – kihutad mäest alla. Muidugi, nagu sissejuhatuses juba mainisime, on nüüd käes kevad ning suuskade asemel oleme andnud Sulle hoopis ratta. Lisaks on meil seekord käepärast spidomeeter ja tahame arvutada hoopis läbitud tee pikkust.

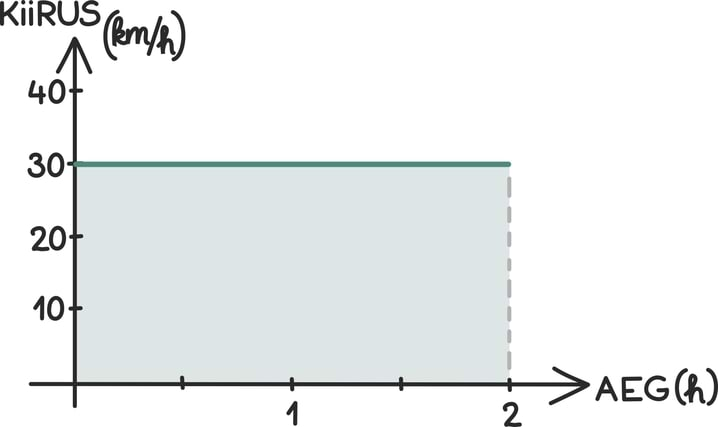
Kuidas seda teha? Oskame tee pikkust kiiruse ja aja abil leida siis, kui kiirus on konstantne. Sellisel juhul on ka kiiruse graafiku alla jääv kujund kenasti ristkülik ning pindala valem ühtib täpselt tee pikkuse leidmise valemiga: s = vt

Probleem on aga selles, et mäest alla veeredes kiirus aina suureneb. Seega kümnendaks sekundiks läbitud tee pikkuse leidmiseks ei piisa enam sellest, kui vaataksime spidomeetrit näiteks alles viimasel sekundil ning kasutaksime seda kiirust oma läbitud tee pikkuse leidmiseks. Probleemi lahendus on siiski üsna lihtne: jagame aja lühikesteks vahemikeks ehk vaatame spidomeetrit üsna tihedalt.

Idee peitub selles, et väga lühikese ajavahemiku jooksul kiirus väga ei muutu. Seega võime igas lühikeses ajavahemikus läbitud tee pikkuse leida üsna täpselt, kui korrutame lihtsalt ajavahemiku pikkuse ning spidomeetrilt saadud kiiruse. Liites seejärel kokku igas lühikeses ajavahemikus läbitud tee pikkused, saamegi päris täpse vastuse.

Nagu tuletisegi peatükis – mida väiksemad ajavahemikud võtame ehk mida tihedamalt spidomeetrit vaatame, seda täpsem on ka meie vastus. Seekord annab integraal selle täpse vastuse, mida otsime – täpse tee pikkuse – ja taas kord tulevad matemaatiliselt mängu ka piirprotsessid [lk 308]. Nagu hiljem näeme, on nad seekord ainult veidi keerulisemad kirja panna.

Kõike seda võib ette kujutada ka geomeetriliselt.

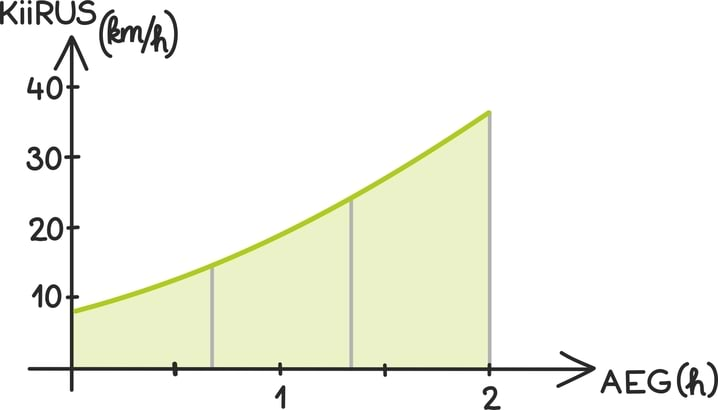
Esiteks, aja lühikesteks vahemikeks jagamine tähendab geomeetriliselt lihtsalt kiiruse graafiku alla jääva kujundi jagamist väikesteks tükkideks.

Teiseks, igas vahemikus tavalise teepikkuse valemi kasutamine tähendab, et iga väikese tüki pindala lähendame ristkülikukujulise tüki pindalaga.

Lõpuks liidame kõik need pindalad kokku.

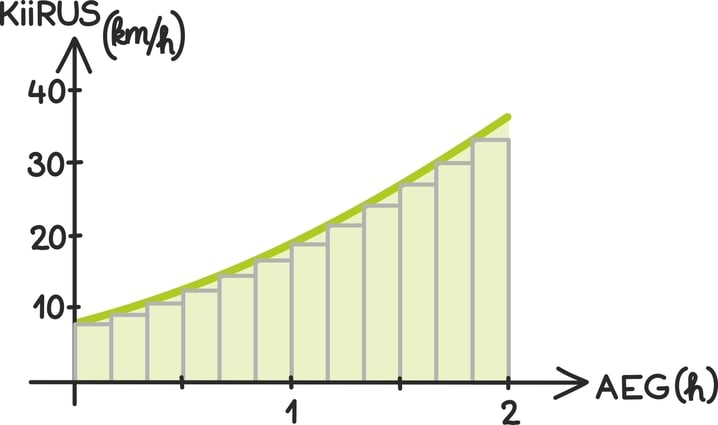
Joonist lähemalt vaadates on üsna selge, et mida väiksemad ajavahemikud, seda täpsem vastus. Kasutades ristkülikutega lähendamist, teeme iga väikese pindala arvutamisel teatava vea, aga mida väiksem vahemik, seda vähem oma hinnangus eksime.

Seega kokkuvõttes, täpne läbitud tee pikkus ongi kiirusfunktsiooni integraal ning omakorda on see antud kiirusfunktsiooni alla jääva kõvertrapetsi (nii nad seda kutsuvad...) pindalaga.

Taas kord on praktikas, spidomeetri abil täpse tee pikkuse ehk integraali leidmine võimatu – lõpmatult tihedalt ei ole võimalik spidomeetrit vaadata. Niipea kui meil on käest võtta matemaatiline kirjeldus, saame aga kohe asuda integreerima.

Konkreetne näide

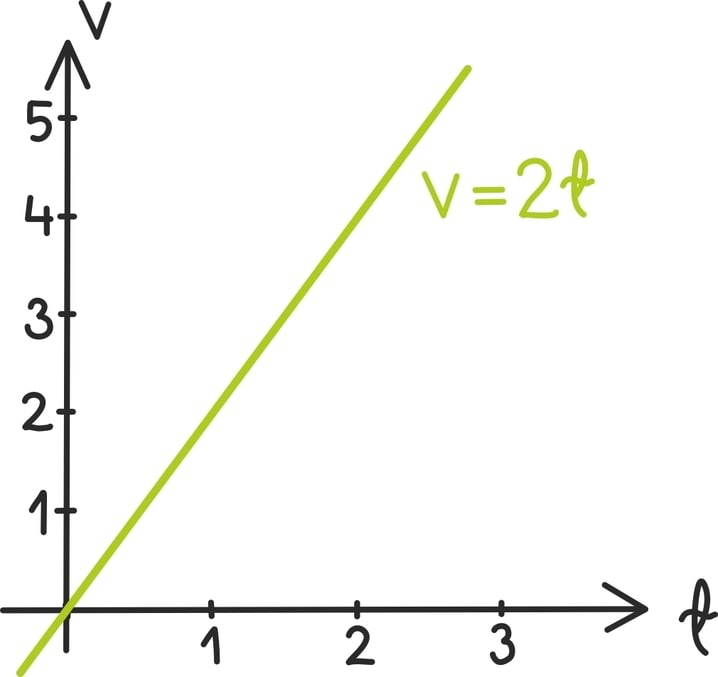
Täpsustame nüüd, et tuiskad rattaga jällegi alla meile juba tuntud ideaalsest mäest. Tuletame meelde ka tuletise peatükist, et sel juhul on Su kiirus ajas antud valemiga v = 2t. Kuna laskumised pole väga pikad, mõõdame jälle aega sekundites.

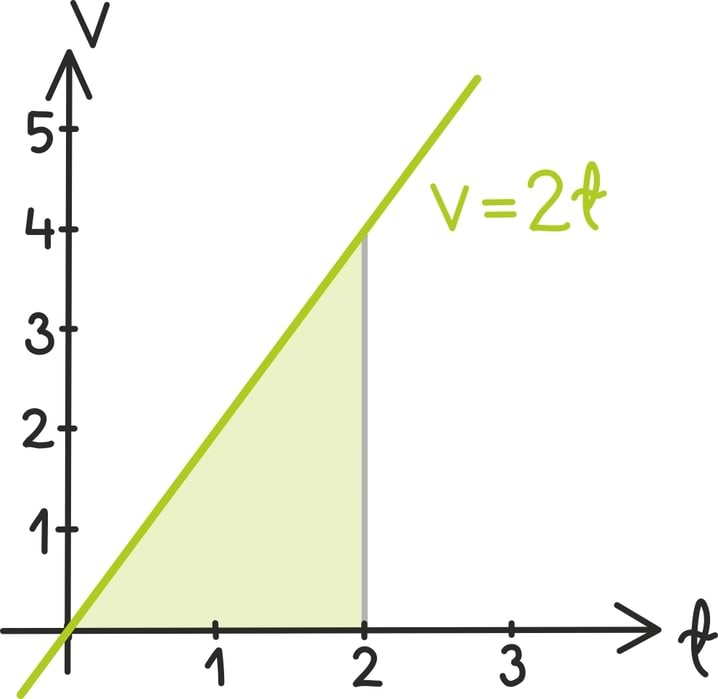
Nagu juba märkasime, võime kiiruse ja aja suhet kirjeldada graafiliselt:

Nii on kahe sekundi möödudes juba saavutatud kiirus 4 m/s. Kui tahame nüüd leida nende kahe sekundiga läbitud tee pikkust, peame lihtsalt leidma joone alla jääva kujundi pindala.

Kavalpead võivad kohe näha, et võime seda teha näiteks kolmnurga pindala valemist ning saada vastuseks

\frac{2 \cdot 4}{2} = 4 (m)

Teine ning levinuim viis selle integraali leidmiseks on kasutada seost tuletise ja integraali vahel – kuna integraal ja tuletis on teatud mõttes pöördoperatsioonid, võime integraali leidmise taandada tuletise teadmisele ning vastupidi. Sellest pikemalt integraali ja tuletise peatükis [lk 352].

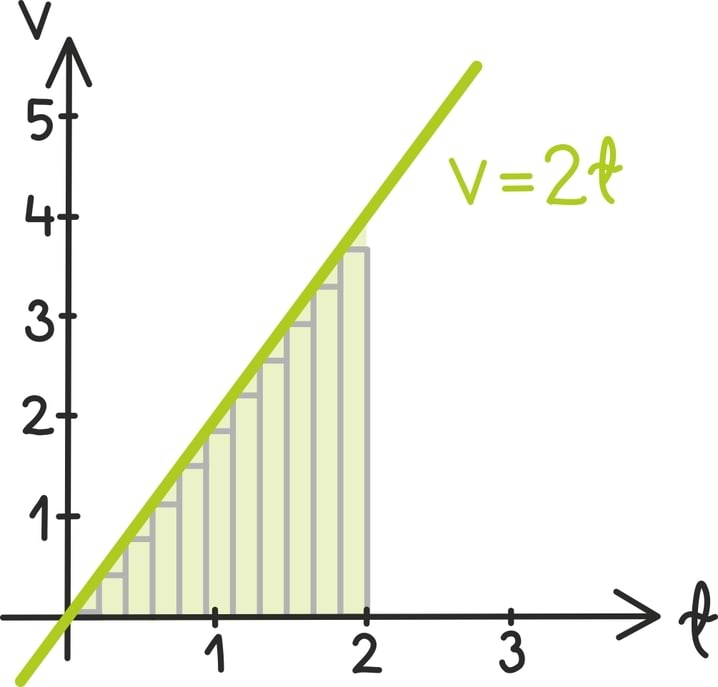
Viimaks näitame aga, kuidas integraali leida näppudel, kiiruse graafiku alla jäävat kujundit väikesteks tükkideks jagades ning nende pindalasid kokku liites, ehk lühemalt – kuidas käsitsi integreerida:

Jagame oma lühikese ajavahemiku 2 sekundit n väikeseks vahemikuks, millest iga pikkus on täpselt

\frac{2}{n}

Vahemik i ulatub siis ajahetkest

\frac{2 (i - 1)}{n}

kuni ajahetkeni

\frac{2 i}{n}

Igas selles vahemikus hindame kiirust vahemiku lõppkiiruse abil.

Kasutades valemit v = 2t, on meie hinnang vahemiku i lõppkiiruse jaoks

\frac{4 i}{n}

Selles vahemikus läbitakse seega hinnanguliselt tee pikkus

\frac{8 i}{n^{2}}

Liites need väikesed tee pikkused kokku, saame

S_{n} = n \sum i = 1 \frac{8 i}{n^{2}} = \frac{8}{n^{2}} n \sum i = 1 i

See kõverik on juba varem kirjeldatud [lk 50] summa märk, aga meeldetuletuseks kirjutame summa ka pikalt välja:

S_{n} = \frac{8}{n^{2}} n \sum i = 1 i = \frac{8 i}{n^{2}} (1 + 2 + \dots + n + n - 1 + n)

Me juba teame (näiteks aritmeetilise jada summavalemist), et

n \sum i = 1 i = \frac{n (n - 1)}{2}

seega

S_{n} = \frac{8}{n^{2}} \cdot \frac{n (n - 1)}{2} = 4 \frac{n - 1}{n} = 4 - \frac{4}{n}

Meie hinnang sõltub selgelt ajavahemike arvust n liikme

\frac{4}{n}

kaudu.

Samas kui n viia lõpmatult suureks, muutub see liige imepisikeseks ning piirprotsessis kaob hoopis. Seega saame kogu tee pikkuseks ehk integraaliks vastuse 4. Ühikud tuleks muidugi eraldi juurde sobitada, et saada nagu enne vastus 4 meetrit.

Integraali tähis ja matemaatiline kirjapanek

Matemaatilisemaks kirjelduseks on kunstilembesed matemaatikud integraalile andnud ka tähise, mis on lihtsalt üks välja venitatud s.

\int

S on ta just sellepärast, et integraal ise on lõputult paljude asjade kokkuliitmisel justkui üks välja venitatud summa.

Sellises kõverikus endas on aga veel üsna vähe informatsiooni. Et teda mõistlikult kasutada, on veel vaja ära märkida, mida me integreerime, mille suhtes ja kui pikas vahemikus.

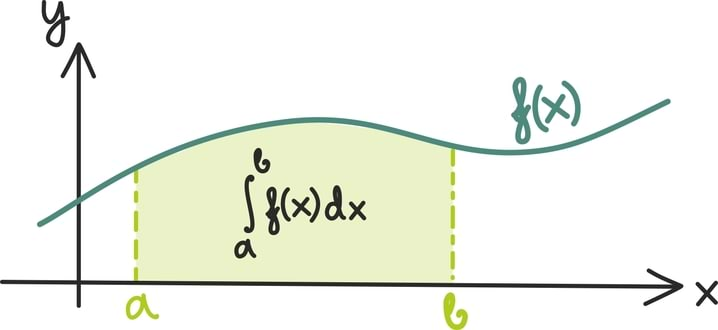
Kui meil on antud mingi muutumist kirjeldav funktsioon ƒ(x), siis tema integraali või kogumuutust x-i suhtes vahemikus [a, b] tähistame:

\int_{a}^{b} f (x) d x

Graafiliselt on see integraal vastavuses siis x-telje, joonte x = a ning x = b ja funktsiooni ƒ(x) graafiku vahele jääva piirkonna pindalaga:

Ülaltoodud näites integreerime kiirust v(t) aja t suhtes, vahemikus ajahetkest 0 kuni ajahetkeni 2, sel juhul võime integraali kirja panna kujus:

\int_{0}^{2} v (t) d t

Meie konkreetse näite korral leidsime siis järgmise integraali:

\int_{0}^{2} 2 t d t = 4

Kuhu jääb definitsioon?

Aga kuhu jääb integraali matemaatiline definitsioon?

Lihtne vastus: suur osa täpsest definitsioonist jääb ülikooli. Integraali mõistlikuks defineerimiseks tuleb olla päris hoolas.

Tuletame meelde, et integraal mõõtis spidomeetri põhjal tee pikkuse kogumuutu mingis vahemikus. Tema leidmiseks jagasime ahemiku väikesteks tükkideks ning leidsime muudu neis vahemikes. Liites need muudud kokku, saime hinnangu integraalile. Piirprotsessis, kus vahemikke oli aina rohkem ning nad olid aina lühemad, saimegi integraali enda.

Konkreetses näites kasutasime tee pikkuse leidmiseks ühepikkuseid ajavahemikke ning mõõtsime igas vahemikus kiirust ajavahemiku otspunkti põhjal.

Võttes sellest kõigest malli, võiksime matemaatiliselt defineerida, et integraal tähendab just seda, et jagame ajavahemiku järjest rohkemateks osadeks, valime alati pisikeste ajavahemike otspunktid ning arvestame neid tee pikkuse leidmiseks. Integraali saame piirprotsessis, kus n tormab lõpmatusse.

Sümbolite keelde tõlkides tähendaks see, et defineeriksime:

\begin{matrix} \int_{a}^{b} f (x) d x = = lim n \to \infty \frac{1}{n} (f (a + \frac{b - a}{n}) + f (a + 2 \frac{b - 2}{n}) + \dots + f (b)) \end{matrix}

Ent stopp! Siin teeme kaks üsna suvalist valikut. Esiteks on suvaline see, et jagame kogu vahemiku võrdseteks tükkideks. Teiseks, miks peaksime muutu hindama just vahemiku parema otspunkti põhjal?

Ühtegi väga head põhjust kummakski ei ole ja see peaks juba valvsaks tegema – kas me tegime õiged valikud? Kas teised valikud annaksid ikka sama integraali? Kas leidub mõni „õige” valik? Kas saab kuidagi üldisemalt integraali defineerida, nii et ei täpsustagi täpselt, kuidas vahemikke võtame ning millise punkti neis valime?

Kõik need on põnevad küsimused, kahjuks jäävad aga sellest raamatust juba kaugemale. Integraali rangeks defineerimiseks leidubki tegelikult mitu erinevat viisi intuitsiooni jääb aga alati samaks, selleks, mille ülalpool ka esile tõime. Kusjuures võibolla on ka oluline lisada, et konkreetsed siin tehtud valikud pole just parimad – neid kasutades võime integreerida ainult üsna ilusaid funktsioone, kõik keerulisem toob juba kaasa probleeme.

Viimaks, kui siiski definitsiooni puudumine teeb tõesti tuska, võib integraali defineerida tuletise ja integraali vahelise seose toel. Nii teeme seda juba tuletise ja integraali peatükis [lk 352].