Ruumiliste kujundite pindalad

Lisaks kahemõõtmelistele kujunditele võib meid muidugi huvitada ka mõne kolmemõõtmelise kujundi välispinna suurus.

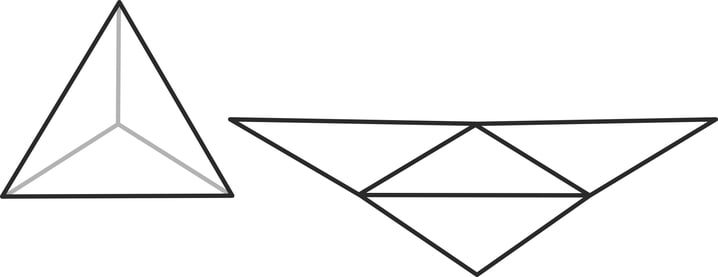
Hulktahukate ehk igasugu erinevate risttahukate ja püramiididega, mille tahud on hulknurksed, käib asi üsna lihtsalt: lõikame kujundi mööda servasid lahti ning arvutame iga tahu pindala eraldi välja. Liites need kõik kokku, saamegi kogu pindala.

Näiteks kolmnurkse põhjaga püramiidi külgpindala leidmiseks peame kokku liitma nelja kolmnurga pindala.

Koonuse pindala

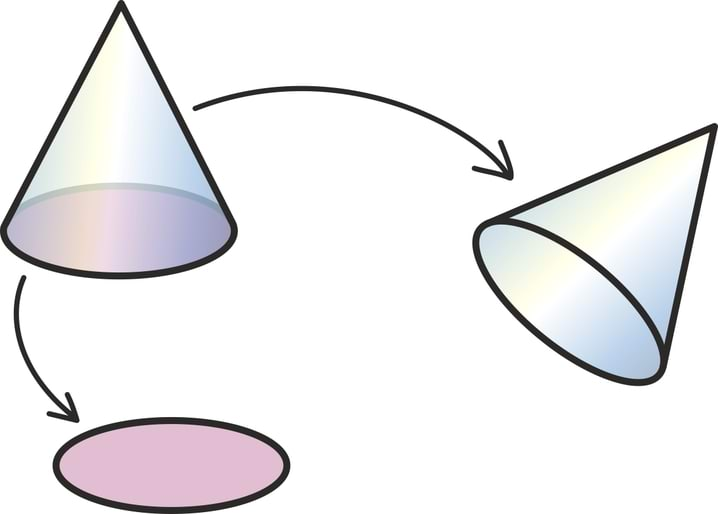
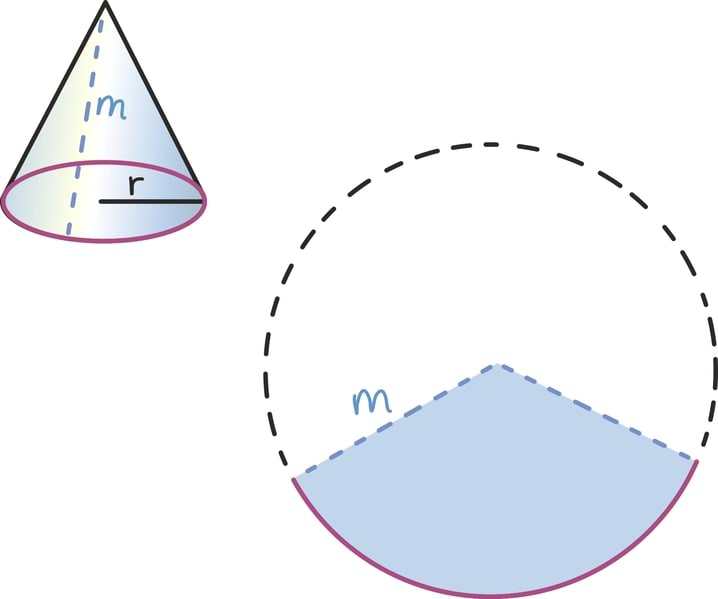
Üldiselt läheb kumeramate kehadega olukord keerulisemaks, aga koonuse korral aitab siiski üsna sarnane strateegia. Alustuseks võime koonuse pinna jagada kaheks – saame ringikujulise põhja ning teatava kujuga külgpinna.

Kuna ringi pindala juba oskame leida, on põhja pindala arvutamine kerge. Aga kuidas leida selle allesjäänud koonuselise tüki pindala?

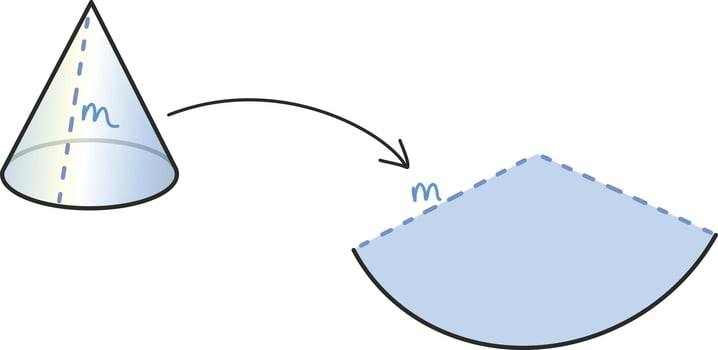
Seegi kord aitab meid veel lõikamine ning tasandile asetamine. Nimelt kui lõikame koonuse külgpinna mööda moodustajat – ehk mööda suvalist koonuse tippu ja põhja äärt ühendavat sirglõiku – lahti ja laotame tasandile, saame ilusa ringi sektori.

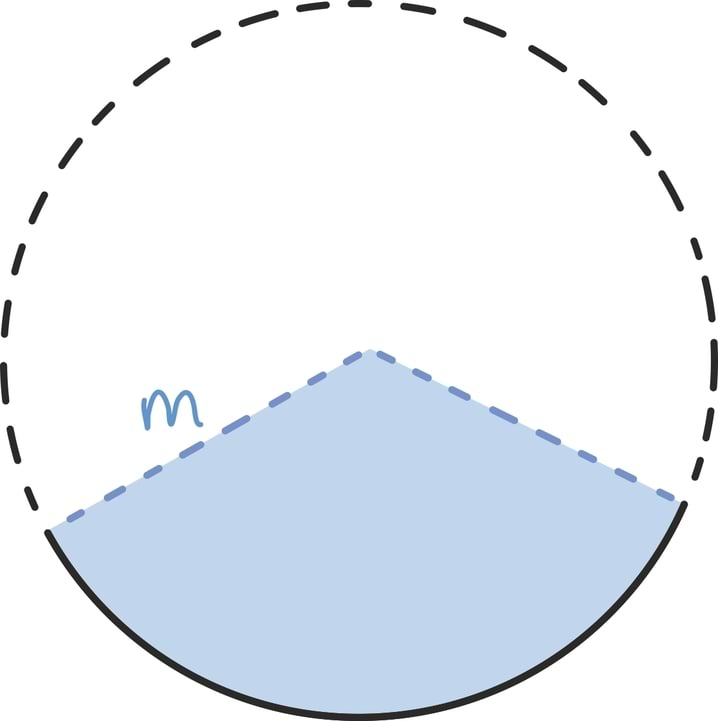
See sektor moodustab teatava osa suurest ringist raadiusega m, kus m on siis niinimetatud koonuse moodustaja. Selle algse ringi pindala oskame jälle lihtsalt leida:

m^{2} π

Seega oleks vaja lihtsalt aru saada, kui suure osa moodustab laiali laotatud sektor kogu ringist. Ringjoone sektori pindala suhe kogu ringi pindalasse on aga täpselt sama kui sektori kaarepikkuse suhe kogu ringjoone ümbermõõtu. Kuna kogu ringi ümbermõõt on meile teada (2mπ), siis piisab lihtsalt sektori kaare pikkusest. Sektori kaare pikkus on aga täpselt koonuse põhja ümbermõõt! Seega, kui põhja raadiuseks on näiteks r, siis saame põhja ümbermõõduks ja ka kaare pikkuseks 2rπ.

Kui jagame saadud tulemused, näeme, et sektori pindala moodustab kogu pindalast

\frac{2 r π}{2 m π} = \frac{r}{m}

Nüüd võime külgpindala leida, korrutades saadud suhte läbi suure ringi pindalaga:

S_{k ¨ u l g} = \frac{r}{m} m^{2} π = r m π

Liites põhja pindala:

S_{p ˜ o h i} = π r^{2}

Võime leida ka koonuse täispindala

S = π r^{2} + π m r

Kera pindala

Kera pindala leidmiseks aga mõnest lõikamisest enam tõesti ei piisa.Võite proovida apelsinikoort mõistlikult laua peale laiali laotada, nii et ükski koht õhus ei oleks – lihtne see ei ole. Tuleb kasutada juba ringi pindalast tuttavat integreerimise strateegiat.

Intuitiivselt tahaksime ka seekord pinna rõngasteks jagada ning seejärel nende rõngaste pindalad osavalt kokku liita.

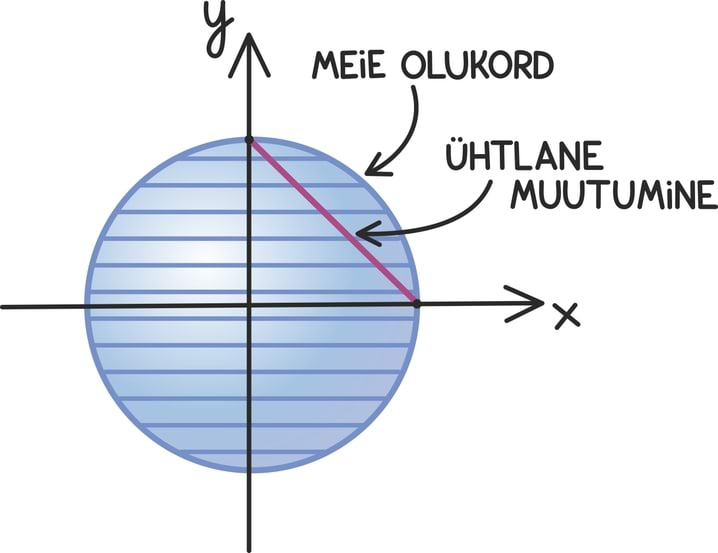
Ringi pindala leidmisest on olukord pisut keerulisem, kuna rõngaste pindalad ise ei muutu enam ilusalt ühtlaselt.

Seega piirdume siinkohal lihtsalt kera pindala valemiga:

P = 4 π r^{2}

Kera ruumala juures anname siiski ka ühe viisi selle pindala leidmiseks.