Vedelikud ja jõud

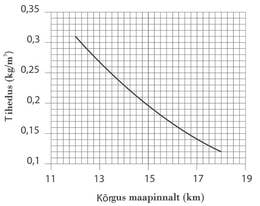
Õhupall, mille ruumala on $V = 2 m^{3}$ , täideti $m = 200 g$ heeliumiga. Õhupalli kesta mass on $M = 180 g$ . Kui kõrgele tõuseb õhupall? Õhu tiheduse sõltuvus kõrgusest maapinnalt $ρ = ρ (h)$ on toodud graafikul ja lihtsuse mõttes loeme palli ruumala konstantseks.

Lahendus

Gaasis (antud juhul õhus) asuvale kehale (õhupallile) mõjub üleslükkejõud. Õhupall tõuseb maapinnast kõrgusele, kus raskusjõud parajasti tasakaalustab üleslükkejõu. Pallile mõjuv raskusjõud avaldub

F_{r} = (m + M) g = (0, 2 k g + 0, 18 k g) \cdot 9, 8 N / k g \approx 3, 72 N

Õhu üleslükkejõud avaldub

F_{¨ u} = ρ_{˜ o hk} V g

. Tingimusest

F_{r} = F_{¨ u}

saame, et õhupall peatub kõrgusel, kus õhu tihedus on võrdne

ρ_{˜ o hk} = \frac{F_{r}}{V g} = \frac{3, 72 N}{2 m^{3} \cdot 9, 8 N / k g} \approx 0, 19 k g / m^{3}

Graafikult saame, et selline on õhu tihedus kõrgusel

15, 1 k m

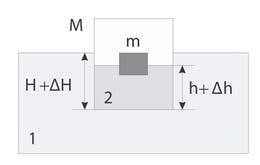
Allveelaeva mass on $m$ ja selle ruumala on $V$ . Allveelaeva mootorid ei tööta ja allveelaev vajub muutumatu kiirusega $v$ . Kui palju tuleb vähendada allveelaeva massi, et allveelaev hakkaks tõusma pinnale sama suure kiirusega $v$ ? Allveelaeva vaadelda silindrina, mille telg on horisontaalne. Vee takistus allveelaevale on võrdeline kiirusega. Vee tihedus on $ρ$ .

Lahendus

Allveelaeva vajumisel kiirusega $v$ kehtib seos

m g = ρ V g + F_{T}

, kus

ρ

on merevee tihedus ja

F_{T}

takistusjõud.

Allveelaeva tõusmisel kiirusega $v$ kehtib seos

ρ V g = (m - m_{1}) g + F_{T}

kus

m_{1}

on väljavisatud koormise mass.

Avaldades mõlemast seosest $F_{T}$ ja võrdsustades tulemused, saame

m g - ρ V g = ρ V g - (m - m_{1}) g

, millest väljavisatud koormise mass

m_{1}

on:

m_{1} = 2 (m - ρ V)

Kangkaalu vasakpoolsele kaalukausile oli asetatud rauast, parempoolsele kaalukausile alumiiniumist keha, kumbki massiga $1 k g$ . Kangkaal sukeldatakse vette, mille tulemusena ei ole kaal enam tasakaalus. Kas kaalu tasakaalustamiseks tuleks lisaraskus asetada vasak- või parempoolsele kaalukausile? Kummast ainest lisaraskus oleks väiksema massiga? Alumiiniumi tihedus on raua tihedusest väiksem.

Lahendus

Kangkaalu tasakaalustmiseks on vaja lisaraskust, sest vees mõjub kehale üleslükkejõud $F_{¨ u} = ρ_{v} g V$ , kus $ρ_{v}$ on vee tihedus. Keha ruumala $V = \frac{m}{ρ}$ . Kaaluvihile mõjub vees jõud

F = m g - F_{¨ u} = m g - \frac{ρ_{v} m g}{ρ} = m g (1 - \frac{ρ_{v}}{ρ})

Kuna

ρ_{A l} < ρ_{F e}

, siis rauast kaaluvihile mõjub suurem jõud, sest

m g (1 - \frac{ρ_{v}}{ρ_{A l}}) < m g (1 - \frac{ρ_{v}}{ρ_{F e}}) \Rightarrow F_{A l} < F_{F e}

Vajalik lisaraskus tuleb asetada alumiiniumist kaaluvihiga samale kaalukausile ehk parempoolsele kaalukausile. Vajalik lisajõud kangkaalu tasakaalustamiseks vees on

F_{l} = F_{F e} - F_{A l} = m_{l} g (1 - \frac{ρ_{v}}{ρ_{l}})

kus indeksiga

l

oleme tähistanud kõik lisaraskuse kohta käivad suurused. Vajaliku lisaraskuse hulk ehk mass ei sõltu jõu

F_{l}

suurusest ehk siis

F_{l} = m_{l} g (1 - \frac{ρ_{v}}{ρ_{l}}) = const.

m_{l}

on minimaalne, kui avaldis sulgudes on suurima võimaliku väärtusega. Arvestades, et

ρ_{v e s i} < ρ_{A l} < ρ_{F e}

, saame

1 - \frac{ρ_{v}}{ρ_{A l}} < 1 - \frac{ρ_{v}}{ρ_{F e}}

Seega raust lisaraskuse mass on väiksem.

Vees ujuva tühja plekktünni ruumalast on $1 / 10$ vee sees. Pärast tünni täitmist tundmatu vedelikuga jääb tünn vee peale ujuma, kuid nüüd on vee sees $9 / 10$ tünni ruumalast. Kui suur on tünni valatud vedeliku tihedus? Vee tihedus on $1000 k g / m^{3}$ .

Lahendus

Tühja tünni korral kehtib seos $m g = \frac{ρ_{v} V g}{10}$ .
Vedelikku täis tünni korral kehtib seos $(m + ρ V) g = \frac{9 ρ_{v} V g}{10}$ .
Taandades ruumala $V$ ja $g$ saame $\frac{ρ_{v}}{10} + ρ = \frac{9 ρ_{v}}{10}$ ,
millest $ρ = \frac{8}{10} ρ_{v}$
Vastus: $ρ = 800 k g / m^{3}$ .

Mari näitas trikki. Ta vajutas küünla vastu silindrilise klaasi põhja ning valas sinna $V_{v} = 150 m l$ vett. Kuigi küünla tihedus $ρ_{k} = 0, 90 g / c m^{3}$ on väiksem kui vee tihedus $ρ_{v} = 1, 0 g / c m^{3}$ , jäi küünal anuma põhja. Juku oli katsest üllatunud. Ta liigutas klaasi ning küünal tõusis pinnale ujuma. "Rikkusid katse!" ütles Mari, "Arvuta nüüd, kui palju muutus rõhk põhjale küünla algses asukohas!". Aita Jukut! Klaasi läbimõõt on $d = 6, 0 c m$ . Küünla ruumala on $V_{k} = 21 c m^{3}$ ja kõrgus $h = 3, 0 c m$ .

Lahendus

1. Arvutame rõhu anuma põhjale küünla all.
Leiame vedelikusamba kõrguse, mille määravad vedeliku ja küünla ruumalad.

V = V_{v e d e l i k} + V_{k ¨ u ¨ u nal} = 150 c m^{3} + 21 c m^{3} = 171 c m^{3}

Põhja pindala:

S = \frac{π d^{2}}{4} = \frac{3, 14 \cdot 6^{2} c m^{2}}{4} = 28, 3 c m^{2}

Veetaseme kõrgus:

h = \frac{V}{S} = \frac{171 c m^{3}}{28, 3 c m^{2}} = 6, 0 c m

Veesamba kõrgus küünla kohal:

h_{v e s i} = h - h_{k ¨ u ¨ u nal} = 6 c m - 3 c m = 3 c m

Rõhk põhjale küünla all ja teisendused ning rõhu väärtus:

p_{1} = ρ_{k ¨ u ¨ u nal} g h_{k ¨ u ¨ u nal} + ρ_{v e s i} g h_{v e s i}

p_{1} = 900 \frac{k g}{m^{3}} \cdot 10 \frac{N}{k g} \cdot 0, 03 m + 1000 \frac{k g}{m^{3}} \cdot 10 \frac{N}{k g} \cdot 0, 03 m = 570 P a

2. Arvutame rõhu põhjale kui küünal ujub $p_{2} = \frac{F}{S} = \frac{m_{v e s i} g + m_{k ¨ u ¨ u nal} g}{S}$ .
Küünla massi saame seosest

ρ = m \Rightarrow m = ρ V = 0, 9 \frac{g}{c m^{3}} \cdot 21 c m^{3} = 19 g

Teisendame ühikud ja arvutame rõhu põhjale

p_{2} = \frac{(0, 15 k g + 0, 019 k g) \cdot 10 \frac{N}{k g}}{28, 3 \cdot 10^{- 4} m^{2}} = 597 P a

3. Arvutame rõhu muutuse $Δ p = p_{2} - p_{1} = 597 P a - 570 P a = 27 P a$ .
Vastus: Kui küünal oli põhjas oli küünla all rõhk põhjale $27 P a$ väiksem kui siis, kui küünal ujus.

Esimene allveelaev "Torpeedo'' (ehitatud 1780 aastal) oli kujult külili asetatud tünn, milles istusid kapten ja tüürimees ning lisaks neile 6 meest, kes ajasid ringi väntvõlli. Kui palju vett on vaja hoida laevas, et laev saaks vee all heljuda? Meeste keskmine mass oli $80 k g$ ning tünni välisläbimõõt $d = 1 m$ ja pikkus $l = 6, 40 m$ ning laeva tühimass $m_{l} = 3000 k g$ .

Lahendus

Allveelaev hulbib veepinnal siis kui tema keskmine tihedus on väiksem vee tihedusest, $ρ_{l a e v} < ρ_{v e s i}$ .On teada, et laeva keskmise tiheduse saab arvutada:

ρ_{l a e v} = \frac{m_{k o g u} + m_{p a a k}}{V_{l a e v}}

kus

m_{k o g u} = 3000 + 8 \cdot 80 = 3640 k g

on laeva kere mass ja inimeste mass kokku,

m_{p a a k}

on vee mass laevas ja

V_{l a e v} = \frac{π d^{2} l}{4} = 5, 02 m^{3}

on laeva ruumala. Lubatud veehulga

V_{p a a k} = \frac{m_{p a a k}}{ρ_{v e s i}}

leidmiseks lähtume eelnimetatud võrratusest, mis annab

V_{p a a k} = \frac{V_{l a e v} - m_{k o g u}}{ρ_{v e s i}} = 1, 38 m^{3}

Õige on ka vastus massiühikutes.

Ühes vedelikus ujub anum massiga $M = 100 g$ (vt. joonis). Anum sisaldab teist vedelikku, mille taseme kõrgus on $h = 15 c m$ . Anuma põhi asetseb $H = 20 c m$ sügavusel. Anumasse pandi ujuma keha massiga $m = 30 g$ . Selle tulemusel vajus anum veel $Δ H = 3 c m$ võrra sügavamale esimesse vedelikku. Kui palju tõusis teise vedeliku tase anumas?

Lahendus

Olgu $S$ anuma aluse pindala, $ρ_{1}$ ja $ρ_{2}$ vastavalt esimese ja teise vedeliku tihedused. Algolekus anuma ning teise vedeliku raskusjõud tasakaalustavad anumale mõjuvat esimese vedeliku ülestõukejõudu: $M g + ρ_{2} S h g = ρ_{1} S H g$ . Keha lisamisel toimub mõlema vedeliku väljatõrjumine massi $m$ poolt . Saame tingimuse $m = ρ_{2} S Δ h = ρ_{1} S Δ H$ . Avaldame siit $ρ_{2} S$ ja $ρ_{1} S$ :

ρ_{2} S = \frac{m}{Δ h}, ρ_{1} S = \frac{m}{Δ H}

ning asendame esimesse võrrandisse:

M g + \frac{m g h}{Δ h} = \frac{m g H}{Δ H} \Rightarrow Δ h = \frac{m h Δ H}{m H - M Δ H} = 4, 5 c m

Alternatiivlahendus:

Anumale mõjuva Archimedese jõu suhteline muutus on võrdne anuma bruto-massi suhtelise muuduga: $\frac{M + m_{v}}{m} = \frac{H}{Δ H}$ , kus $m_{v}$ tähistab vedeliku massi anumas. Rõhu suhteline muutus anuma põhjas on võrdne anuma sisu massi suhtelise muuduga: $\frac{m_{v}}{m} = \frac{h}{Δ h}$ . Asnedades teise võrrandi esimesse leiame

\frac{M}{m} = \frac{H}{Δ H} - \frac{h}{Δ h} \Rightarrow Δ h = \frac{h}{\frac{H}{Δ H} - \frac{h}{Δ h}} = 4, 5 c m

Homogeenne keha riputatakse dünamomeetri külge. Kui keha sukeldatakse vedelikku tihedusega $ρ_{1}$ , on dünamomeetri näit $P_{1}$ , kui aga vedelikku tihedusega $ρ_{2}$ , on dünamomeetri näit $P_{2}$ . Määrake keha tihedus.

Lahendus

Dünamomeetri näit vees on

P_{1} = P - F_{1}

kus

P

on dünamomeetri näit õhus ja

F_{1}

üleslükkejõud vees.

Et $P = m g = ρ V g$ , $F_{1} = ρ_{1} V g$ ja $F_{2} = ρ_{2} V g$ , kus $ρ$ ja $V$ on vastavalt keha tihedus ja ruumala, siis

P_{1} = ρ V g - ρ_{1} V g = (ρ - ρ_{1}) \cdot V g

P_{2} = ρ V g - ρ_{2} V g = (ρ - ρ_{2}) \cdot V g

Avaldame mõlemast valemist ruumala:

V = \frac{P_{1}}{(ρ - ρ_{1}) \cdot g}, V = \frac{P_{2}}{(ρ - ρ_{2}) \cdot g} \Rightarrow ρ = \frac{ρ_{1} P_{2} - ρ_{2} P_{1}}{P_{2} - P_{1}}

Silindrilises anumas on vesi; vee horisontaallõike pindala $S = 200 c m^{2}$ . Anumasse visatakse jäätükke, millesse on külmunud teatud hulk liiva. Alguses ükski jäätükk põhja ei vaju ning vee pind kerkib $h_{1} = 10 c m$ võrra. Tasapisi sulab ära kogu jää, liiv vajub põhja ning veepind langeb vahepealse (kõrgeima) taseme suhtes $h_{2} = 0, 5 c m$ võrra allapoole. Kui suur oli vette visatud jää ja liiva mass? Liivaterade materjali tihedus $ρ_{l} = 2500 k g / m^{3}$ ja vee tihedus $ρ_{v} = 1000 k g / m^{3}$ .

Lahendus

Liiva ja jää kogumass on leitav välja tõrjutud vee massina

m_{t o t} = ρ_{v} S h_{1} = 2 k g

kus

ρ_{v}

on vee tihedus.

Kui liiv sadeneb põhja, siis mõjutab mannergu põhi liivateri jõuga

V_{l} (ρ_{l} - ρ_{v}) g

kus

V_{l}

on liivaterade koguruumala.

Kui jaotada leitud jõud üle mannergu põhja, saame sellele vastava keskmise rõhu

p_{l} = V_{l} (ρ_{l} - ρ_{v}) g / S

mis peab olema võrdne veetaseme langusest tingitud rõhu muutusega (süsteemi ``vesi+liiv'' kaal ju ei muutu). Seega

V_{l} (ρ_{l} - ρ_{v}) g / S = ρ_{v} g h_{2}

ning järelikult

m_{l} = V_{l} ρ_{l} = \frac{ρ_{l} ρ_{v} h_{2} S}{ρ_{l} - ρ_{v}} \approx 170 g

Jää mass oli niisiis $m_{j} = m_{t o t} - m_{l} \approx 1830 g$ .

Keset merd jääpangal triiviv jääkaru (massiga $M = 700 k g$ ) tapab käpalöögiga tema lähedal meres ujunud hülge (mass $m = 70 k g$ ). Hüljest söömiseks pangale tirides avastab jääkaru, et jääpank kipub hülge peale vinnamisel viimasel hetkel vee alla vajuma. Teades, et enne hülgepüüki oli $99 %$ jääpangast vee all, hinnake jää tihedust. Vee tihedus olgu $ρ_{v} = 1 g / c m^{3}$ .

Lahendus

Olgu panga ruumala $V$ ja jää tihedus $ρ_{j}$ . Raskusjõu ja üleslükkejõu tasakaalust (ujumise tingimusest) saame

0, 99 ρ_{v} V = V ρ_{j} + M

Hülge massi lisamisel vajub kogu pank vee alla. Siit saame tingimuse:

V ρ_{v} = V ρ_{j} + M + m

Lahendades võrrandid

ρ_{j}

suhtes, saame

ρ_{j} = ρ_{v} (0, 99 - (1 - 0, 99) \frac{M}{m}) \approx 0, 9 g / c m^{3}

Ühele kaalukausile on asetatud veega ääreni täidetud pang. Teisele kaalukausile asetatakse samasugune ääreni veega täidetud pang, milles ujub puutükk. Millise asendi võtavad kaalud? Põhjenda vastust.

Lahendus

Kaalud on tasakaalus. Kuna puutükk ujub, siis tõrjub see enda alt välja vee koguse, mille mass võrdub puutüki massiga. Kui pang oli enne katset vett täis, siis puutüki asetamisel pange voolas väljatõrjutud vesi üle panga serva maha koguses, mille mass on võrdne puutüki massiga, järelikult pange mass ei ole muutunud.

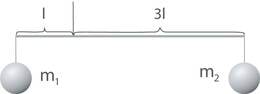
Kraana trossi külge on kinnitatud kang, mille kummaski otsas on sama ruumalaga koormis (vt. joonis). Kang on tasakaalus. Kraana laseb koormised vette nii, et kang ise vette ei lähe. Selle tulemusel kangi tasakaal kaob. Kangi ülestõusnud otsale ronib töömees ja kang läheb uuesti tasakaalu. Leidke koormiste ruumala. Töömehe mass on $80 k g$ ja vee tihedus on $1000 k g / m^{3}$ . Kas kangi massi arvestamine mõjutab vastust?

Lahendus

Õhus kehtib seos: $m_{1} g l = m g l + m_{2} g \cdot 3 l$ , millest $m_{1} = m + 3 m_{2}$ .

Vees mõjub koormistele üleslükkejõud. Kangi vasakule pöörav jõumoment on: $(m_{1} g - ρ_{v} g V) l$ .

Kangi paremale pöörav jõumoment on: $m g l + (m_{2} g - ρ_{v} g V) \cdot 3 l$ Asendades $m_{1}$ seosega $m_{1} = m + 3 m_{2}$ ja võrreldes jõumomente selgub, et koormiste vette sukeldamise korral tõuseb üles kangi parempoolne ots.

Seega kang on vettesukeldatud koormiste korral tasakaalus siis, kui paremale otsale ronib mees massiga $Δ m$ . Pärast teisendust saame

V = \frac{3 Δ m}{2 ρ_{v}} = 0, 12 m^{3}

Kangkaalu kaussidele asetatakse kaks ühesugust klaasi. Üks klaasidest on ääreni täidetud veega, teine samuti, kui selles ujub puitklots. Kas kaal jääb tasakaalu?

Lahendus

Jääb küll, sest klotsi ujumise korral klotsi poolt anumast välja tõrjutud vee mass võrdub klotsi massiga.

Vett täis anumas asub vetikaalselt õhukeste seintega toru, mille sisemine läbimõõt on $d = 2 c m$ . Toru alumine ots on $70 c m$ sügavusel vees ja selle vastu on surutud tihedalt õhukene ruudukujuline plaat küljepikkusega $a = 3 c m$ . Plaadi pindtihedus (massi ja pindala suhe) $δ = 4, 5 k g / m^{2}$ . Torusse valatakse õli tihedusega $ρ = 900 k g / m^{3}$ . Kui kõrge õlisamba võib torusse valada, enne kui plaat eraldub toru otsast? Plaadi ja toru paksust ei ole vaja arvestada. Vee tihedus $ρ = 1000 k g / m^{3}$ .

Lahendus

Plaadile mõjub alt üles vee rõhumisjõud, ülevalt alla vee rõhumisjõud ja õlisamba rõhumisjõud. Kuna väljaspool toru mõjuvad vee rõhumisjõud kompenseerivad üksteist, arvestame arvutustes ainult seda plaadi osa, mis on vahetult toru otsa all. Alt üles mõjub jõud

F_{¨ u les} = p S = ρ_{v e s i} g h_{v e s i} \frac{π d^{2}}{4}

ülevalt alla mõjub plaadile raskusjõud

F_{a l l a} = m g = δ \frac{π d^{2}}{4} g

ja õlisamba rõhumisjõud

F_{a l l a} = ρ_{˜ o li} g h ˜ o li \frac{π d^{2}}{4}

õlisammas on kõrgeim siis, kui alt üles ja ülevalt alla mõjuvad jõud on võrdsed

δ S g + ρ_{˜ o li} g h_{˜ o li} S = ρ_{v e s i} g h_{v e s i} S

millest

h_{˜ o li} = \frac{ρ_{v e s i} h_{v e s i} - δ}{ρ_{˜ o li}} = 77, 3 c m

Võrdkülgse kolmnurga $A B C$ tippudes $A$ , $B$ ja $C$ asuvad võrdse ruumalaga kerad tihedustega vastavalt $0, 5$ , $1$ ja $1, 2 g / c m^{3}$ , mis on omavahel ühendatud kaalutute jäikade varrastega. Missuguse nurga moodustab külg $A B$ veepinnaga, kui konstruktsioon visata sügavasse veevanni?

Lahendus

Kolmnurga keskmine tihedus on väiksem kui $1 g$ milliliitri kohta ja seega konstruktsioon tervikuna asub veepinnal. Tipus $B$ asuvale kerale mõjuv resultantjõud on 0 (sest ta tihedus on võrdne vee tihedusega) ja seega võib seda kera vaadelda kui kangi pöörlemiskeskpunkti.

Kehale $C$ mõjuv resultantjõud on võrdne ja vastassuunaline kerale $A$ mõjuva resultantjõuga.

Uurides nüüd kolmnurga pöörlemist ümber tipu $B$ on näha, et jõud kerale $A$ ja kerale $C$ mõjuvad mooda ühte ja sama sirget, kui külg $A C$ on risti veepinnaga. See vastab tasakaalulisele olukorrale, sest nihkel sellest asendist hakkab üks kera pöörlemispunktile lähenema ja teine kaugenema ja pöördemomendid pole sellel juhul enam võrdsed.

Lihtsast geomeetriast on näha, et külje $A B$ nurk veepinnaga on tasakaaluasendis $30$ kraadi.

Kraanaga tõsteti laevalt kaile tühja risttahukakujulist kaubakonteinerit, mille kesta (seinamaterjali) ruumala on $V_{k}$ . Kraana tross katkes ja konteiner kukkus vette. Vahetult pärast vettekukkumist oli konteineri vee all oleva osa ruumala $V_{1}$ . Kuna konteiner polnud täielikult hermeetiline, pääses õhk konteinerist välja ja vesi voolas sisse. Kui konteineri ülemine tahk oli vajunud veekogu tasapinnani, oli konteineri ülemisse ossa moodustunud õhupadi. Avaldage selle õhupadja ruumala $V\widetilde{o}$ .

Lahendus

Olgu konteineri materjali tihedus $ρ_{k}$ ja vee tihedus $ρ$ . Vahetult vette kukkumise järel mõjus konteinerile üleslükkejõud $F\ddot{u}=ρV1g$ ja raskusjõud $F_{g} = m g = ρ_{k} V_{k} g$ . Kuna konteiner ujus, siis $ρ V_{1} g = ρ_{k} V_{k} g$ .

Olgu äsja vee alla vajunud konteineris õhupadja ruumala $V\widetilde{o}$ . Konteineri sisemuse ruumala oli $V_{s} = V - V_{k}$ ja konteineris oleva vee ruumala oli $Vv=V−Vk−V\widetilde{o}$ . Konteinerile mõjub raskusjõud $F_{g 1} = ρ_{k} V_{k} g$ ja konteineris olevale veele mõjub raskujõud $Fg2=Vvρg=(V−Vk−V\widetilde{o})ρg$ . Konteinerile ja selles olevale veele mõjub summaarne üleslükkejõud $F\ddot{u}2=Vρg$ .

Kuna keha heljub, siis konteineri ja selles oleva vee raskusjõudude summa võrdub üleslükkejõuga.

F_{g 1} + F_{g 2} = F_{¨ u 2} \Rightarrow ρ_{k} V_{k} g + (V - V_{k} - V_{˜ o}) ρ g = V ρ g

Asendame sellesse valemisse konteineri raskusjõu:

ρ V_{1} g + (V - V_{k} - V_{˜ o}) ρ g = V ρ g

Avame sulud, taandame ja koondame:

ρ V_{1} g + V ρ g - V_{k} ρ g - V_{˜ o} ρ g = V ρ g \Rightarrow V_{1} + V - V_{k} - V_{˜ o} = V \Rightarrow V_{˜ o} = V_{1} - V_{k}

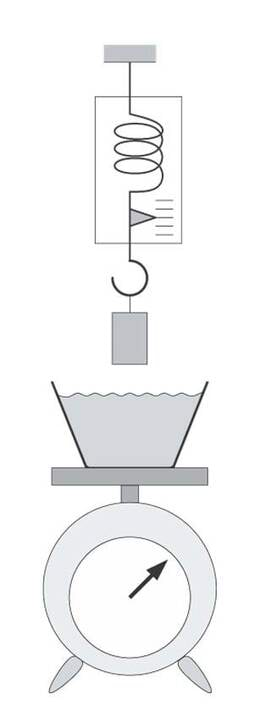
Kaalu peal on anum veega. Selle kohal on vedrukaal, mille külge on riputatud koormis massiga $m$ . Kaaalude näidud on võrdsed. Kui palju erinevad kaalude näidud, kui koormis lastakse üleni vette? Koormis ei puutu anuma põhja. Vee tihedus on $ρ_{V}$ ja koormise tihedus on $ρ_{K}$ .

Lahendus

Olgu kaalude näidud algselt $F$ . Kui koormis lasti vette, hakkas koormisele mõjuma üleslükkejõud $F_{y}$ . Seega koormise kaal vähenes.

Sama palju aga anuma kaal suurenes. Koormise kaal on nüüd $F_{1} = F - F_{y}$ ja anuma kaal on $F_{2} = F + F_{y}$ .

Kaalude näidud erinevad $Δ F = F_{2} - F_{1} = 2 F$ võrra. Koormisele mõjuv üleslükkejõud on $F = ρ V g$ , kus koormise ruumala

V = \frac{m}{ρ_{K}}

. Seega

Δ F = 2 ρ V g = 2 m g \frac{ρ_{V}}{ρ_{K}}

Korgitükk massiga $1, 2 g$ on seotud tüki raua külge, mille mass on $4, 4 g$ . Kui panna need seotud kehad vette, siis nad heljuvad seal (ei tõuse pinnale ega vaju põhja). Millega võrdub korgi tihedus, kui raua tihedus on $7, 8 g / c m^{3}$ ?

Lahendus

Heljuvate kehade keskmine tihedus on võrdne vee tihedusega. Kui korgi tihedus ja mass on vastavalt $ρ_{k}$ ja $m_{k}$ , rauatüki tihedus ja mass - $ρ_{r}$ ja $m_{r}$ , vee tihedus - $ρ_{v}$ , siis

\frac{m_{k} + m_{r}}{V_{k} + V_{r}} = ρ_{v}

kus

V_{k}

V_{r}

on korgitüki ja rauatüki ruumalad. Võrdusest leiame kasutades asendust

V = m / ρ

ρ_{k} = \frac{ρ_{v} m_{k}}{m_{k} + m_{r} + ρ_{v} m_{r} / ρ_{r}} =\approx 0, 24 g / c m^{3}

Pikkusega $d_{1} = 49, 4 c m$ peenikese varda keskpunkt on kinnitatud vertikaalselt rippuva niidi otsa nii, et tasakaaluasendis on varras horisontaalne. Varda otsa kinnitatakse hapnikuga täidetud õhupall. Millisel kaugusel selle õhupalli kinnituspunktist tuleb kinnitada teine sama ruumalaga, kuid heeliumiga täidetud õhupall, et varras jääks horisontaalasendisse? Hapniku ja heeliumi tihedused on vastavalt $ρ_{1} = 1, 54 k g / m^{3}$ ja $ρ_{2} = 0, 19 k g / m^{3}$ , õhu tihedus $ρ_{0} = 1, 16 k g / m^{3}$ . Õhupallide materjali massi lugeda tühiseks.

Lahendus

Mõlemale õhupallile mõjub raskusjõud ja üleslükkejõud. Hapnikuga täidetud pallile mõjub summaarne jõud

F_{1} = m_{1} g - ρ_{0} g V = (ρ_{1} - ρ_{0}) g V

mis on suunatud allapoole. Heeliumiga täidetud pallile mõjub aga jõud

F_{2} = ρ_{0} g V - m_{2} g = (ρ_{0} - ρ_{2}) g V

mis on suunatud ülespoole. Järelikult tasakaalu hoidmiseks tuleb hapnikuga ja heeliumiga pall kinnitada samale poole niidi kinnituspunktist vardaga. Olgu hapnikuga täidetud palli kinnituspunkti kaugus niidi kinnituspunktist

d_{2}

. Kirjutame välja kangi reegli:

F_{1} l_{1} = F_{2} l_{2}

kus

l_{1} = \frac{d_{1}}{2}

l_{2} = d_{2}

on jõuõlad (niidi kinnituspunkti suhtes). Asendades jõu väärtused, saame

\frac{(ρ_{1} - ρ_{0}) g V d_{1}}{2} = (ρ_{0} - ρ_{2}) g V d_{2}

\frac{(ρ_{1} - ρ_{0}) d_{1}}{2} = (ρ_{0} - ρ_{2}) d_{2}

Nüüd saame avaldada

d_{2}

d_{2} = \frac{ρ_{1} - ρ_{0}}{ρ_{0} - ρ_{2}} \cdot \frac{d_{1}}{2} = 9, 7 c m

Järelikult tuleb heeliumiga täidetud õhupall kinnitada

\frac{d_{1}}{2} - d_{2} = 15, 0 c m

kaugusele hapnikuga täidetud õhupallist.

Part laskus veetünni. Selle tulemusel tõusis veepind $12 m m$ võrra. Seejärel sukeldus ta tünni põhjas siputava ussikese järele. Nüüd tõusis veepind veel $10 m m$ võrra. Vaba vee pindala tünnis oli $0, 80 m^{2}$ . Kui suur on pardi tihedus ja mass?

Lahendus

Pardi laskumisel vette osa pardist jääb vee alla, kusjuures Archimedese seaduse järgi on pardi poolt välja tõrjutud vee mass võrdne pardi massiga, seega on pardi mass $m = ρ S d_{1}$ ,

M = 1000 \frac{k g}{m^{3}} \cdot 0, 8 m^{2} \cdot 0, 012 m = 0, 96 k g

Pardi sukeldumisel tõrjub ta välja vett vastavalt oma ruumalale, järelikult on pardi ruumala

V = S \cdot (d_{1} + d_{2})

. Seega on pardi tihedus

ρ_{P} = \frac{m}{V} = \frac{0, 96 k g}{0, 8 m^{2} \cdot 0, 022 m} \approx 550 k g / m^{3}

Rõhutame, et see on pardi tihedus koos sulgedevahelise õhuga.

Milline peab olema $d = 40 c m$ paksuse puitparve pindala, et ta suudaks vee peal hoida koormust, mille kaal on $P = 400 N$ ? Parv võib vette vajuda $h = 38 c m$ sügavusele. Puidu tihedus on $ρ_{p} = 0, 9 g / c m^{3}$ , vee tihedus on $ρ_{v} = 1 g / c m^{3}$ .

Lahendus

Arvutame kui sügavale vajub tühi parv. Olgu parve vee all asuv osa $d_{1}$ ja parve ristlõikepindala $S$ . Siis peab kehtima võrdus: $ρ_{p} d S = ρ_{v} d_{1} S$ , mis tähendab, et parve poolt välja tõrjutud vee mass on võrdne parve massiga. Sellest võrdusest saame, et $d_{1} = ρ_{p} d / ρ_{v} = 0, 9 \cdot 40 / 1 = 36 c m$ . Kuna on öeldud, et parv saab vajuda vee alla vaid $h = 38 c m$ võrra, siis tähendab see, et parve peal asuv koormus võib parve vee alla suruda vaid $h - d_{1} = 2 c m$ võrra. Järelikult võib panna kirja teise võrduse

\frac{P}{g} = ρ_{v} S (h - d_{1}) \Rightarrow S = \frac{P}{ρ_{v} g (h - d_{1})} = 2 m^{2}

Õhukesest plekist valmistatakse kaks kaaneta kuupi (st üks tahk on kummalgi puudu), kusjuures nende mahud erinevad 8 korda. Kuubid ujuvad vees ja mõlemasse hakatakse aeglaselt vett lisama. Üks kuup läheb põhja, kui $90 %$ tema ruumalast on veel veest tühi. Mitu protsenti teisest kuubist on tühi tema uppuma hakkamise hetkel?

Lahendus

Olgu selle kuubi, mis upub, kui temast $α = 90 %$ on tühi, seinte mass $m$ ja ruumala $V$ . Archimedese seaduse põhjal hakkab objekt uppuma, kui ta tihedus saab suuremaks vee tihedusest $ρ_{v}$ (piirjuhul võrdseks):

\frac{m + ρ_{v} (1 - α) V}{V} = ρ_{v} \Rightarrow \frac{m}{V} = α ρ_{v} (*)

Teine kuup võiks olla nii väiksem kui suurem. Oletame algul, et ta on väiksem. Siis on selle kuubi ruumala

\frac{1}{8} V

. Kuubi seinte mass on võrdeline nende pindalaga, mis on omakorda võrdeline küljepikkuse ruuduga. Et teise kuubi küljepikkus on esimese omast

\sqrt[3]{8} = 2

korda väiksem, on ta pindala

2^{2} = 4

korda väiksem ning seinte mass seega

\frac{1}{4} m

. Kirjutame analoogiliselt uppumahakkamise tingimuse, kus

β

tähistagu otsitavat õhu osa teises kuubis.

\frac{\frac{1}{4} m + ρ_{v} (1 - β) \frac{1}{8} V}{\frac{1}{8} V} = ρ_{v} \Rightarrow \frac{2 m}{V} = β ρ_{v}

Võrrandist

(*)

ρ_{v} = \frac{m}{α V}

, seega

β = 2 α = 180 % > 100 %

, mis on võimatu. Järelikult upuks teine kuup väiksemana juba ilma vett lisamatagi, vastuolus öelduga, et kuubid ujuvad.

Oletame nüüd, et teine kuup on suurem, ruumalaga $8 V$ ja massiga $4 m$ . Uppumahakkamise tingimus on siis

\frac{4 m + ρ_{v} (1 - β) 8 V}{8 V} = ρ_{v} \Rightarrow \frac{m}{2 V} = β ρ_{v}

Siit

β = \frac{1}{2} α = 45 %

, mis jääbki ainsaks, üheseks vastuseks.

Praami pikkus on $15 m$ ja laius $4 m$ . Kui sügavale vajub praam, kui sellele sõidab $3$ tonni raskune auto? Praam on risttahuka kujuline.

Lahendus

Vastavalt Archimedese seadusele auto poolt välja tõrjutud vee mass peab võrduma auto massiga. Järelikult välja tõrjutud vee mass on $3000 k g$ . Selle vee ruumala on

Δ V = M / ρ = \frac{3000 k g}{1000 k g / m^{3}} = 3 m^{3} .

Praami ristlõikepindala on

S = 15 m \cdot 4 m = 60 m^{2}

. Järelikult vajub praam

Δ h = \frac{Δ V}{S} = \frac{3 m^{3}}{60 m^{2}} = 0, 05 m = 5 c m

võrra sügavamale.

On võimalik ka teine, veidi erinev, lahenduskäik. Tühja praami kaalu $P$ tasakaalustab Archimedese jõud $F_{A 1} = ρ g L d h = P$ , kus $ρ = 1000 k g / m^{3}$ on vee tihedus, $L = 15 m$ ja $d = 4 m$ on praami mõõtmed, ning $h$ on praami veealuse osa esialgne kõrgus. Praami koos autoga tasakaalustab Archimedese jõud

F_{A 2} = ρ g L d \cdot (h + Δ h) = P + M g,

kus

M

on auto mass. Lahutades teisest võrrandist esimese, saame

ρ g L d Δ h = M g

, kust

Δ h = \frac{M}{ρ L d} = \frac{3000}{1000 \cdot 15 \cdot 4} = 0, 05 m

Seest tühi teraskera ujub veepinnal nii, et täpselt pool sellest on vees. Kui suure osa kera ruumalast moodustab kera sees oleva õõnsuse ruumala? Terase tihedus on $7800 k g / m^{3}$ ja vee tihedus $1000 k g / m^{3}$ . Kera õõnsuses oleva õhu massi võib arvutustes jätta arvestamata.

Lahendus

See, et täpselt pool ujuvast teraskerast on vees, tähendab, et teraskera tihedus on täpselt kaks korda vee tihedusest väiksem ehk $ρ_{k} = ρ_{v} / 2$ .

Tähistades kera massi $m$ , kera ruumala $V_{k}$ ning terase ruumala $V_{t}$ , saame panna kirja kaks seost: ühelt poolt $m = ρ_{k} V_{k}$ , teisest küljest $m = ρ_{t} V_{t}$ , kust avaldame $V_{t} / V_{k} = ρ / ρ_{t} = ρ_{v} / 2 ρ_{t} \approx 0, 06 = 6 %$ .

Järelikult moodustab õõnsus $94 %$ teraskera ruumalast.

Anumas olevas vees tihedusega $ρ_{v} = 1, 0 k g / d m^{3}$ ujub kuubikujuline ujuk, mille alumine pool on jääst tihedusega $ρ_{j} = 0, 9 k g / d m^{3}$ ja ülemine pool vahtplastist tihedusega $ρ_{p} = 0, 3 k g / d m^{3}$ . Kuubi serva pikkus $a = 4 c m$ . Ujuki jääst osa sulab. Kui palju muutub ujuki ülemise tahu kaugus veepinnast?

Lahendus

Ujuki kummagi osa ruumala $V = 32 c m^{3}$ . Ujuki jäätüki mass $m_{j} = V \cdot 0, 9 ρ_{v}$ ja ujuki vahtplasti mass $m_{p} = V \cdot 0, 3 ρ_{v}$ . Ujuki kogumass $m_{j} + m_{p} = 1, 2 V ρ_{v}$ .

Teame, et

m g = ρ_{v} g V_{v}

millest ujuki veealuse osa ruumala

V_{v} = V \cdot \frac{1, 2 ρ_{v}}{ρ_{v}} = 38, 4 c m^{3}

Vees oleva osa kõrgus $h = 2, 4 c m$ ja veepealse osa kõrgus $1, 6 c m$ . Pärast jää sulamist on ujuki veealuse osa ruumala on

V_{v 1} = V \cdot \frac{0, 3 ρ_{v}}{ρ_{v}} = 9, 6 c m^{3}

Nüüd on vees oleva osa kõrgus

h_{1} = 0, 6 c m

ja veepealse osa kõrgus

1, 4 c m

Seega ujuk vajub allapoole võrreldes esisalgse olukorraga $h - h_{1} = 0, 2 c m$

Millise oma keha suhtes mahult väikseima puitklotsi peaksite võtma, et hoides sellest kinni võiksite hoida ennast veepinnal nii, et pea ja õlad (1/8 teie ruumalast) oleks veest väljas? Puidu tihedus on $0, 6 g / c m^{3}$ , inimese tiheduseks võtke $1, 075 g / c m^{3}$ .

Lahendus

Olgu $V_{1}$ - klotsi ruumala, $V_{2}$ - inimese ruumala, $ρ_{1}$ - puidu tihedus, $ρ_{2}$ - inimese tihedus, $ρ$ - vee tihedus, $g$ - raskuskiirendus.

(ρ_{1} V_{1} + ρ_{2} V_{2}) g = ρ g (V_{1} + (7 / 8) V_{2}) \Rightarrow 0, 4 V_{1} = 0, 2 V_{2} \Rightarrow V_{1} = 0, 5 V_{2}

ehk klotsi ruumala peaks olema pool inimese ruumalast.

Risttahukakujulisse anumasse põhja pindalaga $S_{1}$ asetatakse ujuma väiksem risttahukakujuline anum põhjapindalaga $S_{2}$ . Selle tulemusel tõusis veetase suures anumas kõrguse $Δ h$ võrra. Siis hakati väiksemasse anumasse vett valama. Milline on minimaalne kaugus väiksemas anumas oleva vee pinna ja väikese anuma ääre vahel nii, et see veel ei upuks?

Lahendus

Anuma jaoks ilma veeta: $m g = ρ g V$ , kus $m$ on anuma mass, $ρ$ on vee tihedus ja $V$ on anuma vee alla jääva osa ruumala. Kuna vesi on kokkusurumatu, siis selle sama ruumala võrra surutakse vett ka välja:

V = Δ h (S_{1} - S_{2})

Avaldame anuma massi:

m = ρ Δ h (S_{1} - S_{2})

. Väiksem anum upub, kui ta vajub piisavalt sügavale, et vesi saaks hakata sisse voolama. Tasakaalutingimuse saab kirja panna nii:

m g + ρ V_{s} g = ρ V g

, kus

V_{s}

on anumas oleva vee ruumala ja

V

on kogu anuma ruumala. Piirjuhul on meil

V_{s} = S_{2} h

V = S_{2} H

, kus

h

on veetaseme kõrgus anumas ja

H

on anuma kõgus. otsitav minimaalne kaugus avaldub:

Δ l = H - h

. Eelnevat arvesse võttes saame:

ρ (V - V_{s}) = m

H - h = \frac{m}{ρ S_{2}}

Δ l = \frac{(S 1 - S 2)}{S_{2}} Δ h

Vees ujub vahtrapuust kuup servapikkusega $a = 10 c m$ tihedusega $ρ_{v a h e r} = 700 k g / m^{3}$ . Kuubi sees on silindriline õõnsus läbimõõduga $b = 4, 5 c m$ (vt joonist). Õõnsus on alt suletud õhukese korgiga. $a)$ Arvutage, kas kuup upub, kui õõnsus täita liivaga? Liiva tihedus on $ρ_{l i i v} = 2700 k g / m^{3}$ ja vee tihedus on $ρ_{v e s i} = 1000 k g / m^{3}$ . $b)$ Kui korgile mõjuv summaarne jõud on suurem kui $1, 8 N$ , läheb kork katki. Mis on maksimaalne liiva kõrgus, mida saab õõnsusesse valada?

Lahendus

$a)$ Leiame maksimaalse raskusjõu ja üleslükkejõu ning vaatame kas üleslükkejõud on väiksem kui raskusjõud.

F_{r} = F_{k l o t s} + F_{l i i v} = (ρ_{v a h e r} (a^{3} - \frac{π b^{2} a}{4}) + \frac{ρ_{l i i v} π b^{2} a}{4}) g = 9, 975 N

F_{y} = ρ_{v e s i} g a^{3} = 9, 8 N

Seega klots on võimalik ära uputada.

$b)$ Korgile mõjub liiva raskusjõud ning altpoolt surub seda vesi. Kork kannatab nende jõudude vahet.

1, 8 N = ρ_{l i i v} S h g - ρ_{v e s i} g A S

kus

S = π b^{2} / 4

- augu põhja pindala,

h

- liivasamba kõrgus,

A

- klotsi vee alla ulatuva osa kõrgus. Teise seose saame panna kirja klotsi ujumise tingimustest

F_{r} = F_{y}

(ρ_{v a h e r} (a^{3} - S a) + ρ_{l i i v} S h) g = ρ_{v e s i} g a^{2} A

Lahendades need võrrandid, saame, et

A = 0, 092 m = 9, 2 c m

ning

h = 0, 0768 m = 7, 68 c m

. Ehk kork eemaldub enne kuubiku uppumist ja seega ei saa kuubikut sellel viisil uputada.

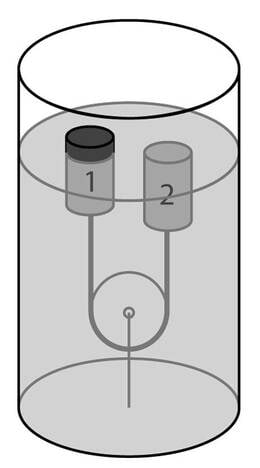
Silindrilises anumas põhjapindalaga $S$ on vesi tihedusega $ρ$ . Anuma põhjas on plokk ja üle hõõrdevabalt pöörleva plokiratta on tõmmatud nöör. Nööri otste külge on kinnitatud kaks veest väiksema tihedusega keha. Plokk takistab nende kehade veepinnale kerkimist (vt joonis). Kummagi keha ruumala on $V$ . ühe keha tihedus on $ρ_{1}$ ja teise keha tihedus $ρ_{2}$ , kusjuures $ρ_{1} < ρ_{2} < ρ$ . Plokinöör on nii pikk, et kumbki kehadest ei puuduta plokki ning nii lühike, et üks keha on tõmmatud üleni vee alla. Kui palju muutub anumas oleva vee tase kui plokinöör katkeb ja mõlemad kehad kerkivad vee pinnale?

Lahendus

Arvutame anuma põhja poolt süsteemile ``vesi pluss kehad'' mõjuva jõu muutuse: \vspace{-5pt}

Δ F = - 2 T = S ρ g Δ h,

\vspace{-25pt} kus

T

on nööri pinge. Tõepoolest, nimetatud jõud tasakaalustab kõikide ülejäänud jõudude resultandi, milleks on raskusjõudude summa (ei muutu) pluss nööri poolt mõjuv jõud. Et nööri pinge hoiab teist keha vee all, siis

T = (ρ - ρ_{2}) g V

, millest

Δ h = - \frac{2 (ρ - ρ_{2}) V}{S ρ} .

1. Õhupall

2. Allveelaev

3. Weight

4. Tünn

5. Küünal purgis

6. Allveelaev

7. Anum vees

8. Homogeenne keha

9. Jää ja liiv

10. Jääkaru

11. Scales

12. Lever

13. Fabric weight

14. Klapp

15. Kolmnurk

16. Konteiner

17. Koormis vees

18. Korgitükk

19. Õhupallid

20. Part

21. Parv

22. Plekkkuubid

23. Praam

24. Teraskera

25. Ujuk

26. Ujumine

27. Ujuv anum

28. Uppuv klots

29. Äpardus plokiga