We are talking about periodic movements, that is, movements that repeat themselves over a certain period of time. For example, the same pendulum.
Before starting to act, yellow boxes with important sentences, such as you often come across in textbooks, would show. Here you don't have to memorize them. But if we want to talk about something matter-of-factly, the first thing we should do is agree on what these words mean, what we use. Eksole, we usually feel pretty confident talking about cars, for example. Because we've seen cars and know what we generally mean by that word. And, by the way, even though we haven't learned the definition of the word "car" anywhere, we could probably come up with one ourselves. It should be the same with the concepts of physics - if you know what it is, you can come up with the definition yourself.
Here you will also find a simple formula - how the frequency of periodic oscillation is expressed according to its oscillation period. Also, two review questions that you might want to answer.
So:
In other words, what does and does not depend on the period of oscillation of a pendulum?
Let's try it.
If we want to study something like this, we should do several experiments where we change one or another property of the pendulum, after which we also measure the period of oscillation. And then draw conclusions. When doing this first mini-research, we don't measure, we compare - we put another one next to the already existing pendulum. And let's try to answer the questions on the next slide.
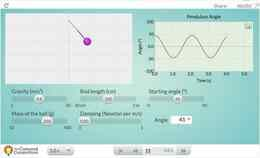
The period of oscillation and the frequency of oscillation of the pendulum depend on which parameters
I do these tests like this:
VIDEO
Now for the ugly slide where we do math. Although some of you may not like math, it can be really useful from time to time. And physics cannot do without mathematics.
Let's get acquainted with mathematics through the pendulum formula. The formula also has a pendulum defined for which this formula is valid.
One property of the pendulum goes into the formula - its length. The period of oscillation of the pendulum can be calculated through the formula. The measured and calculated oscillation period should be the same?
Why do we need mathematics
We have now dealt with the period of oscillation of the pendulum. But let's do a little more - now we will measure the period of oscillation digitally, using an acceleration sensor. This accelerometer can send data to your tablets. We should learn to read this data.
The sensor measures
So, we once again measured the period of oscillation of the pendulum. But this time digitally. It was also our first exposure to reading data from graphs.