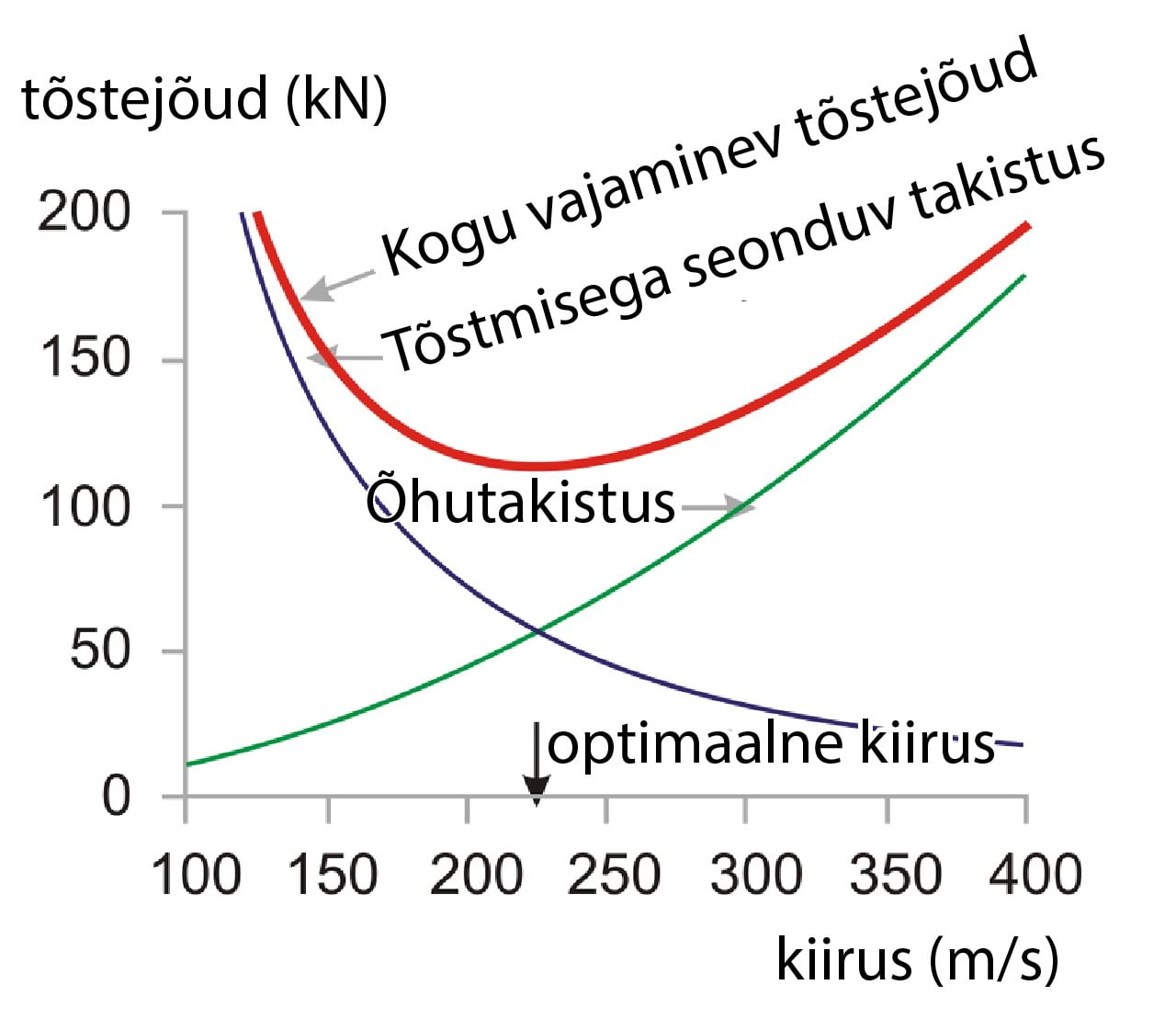
Joonis C.5: Lennuki liikumas hoidmiseks vaja minev energia sõltuvana kiirusest $v$ on takistusjõu $\frac{1}{2} c_d \rho A_pv^2$ – mis suureneb kiiruse kasvades – ja tõstmiseks kuluva jõu (tuntud ka kui indutseeritud takistus) $\frac{1}{2} \frac{(mg)^2}{ \rho v^2A_s}$ – mis väheneb kiiruse suurenedes – summa. Ón olemas kiirus $v_\text{optimaalne}$, mille korral vajalik jõud on minimaalne. Jõud on energia teepikkuse kohta, nii et minimiseerides jõu minimiseerime me ka teepikkuse kohta kuluva kütuse hulga. Et kütuse kasutust optimiseerida peame me lendama kiirusel $v_\text{optimaalne}$. See joonis näitab kilonjuutonites meie lihtsa mudeli hinnangut, millist jõudu on erinevate kiiruste $v$ korral tarvis $317$ tonni kaaluva, $64$-meetrise tiivaulatusega, $0,03$ takistuskoefitsiendiga ja $180\, \mathrm{m^2}$ esiosa pindalaga Boeing 474 lendamiseks, kui õhutihedus on $\rho = 0,41\, \mathrm{kg/m^3}$ ($10\, \mathrm{km}$ kõrgusel). Meie mudel pakub optimaalseks kiiruseks $v_\text{optimaalne} = 220\, \mathrm{m/s}$ ($540 \, \mathrm{miili/t}$). Õhusilindriga tegeleva mudeli jaoks on see võrdluses tegelikkusega väga hea tulemus!