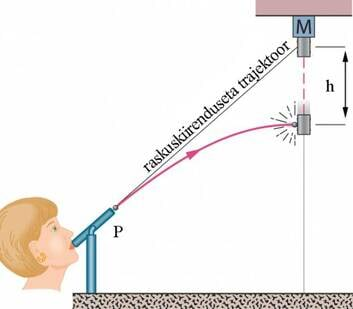
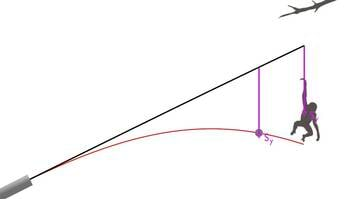
Puhkpüss on sihitud lakke riputatud raskusele. Raskus lastakse laest lahti täpselt lasu hetkel. Kui kõvasti peaks puhuma, et puhkpüssi kuul raskusele pihta saaks?

	Arvutianimatsioon eksperimendist.

Osutub, et raskus saab alati pihta. Seda saab tõestada nii matemaatiliselt kui eksperimentaalselt. Proovime kaasa mõelda.

Teeme kolm eeldust:

1. Lask peab toimuma täpselt siis, kui ahv oksast lahti laseb.
2. Püss peab olema sihitud ahvile. Joonisel vastab sellele sihile "raskuskiirenduseta trajektoor".
3. Kujutame ette, et ahv võib kukkuda igavesti, tema all pole maapinda.

Jagame kuuli kiiruse horisontaal- ja vertikaalkomponendiks (v_x ja v_y). Õhutakistust me ei arvesta. Seetõttu puudub horisontaalsuunalisele kiiruse komponendile takistav jõud, ning kiirus on konstantne (v_x on konstant). Ent nii ahvile kui kuulile mõjub Maa raskuskiirendus (v_y ei ole konstant), ehk lasu hetkel hakkavad mõlemad kehad kukkuma. Kui kuul liigub ülespoole, siis arvestame kukkumist kuuli otse liikumise trajektoori suhtes (vaata joonist).

Teeme mõttes kolm lasku.

1. Olgu esimese lastud kuuli algkiirus v₀ nii suur, et see jõuab praktiliselt kohe sihtmärgini. Ahv saab kohe pärast lasku pihta ning kummalgi kehal pole aega kukkuda. Lasule vastab joonisel raskuskiirenduseta trajektoor.
2. Teiseks lasuks vähendame natuke kuuli algkiirust. Nüüd jõuab kuul enne oksani jõudmist kukkuda. Et ahv laseb oksast lahti täpselt lasu hetkel, saab ahv kukkuda sama kaua kui kuul. Järelikult saab ahv taas pihta.
3. Kolmandaks lasuks vähendame kuuli algkiirust veelgi. Kuulil on nüüd rohkem aega kukkuda kui teisel lasul. Ent täpselt sama aja saab kukkuda ka ahv ning saab seetõttu kuuliga pihta.

Enam pole laske vaja sooritada, sest saame mõttekatsetest järeldada, et ahv saab sõltumata kuuli algkiirusest alati pihta. See juhtub eeldusel, et kuuli horisontaalne algkiirus on nullist suurem.