Küsimus on ... ebamäärane. Aga proovime selle sammhaaval meile tuntud füüsika raamistikku sobitada.
Tundub asjakohane küsimus. Sest, tõepoolest, mida me näeksime, kui me näeksime kosmost? Ja miks me peaksime kosmost just läbi korstna vaatama?
Kosmonaut, kes vaatab välja oma kosmoseaparaadi illuminaatorist, näeb midagi sellist.
Selline pilt ongi tehtud umbes 400 km kõrgusel.
Päeval taevasse vaadates näeme selgel päeval taevasina. Tõsi, öösel maalises keskkonnas taevasse vaadates on meile avanev pilt üsna sarnane sellega, mida näeb ISS-is päevatööd tegev kosmonaut. Aga küsimuses mainitakse ka korstent, küllap siis mõeldakse midagi muud.
On üsna hästi teada tõsiasi, et taevas paistab sinine, sest sinine valgus hajub õhuosakestelt kõige tugevamalt ning seda satub seetõttu maapealse vaatleja silma rohkem.
Nii et kui korstnas ei oleks õhku, siis oleks põhimõtteliselt võimalik näha seda, mida kosmonaudidki - musta taevalaotust.
Järeldus: korstnas ei tohiks olla õhku ... pilvedest rääkimata.
Küsimuses on mainitud vaid korstna kõrgust, aga defineerimata jääb selle diameeter või väliskuju. Eeldame siis, et tegemist on tavalise korstnaga, st olgu selle läbilõige ringikujuline. Eeldame ka, et korsten on ikka korsten, st et selle diameeter on selline, nagu korstnatel ikka on.
Leppisime kokku, et korstna sees õhku ja kui korsten on tõepoolest 400 m kõrgune siis selle sees üles vaadates võikski näha musta laiku ja mõnd tähte, st kosmost? Lootused on seda suuremad, et korstna seinad varjavad ära kogu segava valguse.
Muidugi, korsten ise on ka takistuseks - selle seinad varjavad ära ka enamuse vaateväljast.
Äkki küsija sellele mõtleski?
Järeldus: tuleks mõelda, mida me näeksime, kui vaataksime sisse 400 m pikkusesse torusse.
Mõtleme nüüd inimese silmast, sest ülesandes on juttu nägemisest.
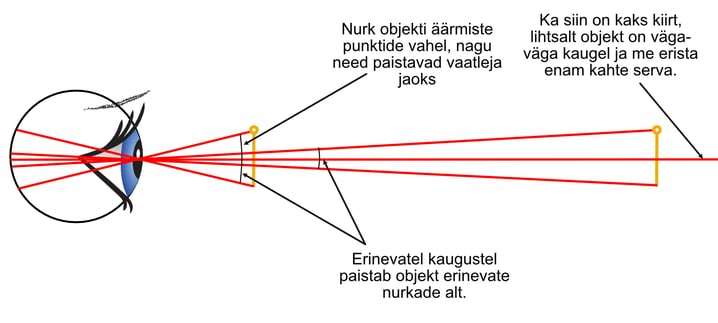
Teame, et me väga väikseid asju ei näe. Ja olukord paraneb, kui toome objekti silmale lähemale ning halveneb, kui viime selle kaugemale.
Selles ülesandes on objektiks korstna suu, st selle kõige ülemine ots.
Wikipedia ütleb, et inimese nägemise nurklahutus on üks kaareminut ehk umbes 0.017°. Ja et kui objekt on ühe kilomeetri kaugusel, vastab sellele objekti diameeter 0,3 m. Mis tähendab, et kilomeetri kaugusel olevat 0,2 m diameetriga objekti me ei näe - silma nurklahutus ei ole piisav.
Järeldus: tuleks arvutada, millise diameetriga korstna suud me 400 km kaugusel üleüldse näha võiksime.
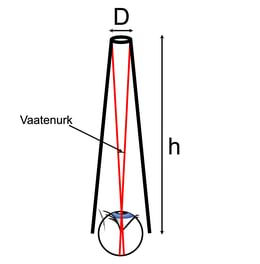
-korstna kõrgus
- korstna otsas oleva augu diameeter
- minimaalne nurk kahe valguskiire vahel, mida inimsilm suudab veel eristada (silma nurklahutus)
| Vaatenurk (rad) | (*) |
| Minimaalne vaatenurk kraadides | (**) |
Tasuks ehk arvutada, milline peaks olema 400km kõrguse korstna otsa diameeter selleks, et seda oleks veel võimalik näha.
Arvutamiseks eeldame, et vaatenurk on võimalikest minimaalne. Avaldame valemist (*) diameetri ja arvutame
Selle ülesande juures on lisaks optikale teisigi aspekte, mille üle on põnev juurelda. Näiteks õhurõhk.
Sest kui ka korsten on piisavalt suure diameetriga, et sealt "kosmost näha", siis see tähendab automaatselt seda, et korstnas ei ole õhku ning puudub ka jõud, mis tasakaalustaks väljaspoolt korstnale mõjuvat õhurõhust põhjustatud jõudu.
Vaatlejal on vaja väga tugevat korstent.