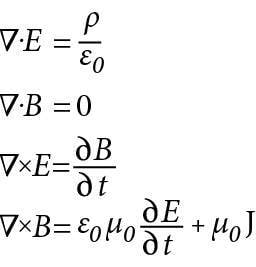Elektromagnetism
- 1 Elektriväli ja magnetväli
- Sissejuhatus
- 1.1 Elektromagnetismi uurimisaineLisamaterjalid
- 1.2 ElektrilaengLisamaterjalidLisaülesanded
- 1.3 Coulomb'i seadusKontrollküsimusedLisamaterjalid
- 1.4 Ampère seadusKontrollküsimusedLisamaterjalid
- 1.5 Elektrivälja tugevus ja magnetinduktsioonKontrollküsimusedLisamaterjalid
- 1.6 Väljade visualiseerimineKontrollküsimusedLisamaterjalid
- 1.7 Elektrivälja potentsiaal ja pingeKontrollküsimusedLisamaterjalid
- 1.8 Elektriväli ja magnetväli - lõpetuseks
- 2 Elektromagnetväli
- Sissejuhatus
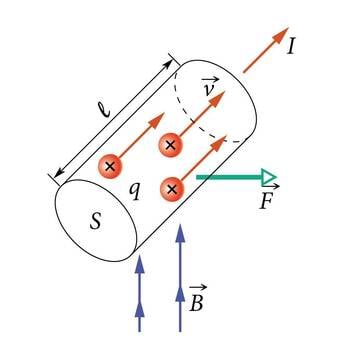
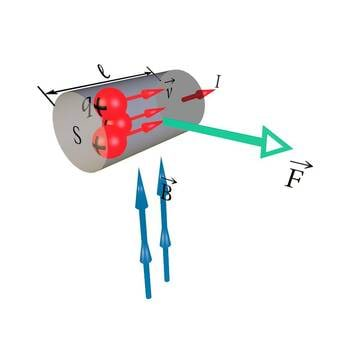
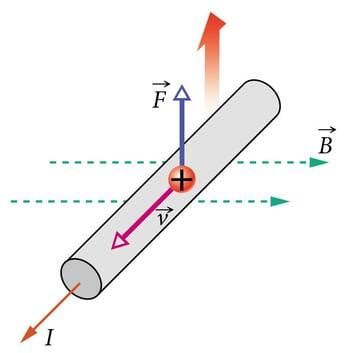
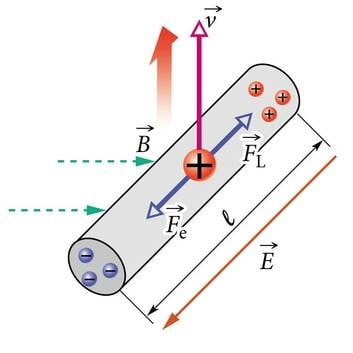
- 2.1 Ühele osakesele mõjuv magnetjõudKontrollküsimusedLisamaterjalid
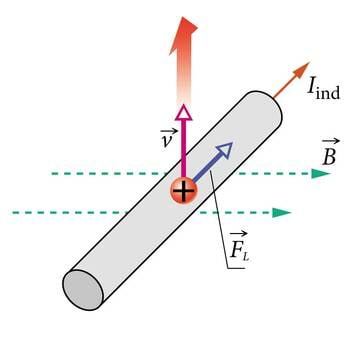
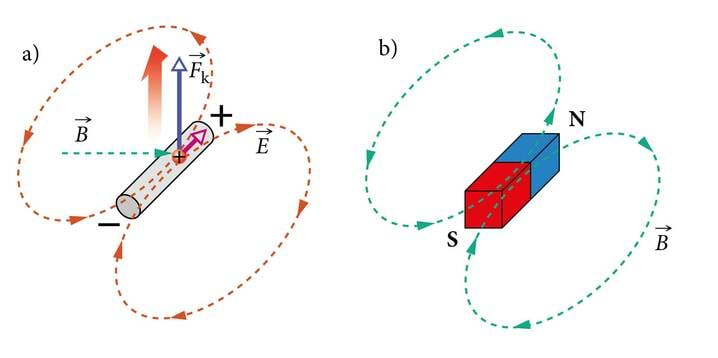
- 2.2 Pööriselektriväli ja induktsiooni elektromotoorjõudKontrollküsimusedLisamaterjalid
- 2.3 Faraday katsedKontrollküsimusedLisamaterjalid
- 2.4 Faraday induktsiooniseadusKontrollküsimusedLisamaterjalid
- 2.5 Lenzi reegel. Induktsiooniseaduse rakendusedKontrollküsimusedLisamaterjalid
- 2.6 Induktiivsus ja mahtuvusKontrollküsimusedLisamaterjalid
- 2.7 Elektromagnetvälja energiaKontrollküsimusedLisamaterjalid
- 2.8 Elektromagnetiline levitatsioonLisamaterjalid
- 2.9 Lõpetuseks - elektromagnetväli
- 3 Elektromagnetlained
- Sissejuhatus
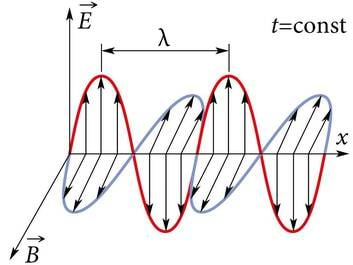
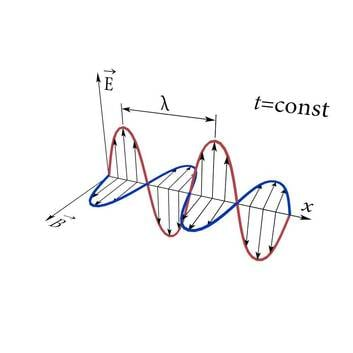
- 3.1 Elektromagnetvälja levik elektromagnetlainetenaKontrollküsimusedLisamaterjalid
- 3.2 Valguse kirjeldamineKontrollküsimusedLisamaterjalid
- 3.3 Elektromagnetlainete omadusedKontrollküsimusedLisamaterjalid
- 3.4 Polariseeritud valgusKontrollküsimusedLisamaterjalid
- 3.5 Lõpetuseks - elektromagnetlained
- 4 Valguse ja aine vastastikmõju
Miks on otsene välgutabamus harilikult surmav? Kas äikese ajal tuleks puu alla varju ronida või lagedal väljal seista? Kas mõistlikum on rahulikult seista, kükitada või joosta? Miks inimestel juuksed püsti tõusevad, kas see on ohu märk? Miks on äikesetormi ajal lehmad, hobused ja lambad tavaliselt suuremas ohus kui inimesed?
On palju lugusid sellest, kuidas kuulus USA teadlane ja riigimees Benjamin Franklin lennutas läheneva äikesetormi ajal tuulelohet, et näidata selle loodusnähtuse elektrilisi omadusi. Miks välk teda ei tapnud?
Kas äikesepilve saaks põhimõtteliselt ka kompassiga leida?
Tänapäeval ümbritsevad meid kõikjal esemed ja nähtused, mille iseloomustamisel kasutame sõna elekter. See sõna on jõudnud meieni kreeka keelest. Nii nimetasid vanad kreeklased kuldse läikega metallisulamit ja ka sellega väliselt sarnast ainet – merevaiku (kr - elektron). Nad märkasid, et villase riidega hõõrutud merevaigutükk suudab kergeid ainekübemeid enda külge tõmmata. Ajapikku hakati kõiki selliseid loodusnähtusi nimetama merevaigu-sarnasteks ehk elektrilisteks.
Kreeka päritoluga on ka sõna magnet. Magnesia kivina (kr - Magnetis lithos) tunti vanas Kreekas kivimit, mis oli suuteline raudesemeid enda külge tõmbama. Elektrilise ja magnetilise tõmbejõu sarnasusest lähtuvalt oli vana- ja keskajal kombeks arvata, et need jõud põhimõtteliselt ei erinegi. Alles uusaegsetes esimestes teaduslikes käsitlustes hakati elektri- ja magnetnähtusi selgelt omavahel eristama. 19. sajandi keskel avastati, et elektrilistel ja magnetilistel jõududel on siiski ühine allikas. Elektri- ja magnetnähtused on looduses toimiva üldise elektromagnetilise vastastikmõju avaldumisvormid. Jõud, millega me oma igapäevases elutegevuses vältimatult kokku puutume, on valdavalt elektromagnetilise päritoluga. Nendeks on näiteks elastsusjõud, hõõrdejõud ja ka elusorganismide lihasjõud. Elektrijõud hoiavad koos lihtaine aatomeid. Vedeliku või gaasi molekulideks, tahkisteks ja keerulisteks orgaanilisteks ühenditeks liidab aatomeid keemiline side, mis on samuti tingitud elektromagnetilisest vastastikmõjust.
Elektromagnetjõudude kaks tähtsaimat tehnilist rakendust on elektroenergeetika ning elektriline side- ja infotehnika. Elektroenergeetika hõlmab kogu inimtegevust elektrienergia tootmisel, ülekandel ja kasutamisel. Elektrijaamades muudetakse elektrienergiaks mingi osa kütuse põlemisel vabanevast soojusest, voolava vee kineetilisest energiast või koguni aatomituumade seoseenergiast. Neid jaamu nimetatakse seetõttu vastavalt soojus-, hüdro- ja tuumaelektrijaamadeks. Päikesepatarei muundab elektrienergiaks valguskiirguse energiat. Taskulambipatareis, autoakus ja teistes keemilistes vooluallikates saadakse elektrienergiat keemilisel reaktsioonil vabaneva energia arvelt.
Tarvitis leiab aset vastupidine protsess. Elektrienergia muundub mehaaniliseks energiaks (elektrimootoris), valguskiirguse energiaks (elektrilambis), soojuseks (kütteseadmes) või mingiks muuks energia liigiks. Elektrienergia on mugav vahelüli loodusest ammutatava ja inimtegevuses kasutatava energia vahel. Seda soodustab asjaolu, et elektrienergiat saab üle kanda juhtmete abil. Pole vaja mingeid rihmu, võlle ega hammasrattaid.
Elektrienergia suurima puudusena võiks nimetada raskusi suurte energiakoguste salvestamisel. Elektrilise energia tootmine ja tarbimine peavad toimuma samaaegselt.
Elektroenergeetikast veelgi kiiremini areneb tänapäeval elektromagnetiline infotehnika. See hõlmab andmete, kõne, muusika või muu sellise esitamist ja ülekandmist elektromagnetilise signaalina. Samas on ka tegemist info elektrilise, magnetilise või optilise salvestamise ning töötlemisega. Elektriliste infotöötlus- ja sidesüsteemide kiiretoimelisuse aluseks on elektromagnetilise vastastikmõju suur levimiskiirus – kuni 3·108 m/s.
Käesolev õpik käsitleb elektromagnetilise vastastikmõju seaduspärasusi, mille tundmine aitab meil mõista väga paljude loodusnähtuste tekkimist. Nendel seaduspärasustel põhineb ka elektriliste ja optiliste seadmete töö, mida me oma igapäevases elus pidevalt kasutame. Seega on vastavad teadmised nii tunnetusliku kui ka rakendusliku väärtusega.
Elektromagnetismi teadusliku uurimise algatajaks peetakse Inglise arsti ja füüsikut William Gilbertit. Aastal 1600 ilmus trükist tema töö De magnete..., mille täieliku pealkirja võib eesti keelde tõlkida kujul: Magnetist, magnetilistest kehadest ja suurest magnetist – Maast. Gilbertist oli juttu juba põhikooli Elektriõpetuses. Seal mainiti ka Benjamin Franklinit, kes lõi esimese tervikliku elektrinähtuste teooria, esimest bioelektromagnetismi uurijat Luigi Galvanit ning esimese vooluallika loojat Alessandro Voltat. Põgusalt oli juttu Ohmi seaduse avastajast Georg Simon Ohmist ning voolu magnetvälja esmauurijast Hans Christian Örstedist.
Käesolevas kursuses on aga aukohal elektrostaatika põhiseaduse formuleerija Charles Coulomb, magnetostaatika põhiseaduse formuleerija André Marie Ampère, elektromagnetilise induktsiooni avastaja Michael Faraday ning kõiki elektromagnetnähtusi kirjeldava ühtse teooria looja James Clerk Maxwell. Eestimaalt pärit mehena pälvib meie erilist tähelepanu ka Emil Lenz, induktsioonivoolu suunda määrava reegli formuleerija.
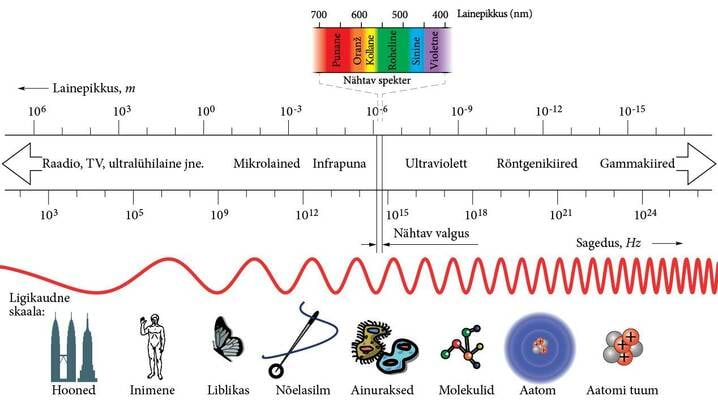
Valgusnähtuste teaduslik käsitlus sai alguse 17. sajandil, kui I. Newton püstitas hüpoteesi valgusest kui silmale nähtamatute osakeste voost, mis levivad ühtlases keskkonnas sirgjooneliselt. Neid osakesi nimetas ta korpuskuliteks, mida võib pidada nüüdisaegsete kvantide eelkäijateks.
Mõned aastad pärast Newtonit püstitas C. Huygens teise hüpoteesi, mille kohaselt valgus levib lainetena. Ta arvas, et valguslaine levimiseks on vajalik mingi eriline keskkond, mis täidab kogu universumi. Seda ainet nimetati eetriks. Tänapäeval on teada, et mingit erilist, valguse levimiseks vajalikku keskkonda ei eksisteeri ja valgus levib ka tühjuses.
Aastal 1802 tegi T. Young katseid, mis näitasid, et kitsast avast läbi minnes kaldub valgus oma esialgsest levimissuunast kõrvale, valguse teel oleva tõkke taha. Kuna veelained levivad ka tõkete, näiteks kivide taha, siis Youngi katse tõestas, et valgusel on laineline olemus.
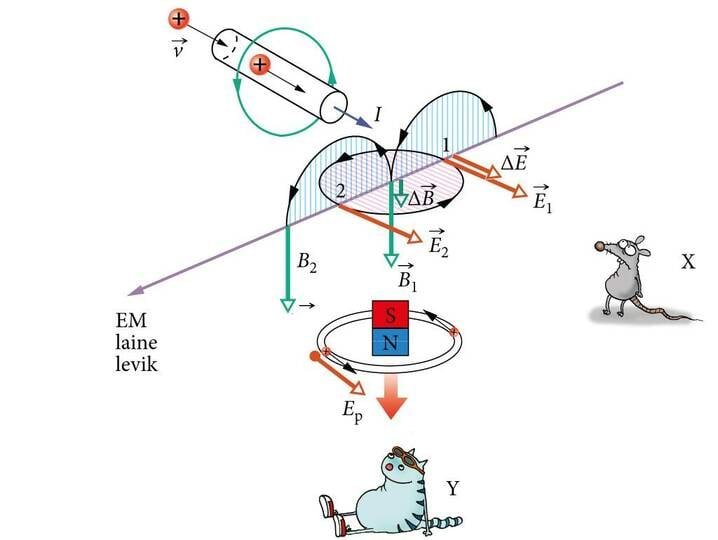
Järgmise olulise sammu valguse laineteoorias tegi J. C. Maxwell, kes 1865.a. tõestas teoreetiliselt, et on olemas elektromagnetlained, mis levivad ka tühjuses ja seda kiirusega 3·108 m/s. See tulemus langes küllalt hästi kokku tolleks ajaks määratud valguse kiirusega. Sellest järeldas Maxwell, et valgus on elektromagnetlaine.
Nüüdisaegsele valguse kvantteooriale pani aluse 1900.a. M. Planck, kes võttis kasutusele valgusosakesed ehk kvandid. Muidu ei suutnud ta teoreetiliselt seletada tahkete kehade kiirgusspektreid. Planck pidas kvante vaid teooriat lihtsustavateks abivahenditeks.
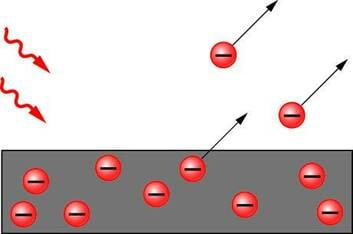
A. Einstein näitas 1905.a., et kvandid on reaalselt olemas, sest ta seletas nende abil ära fotoefekti katsed, mida laineteooria ei suutnud seletada.
Sellest alates on selge, et valgusnähtusi pole võimalik kirjeldada ainult lainete või ainult osakeste abil. On nähtusi, mida saab seletada lainete abil ja teisi nähtusi saab seletada kvantide abil. On ka selliseid nähtusi, mida saab seletada nii lainete kui kvantide abil. Tutvume nendega põgusalt ka käesoleva kursuse raames.
Me alustame elektromagnetismi õppimist tutvumisest staatilise ehk ajas muutumatu elektrivälja ning magnetväljaga. Saame teada, mida on nende kahe välja kirjeldustes ühist ja mida erinevat. Tutvume kummagi välja põhiseadusega (Coulomb’i ja Ampère'i seadused) ning peamiste neid välju iseloomustavate vektorsuurustega, milleks on elektrivälja tugevus E ja magnetinduktsioon B. Kursuse teises osas vaatleme elektri- ja magnetvälja muutumist ajas. Elektromagnetilise induktsiooni nähtuse uurimisel selgub meile, et elektriväli ja magnetväli on ühtse elektromagnetvälja kaks piirjuhtu. Tutvume ka välja energiat salvestavate seadmetega, milleks elektrivälja korral on kondensaator ja magnetvälja puhul induktiivpool. Kursuse kolmandas osas uurime elektromagnetvälja levikut elektromagnetlainetena. Vaatleme valguse tekkimisel ja kadumisel ilmnevaid valguse osakese-omadusi ning valguse levimisel avalduvaid laineomadusi. Õpime kirjeldama vastavaid optilisi nähtusi: interferentsi, difraktsiooni ja polarisatsiooni. Kursuse neljandas osas vaatleme valguse ja aine vastastikmõju. Põhiteemadeks on geomeetriline ehk kiirteoptika, valguse levimiskiiruse erinev muutumine eri ainetes ja valguse tekkeprotsessid. Käsitleme valguse kahte peamist tekkemehhanismi: soojuskiirgust ja luminestsentsi.
Lihtsaim elektrinähtus, mida me kõik kindlasti kogenud oleme, seisneb kehade elektriseerumises nende vastastikusel hõõrdumisel. Elektriseerunud kehade vahel mõjub jõud. Näiteks liibub kuivale nahale kunstkiust valmistatud särk. Pärast pestud ja kuivade juuste kammimist tõmbuvad juuksed kammi külge. Elektriseerunud kehade kohta öeldakse ka, et nad on laadunud või omandanud elektrilaengu.
Elektrilaeng ehk edaspidi lihtsalt laeng (tähis q või Q) on mingit keha iseloomustav füüsikaline suurus. Laeng näitab, kui tugevasti keha osaleb elektromagnetilises vastastikmõjus. Laengu olemasolu kehal saab kindlaks teha vaid elektri- ja magnetjõudude põhjal.
Sõna laeng kasutatakse õige mitmes tähenduses. Esiteks nimetatakse laenguks keha omadust osaleda elektromagnetilises vastastikmõjus. Rääkides elementaarosakese laengust, peame silmas selle osakese omadust osaleda elektri- ja magnetnähtustes. Sõna laeng teine tähendus on nimetatud omadust kirjeldav füüsikaline suurus. Kõneldes laengu suurusest, rõhutame laengu mõõtmise võimalikkust. Laengu kui suuruse mõõtmine on aga tegelikult kehade võrdlemine nende laengu kui omaduse põhjal. Peale selle mõistetakse füüsikas laengu all ka niisuguste osakeste kogumit, millel on olemas laeng kui omadus. Näiteks räägitakse ruumi mingis osas paiknevast laengust või siis laengu liikumisest. Neid väljendeid tuleb aga käsitleda lühenditena. Tegelikult on jutt ikkagi laengut omavate osakeste paiknemisest või liikumisest.
Juba 9. klassi Elektriõpetusest teame, et looduses on kahte liiki laenguid. Neid on kokkuleppeliselt hakatud nimetama positiivseteks ja negatiivseteks. Selline nimetusviis võimaldab laengu liiki väljendada märgiga arvväärtuse ees (+ või –).
Meile mehaanika kursusest tuttav gravitatsioonijõud on ainult tõmbejõud. Samas tuntakse ka vaid ühte liiki “gravitatsioonilaengut”, mida on kombeks nimetada massiks. Elektrijõud võivad aga olla nii tõmbe- kui tõukejõud. Seega peab ka laenguid olema kahte liiki. Laengu arvväärtus määrab jõu suuruse, märk aga suuna. Samanimeliselt laetud kehade vahel mõjub tõukejõud, erinimeliste laengute korral aga tõmbejõud.
Elektrit mittejuhtiva niidi otsas rippuvat kerget metallfooliumist keha nimetatakse sageli elektripendliks. Ka meie toimime edaspidi nii.
Füüsikalise looduskäsitluse aluste (FLA) kursuses õpitud atomistliku printsiibi põhjal teame, et ainel on olemas osakesed, mis pole jagatavad veel väiksemateks osakesteks. Kuna laeng on osakese omadus, siis ei tohiks ka laeng olla kuitahes väike.
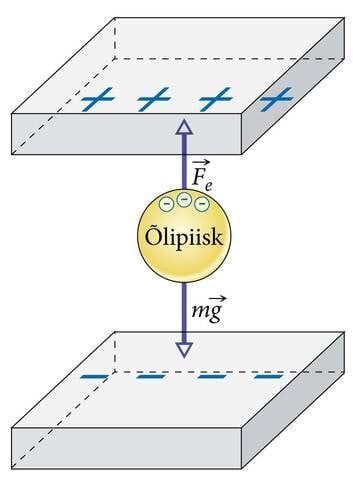
| J.1.3 Robert Andrews Millikani katse on oma olemuselt ühtaegu lihtne ja geniaalne - väga väikeste laengute mõõtmiseks on väga raske leida piisavalt tundlikku mõõteriista. Aga elementaarlaengutele mõjuvat elektrijõudu oli võimalik võrrelda õlipiiskadele mõjuva raskusjõuga. | Robert Andrews Millikani katse on oma olemuselt ühtaegu lihtne ja geniaalne - väga väikeste laengute mõõtmiseks on väga raske leida piisavalt tundlikku mõõteriista. Aga elementaarlaengutele mõjuvat elektrijõudu oli võimalik võrrelda õlipiiskadele mõjuva raskusjõuga. |
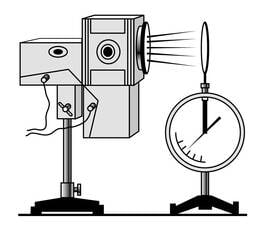
Laengu jagatavuse küsimust asus 20. sajandi algul uurima ameerika füüsik Robert Andrews Millikan. Ta vaatles mikroskoobi abil tillukesi laetud õlipiisku, millele mõjus vertikaalselt üles suunatud elektrijõud. Kui see jõud tasakaalustas piisa raskusjõu, jäi piisk mikroskoobi vaateväljas seisma.
Olles mõõtnud piisa ruumala ning teades õli tihedust, suutis Millikan määrata piisa massi ja raskusjõu, järelikult ka elektrijõu. Selle põhjal leidis Millikan piisa laengu. Ta märkas peagi, et kõik tema katsetulemused olid mingi kindla laengu väärtuse täisarv-kordsed.
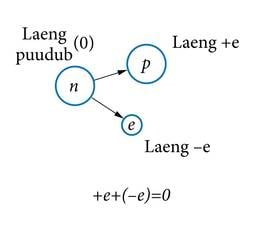
Vähimat katseliselt tuvastatavat laengu väärtust on hakatud nimetama elementaarlaenguks (e). 20. sajandil tehti kindlaks, et kõigi ainete aatomid koosnevad prootonitest, neutronitest ja elektronidest. Prootonid ja neutronid moodustavad aatomi tuuma, mille ümber liiguvad elektronid. Prootonil on laeng +e, elektronil –e, neutronil laeng puudub. Seega on iga keha laengu suurus nende osakeste laengute summa.
Keemiast teame, et aatomi tuum käitub keemilistes reaktsioonides stabiilse tervikuna. Aatomi kuuluvus kindlale elemendile on määratud prootonite arvuga tuumas. Neutraalses aatomis on elektrone ja prootoneid ühepalju. Elektronide lisandumisel aatomisse moodustub negatiivne ioon ja elektronide lahkumisel positiivne ioon. See võimaldab mõista kehade elektriseerumist hõõrdumisel. Sõltuvalt vastavate ainete aatomite ehitusest võivad väliskihi elektronid ehk valentselektronid ühelt kehalt teisele üle minna. Keha, mis saab elektrone juurde, laadub negatiivselt. Seevastu keha, millelt elektronid ära rebiti, laadub positiivselt, sest tema aatomituumade positiivne laeng on osaliselt tasakaalustamata. Elementaarlaenguga osakeselt ei saa tema laengut ära võtta nii nagu elektriseerimisel rebitakse kehalt lahti elektrone. Laeng on osakesele sama kindlalt omane suurus nagu mass. Kui näiteks elektronil ei oleks laengut –e, siis ta polekski enam elektron. Negatiivse elementaarlaengu olemasolu on üks tunnustest, mis määrab elektroniks nimetatava osakese. Elementaarlaengu jagamatuses avaldub atomistlik printsiip.
Mehaanikast teame, et impulss ja energia on suletud süsteemis jäävad suurused. Elektrinähtuste uurimisel selgub, et ka elektrilaeng on jääv. Laeng ei teki ega kao. Kehade süsteemi kogulaeng saab muutuda vaid laetud osakeste sisenemisel süsteemi või väljumisel sellest. Kui laetud osakeste niisugust liikumist ei toimu, nimetatakse süsteemi elektriliselt isoleerituks. Tegemist on tüüpilise suletud süsteemiga. Selle mõistega tutvusime juba Füüsikalise looduskäsitluse aluste kursuses.
Laengu jäävuse seadust pole kuigi lihtne rangelt tõestada. Vastavas katses peaks ju mõõtemääramatus olema väiksem elementaarlaengust. Paljud erinevad elektrinähtused on aga seletatavad vaid lähtudes laengu jäävusest. Seetõttu usuti laengu jäävuse seaduse kehtivusse juba ammu enne elektronide ja prootonite avastamist.
Selgeid viiteid laengu jäävuse seadusele leiame keemiast. Tervikuna neutraalne keedusoola (NaCl) kristall dissotsieerub lahustumisel vees positiivseteks naatriumi ja negatiivseteks kloori ioonideks (Na+ ja Cl–), mida tekib ühepalju.
Laengu jäävuse seadus sai füüsikas lõpliku kinnituse alles osakeste vahel toimuvate muundumisreaktsioonide uurimisel. Selgus, et laetud osakeste teke või kadumine nendes reaktsioonides on võimalik vaid paarikaupa. Uue positiivse osakese tekkimisel ilmub ka negatiivne osake. Nii näiteks tekivad vaba neutroni lagunemisel üheaegselt positiivne prooton ja negatiivne elektron (J.1.4). Neutron ongi siin see elektriliselt isoleeritud süsteem, millest oli juttu eespool.
Laengu jäävus väljendab maailma üldist keskmist elektrilist neutraalsust. Kujutlegem hetkeks, mis juhtuks, kui kõigis kehades oleksid ühte liiki laenguga osakesed ülekaalus. Sel juhul mõjuksid ju kõigi kehade vahel elektrilised tõukejõud. Seda me aga looduses ei näe. Meid ümbritsevad kehad on tavaliselt neutraalsed. Positiivse ja negatiivse laenguga osakesi on neis ühepalju. Kui üks keha saab positiivse laengu, siis laadub mingi teine keha negatiivselt. Kehade laengute summa jääb muutumatuks. Aga see ju ongi laengu jäävus.
Niisiis kehtib laengu jäävuse seadus: elektriliselt isoleeritud süsteemi kogulaeng on jääv suurus.
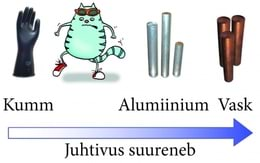
Hõõrdeelektrit uurides märkame kohe, et ained erinevad oma elektrijuhtivuse poolest. Kui näiteks kuivad juuksed kammi külge tõmbuma hakkavad, siis võime sellest jagu saada kammi niisutades. Seega on kraanivesi elektrit juhtiv aine. Läbi tema lahkuvad laetud osakesed kammilt. Puhas (destilleeritud) vesi aga ei juhi elektrit. Samuti ei õnnestu meil tavaliselt hõõrumise teel laadida märgi esemeid ja metallkehi, sest tasakaalustamata laeng lahkub neilt. Laenguga osakesed liiguvad läbi eseme ja seejärel läbi meie käte.
Inimkeha juhib elektrit suhteliselt hästi. Metalleset ei õnnestu hõõrumise teel elektriseerida just seetõttu, et nii ese kui ka seda hoidev käsi juhivad elektrit. Olles tõmmanud kätte kummikinda, võime elektriseerida ka metalleset. Kummi elektrit ei juhi ning laeng püsib esemel.
Põhikooli Elektriõpetusest teame, et metall ja kraanivesi sisaldavad arvukalt liikumisvõimelisi laetud osakesi ehk vabu laengukandjaid. Sõnaga vaba tähistame seejuures laetud osakese võimet liikuda elektrijõudude toimel kogu vaadeldava keha või ainekoguse piires. Nagu kõik aineosakesed, nii osalevad ka laengukandjad kaootilises soojusliikumises. Kui aga neile mõjub kindla suunaga elektrijõud, hakkavad nad täiendavalt liikuma ka selle jõu mõjul.
Vabade laengukandjate sisalduse järgi jagunevad ained kolme rühma: juhid, dielektrikud (ehk mittejuhid või ka isolaatorid) ja pooljuhid.
Juhid on ained, milles vabade laengukandjate arv on väga suur. See ei erine oluliselt aatomite (või molekulide) üldarvust. Tüüpilised juhid on metallid, kuna valentselektronid pole neis seotud ühegi kindla aatomiga ja on järelikult vabadeks laengukandjateks. Elektrit juhtivates vedelikes (näiteks kraanivees) täidavad vabade laengukandjate osa keemiliste lisandite ioonid.
Dielektrikud ehk mittejuhid sisaldavad väga vähe vabu laengukandjaid ning seetõttu on neis tekkiv elektrivool reeglina väga nõrk. Vabade laengukandjate puudumine gaasilises või vedelas dielektrikus on enamasti põhjustatud sellest, et dielektriku aatom või molekul on elektriliselt neutraalne süsteem. Elektrijõud ei suuda laetud osakesi sellest süsteemist välja rebida. Tahke dielektrik võib küll koosneda erimärgiliselt laetud ioonidest, aga elektrijõud ei suuda neid liikuma panna.
Pooljuhid on saanud oma nime vahepealse elektrijuhtivuse järgi juhtide ja dielektrikute kui kahe äärmuse vahel. Laengukandjad ei ole pooljuhtides küll alati vabad, kuid neid saab suhteliselt kergesti vabadeks muuta. Seetõttu on pooljuhtidele iseloomulik vabade laengukandjate arvu tugev sõltuvus temperatuurist, pealelangevast valgusest, lisandite sisaldusest põhiaines jne. Pooljuhi elektrijuhtivus on nende tingimuste muutmise teel reguleeritav. See pooljuhtide väärtuslik omadus leiab laialdast kasutamist nüüdisaegses elektroonikas.
Kindlaid piire ainete kolme rühma vahel pole. Näiteks on metallis vabade laengukandjate arv aatomite üldarvust tavaliselt suurem, sest aatomil võib olla väliskihis mitu elektroni, mis saavad muutuda vabadeks laengukandjateks. Ainet loetakse aga juhiks veel ka siis, kui mitme tuhande aatomi või molekuli kohta tuleb vaid üks vaba laengukandja. Nii on see näiteks kraanivee korral. Pooljuhtides on vabade laengukandjate arv aatomite arvust väiksem ligikaudu miljon korda, dielektrikutes aga reeglina üle miljardi korra.
Veel tuleb märkida, et sõna juht kasutatakse nii elektrit juhtiva aine kui ka sellest ainest valmistatud keha tähistamiseks.
Laengukandjate suunatud liikumist nimetatakse elektrivooluks.
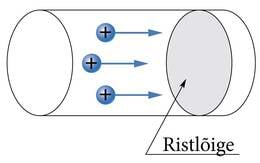
Voolu tekkimiseks on vajalik nii vabade laengukandjate olemasolu kui ka nende liikumist põhjustav jõud. Elektrivoolu iseloomustavaks suuruseks on voolutugevus I. Voolutugevus näitab, kui suur laeng läbib ajaühikus juhi ristlõiget
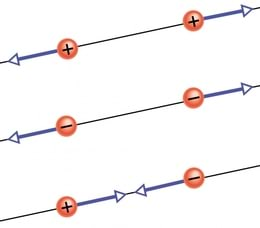
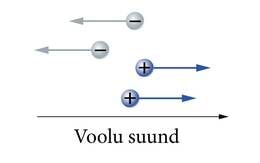
Ristlõike all mõistetakse seejuures voolu suunaga ristuva lõike pinda (J.1.5). Voolu suunaks on kokkuleppeliselt valitud positiivsete laengukandjate liikumise suund. Negatiivsed laengukandjad (näiteks elektronid metallis) liiguvad seega voolu kokkuleppelisele suunale vastupidises suunas (J.1.6).
On oluline mõista, et pole üldse tähtis, kumma märgiga laengukandjad reaalselt aines liiguvad. Nii positiivsete laengukandjate liikumine paremale kui negatiivsete liikumine vasakule joonisel 1.6 tähendab üht ja sedasama voolu suunda. Liikuvate laengukandjate märgi määramine on võimalik vaid keerulisemates katsetes. Tavalise vooluringi korral me laengukandjate märki teada ei saagi, aga see asjaolu ei sega vooluringide uurimist.
Voolutugevuse ühikuks on üks amper (1 A). Amper on SI elektriline põhiühik. See tähendab, et kõik teised elektriliste suuruste mõõtühikud tuletatakse tema abil. Amper defineeritakse vooluga juhtmete magnetilise vastastikmõju kaudu (p.1.4.2). Voolutugevuse I leidmiseks peame juhi ristlõiget läbiva laengu q jagama selleks kuluva ajaga t (valem 1.1 ). Laeng ise on seega esitatav voolutugevuse ja aja korrutisena
Viimase seose põhjal on defineeritud elektrilaengu SI-ühik üks kulon (1 C). Kui voolutugevus juhis on üks amper, siis läbib ühe sekundi jooksul juhi ristlõiget laeng suurusega üks kulon. Järelikult
Elementaarlaengu väärtus on 1,6021892·10-19 kulonit. Praktilistes arvutustes piisab reeglina täpsusest
Üks kulon on väga suur laeng. Kammi või klaaspulka elektriseerides anname talle laengu, mille suurusjärk on üks nanokulon kuni üks mikrokulon (1 μC = 10-6 C). Tabelis 1.1 on toodud mõned iseloomulikud voolutugevused.
|
Elektrinähtus või elektriseade |
Voolutugevus |
|
Biovoolud elusorganismides |
alla 10-6 A |
|
Raadio, CD-mängija, muusikakeskus |
0,01 – 0,1 A |
|
Võrgutoitega elektrilambi või taskulambi hõõgniit |
0,2 – 0,5 A |
|
Autolaterna hõõgniit, tänavavalgusti |
1 – 5 A |
|
Elektripliidi või soojapuhuri küttekeha |
2 – 20 A |
|
Trammi või elektrirongi mootor, auto käiviti |
100 – 500 A |
|
Keevitusagregaat |
100 – 1000 A |
|
Välgu helendav kanal |
kuni 106 A |
Maksimaalset laengut, mille vooluallikas suudab vooluringist läbi viia, nimetatakse sageli vooluallika mahutavuseks (mitte mahtuvuseks!) ja teda mõõdetakse amper-tundides. Kui voolutugevus juhis on üks amper, siis läbib ühe tunni jooksul juhi ristlõiget laeng üks amper-tund (1 A·h).
Kuna ühes tunnis on 3600 sekundit, siis 1 A·h = 1 A·3600 s = 3600 C.
Leiame, millise aja jooksul suudab auto käivitit toita aku, mille mahutavus on 50 A·h. Käiviti tarbib voolu 200 A.
Lahendus
Arvutused:
Aku mahtuvuseks leiame
Valemist 1.1 saame
Seega
Vastus: Aku suudab käivitit toita maksimaalselt 900 sekundi ehk 15 minuti jooksul.
Igaüks, kes autodega lähemalt kokku on puutunud, teab hästi, et tegelikult ei saa käivitil nii kaua töötada lasta. Miks see nii on, selgub Energia kursuses.
Laeng
Laeng on füüsikaline suurus, mis näitab, kui tugevasti keha osaleb elektromagnetilises vastastikmõjus.
Kahte liiki laengud
Looduses leidub kahte liiki laenguid, mida nimetatakse positiivseteks ja negatiivseteks (+ ja –). Samamärgiliselt laetud kehade vahel mõjub tõukejõud, erimärgiliselt laetud kehade korral aga tõmbejõud.
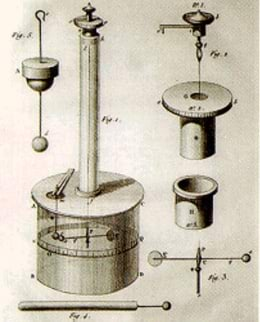
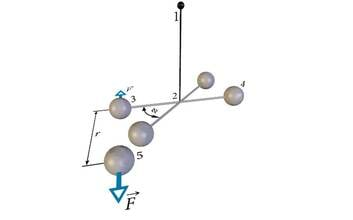
Elektrijõude asus 1784. aastal mõõtma Charles de Coulomb. Mõõteseadmena kasutas ta väändkaalu ehk torsioonkaalu. Väändkaalu töö aluseks on mõõdetava jõu võrdlemine peenikese traadi väändel tekkiva elastsusjõuga.Coulomb’i poolt kasutatud väändkaalu korral (J.1.7) rippus traadi (1) küljes horisontaalne mittejuhtiv varras (2), mille ühes otsas paiknes uuritav metallkuulike (3), teises otsas aga kuulikest tasakaalustav raskus (4). Vardaga ristuva jõu rakendumisel kuulikesele pöördus varras seni, kuni traadi väände elastsusjõud tasakaalustas kuulikesele mõjuva jõu. Coulomb tegi kindlaks, et nurk j, mille võrra varras joonisel punktiiriga kujutatud tasakaaluasendist välja pöördus, oli võrdeline jõuga. See võimaldas pöördenurga kaudu jõudu mõõta. Oma katsete korraldamisel lähtus Coulomb eeldusest, et varda küljes paikneva, algselt neutraalse kuulikese (3) puudutamisel teise täpselt samasuguse, kuid laetud kuulikesega (5) jaotub laeng kahe kuulikese vahel võrdselt.
Coulomb mõõtis kuulikeste vahel mõjuva jõu F ja suurendas kuulikeste vahekaugust kaks korda. Selle tulemusena vähenes jõud neli korda. Nüüd suurendas Coulomb kuulikeste vahekauguse esialgsega võrreldes kolmekordseks ja veendus selles, et jõud oli üheksa korda esialgsest väiksem. Seega vahekaugusel r mõjus laetud kuulikeste vahel jõud F, vahekaugusel 2r jõud F/4, vahekaugusel 3r jõud F/9 jne. Tulemus oli esitatav ka kujul
Nii võis Coulomb teha järelduse, et laetud kehade vahekauguse ruudu ja elektrijõu korrutis on konstantne, teiste sõnadega: laetud kehade vahel mõjuv elektrijõud on pöördvõrdeline kehade vahekauguse ruuduga
Selleks et uurida kuulikeste muutumatu vahekauguse korral jõu sõltuvust laengu suurusest, juhtis Coulomb ühelt vaadeldavalt kuulikeselt laengu ära ning viis kuulikesed uuesti kokkupuutesse. Kui esialgu oli mõlemal kuulikesel laeng q, siis nüüd jäi mõlemale kuulikesele laeng q/2. Kuulikeste vahel mõjuv jõud aga oli sama vahekauguse korral esialgsest neli korda väiksem, seega F/4. Sellise protseduuri kordamisel jäi kuulikestele laeng q/4, jõud aga kahanes väärtuseni F/16. Coulomb mõistis, et kui laeng kahaneb mingi arv kordi, siis jõud kahaneb see arv ruudus kordi. Teisiti öeldes: jõu ja laengu ruudu jagatis on konstantne
Coulomb järeldas, et jõud on võrdeline laengu ruuduga
Teatavasti on mingi arvu ruudu leidmine korrutamise erijuht. Selle põhjal võis Coulomb nüüd väita, et erinevalt laetud kehade vahel mõjuv jõud on võrdeline laengute korrutisega.
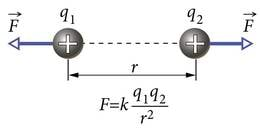
Coulomb jõudis gravitatsiooniseadusega väga sarnase tulemuseni: kahe laetud keha vahel mõjuv elektrijõud on võrdeline kummagi keha laenguga ja pöördvõrdeline kehade vahekauguse ruuduga
kus on võrdetegur. See jõud mõjub laetud kehi ühendava sirge sihis ning sõltub ainest, milles laetud kehad asuvad. Jõud on suurim vaakumis, aga peaaegu niisama suur on ta ka õhus. Jõud on samanimeliste laengute jaoks tõukejõud ja erinimeliste laengute korral tõmbejõud. Jõu mõjumise siht on kehade asukohtadega määratud. Järelikult on jõul kui vektoril vaid kaks võimalikku suunda. Jõu suunda antud sihil võib kirjeldada jõu arvväärtuse ees paikneva märgiga (+ või – ). See omakorda on leitav laengute märkide põhjal. Niisiis tähistab valemis 1.3 ja ka edaspidi jõuvektori pikkust, mis võib olla nii positiivne kui ka negatiivne.
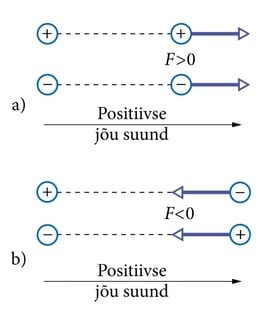
Me vaatleme ühele laetud kehale mõjuvat jõudu positiivsena, kui see on suunatud teisest kehast eemale. Negatiivseks loeme jõudu aga siis, kui see on suunatud teise keha poole. Samanimeliste laengute korrutis on valemis 1.3 alati positiivne. Seega mõjub samanimeliselt laetud kehade vahel positiivne jõud ehk tõukejõud. Erinimeliste laengute korrutis on negatiivne ning kehade vahel mõjub negatiivne jõud ehk tõmbejõud (J.1.8). Sellise kokkuleppega vabaneme vajadusest kasutada jõudu sisaldavates valemites vektorkuju.
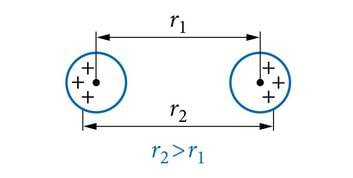
Kõigi Coulomb’i katsete kirjeldustes nimetasime vahekauguseks kuulikeste tsentrite vahelist kaugust. Kui kuulikeste läbimõõt on tühiselt väike võrreldes kuulikeste vahekaugusega, pole selle asjaolu rõhutamine eriti tähtis. Kui aga kuulikeste läbimõõt on vahekaugusele lähedane, siis tuleb vahekauguse mõistet täpsustada. Omavahelise tõukumise tõttu asetuvad samamärgilist laengut kandvad osakesed kummagi kuulikese sellesse ossa, mis jääb teisest kuulikesest võimalikult kaugele (J.1.9). Selle tagajärjel on laengutevaheline kaugus kuulikeste tsentrite vahekaugusest suurem.
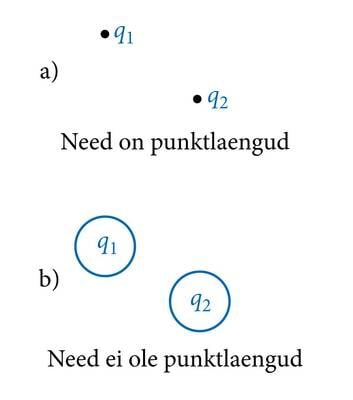
Kuulikeste vahel mõjuv jõud on aga Coulomb’i seaduse põhjal väiksem sellest jõust, millega mõjutaksid teineteist kuulikeste tsentrites paiknevad laengud. Sõna laeng tähendab siin mõistagi laetud osakeste kogumit. Coulomb’i seadus on lühidalt ja täpselt sõnastatav vaid niisuguste laetud kehade jaoks, mille mõõtmed on tühised võrreldes kehade vahekaugusega. Selliseid laetud kehi nimetatakse punktlaenguteks (J.1.10). Punktlaeng mängib elektriõpetuses sama rolli, mis punktmass Mehaanika kursuses. Mistahes keha võib käsitleda punktlaenguna juhul, kui laengu jaotumise keha osade vahel tohib antud ülesandes arvestamata jätta. Keha laengut vaadeldakse siis koondununa ühte punkti. Mingi keha võib ühes ülesandes esineda punktlaenguna, teises aga mitte. Näiteks on laetud veepiisake äikesepilve ja Maa vahel vaadeldav punktlaenguna. Piisa pinna lähedal asuva üksiku iooni jaoks aga laetud veepiisk kindlasti punktlaeng ei ole.
Avaldades valemist 1.3 võrdeteguri , saame
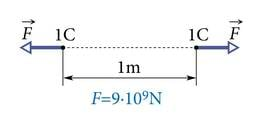
Tegur võrdub arvuliselt jõuga, mis mõjub vaakumis kahe teineteisest 1 m kaugusel paikneva punktlaengu 1 C vahel (J.1.11). Katsetest on kindlaks tehtud, et see jõud oleks 9·109 N ehk niisuguse keha raskusjõud, mille mass on peaaegu miljon tonni. Nii koletule jõule ei suuda vastu panna ükski terastross ega mingi muu ühenduslüli. On ju raske rongi mass “ainult” mõni tuhat tonni ja suure laeva mass ulatub mõnekümne tuhande tonnini. Järelikult on üks kulon väga suur laeng.
Võrdetegur Coulomb’i seaduses on seega vaakumi korral esitatav kujul
Näide 1.2.
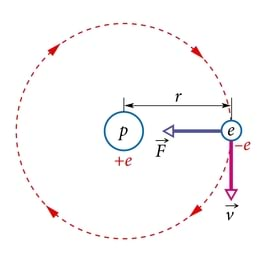
Leiame Coulomb’i seaduse kohaselt elektrijõu , millega ringjoonelisel orbiidil liikuv elektron ja ringjoone tsentris paiknev prooton mõjutavad teineteist vesiniku aatomi planetaarses mudelis (vt joonist). Osakeste vahekauguseks loeme vesiniku aatomi raadiuse, mis Bohri mudeli kohaselt on .
Lahendus
Leiame Coulomb’i seaduse kohaselt elektrijõu , millega ringjoonelisel orbiidil liikuv elektron ja ringjoone tsentris paiknev prooton mõjutavad teineteist vesiniku aatomi planetaarses mudelis (vt joonist). Osakeste vahekauguseks loeme vesiniku aatomi raadiuse, mis Bohri mudeli kohaselt on .
Andmed
Arvutused:
Teame, et
kus
Seega
(miinusmärk näitab, et tegemist on tõmbejõuga). Järelikult
Vastus: Elektroni ja prootoni vahel mõjub elektriline tõmbejõud . Nende osakeste vahel mõjuv gravitatsioonijõud on samas vaid . Seega on elektrijõud vesiniku aatomis gravitatsioonijõust suurem üle korra.
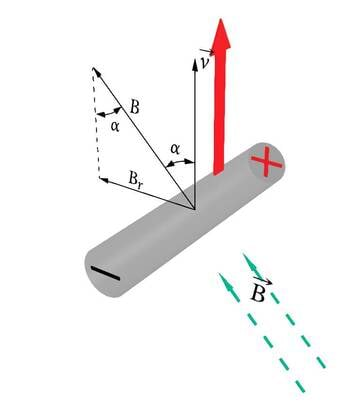
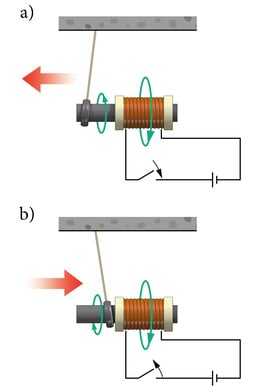
Juba 9. klassi Elektriõpetuses oli juttu sellest, et vooluga juhet ümbritseb magnetväli. Elektrivool on aga laengukandjate suunatud liikumine. Seega tekib laengukandjate suunatud liikumise tulemusena magnetväli.
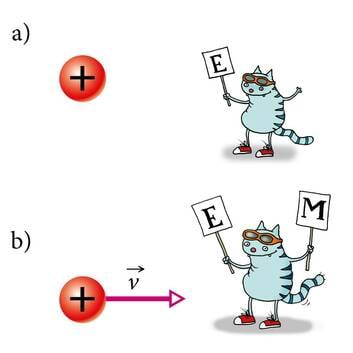
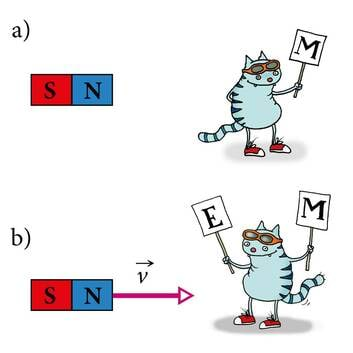
Magnetväljaks nimetatakse laetud osakeste liikumisel tekkivat jõuvälja. Paigalseisev laeng (laetud keha) kutsub esile elektrivälja, liikuv laeng (elektrivool) aga täiendavalt ka magnetvälja. Seega on magnetvälja olemasolu mingi vaatleja jaoks niisama suhteline kui liikumine ise.
Samas pole magnetnähtuste tekkimiseks sugugi alati vaja elektrivoolu. Esmase kogemuse magnetismiga on igaüks meist saanud mitte voolu vaid just püsimagneti magnetvälja kaudu.
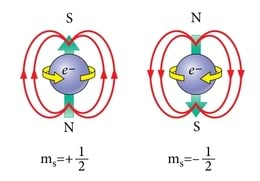
Püsimagnet on olemuslikult magnetvälja omav keha. Selle magnetvälja tekitavad osakesed, millest püsimagnet koosneb. Nii elektron, prooton kui ka neutron tekitavad juba üksnes oma olemasoluga magnetvälja. Seejuures määrab püsimagneti omadused eelkõige elektronide olemuslik magnetväli.
Aineosakese omamagnetväli on seotud osakese sisemise liikumise ehk spinniga. Nimetus tuleneb spinni tõlgendamisest aineosakese pöörlemisena ümber oma telje (ingl.k. to spin - pöörlema). Seda pöörlemist ei saa peatada. Võib vaid muuta pöörlemistelje asendit ruumis. Spinniga kaasneb alati kindel magnetväli, mis on suunatud piki pöörlemistelge. Spinn on osakest sama kindlalt iseloomustav suurus nagu laeng või mass. Seetõttu käsitletakse spinni omalaadse "pöörlemislaenguna". Spinnil puudub lihtne klassikaline mudel, mis kirjeldaks kõiki katsetulemusi. Seetõttu oleme sunnitud leppima üpris ebakonkreetse määratlusega "sisemine liikumine".
Püsimagneti juures võib tinglikult eristada kahte piirkonda, mille mõttelisi keskmeid nimetatakse põhjapooluseks ja lõunapooluseks (tähised vastavalt N ja S). Tähistusviis tuleneb väikese pöördumisvõimelise püsimagneti ehk magnetnõela käitumisest Maa magnetväljas. Nimelt on magnetnõelal kalduvus orienteeruda ehk asetuda ligikaudu piki geograafilist põhja-lõuna suunda.
Orienteerunud magnetnõela seda otsa, mis näitab geograafilist põhjasuunda, on hakatud nimetama magnetnõela või püsimagneti põhjapooluseks ja magnetnõela geograafiliselt lõunapoolset otsa lõunapooluseks.
Magnetnõela kindlaviisiline asetumine magnetväljas määrab magnetvälja kirjeldava vektoriaalse suuruse ehk B-vektori suuna. B-vektorist tuleb lähemalt juttu punktis 1.5.2.
Juba 13. sajandil tehti kindlaks, et ühe püsimagneti põhjapoolus ja teise lõunapoolus tõmbuvad, sama liiki poolused aga tõukuvad. See tulemus oli pöördelise tähtsusega, kuna tavakogemuse kohaselt püsimagnet vaid tõmbab raudesemeid enda poole.
Raudesemete tõmbumist püsimagneti mistahes pooluse suunas põhjustab rauatüki ajutine muutumine magnetiks. Seejuures tekitab püsimagneti üks poolus just rauatüki endapoolses küljes vastupidise magnetpooluse ja kutsub niimoodi esile tõmbejõu. Nähtust, mille korral magnetvälja paigutamise tulemusena hakkab aine ka ise tekitama magnetvälja, nimetatakse aine magneetumiseks.
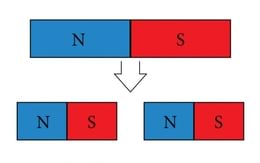
Magnetpooluste uurimisel avastati veel, et püsimagneti poolitamise tulemuseks ei ole mitte kaks lahutatud magnetpoolust, vaid kaks uut püsimagnetit, millel on kummalgi oma põhjapoolus ja oma lõunapoolus (J.1.13). See näitab selgesti pooluste tinglikkust. Järelikult on sarnasus kahe märgiga elektrilaengute ja kahte liiki magnetpooluste vahel vaid näiline. Erimärgilisi elektrilaenguid on ju võimalik ruumis lahku viia, magnetpoolustega seda aga teha ei saa.
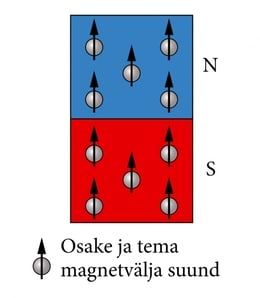
Arvestades, et püsimagneti väli on põhjustatud osakeste omamagnetväljadest, on niisugune tulemus aga kergesti mõistetav. Koosnevad ju kõik püsimagneti piirkonnad ühtedest ja samadest osakestest. Järelikult ei saagi püsimagneti osade vahel põhimõttelist erinevust olla. Magnetpooluste eristamisega kirjeldatakse vaid püsimagneti poolt tekitatava magnetvälja suunda (J.1.14).
Pärast seda, kui Coulomb oli 1785. aastal avastanud elektrijõu pöördvõrdelise sõltuvuse laetud kehade vahekauguse ruudust, asus ta korraldama samalaadseid katseid püsimagnetitega. Coulomb jõudis järeldusele, et ka magnetpooluste vahel mõjuv jõud on pöördvõrdeline poolustevahelise kauguse ruuduga. Niisiis on jõu sõltuvus vastastikmõjus olevate kehade vahelisest kaugusest ühesugune nii elektrijõu kui magnetjõu korral.
| Mitte kõik ained ei käitu magnetväljas ühtmoodi. Pildil näeme ülaltvaates konna, kes hõljub konnast allpool oleva vertikaalse solenoidi voolu poolt tekitatud magnetväljas. | Lihtsalt huvitav fakt: vedelal hapnikul on magnetilised omadused. Täpsemalt, vedel hapnik on paramagneetiline. Mis muuhulgas tähendab seda, et vedel hapnik jääb magneti külge. |
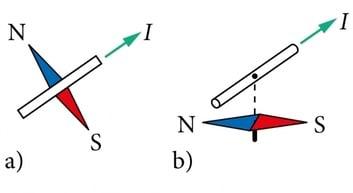
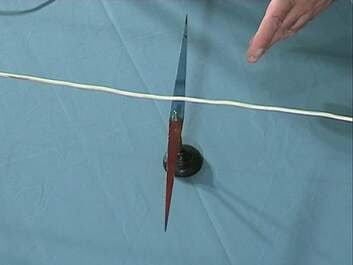
Elektrivoolu magnetvälja uurimise alguseks võib pidada aastat 1820, mil oma töö põhitulemuse avaldas Taani füüsik Hans Christian Oersted. Nimelt avastas Oersted, et juhet läbiv elektrivool avaldab magnetnõelale orienteerivat mõju. Magnetnõel pöördub juhtmega ristuvasse asendisse. Orienteerunud magnetnõel ei ole aga risti mitte ainult juhtme endaga, vaid ka tasandiga, mille määravad juhe ning magnetnõela keskme kinnituspunkt (J.1.15).
See oli tõeliselt üllatav tulemus. Kõik 19. sajandi alguseks tuntud jõud olid ju suunatud piki teineteist mõjutavate kehade keskmeid ühendavat sirget. Seetõttu arvati, et vooluga juhe võiks magnetnõela ühte poolust tõmmata ja teist tõugata. Nagu näeme, on magnetnõelale mõjuvad jõud hoopis risti juhet ja magnetnõela ühendava sirglõiguga.
Oerstedi katse vallandas elektrivoolu magnetvälja uurimisel tõelise laviini. Juba samal 1820. aastal avastasid prantslased Jean-Baptiste Biot [bioo] ja Felix Savart [savaar], et vooluga juhtme mingi lõigu poolt magnetnõela mingile kindlale poolusele mõjuv ja magnetnõela pöörav jõud on võrdeline vaadeldava juhtmelõigu pikkusega ning voolutugevusega juhtmes (J.1.16).
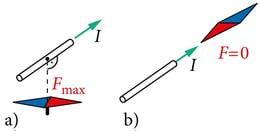
Samas osutus see jõud pöördvõrdeliseks juhtmelõigu ning magnetnõela vahelise kauguse ruuduga, nii nagu Coulomb’i seaduse kohaselt kahe punktlaengu vahel mõjuv jõud. Biot ja Savart leidsid ka, et magnetjõud on tugevaim juhul, kui magnetnõel paikneb vaadeldava juhtmelõigu keskristsirgel. Kui aga magnetnõel asetseb juhtmelõigu pikendusel (juhtmega samal sirgel), siis muutub nõelale mõjuv jõud nulliks (J.1.17). Biot ja Savart mõõtsid magnetjõudu, lastes magnetnõelal võnkuda oma tasakaaluasendi ümber. Mida kiirem (suurema sagedusega) see võnkumine on, seda tugevam on tasakaaluasendi poole suunatud magnetjõud. Täpsemalt öeldes on magnetjõud võrdeline magnetnõela võnkesageduse ruuduga.
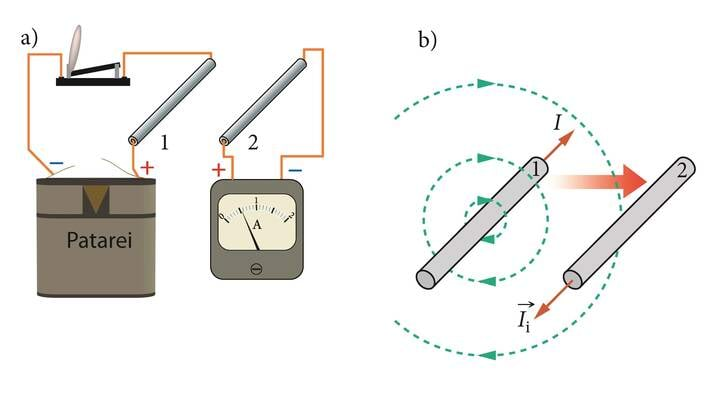
Lähtudes teadmisest, et elektrivool on suuteline mõjutama püsimagnetit, on loomulik küsida, kas ka kaks vooluga juhet teineteist magnetjõuga mõjutavad. Veel samal 1820. aastal näitas André Marie Ampère, et see on tõesti nii. Ampère tuli esimesena mõttele, et magnetvälja tekitab laengukandjate liikumine. Enne teda püüti voolu magnetvälja taandada püsimagneti väljale. Nimelt arvati, et voolu tekitamine juhtmes muudab juhtme mingil viisil püsimagnetiks. Ampère aga esitas julgelt vastupidise hüpoteesi: just püsimagneti väli on põhjustatud tema sees kulgevatest ringvooludest. Hiljem selgus, et Ampère’il oli selles ka üksjagu õigus. Mõnede ainete magnetilised omadused on tõesti määratud neis moodustunud vooluringide magnetväljaga.
Ampère uuris kõigepealt kahe juhtme vastastikmõju juhtmete muutumatu pikkuse ja vahekauguse korral ning avastas järgmised seaduspärasused:
- Kui kaks juhtmelõiku paiknevad erinevates tasandites, kuid risti nende keskpunkte ühendava lõiguga, kusjuures paiknemistasandi määravad kummagi juhtme jaoks juhe ise ja ühenduslõik, siis juhtmelõikude vahel mõjuv jõud sõltub nurgast nende vahel. Paralleelsete juhtmete korral on jõud maksimaalne. Ristuvate juhtmete keskmete vahel jõudu ei mõju.
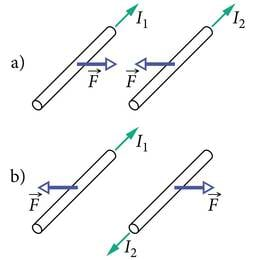
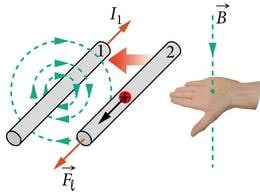
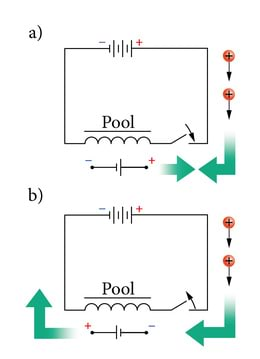
- Kui paralleelsetes juhtmetes kulgevad samasuunalised voolud, siis mõjub juhtmete vahel tõmbejõud. Vastassuunaliste voolude korral mõjub tõukejõud (J.1.18).
- Jõud on alati risti juhtmelõiguga, millele ta mõjub.
Seega on voolude vastastikmõju mingis mõttes vastupidine laengute vastastikmõjule. Teatavasti mõjub samanimeliste laengute vahel tõukejõud, samasuunaliste voolude vahel aga tõmbejõud. Vastandmärgilised laengud tõmbuvad teineteise poole, vastandlike suundadega voolud aga tõukuvad teineteisest eemale. Järgnevalt asus Ampère välja selgitama paralleelsete sirgjuhtmete vastastikmõju sõltuvust nende pikkusest ja vahekaugusest. Ta tegi kindlaks, et juhtmete vahel mõjuv magnetjõud on võrdeline voolutugevustega ja kummaski juhtmes ning vaadeldava juhtmeosa pikkusega . Samas osutus see jõud pöördvõrdeliseks juhtmete vahekaugusega . Katsete tulemused võis Ampère kokku võtta valemisse
milles sisalduv konstant sõltub üldjuhul ainest, kus juhtmed asuvad.
Ampère’i seaduse (valem 1.7 ) kaudu on määratud voolutugevuse ühik amper (1 A).
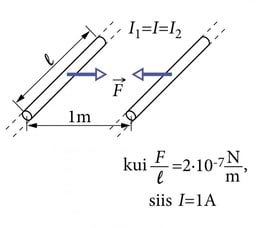
Kui kahe paralleelse, lõpmata pika ja lõpmata peenikese sirgjuhtme vahel, mille vahekaugus on üks meeter ja milles voolab ühesuguse tugevusega vool, mõjub vaakumis juhtmete pikkuse iga meetri kohta jõud 2·10–7 njuutonit, siis on voolutugevus juhtmetes üks amper (J.1.19). Valemis 4.1 sisalduva konstandi väärtus on vaakumi korral seega 2·10–7 N/A2.
Lõpmata pikki ja peenikesi juhtmeid tegelikkuses mõistagi olemas ei ole. Seetõttu loetakse ampri etalonkatse teostatuks seda paremini, mida suurem on juhtmete vahekaugus võrreldes nende läbimõõduga ning mida pikemad on omakorda juhtmed võrreldes nende vahekaugusega. Amper on SI elektriliseks põhiühikuks. Selle kaudu tuletatakse kõigi teiste elektriliste suuruste mõõtühikud. Samas on ampri definitsioon niivõrd pikk, et lõppu välja jõudes kipub algus juba meelest minema. Seepärast ei tasuks seda mitte luuletuse kombel pähe õppida, vaid püüda silme ees hoida joonist 1.19.
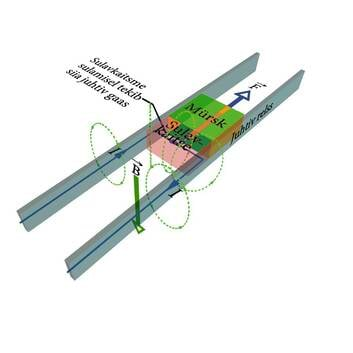
| Relsskahur selles tekitatud vooluga i. See vool põhjustab sulavkaitsme kiire aurustumise. Vool tekitab relsside vahel magnetvälja B ja see magnetväli rakendab jõudu F juhtivale gaasile, mis on osa voolu kulgemisteest. Gaas lükkab mürsku piki relsse ja lennutab selle minema. | Relsskahuri mürsk lendab ... miks on sellel taga "tulesaba", ehkki midagi selle mürsu juures ei põle? |
Näide 1.3
Lahendus
Andmed
Arvutused
Valemist 1.7 teame, et
Järelikult
Püsimagneti poolused
Püsimagneti juures eristatakse tinglikult kahte piirkonda, mille mõttelisi keskmeid nimetatakse põhjapooluseks ja lõunapooluseks. Erinimeliste magnetpooluste vahel mõjub tõmbejõud, samanimeliste pooluste vahel aga tõukejõud.
Paralleelsete juhtmete vahel mõjuva jõu suund.
Kui paralleelsetes juhtmetes kulgevad samasuunalised voolud, siis mõjub juhtmete vahel tõmbejõud. Vastassuunaliste voolude korral mõjub tõukejõud.
Paralleelsete juhtmete vahel mõjuva jõu suurus
Kahe paralleelse sirgjuhtme vahel mõjuv jõud on võrdeline juhtmete pikkusega ning voolutugevustega juhtmetes. See jõud on ka pöördvõrdeline juhtmete vahelise kaugusega. Võrdeteguri väärtus on vaakumi korral 2·10–7
Aine ja tema olekute kirjeldamiseks kasutatakse mitmesuguseid füüsikalisi suurusi, millest mõned on meile ka juba põhikoolist tuttavad. Välja võib samuti kirjeldada mingi suuruse abil. Kuna välja olemasolu tuleb esile jõu kaudu, siis on mõistlik elektri- ja magnetvälja iseloomustada jõuga, mis mõjub selles väljas mingile kindlale kehale.
Jõud , millega ühe punktlaengu poolt tekitatav elektriväli mõjutab teist punktlaengut , sõltub Coulomb’i seaduse (valemi 1.3 )
kohaselt mõlema laengu suurusest. Seega ei sobi jõud kirjeldama elektrivälja, mida tekitab esimene punktlaeng . Elektrivälja iseloomustava suuruse väärtused ei tohi ju sõltuda vahendist (proovikehast laenguga ), mida me kasutame välja olemasolu tuvastamiseks. Kui me jagame proovikehale mõjuva jõu selle keha laenguga , siis saame suuruse, mis tõepoolest ei sõltu enam laengust . See ongi esimese keha poolt tekitatava elektrivälja tugevus
Elektrivälja tugevus näitab, kui suur jõud mõjub selles väljas ühikulise positiivse laenguga kehale. Väljatugevus on vektoriaalne (suunda omav) suurus. Seetõttu võib väljatugevust lühidalt nimetada ka E-vektoriks. Edaspidi teeme nii eelkõige siis, kui soovime rõhutada väljatugevuse vektoriaalsust. Kui aga jutt on E-vektori pikkusest (moodulist), siis ütleme lihtsalt väljatugevus . Topeltindeksiga jõu tähises rõhutame, et tegemist on jõuga, mis mõjub esimese keha poolt teisele kehale.
E-vektori kokkuleppelise suuna määrab elektrivälja tugevuse definitsioonis sisalduv sõna positiivne. Kuna kahe positiivselt laetud keha vahel mõjub tõukejõud, siis on positiivse laenguga keha poolt tekitatud elektrivälja tugevus vektorina suunatud sellest kehast eemale. Me võiksime valemis 1.10 kasutada vektorimärke, sest proovikeha laengu positiivsuse tõttu on jõud ja väljatugevus vektoritena samasuunalised. Negatiivse laenguga keha mõjutab positiivset proovilaengut tõmbejõuga, mistõttu vastav elektrivälja tugevus on vektorina suunatud negatiivse laenguga keha poole.
Üldiselt tuleb vektoriaalsete suuruste tähiseid käesoleva õpiku valemites siiski mõista kui vastavate vektorite pikkusi. Pikkuse negatiivsus tähendab aga seda, et vektor on suunatud vastupidiselt kokkuleppelisele positiivsele suunale. Näiteks on jõud ja väljatugevus negatiivse laenguga väljatekitaja korral valemis 1.10 mõlemad negatiivsed. Valemite lihtsuse nimel hoidume vektorimärkide kasutamisest.
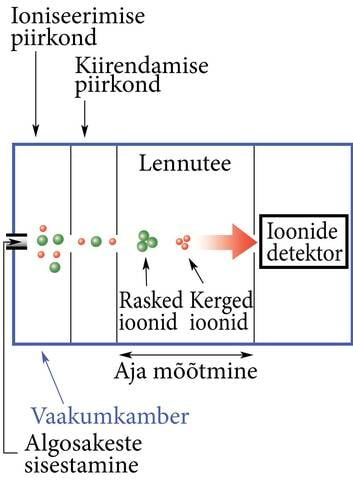
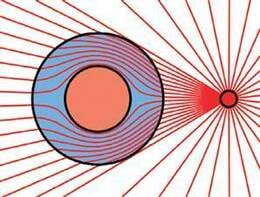
| Osakeste lennuaega mõõtvate mass-spektromeetrite töö põhineb elektrivälja mõjul laenguga kehale. Siin erineva massiga, aga ühesuguse laenguga ioonid läbivad homogeense elektrivälja (vt punkt 1.6.2) piirkonna ja saavad seal tänu oma erinevatele massidele erineva kiirenduse. Osakeste lennuaegasid mõõtes saab siis teada, missuguse massiga ioone uuritavas gaasis leidub. | Ka õhus tekkivad sädemed annavad märku tugeva elektrivälja olemasolust |
Valemi 1.10 põhjal on elektrivälja tugevuse ühikuks üks njuuton kuloni kohta (). Üks njuuton kuloni kohta on sellise elektrivälja tugevus, milles punktlaengule suurusega mõjub jõud . Praktikas see esitus eriti kasutamist ei leia. Rohkem on levinud sama mõõtühiku teine esitusviis - üks volt meetri kohta (). Sellega tutvume lähemalt punktis 1.6.
Elektrivälja tugevuse kohta toodud mõned näited tabelis 1.2.
|
Väli |
Väljatugevus |
|
põleva elektrilambi hõõgniidis |
400 – 600 |
|
õhus vahetult enne välgulööki |
kuni 5·105 |
|
sädeme tekkimisel kuivas õhus (sõltub sädeme pikkusest) |
3·106 |
|
elusa raku membraanis |
2·107 |
|
vesiniku aatomissse kuuluva elektroni asukohas |
5·1011 |
Edaspidi tuleb meil korduvalt väljatugevuse kaudu leida kehale laenguga selles väljas mõjuvat elektrijõudu . Valemi 1.10 põhjal
jõud on laengu ja väljatugevuse korrutis. Indekseid me enam ei kasuta, sest valemis 1.11 sisalduv väljatugevus ei pruugi enam olla põhjustatud konkreetsest punktlaengust ega üldse mingist ühest kindlast kehast. See on enamasti paljude eri väljade tugevuste summa.
Eespool veendusime selles, et laeng täidab Coulomb’i seaduses sama rolli mida mass gravitatsiooniseaduses. Võrdlemist jätkates võiksime küsida, milline Mehaanika kursusest tuntud suurus vastab elektrivälja tugevusele . Pole kuigi raske märgata, et selleks suuruseks on raskuskiirendus . Raskuskiirendus näitab, kui suur raskusjõud mõjub ühikulise massiga kehale. Analoogiliselt näitab elektrivälja tugevus meile, kui suur elektrijõud mõjub selles väljas ühikulise laenguga kehale.
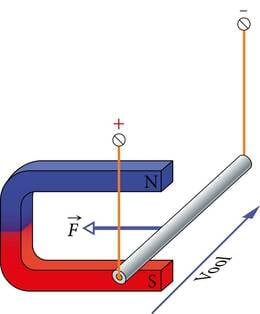
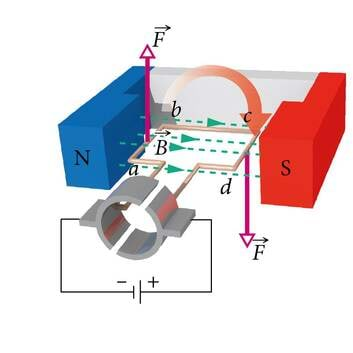
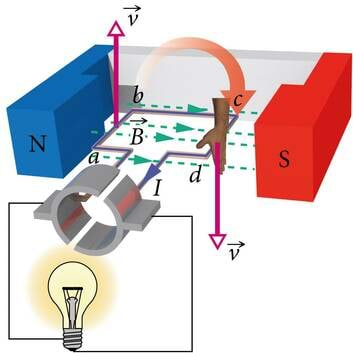
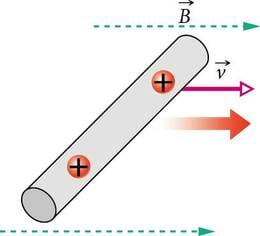
Kui uurime katseliselt vooluga juhtme käitumist mitte ainult teise juhtme magnetväljas (p.1.4.2) vaid suvalise päritoluga väljas, siis võime järeldada, et juhtmelõigule mõjuv magnetjõud on alati võrdeline juhet läbiva voolu tugevusega , juhtmelõigu pikkusega ja siinusega nurgast voolu suuna ning magnetvälja suuna vahel (J.1.20)
kus on võrdetegur. Meenutagem siinkohal, et magnetvälja suuna määrab selles väljas orienteerunud magnetnõel. Peagi veendume, et seos 1.12 on Ampère’i poolt tuletatud valemi 1.7 üldistus, mis arvestab ka magnetvälja suunda ja ei eelda enam magnetvälja tekitajana vooluga juhet. Seetõttu nimetatakse valemit 1.12 sageli Ampère’i seaduseks, ehkki Ampère ise kasutas kuju 1.7 .
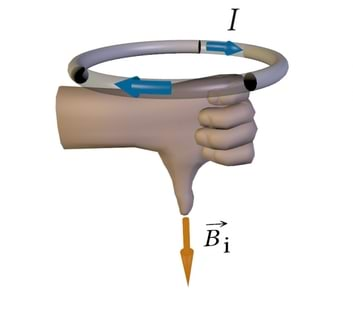
Jõu suuna määramiseks Ampère’i seaduses võib kasutada vasaku käe reeglit. See väidab, et kui vasaku käe väljasirutatud sõrmed osutavad voolu suunda ja magnetväli on suunatud peopessa, siis väljasirutatud pöial näitab juhtmelõigule mõjuva jõu suunda (J.1.20). Vooluga juhtmele mõjuv magnetjõud on suunatud alati risti nii voolu kui ka magnetvälja suunaga. Nüüd märkame, et meil on mõtet avaldada valemist 1.12 võrdetegur , tehes seda juhul, kui magnetväli on voolu suunaga risti ( ja ). Me saame, et
suurus näitab uuritavas magnetväljas mingile kindlale kehale (vooluga juhtmele) mõjuvat jõudu. Seega on ta sobiv kasutamiseks magnetvälja iseloomustava suurusena. Suurust on hakatud nimetama magnetinduktsiooniks.
Magnetinduktsioon näitab magnetjõudu , mis mõjub ühikulise vooluga ja ühikulise pikkusega juhtmelõigule selle juhtmega ristuvas magnetväljas.
Magnetinduktsioon on vektoriaalne suurus ja tema suunda näitab magnetväljas orienteerunud magnetnõela põhjapoolus (J.1.20).
Kuna magnetinduktsiooni üldlevinud tähiseks on , siis võib teda lühidalt nimetada ka B-vektoriks. Pole raske märgata, et B-vektor on analoogiline elektrivälja kirjeldava E-vektoriga. Mõlemad on defineeritud jõu kaudu, mis mõjub proovikehale. Erinevus on vaid selles, et E-vektori suund ühtib laetud proovikehale mõjuva jõu mõjumise sihiga, B-vektor on aga proovijuhtmele mõjuva jõu suunaga risti. Viimane asjaolu muudab täiesti võimatuks vektorimärkide kasutamise valemites 1.12 ja 1.13 . Allpool (p.1.5.4) saab ka selgemaks, miks B-vektori pikkuse defineerimisel kasutatakse vooluga juhet, suuna määramisel aga püsimagnetit.
Magnetinduktsiooni SI-ühikut nimetatakse horvaadi päritoluga Ameerika elektrotehniku ja leiutaja Nikola Tesla (1856 – 1943) järgi teslaks. Kui juhtmele, mille pikkus on üks meeter ja milles kulgeb vool tugevusega üks amper, mõjub selle juhtmega ristuva magnetvälja poolt jõud üks njuuton, siis on välja magnetinduktsioon üks tesla (1 T) (J.1.21).
Seega valemi 1.13 kohaselt
Üks tesla on väga suur magnetinduktsioon. Seetõttu mõõdetakse Maal esinevate magnetväljade induktsioone tavaliselt milli- ja mikroteslades. Keskmise suurusega püsimagneti pinna lähedal on magnetinduktsioon mõnikümmend milliteslat. Tabelis 1.3 on toodud veel mõned näited magnetinduktsiooni väärtuste kohta.
Coulomb’i seaduse 1.3 ja valemi 1.10 abil saame punktlaengu elektrostaatilise välja tugevuse esitada kujul
Seega on punktlaengu väljatugevus võrdeline selle laengu suurusega ning pöördvõrdeline laengu ja uuritava punkti vahekauguse ruuduga.
Teades Oerstedi katse kirjelduse (p.1.4.2) põhjal seda, kuidas on suunatud sirgvoolu magnetväli, võime nüüd omavahel seostada Ampère’i seaduse kaks kuju (1.7 ja 1.12) ning ühtlasi avaldada vooluga sirgjuhtme poolt tekitatava magnetinduktsiooni. Kahe paralleelse juhtme korral on ühe juhtme magnetväli teise juhtmega risti (J.1.22).
Seega nurk on täisnurk ja . Vastavalt avaldub esimese juhtme poolt teisele mõjuv jõud kujul
kus on esimese juhtme magnetinduktsioon teise juhtme asukohas ja on voolutugevus teises juhtmes. Kuna jõud avaldub samas ka valemiga 1.7
siis saame
Vooluga sirgjuhtme poolt tekitatav magnetinduktsioon on võrdeline voolutugevusega juhtmes ning pöördvõrdeline kaugusega juhtmest. Valemi 1.15 juures tuleb arvestada, et on selle juhtmelõigu pikkus, millele vaadeldav jõud mõjub. Vaikimisi eeldatakse magnetinduktsiooni tekitava (joonisel vasakpoolse) juhtme lõpmatut pikkust.
Näide 1.4.
Leiame magnetinduktsiooni, mida tekitab näites 1.3 käsitletud õhuliini üks juhe teise asukohas. Juhtmete vahekaugus on ja neis kulgeb vool TeX parse error: Undefined control sequence \textA.
Lahendus
Andmed
Arvutused
Valem 1.15 annab
kus
Arvutades saame
Vastus: Üks juhe tekitab teise asukohas magnetinduktsiooni 20 mikroteslat.
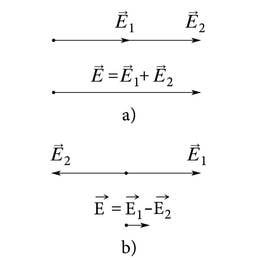
Nii elektri- kui magnetväljas kehtib superpositsiooniprintsiip ehk liitumise põhimõte. Selle printsiibi kohaselt võrdub elektrivälja korral laetud kehade süsteemi väljatugevus üksikutest kehadest põhjustatud väljatugevuste vektoriaalse summaga. Magnetväljas võrdub väljatekitajate (püsimagnetite või vooluga juhtmete) süsteemi magnetinduktsioon üksikutest väljatekitajatest põhjustatud magnetinduktsioonide vektoriaalse summaga. Veel lihtsamalt öeldes: nii E-vektoreid kui B-vektoreid tuleb vektoriaalselt liita.
Superpositsiooniprintsiip tuleneb otseselt välja omadusest mitte segada teist välja ehk siis Füüsikalise looduskäsitluse aluste kursuses vaadeldud tõrjutusprintsiibist. Täpsemalt tuleneb see küll tõrjutusprintsiibi mittekehtivusest väljade korral. Kui mingile kehale mõjub korraga mitu välja, siis liituvad vektoriaalselt nendest väljadest tingitud jõud. Piltlikult öeldes: väljad ei lähe omavahel konflikti. Nad jagavad omavahel ära võimaluse vaadeldavat keha jõuga mõjutada. Lõpptulemuses kajastub aga loomulikult rohkem selle välja mõju, mis ise on tugevam. Konkreetselt uurime superpositsiooniprintsiibi rakendamist punktis 1.6.
Elektri- ja magnetvälja kirjeldused tunduvad esmapilgul üksjagu erinevat. E-vektori suund ühtib laetud proovikehale mõjuva jõu mõjumise sihiga, B-vektor on aga proovijuhtmele mõjuva jõu suunaga risti. Punktlaengu elektrivälja tugevus (E-vektori pikkus) on pöördvõrdeline vahekauguse ruuduga välja tekitava punktlaengu ja uuritava väljapunkti vahel (valem 1.14). Lõpmata pika sirgjuhtme magnetinduktsioon (B-vektori pikkus) on aga pöördvõrdeline selle kaugusega esimeses astmes (valem 1.15). Need erinevused tulenevad looduse objektiivsest omadusest. Magnetväljal lihtsalt on kaks erinevat tekitajat: laetud osakeste suunatud liikumine (elektrivool) ja osakeste omamagnetväli, mis põhjustab püsimagneti välja. Kui magnetvälja kirjeldav suurus oleks defineeritud lähtuvalt vaid ühest välja tekitajast, siis oleks teise tekitajaga seotud nähtuste kirjeldamine ääretult raske. Seetõttu on tänapäeval B-vektori pikkus määratud vooluga juhtme, suund aga püsimagneti (magnetnõela) abil.
Magnetvälja algne kirjeldus ehitati üles sarnasusele punktlaengute ja magnetpooluste käitumise vahel. Magnetismi tehnilised rakendused aga osutusid üha rohkem seotuks elektrivooluga, mistõttu elektriliseks põhiühikuks valiti amper ja B-vektori pikkus defineeriti süsteemis SI vooluga juhtmele mõjuva jõu kaudu. See tingis magnetvälja silindrilise sümmeetria: kõigis vooluga juhtmest (kui silindri teljest) ühesugusel kaugusel paiknevates punktides on sama magnetinduktsioon. Seevastu punktlaengu elektrivälja sümmeetria on sfääriline: kõigis punktlaengust (kui sfääri tsentrist) ühesugusel kaugusel asuvates punktides on sama elektrivälja tugevus. Sfääri pindala () on võrdeline raadiuse ruuduga, silindri külgpindala () on aga võrdeline raadiusega esimeses astmes.
Elektri- ja magnetvälja võrdlev tabelHomogeenset välja ning elektri- ja magnetvälja jõujooni uurime lähemalt allpool (p.1.6). Olgu veel märgitud, et suur kõlaline erinevus välja jõu kaudu kirjeldavate vektorsuuruste nimetustes (elektrivälja tugevus E ja magnetinduktsioon B) tuleneb samuti asjaolust, et magnetvälja algne kirjeldus ehitati üles sarnasusele punktlaengute ja magnetpooluste käitumise vahel. Magnetvälja tugevuseks nimetatakse suurust, mis on elektrivälja tugevuse analoogiks magnetpooluste-põhises magnetvälja käsitluses. Kuna see käsitlus ei ole kooskõlas tänapäeval domineeriva ühikusüsteemiga SI, siis me seda lähemalt ei vaatle.
Elektrivälja tugevuse suund
Elektrivälja tugevus on vektoriaalne suurus ja seda võib nimetada ka E-vektoriks. E-vektori suund ühtib positiivse laenguga kehale mõjuva jõu suunaga.
Vasaku käe reegel
Kui vasaku käe väljasirutatud sõrmed osutavad voolu suunda ja magnetväli on suunatud peopessa, siis väljasirutatud pöial näitab juhtmelõigule mõjuva jõu suunda (vasaku käe reegel).
Magnetinduktsiooni suund
Magnetinduktsioon on vektoriaalne suurus ja seda võib nimetada ka B-vektoriks. B-vektori suunda näitab magnetväljas orienteerunud magnetnõela põhjapoolus.
Elektri- ja magnetväli pole meie meeleorganitega vahetult tajutavad. Välja olemasolu avaldub vaid tema mõjus aine osakestele. Samas võib aga korraldada katseid, milles väikesed ainekübemed moodustavad E- või B-vektoriga paralleelseid jooni. Neid jooni on hakatud nimetama vastava vektori joonteks või vastava välja jõujoonteks. Jõujooned võimaldavad meil tekitada vahetult nähtavaid välja mudeleid. Teisisõnu – nad võimaldavad elektri- või magnetvälja visualiseerida. Ei tohi unustada, et jõujooni looduses tegelikult pole. Nad on vaid inimeste poolt välja mõeldud abivahend välja kirjeldamisel. Magnetvälja jõujoontest oli juttu juba põhikooli Elektriõpetuses, kuna nende katseline uurimine on tehniliselt hulga lihtsam. Meie aga alustame elektrivälja jõujoontest.
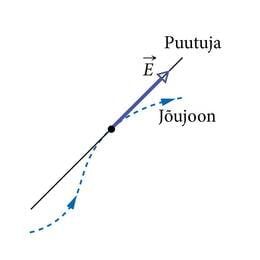
Elektrivälja jõujoon on mõtteline joon, mille igas punktis on E-vektor suunatud piki selle joone puutujat. E-vektori suund määrab ka jõujoone suuna, mida markeeritakse noolekesega jõujoonel (J.1.23). Jõujoone üldlevinud tähiseks joonistel ongi noolekesega katkendjoon, mille läheduses paikneb viide konkreetse välja vektorile (täht E või B). Seal, kus väli on tugevam, paiknevad jõujooned tihedamalt. See võimaldab võrrelda väljatugevusi ruumi eri osades.
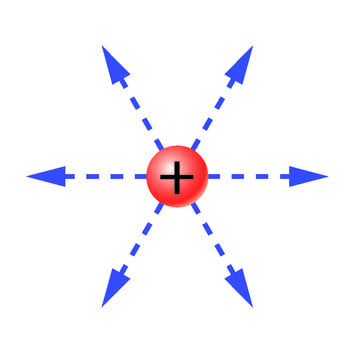
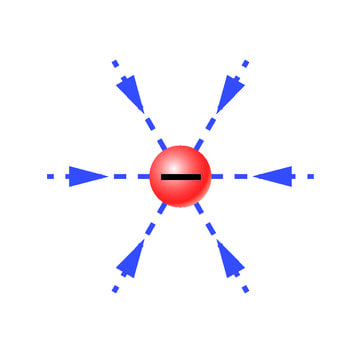
Kui punktlaengu läheduses ei leidu teisi laetud kehi, siis täidab seda ruumi vaid punktlaengu enda elektriväli. Positiivse punktlaengu E-vektor on suunatud laengust eemale ja negatiivse punktlaengu E-vektor laengu poole (J.1.24). Niisiis väljuvad positiivse punktlaengu elektrivälja jõujooned laengu asukohast nagu päikesekiired. Negatiivse punktlaengu välja jõujooned aga tulevad laengu asukohta kokku.
Sageli väidetakse, et positiivselt laetud keha elektrivälja jõujooned lähevad kehalt lõpmatusse ning negatiivse laenguga keha välja jõujooned tulevad lõpmatusest. Päris nii see siiski ei ole. Laengu jäävuse seaduse (p.1.2.4) põhjal teame, et kui on olemas positiivne, siis peab kuskil olema ka negatiivne laeng. Positiivse laenguga kehalt väljuvad elektrivälja jõujooned kulgevad kindlasti mingitele negatiivsetele laengutele. Kui negatiivse laenguga kehad on väga kaugel, siis nende olemasolu positiivselt laetud keha läheduses tunda ei ole ning punktlaengu elektrivälja jõujoonte pilt on tsentraalsümmeetriline.
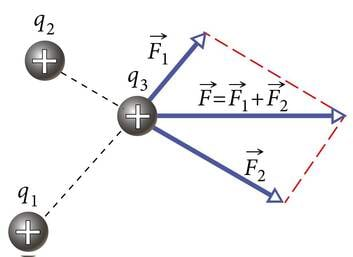
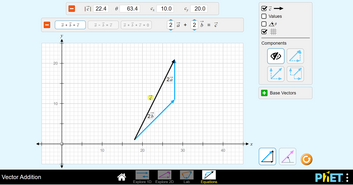
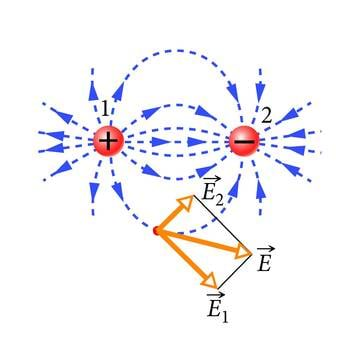
Kahe või enama punktlaengu või muu laetud keha piisavalt väikese vahekauguse korral liituvad superpositsiooniprintsiibi kohaselt nende kehade poolt tekitatud elektriväljade E-vektorid. Summaarse elektrivälja ehk resultantvälja E-vektori leidmise näitena vaatleme kahest ühesuurusest, kuid erinimelisest punktlaengust koosnevat süsteemi (J.1.25). Positiivse punktlaengu väljatugevus on joonisel negatiivse laengu väljatugevusest suurem seetõttu, et vaadeldav punkt paikneb laengule lähemal kui laengule . Liites analoogiliselt E-vektoreid teistes punktides, saame resultantvälja jõujoonte täieliku pildi. Näiteid erinevate kehade ja nende süsteemide elektrivälja jõujoonte konstrueerimisest võib leida veebiõpikust.
Neid elektrivälja jõujoonte pilte saab ka katseliselt kontrollida, kasutades tahke aine kübemeid, mis paiknevad vedelas dielektrikus. Suurepäraselt sobivad selleks mannaterad õlis. Mannaterad asetuvad elektriväljas piki jõujooni ridadesse.
Veelgi lihtsam võimalus erinevaid situatsioone läbi mängida on arvutisimulatsioonid.
Eemaldumisel punktlaengust väheneb punktlaengu väljatugevus valemi 1.14 kohaselt niisamuti nagu kooskõlas Mehaanika kursuses õpituga väheneb raskuskiirendus eemaldumisel Maast. Maapinnal asetsevad kehad on aga kõik ligikaudu ühesugusel kaugusel Maa keskpunktist. Seetõttu võib raskuskiirenduse väärtust Maa pinnal lugeda konstantseks. Jättes Maa pinna kõveruse arvestamata, võime lugeda muutumatuks ka raskuskiirenduse suuna. Raskusjõu välja nimetatakse sel juhul homogeenseks (kr homogenes - ühtlane, ühesugune).
Ka elektriväli võib olla homogeenne. Homogeense välja E-vektor on kogu vaadeldavas ruumis ühesuguse pikkuse ja suunaga ning välja jõujooned on omavahel paralleelsed sirged, mille vahekaugus ei muutu.
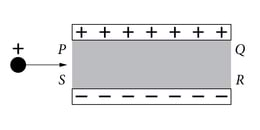
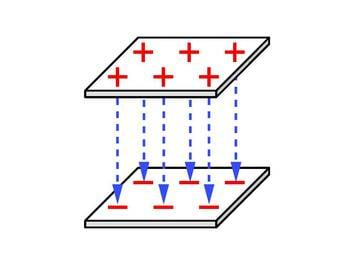
Elektriväli on homogeenne näiteks kahe paralleelse ühtlaselt laetud tasase plaadi vahel, mille pinnaühikul paiknevad suuruselt võrdsed ja vastandmärgilised laengud, plaatide vahekaugus on tühiselt väike võrreldes plaatide joonmõõtmetega ja uuritav piirkond asub piisavalt kaugel plaadi äärest (ääre mõju ei avaldu, J.1.27). Selline elektriväli tekib plaatkondensaatoris, millega tutvume lähemalt allpool (p.2.6.3). Katseline elektrivälja jõujoonte pilt kondensaatoris on joonisel 1.28 (selle saamist kirjeldav video on leitav veebiõpikust). Plaatkondensaatoris tekkivat elektrivälja tasub detailsemalt uurida põhjusel, et kondensaator on üks tähtsamatest elektrostaatika rakendustest.
Mannateradest moodustuvate ridade omavaheline paralleelsus ja ridade keskeltläbi konstantne vahekaugus näitavad, et elektriväli kahe ühtlaselt laetud plaadi vahel on homogeenne. Samas näeme ka, et väljaspool plaatidevahelist ruumi mannaterade reastumist ei toimu. Seega puudub seal elektriväli. Kui ühe plaadi mingil pinnaosal paikneva positiivse laengu jaoks asetseb sama suur negatiivne laeng vahetus läheduses naaberplaadi sama suurel pinnaosal, siis moodustavad need kaks laengut tervikuna neutraalse süsteemi, mis süsteemist väljapoole ulatuvat elektrivälja ei tekita. Piltlikult öeldes: iga pluss on juba “oma” miinuse leidnud ja “lisa otsida” pole enam vaja. “Miinuse otsimist” ehk positiivse laengu ülehulka süsteemis väljendaks selles näites süsteemist väljapoole suunduv jõujoon, mida me aga katses ei tuvasta.
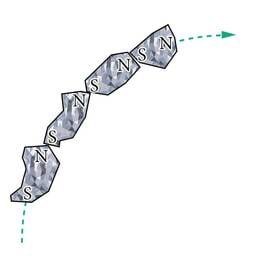
Analoogiliselt elektrivälja jõujoontega kasutatakse ka magnetvälja kirjeldamiseks jõujooni. Magnetvälja jõujoon on mõtteline joon, mille igas punktis on B-vektor suunatud piki selle joone puutujat (analoogiliselt joonisega 1.23). Jõujoonel on ka suund, mis ühtib B-vektori suunaga antud punktis ja mida järelikult näitab orienteerunud magnetnõela põhjapoolus. Seega on võimalik magnetvälja jõujoonte kuju uurida piisavalt suure hulga magnetnõelte abil. Veel paremini saab jõujoonte paigutust nähtavaks muuta rauapuruga. Rauapuru kübemed käituvad magnetväljas nagu väikesed magnetnõelad. Nad pöörduvad oma pikima mõõtmega magnetvälja suunas, üritades püsimagnetite kombel moodustada ahelaid, milles ühe tükikese põhjapoolus on tõmbunud vastu teise lõunapoolust (J.1.29). Sellised ahelad kujutavadki magnetvälja jõujooni.
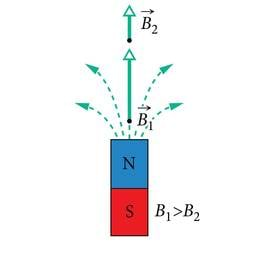
Ka magnetvälja korral võimaldavad jõujooned võrdlevalt hinnata väljavektori pikkust ruumi eri piirkondades. Seal, kus jõujooned paiknevad tihedamalt, näiteks püsimagneti ühe pooluse läheduses (J.1.30), on magnetinduktsioon suurem ja proovikehale mõjuvad tugevamad magnetjõud.
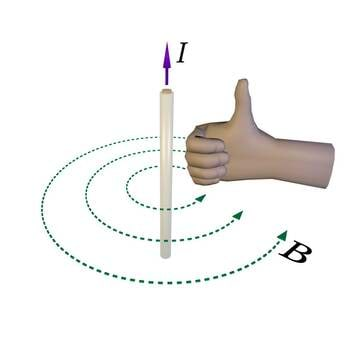
Korraldades Oerstedi katse (p.1.4.2) vertikaalse sirgjuhtme abil, millest ühesugusel kaugusel horisontaalsel alusplaadil paikneb suur hulk magnetnõelu, võime veenduda selles, et magnetvälja jõujooned ümbritsevad vooluga juhet kontsentriliste ringjoontena. Välja suuna määramiseks jõujoonel kasutatakse mitmeid mnemotehnilisi võtteid, millest levinuimaks on tänapäeval parema käe rusikareegel (J.1.31). See väidab, et kui rusikasse tõmmatud parema käe väljasirutatud pöial näitab voolu suunda, siis neli kõverdatud sõrme näitavad selle voolu magnetvälja suunda.
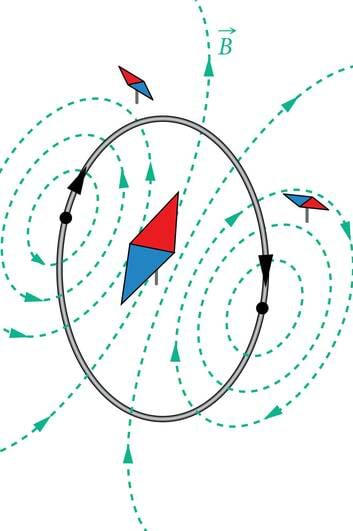
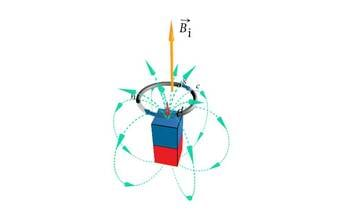
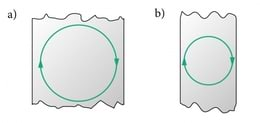
Ka magnetinduktsiooni kohta kehtib superpositsiooniprintsiip ehk liitumise põhimõte. Selle järgi on kehade süsteemi poolt tekitatud magnetvälja B-vektor võrdne üksikute kehade B-vektorite summaga. Ehk teisiti: erinevate kehade poolt mingis punktis tekitatud magnetväljade B-vektoreid tuleb resultantvälja B-vektori saamiseks liita. Seda põhimõtet illustreerib hästi ringvoolu magnetvälja jõujoonte määramine (J.1.32).
Parema käe rusikareeglit rakendades veendume selles, et vooluga ringjuhtme kõik osad tekitavad ringi keskpunktis piki ringjuhtme telge suunatud magnetvälju. Ringjuhtme teljel on resultantväli just ringvoolu keskpunktis kõige tugevam, sest keskpunkt on kõigile ringjuhtme osadele lähim telje punkt ning just keskpunktis on kõigi ringjuhtme osade magnetväljad omavahel paralleelsed. Näeme, et ringvoolu magnetvälja jõujooned ei ole ise küll rangelt ringjoonelised, kuid nad on siiski kinnised kõverad.
Ringvoolu magnetvälja suuna määramiseks võib samuti kasutada parema käe rusikareeglit, mis nüüd kõlab järgmiselt: kui rusikasse tõmmatud parema käe neli kõverdatud sõrme näitavad ringvoolu suunda mingis juhtmekeerus, siis väljasirutatud pöial näitab selle voolu magnetvälja suunda juhtmekeeru teljel. Seega tuleb üleminekul sirgvoolu magnetvälja juurest ringvoolu magnetvälja käsitlemisele parema käe rusikareeglis sõnad vool ja magnetväli omavahel ära vahetada. Ringjuhtme magnetvälja jõujoonte katseline pilt on leitav veebiõpikust.
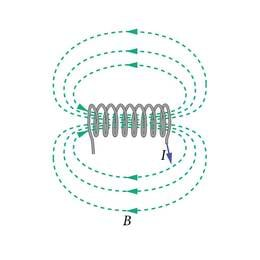
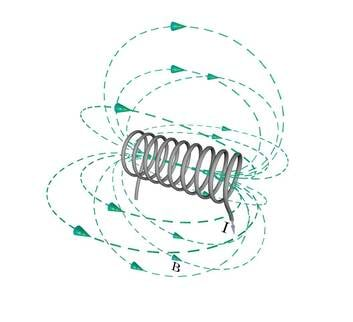
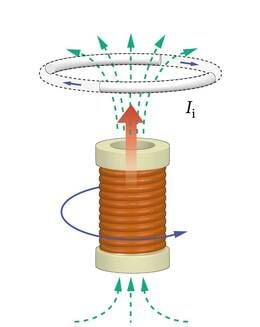
Kõrvutiasetsevatest keerdudest koosneva juhtmepooli ehk solenoidi korral liituvad solenoidi teljel paljude ringvoolude samasuunalised magnetväljad. Seetõttu on resultantväli solenoidi sees väga tugev (J.1.33). Vooluga solenoidi magnetvälja jõujoonte katseline pilt on joonisel 1.34.
Rauapuru kübemed moodustavad vooluga solenoidi sees solenoidi teljega paralleelseid ja ühtlase tihedusega ridu. Seega on magnetväli vooluga solenoidi sees homogeenne. Jõujoonte hajumine solenoidi otste juures näitab, et seal magnetväli mõnevõrra nõrgeneb. Samas puudub magnetväli väljaspool solenoidi (solenoidi kõrval) pea täiesti, sest mitte mingit rauapuru reastumist me seal ei tähelda. Olukord on analoogiline elektrivälja puudumisega väljaspool plaatkondensaatorit (p.1.6.2).
Mõistagi sõltub magnetvälja suund solenoidis voolu suunast ja on määratav parema käe rusikareegli abil, analoogiliselt ringjuhtme välja juhuga. Vooluga solenoidis tekkivat homogeenset magnetvälja tasub detailsemalt uurida põhjusel, et solenoid on üks tähtsamatest magnetismi rakendustest. Me puutume sellega veel korduvalt kokku käesoleva õpiku 2. osas.
Näeme, et püsimagneti magnetvälja jõujooned kulgevad ka väljaspool magnetit pooluselt poolusele. Läbides ka magnetit ennast, moodustavad nad ikkagi kinnisi kontuure, niisamuti nagu voolujuhtmete puhul. Seega ei ole olemas punkte, kus magnetvälja jõujooned algaksid või lõpeksid.
Välja, mille jõujooned on kinnised (alguse ja lõputa), nimetatakse solenoidaalseks väljaks ehk pöörisväljaks. Seega magnetväli on pöörisväli.
Elektrivälja jõujoon
Elektrivälja jõujoon on mõtteline joon, mille igas punktis on E-vektor suunatud piki selle joone puutujat.
Magnetvälja jõujoon
Magnetvälja jõujoon on mõtteline joon, mille igas punktis on B-vektor suunatud piki selle joone puutujat.
Homogeenne väli
Homogeenseks nimetatakse välja, mille jõujooned on omavahel paralleelsed ja konstantse tihedusega (naaberjoonte vahekaugusega).
Parema käe rusikareegel
Kui rusikasse tõmmatud parema käe väljasirutatud pöial näitab voolu suunda, siis neli kõverdatud sõrme näitavad selle voolu magnetvälja suunda (parema käe rusikareegel).
Lahendus
Ja
Elektrivälja võib iseloomustada mitte ainult jõuga, mis temas mõjub ühikulise laenguga kehale, vaid ka tööga, mida see jõud võib ära teha. Juba põhikoolis õpitud suuruseks, mis kirjeldab elektrivälja töö kaudu, on pinge. Üldiselt tähendab sõna pinge alati seda, et kohe võib midagi juhtuda. Mõelgem siinkohal väljenditele pingeline olukord või suhted on pingestunud. Seal, kus on tegu elektrilise pingega, võib meie teele juba jääda silt: Kõrgepinge, elukardetav! Mis siis ikkagi on pinge?
Mehaanika kursusest teame, et tööks nimetatakse jõu ja selle mõjumise suunal sooritatud nihke korrutist. Kui keha sooritab jõu mõjul nihke , siis töö avaldub kujul
kus on nurk jõu ja nihke suundade vahel.
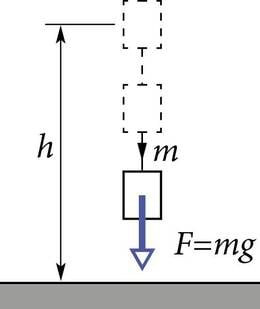
Asume uurima tööd, mida teeb kahe erinimeliselt laetud metallplaadi vahel esinev homogeenne elektriväli punktlaengu nihutamisel. Seejuures lähtume sarnasusest Maa raskusvälja ja homogeense elektrivälja vahel. Vaatleme müürilt kõrgusega alla pudenevat kivi massiga . Kivi kukub raskusväljas vaba langemise kiirendusega , sest talle mõjub raskusjõud (J.1.35).
Kivi langeb raskusjõu suunas. Järelikult töö valemis (1.18 ) ja . Maapinnale jõudmise hetkeks on kivi sooritanud nihke s ning raskusväli on seega teinud töö, mis on jõu ja sooritatud nihke (või kõrguse ) korrutis .
Kivi võib lohistada või veeretada ka mööda horisontaalset maapinda. Raskusvälja tööd see aga ei mõjuta, sest jõud ei tee tööd liikumisel jõuga ristuvas sihis (valemis 1.18 ja ).
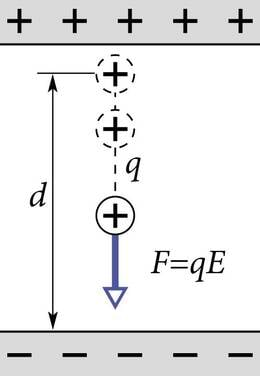
Laengut q omava keha liikumine homogeenses elektriväljas toimub samal viisil (J.1.36). Kehale mõjub elektrijõud , mis on valemi (1.11 ) kohaselt esitatav laengu ja väljatugevuse korrutisena . Kui keha on sooritanud selle jõu suunalise nihke s (või läbinud pikkuse ) siis elektriväli on teinud töö , mis on jõu ja läbitud tee pikkuse korrutis: .
Laetud keha võib samuti liikuda elektrijõuga ristuvas suunas. Elektrivälja tööd see aga ei mõjuta. Ei raskusväljas ega elektriväljas ei sõltu töö liikumistee ehk trajektoori kujust. Ta sõltub ainult jõujoone sihis läbitud pikkusest (vastavalt või ).
Välja, milles töö ei sõltu liikumistee kujust, nimetatakse potentsiaalseks väljaks, kuna tema kirjeldamisel võib kasutada potentsiaalse energia ja potentsiaali mõisteid. Potentsiaalne energia on tingitud keha vastastikmõjust teiste kehadega välja vahendusel. Kui keha asend võimaldab väljal teha keha nihutades tööd, siis on kehal potentsiaalne energia (ld potentis - suuteline, võimeline). Välja jõudude mõjul liikuva keha potentsiaalne energia kahaneb, sest töö varu kulutatakse ära.
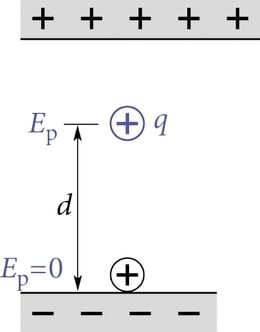
Potentsiaalse energia nulltasemeks on loomulik valida keha niisugune asend, millest keha antud ülesande tingimustes enam välja jõudude mõjul edasi liikuda ei saa. Toodud näites on selleks negatiivselt laetud plaadi asukoht (J.1.37).
Raskusjõu väljas aga on potentsiaalse energia loomulikuks nulltasemeks maapind. Sealt ei ole enam võimalik edasi kukkuda ja raskusjõud rohkem tööd teha ei saa.
Kui kogu potentsiaalne energia liikumisel ära kulutatakse, siis on tema algväärtus võrdne välja poolt tehtud tööga. Raskusväljas kehtib seega Mehaanikast hästi tuntud valem . Punktlaengu potentsiaalne energia homogeenses elektriväljas avaldub vastavalt kujul
kus on punktlaengu kaugus energia nulltasemest või pikkus, mille laetud keha saab nulltasemeni liikudes läbida. Kuna indeksita tähistab elektrifüüsikas alati väljatugevust, siis hakkame edaspidi energia tähistamiseks kasutama E-tähte koos energia liigile viitava indeksiga (siin näiteks kujul ). Väljatugevuse tähisena toimiva E-tähe juures kasutame indekseid vaid erandjuhtudel, mil väljatugevuse ja energia segiajamine on välistatud.
Nagu näeme, sisaldab energia valem nii raskus- kui elektriväljas kõigepealt vaadeldavat keha iseloomustavat suurust ( või ), seejärel välja tugevuse kirjeldajat ( või ) ning lõpuks vaadeldava punkti kaugust energia nulltasemest ( või ).
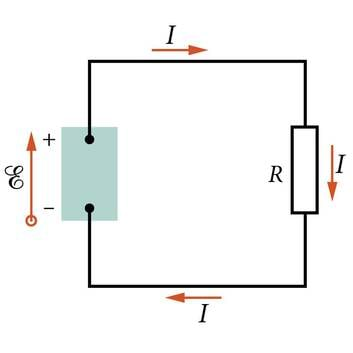
Nüüd jääb üle vaid küsida, mis on sel kõigel pistmist kodus kasutatava elektrienergiaga. Kui kummaline see ka ei tundu, on seos siiski olemas. Elektriseadmetes liiguvad laengukandjad elektrivälja jõudude mõjul. Laengukandjad liiguvad sealt, kus nende potentsiaalne energia on suur, sellisesse piirkonda, kus energia on väiksem. Seejuures teeb elektriväli meile vajalikku tööd.
Näide 1.5.
Taskulambipirni hõõgniit on 6,5 mm pikkune ja elektrivälja tugevus temas on 700 N/C. Leiame, kui palju tööd teeb elektriväli laengukandjate nihutamisel hõõgniidis ühe tunni jooksul, kui voolutugevus lambis on 0,26 A.
Lahendus
Andmed
Arvutused:
Valemist 1.2 teame, et
Seega
ja
Vastus: Laengukandjate nihutamisel hõõgniidis teeb elektriväli ühe tunni jooksul töö .
Niisama suure töö teeb raskusväli näiteks juhul, kui keha massiga kukub alla 4,3 meetri kõrguselt, seega ligikaudu teise korruse aknast. Ilmselt ei sooviks keegi meist siis parajasti all olla.
Me jõudsime äsja järeldusele, et laetud keha liikumisel elektriväljas tehtav töö võib olla üks ja seesama liikumisel mööda täiesti erinevaid teid. Järelikult pole olulised ka E-vektori pikkuse ja suuna muutused liikumise käigus. Näiteks ei sõltu elektrilambi põlemine üldse lambi hõõgniidi kujust ja E-vektori suuna muutumisest piki hõõgniiti. Oluline on vaid energia, mis vabaneb laengukandjate läbiminekul hõõgniidist. Seetõttu on elektrivälja iseloomustamiseks võetud kasutusele veel üks suurus - välja potentsiaal.
Väljatugevus E näitab teatavasti ühikulise positiivse laenguga kehale vaadeldavas punktis mõjuvat jõudu. Potentsiaal aga näitab, kui suur on selles punktis ühikulise positiivse laenguga keha potentsiaalne energia. Elektrivälja mingi punkti potentsiaali leidmiseks tuleb jagada sellesse punkti paigutatud laengu potentsiaalne energia laengu suurusega
Seejuures tähistab sõna laeng mõistagi laetud keha või laetud osakeste kogumit.
Potentsiaal on skalaarne ehk suunata suurus, nii nagu rõhk või temperatuur.
Paigutades potentsiaali definitsioonivalemisse (1.21) energia avaldise (valem 1.19), saame homogeense välja potentsiaali (J.1.38) avaldada kujul
Kehade tegelik liikumine ei sõltu kuigivõrd potentsiaali nulltaseme asukohast. Seetõttu võib potentsiaali nulltaseme valida lähtuvalt konkreetse ülesande tingimustest. Reeglina valitakse selleks punkt, millest laetud keha elektrivälja mõjul enam edasi liikuda ei saa. Elektrotehnikas loetakse tavaliselt nulliks Maa potentsiaal või siis elektriseadme maandatud metallkorpuse potentsiaal.
Ühesugust potentsiaali omavate elektrivälja punktide hulka nimetatakse ekvipotentsiaalpinnaks.
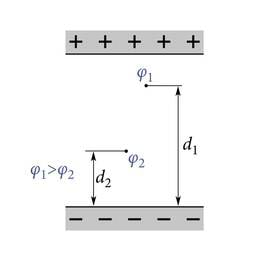
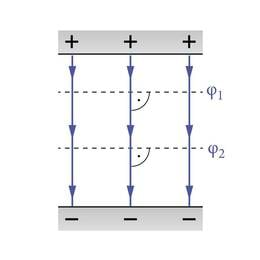
Homogeenses elektriväljas kahe erimärgiliselt laetud plaadi vahel (J.1.39) on ekvipotentsiaalpindadeks plaatidega paralleelsed tasandid. Potentsiaal muutub kõige kiiremini liikumisel piki elektrivälja jõujoont. Liikumisel jõujoonega ristuvas suunas jääb potentsiaal konstantseks.
Ekvipotentsiaalpinnad on alati jõujoontega risti. Jõujooned ja ekvipotentsiaalpinnad on kaks eri vahendit elektrivälja kirjeldamiseks. Nad on nagu kaks erinevat keelt, mis annavad edasi üht ja sama mõtet.
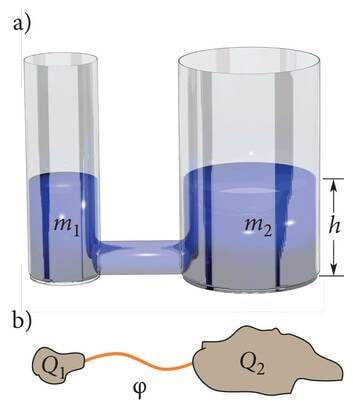
Keha liikumine potentsiaalse välja kahe punkti vahel ei sõltu punktide potentsiaalide absoluutsest suurusest. Ta sõltub vaid nende punktide potentsiaalide vahest. Nii näiteks voolab jõgi ühtemoodi aeglaselt tasasel kõrgustikualal (platool) ja merelähedasel madalal tasandikul. Voolu kiirust ei määra mitte absoluutne kõrgus (merepinnast), vaid jõe vaadeldava lõigu otspunktide kõrguste vahe. Analoogiliselt on ka laengukandjate liikumise kiirus elektriväljas määratud potentsiaalide vahega.
Elektrivälja kahe punkti potentsiaalide vahet nimetatakse elektriliseks pingeks . Potentsiaali definitsiooni (valemi 1.21) kohaselt võib pinge avaldada kujul
ja on seejuures laengut omava keha potentsiaalse energia väärtused elektrivälja kahes punktis. Nende väärtuste vahe võrdub tööga, mida teeb väli selle keha nihutamisel ühest punktist teise. Järelikult
kahe punkti vaheline pinge näitab, kui suurt tööd teeb elektriväli ühikulise positiivse laenguga keha viimisel ühest punktist teise. Laetud keha liikumisel piki jõujoont on keha nihe võrdne teekonna algus- ja lõpp-punkti vahekaugusega d ning tehtav töö avaldub kujul . Järelikult valemi 1.24 põhjal
Siit tuleneb praktiline eeskiri elektrivälja tugevuse leidmiseks. Nimelt saame elektrivälja tugevuse, jagades kahe punkti vahelise pinge nende punktide vahekaugusega , mis on mõõdetud piki välja mõjumise suunda. Seega
Valem 1.26 on täiesti täpne homogeenses elektriväljas. Mittehomogeenses väljas annab ta keskmise väljatugevuse vaadeldavas piirkonnas.
Valemiga 1.24 on määratud potentsiaali ja pinge ühik volt (1 V). Elektrivälja kahe punkti vahel on pinge üks volt, kui laengu 1 C viimisel ühest punktist teise tehakse töö 1 J. Seega
Samast seosest tuleneb töö ja energia ühik elektronvolt (1 eV). Kuna valemi 1.24 põhjal , siis üks elektronvolt on töö, mida teeb elektriväli elementaarlaengut omava osakese (elektroni) viimisel ühest punktist teise, kui pinge nende punktide vahel on üks volt.
Üks elektronvolt on järelikult sama arv kordi väiksem ühest džaulist kui mitu korda elementaarlaeng on väiksem ühest kulonist. Elektronvolt on sobivaks töö ja energia ühikuks mikromaailma protsesside kirjeldamisel, millega tutvume gümnaasiumi füüsikakursuse lõpus.
Valemi 1.26 abil on saadud elektrivälja tugevuse SI-ühik volt meetri kohta (1 V/m). See on identne valemist (1.10 ) tuleneva ühikuga 1 N/C, sest
Üks volt meetri kohta on sellise elektrivälja tugevus, milles potentsiaal muutub liikumisel piki välja suunda igal meetril ühe voldi võrra.
Pinge ja potentsiaali teema lõpetuseks meenutagem Füüsikalise looduskäsitluse aluste kursust, milles tutvusime töö kui protsessi kirjeldava suuruse ja potentsiaalse energia kui süsteemi olekut (seisundit) kirjeldava suurusega. Pole raske märgata, et Elektromagnetismis kirjeldab protsessi pinge, olukorda elektrivälja mingis punktis aga potentsiaal. Protsess viib süsteemi ühest olekust teise, mistõttu töö on kahe potentsiaalse energia vahe ning pinge kahe potentsiaali vahe. Samas võib potentsiaale vaadelda kui pingeid mingi ühise kokkuleppelise nulltaseme suhtes.
Elektrivälja tugevus juhtiva keha pinna lähedal sõltub pinna kujust. Teraviku ümbruses saavutab väljatugevus väga suure väärtuse, sest teravik käitub punktlaenguna, millele lähenemisel väljatugevus kiiresti suureneb. Elektrivälja tugevnemisega teravike läheduses võib kaasneda laengu äravool teravikelt, sest õhk teraviku ümber muutub elektrit juhtivaks. Vastavalt püütakse kõrgepingeseadmetes vältida teravaid nurki ja väljaulatuvaid osi. Ka välgueelne elektriväli õhus on kõige tugevam maast lähtuva teraviku läheduses. Seetõttu on hoonetele parimaks kaitseks piksevarras. Välgulöök tabab suure tõenäosusega eelkõige piksevarrast, aga mitte hoonet.
Kui välk lööb maasse, siis on maapinna potentsiaal välgust tabatud kohas hetkeks oluliselt erinev Maa üldisest potentsiaalist. Selle tagajärjel muutub potentsiaal piki maapinda lähenemisel välgust tabatud kohale. Mida rohkem on inimese üks jalg välgutabamuse asukohale lähemal kui teine, seda suurem potentsiaalide erinevus (pinge) tekib tema kahe jala vahel. Niisugust pinget nimetatakse sammupingeks. Sammupinge võib esineda ka elektrijuhtmestiku rikke tagajärjel. Igatahes on elektriohu korral soovitav liikuda võimalikult lühikeste sammudega, et vältida suure sammupinge tekkimist.
Äikese ajal pole soovitav ujuda või sõita paadiga. Välisantenni kasutamise korral ei maksa äikese ajal vaadata telerit. Tasub hoiduda ahju kütmisest, kuna suitsusammas sisaldab harilikust õhust oluliselt rohkem laetud osakesi. Seetõttu võib välk tema kaudu majja sisse lüüa.
Elektrivälja potentsiaal
Elektrivälja potentsiaal näitab, kui suur on vaadeldavas punktis ühikulise positiivse laenguga keha potentsiaalne energia.
Ekvipotentsiaalpinnad
Ühesugust potentsiaali omavate elektrivälja punktide hulka nimetatakse ekvipotentsiaalpinnaks.
Elektriline pinge
Elektrivälja kahe punkti potentsiaalide vahet nimetatakse elektriliseks pingeks. Kahe punkti vaheline pinge näitab, kui suure töö teeb elektriväli positiivset ühikulist laengut omava keha viimisel ühest punktist teise.
Kulon, džaul ja volt
Kui laengu 1 C viimisel ühest punktist teise teeb elektriväli töö 1 J, siis on pinge nende punktide vahel üks volt (1 V).
Ei ole üldse kindel, et Benjamin Franklin oma lohekatset ka tegelikult tegi. Jah, ta kirjeldas sellist katset oma 1750 a. artiklis, aga ta andis endale ka aru ohtudest, mis sellise katse tegijat ähvardavad. Nii hästi ei läinud Peterburis töötanud Saksa päritolu teadlasel Georg Wilhelm Richmann’il, kes välgutabamuse saanud lohe tekitatud plahvatuses surma sai. Igal juhul sai 18. sajandi lõpul kinnitust hüpotees, et välk on elektriline nähtus ja majad said endale Franklini leiutatud väga kasuliku seadeldise - piksevarda.
Jaapanis, Tokyo ja Nagoya vahel on kõigil huvilistel võimalik sõita rongiga, mis hõljub oma "rööbaste" kohal ja sõidab sealjuures kiirusega kuni 600 km/h, ehk vahemaa Tartu ja Tallinna vahel läbiks selline rong vähem kui poole tunniga. Öeldakse, et sellised rongid kasutavad "magnetilist levitatsiooni". Tõepoolest, teame hästi, et kaks magnetit võivad tõukuda, aga see ei saa olla kogu tõde - üks magnet ei jää teise kohale hõljuma, ükskõik kui hoolikalt me neid üksteise suhtes ka ei asetaks.
Selgub, et elektri- ja magnetnähtuste ampluaa muutub tohutult rikkalikumaks, kui me paneme laengud ja magnetid liikuma. Sest tekivad elektromagetväljad.
Käesolevas peatükis asume käsitlema elektri- ja magnetvälja muutumist ajas. Vaatleme ka kahe välja sügavamaid omavahelisi seoseid ning vastastikuseid muundumisi.
Seejuures tuleb enamasti eeldada laetud osakeste mitteühtlast (kiirenevat või aeglustuvat) liikumist. Samuti pole elektri- ja magnetvälja enam võimalik vaadelda teineteisest lahus. Tegemist on elektromagnetilist vastastikmõju vahendava ühtse elektromagnetväljaga. Selle välja uurimise muudab keeruliseks protsesside tagasisidestatus. Tagasiside on nähtus, mille korral ühe füüsikalise suuruse muutumine põhjustab teiste suuruste selliseid muutusi, mis omakorda mõjutavad esimest suurust. Näiteks põhjustab pendli hälbe suurenemine tasakaaluasendi poole suunatud jõu kasvamist. See jõud aga pidurdab hälbe kasvu ja pendli liikumine aeglustub. Antud juhul pidurdab teise suuruse (jõu) muutus esimese suuruse (hälbe) muutumist. Selle kohta öeldakse, et hälbe muutus on negatiivselt tagasisidestatud. Elektromagnetvälja korral on igasugune elektrivälja muutus tagasisidestatud temaga kaasneva magnetvälja muutuse kaudu. Kui laetud keha vaatleja suhtes liigub, siis muutub keha elektriväli vaatleja asukohas ning vaatleja registreerib ka magnetvälja (J.2.1). Peagi veendume, et see kõik kehtib ka ümberpöördult. Kui magnetvälja tekitaja (püsimagnet) vaatleja suhtes liigub, siis muutub magnetväli vaatleja asukohas ning vaatleja täheldab ka elektrivälja olemasolu (J.2.2). Magnetvälja muutumine tekitab elektrivälja. Seda nimetatakse elektromagnetilise induktsiooni nähtuseks. Märkigem veel, et võõrsõna indutseerima eestikeelseks vasteks ongi tekitama või esile kutsuma.
Juba põhikooli Elektriõpetuses saime teada, et elektromagnetilisel induktsioonil põhineb generaatori töö. Teatavasti muundab generaator mehaanilist energiat elektrienergiaks, olles nii keskses rollis elektrienergia tootmisel. Elektromagnetnähtuste tundmaõppimine võimaldab meil mõista seda inimkonnale üliolulist protsessi.
Käesolevas peatükis vaatleme siis lähemalt, kuidas muutuv magnetväli saab tekitada elektrivälja. Loomulikult teeme ka kindlaks, millest sõltub vastav väljatugevus või pinge. Lõpuks uurime, mismoodi võib elektromagnetväljas salvestuda energia.
Selleks, et kirjeldada laengukandjate liikumist elektriväljas, mis tekib magnetvälja muutumisel, peame kõigepealt tutvuma magnetväljas liikuvale laetud osakesele mõjuva jõuga. Seda jõudu nimetatakse hollandi füüsiku Hendrik Antoon Lorentz'i (1853 – 1928) auks Lorentzi jõuks.
Juhtmelõigule, mille pikkus on ja milles kulgeb vool tugevusega , mõjub teatavasti magnetväljas induktsiooniga magnetjõud . Selle jõu suurus on leitav Ampère'i seadusest (valem 1.12)
kus on nurk voolu suuna ja magnetvälja suuna vahel. Voolu olemasolu tähendab laengukandjate suunatud liikumist keskmise kiirusega . Mõistagi osalevad laengukandjad ka kaootilises (kindla suunata) liikumises, aga see meid praegu ei huvita. Jõud Ampère'i seaduses summeerub üksikutele liikuvatele laengukandjatele mõjuvatest Lorentzi jõududest. Seega tuleb Lorentzi jõu leidmiseks jagada juhtmele kui tervikule mõjuv magnetjõud liikuvate laengukandjate arvuga :
Vaatleme laengukandjaid, mis liiguvad keskmise kiirusega läbi silindrikujulise juhtmelõigu (J.2.3).
Kui juhtmelõigu pikkus on parajasti võrdne korrutisega (Mehaanika kursuse valem ), siis jõuavad kõik silindris sisalduvad laengukandjad aja jooksul juhtmelõigust läbi tagumise otsapinna väljuda. Laengukandjatel, mis on tagumisele otsale lähemal kui , kulub selleks mõistagi seda vähem aega, mida väiksem pikkus neil läbida tuleb, aga aja jooksul väljuvad kõik laengukandjat. Nende kogulaeng on , kus on ühe laengukandja laeng.
Voolutugevuse definitsiooni (valem 1.1) põhjal saame, et:
Järelikult on Lorentzi jõu vektori pikkus esitatav kujul
kuna juhtmelõigu pikkuse ja laengukandjal selle läbimiseks kulunud aja suhe võrdub laengukandja suunatud liikumise kiirusega . Niisiis mõjub laengut omavale ja kiirusega liikuvale osakesele magnetväljas induktsiooniga Lorentzi jõud
kus on nurk osakese liikumissuuna (kiirusvektori) ja magnetvälja suuna (B-vektori) vahel (J.2.3). Kuna positiivse laenguga osakesed liiguvad voolu kokkuleppelises suunas, siis võib neile mõjuva Lorentzi jõu suuna määrata vasaku käe reegli abil, mis antud juhul kõlab järgmiselt. Kui vasaku käe väljasirutatud sõrmed näitavad positiivselt laetud osakese liikumise suunda ja magnetvälja jõujooned tulevad peopessa, siis väljasirutatud pöial näitab osakesele mõjuva Lorentzi jõu suunda (J.2.4).
Elektroni kui negatiivselt laetud osakese korral on Lorentzi jõu suund eelnevale vastupidine, sest valemisse 2.1 ilmub miinusmärk. Elektronile mõjuva Lorentzi jõu suunda näitab analoogiliselt paikneva parema käe pöial.
Tasub rõhutada, et Lorentzi jõud mõjub laetud osakestele alati risti nii liikumissuuna kui ka magnetvälja suunaga. Seetõttu ei saa Lorentzi jõud liikumisel tööd teha. Ta võib vaid muuta liikumise suunda. Kõige tugevam on Lorentzi jõud liikumissuunaga ristuvas magnetväljas. Sel juhul ja järelikult
Kui laengukandja kiirusvektor on risti magnetvälja suunaga (B-vektoriga), siis paneb Lorentzi jõud vaakumis asetseva laengukandja liikuma piki ringjoont ümber magnetvälja suuna, toimides kesktõmbekiirendust andva jõuna. Kui laengukandja liigub piki magnetvälja suunda (v- ja B-vektorid on samasihilised), siis Lorentzi jõudu ei teki, sest on ja seega ka .
Lorentzi jõu mõju kohta on ka palju demoeksperimente, kus elektronkiir magnetvälja mõjul oma suunda muudab.
Selgitavad joonised selle katse kohta:
| Madala rõhu all oleva gaasiga täidetud kambris tiirlevad elektronid (nende orbiit on nähtav helenduva rõngana). Kambrit täidab ühtlane magnetväli, mis on suunatud otse lehekülje tasandist välja. Paneme tähele, et elektronide ringliikumise saavutamiseks peab magnetjõud Fm olema suunatud radiaalselt ringi keskmesse. Ja tõepoolest, valem 2.1 ja parema käe reegel negatiivselt laetud osakeste jaoks ennustavad selle eksperimendi tulemust õigesti. | 3D mudel seletab Lorentzi jõudude mõju homogeenses magnetväljas liikuvale elektrilaengule. |
Kui v- ja B-vektorite vahel on suvaline nurk, siis võime laengukandja kiiruse lahutada kaheks komponendiks: B-vektoriga ristuvaks ja B-vektoriga paralleelseks . Ristuva komponendi olemasolu põhjustab laengukandja täiendava ringjoonelise liikumise ümber magnetvälja suuna. Sellega kaasneb laengukandja liikumine kiirusega piki magnetvälja suunda. Tulemusena liigub laengukandja mööda kruvijoont (ruumilist spiraali). Nii liiguvad näiteks kosmilise kiirguse laetud osakesed Maa ionosfääris piki spiraale, mille telgedeks on Maa magnetvälja jõujooned. Pannes kosmilise kiirguse osakesed ümber Maa spiraalima, kaitseb Maa magnetväli otsese kosmilise kiirguse eest kõike elusat Maa peal.
| Virmaliste ovaal, mis ümbritseb maakera geomagnetilist poolust (see asetseb praegu Gröönimaa kirdeosas). Magnetvälja jõujooned koonduvad pooluse suunas. Maa poole liikuvad elektronid püütakse kinni ja need liiguvad spiraalselt ümber magnetvälja jõujoonte, sisenedes Maa atmosfääri suurematel laiuskraadidel ja tekitades ovaalis virmalisi. | Virmalisi on aeg-ajalt näha ka Eestis. Sellistena paistavad nad rahvusvahelise kosmosejaama pardalt. |
Elektromagnetväli
Elektromagnetväljaks nimetatakse elektromagnetilist vastastikmõju vahendavat välja, mille piirjuhtudeks on elektriväli ja magnetväli.
Elektromagnetilise induktsiooni nähtus
Elektromagnetilise induktsiooni nähtuseks nimetatakse elektrivälja tekkimist magnetvälja muutumisel.
Esimeses peatükis vaatlesime vooluga juhtmele mõjuvat magnetjõudu. Asume nüüd uurima mootori mähisekeeru lõiku ab, mis generaatorina toimivas mootoris liigub ülespoole mitte enam magnetjõu vaid masina võlli päripäeva pöörava välisjõu toimel (J.2.7). Laengukandjad juhtmelõigus ab liiguvad koos juhtmega. Magnetväljas liikuvatele laetud osakestele mõjub aga teatavasti Lorentzi jõud, mis positiivsetele laengukandjatele rakendub vasaku käe reegli kohaselt "meist eemale" ehk suunas a→b. Analoogiliselt mõjub juhtmelõigus cd positiivse laengu kandjatele jõud suunas c→d ehk "meie poole". Järelikult hakkavad positiivsed laengukandjad vaadeldavas juhtmekeerus Lorentzi jõu mõjul liikuma suunas a→b→c→d. Juhtmekeeru otste a ja d ühendamisel moodustub vooluring, milles keeru pööramise tulemusena kulgeb elektrivool. Juhtme liikumine magnetväljas tekitab juhtmes induktsioonivoolu, mille suund on vastupidine mootori korral toiteallika poolt tekitatud voolule. Nende kahe voolu vastassuunalisuses juhtmelõigu sama liikumissuuna korral avaldub Lenzi reegel, millega me hiljem (p.2.5.1) tegeleme pikemalt. Samas ei tohi unustada, et mootori korral on uuritav mähisekeerd tarviti, generaatoris aga vooluallika rollis.
Olgu öeldud, et nii sellel kui ka kõigil järgnevatel joonistel on jämeda noolega tähistatud juhtmelõigu liikumise suund. Samuti uurime nii siin kui ka edaspidi positiivsete laengukandjate liikumist, ehkki tegelikult on metalljuhtmes laengukandjateks negatiivsed juhtivuselektronid. Niisugune lihtsustus on põhjendatud, sest voolu suund ühtib voolu tekitava elektrivälja suunaga ega sõltu laengukandjate märgist (p.1.2.6).
Voolu uuritavas mähisekeerus võib vaadelda tingituna elektriväljast, mille jõujooned on kontuuri abcd suunalised kinnised jooned. Meenutagem siinkohal FLA (Füüsikalise looduskäsitluse aluste) kursust, mida alustasime tõdemusest, et iga vaatleja loob füüsikalise maailmapildi omaenda aistingute või mõõtmistulemuste põhjal. Kui vaatleja täheldab elektrivoolu olemasolu ning teab, et vool on tingitud samas suunas toimivast elektriväljast, siis on vaatleja registreerinud ka elektrivälja. Selle elektrivälja tekkepõhjuseid võib vaatleja edaspidi uurida, kuid tal pole põhjust kahelda välja olemasolus. Magnetvälja muutumisel tekkiva elektrivälja suhtes pole enam rakendatav potentsiaali mõiste. Meil ei ole ju mingit alust eelistada suletud kontuuri mingit kindlat punkti teistele ja väita, et just selle punkti potentsiaal on kõrgem kui mõnel teisel punktil. Tekkiv elektriväli ei ole potentsiaalne, tema jõujooned on alguse ja lõputa kinnised jooned ehk pöörised. Seetõttu nimetatakse niisugust elektrivälja pööriselektriväljaks.
On märkimisväärne, et kirjeldatud juhul liigub juhtmelõik homogeenses magnetväljas. B-vektor on liikumistee eri punktides ühesugune nii suuruselt kui suunalt. Miks me siis ikkagi võime rääkida magnetvälja muutumisest juhtmelõigu asukohas? Me teeme seda põhjusel, et juhe liigub magnetvälja tekitaja suhtes risti välja suunaga ning lõikab magnetvälja jõujooni. Näiteks liikumisel magnetvälja suunas juhe jõujooni ei lõika (J.2.8). Sellisel liikumisel laengukandjatele magnetjõudu ei mõju, kuna Lorentzi jõu valemis
on nurk võrdne nulliga. Järelikult ei teki sel juhul ka induktsioonivoolu.
Juba põhikooli Elektriõpetuses liiguti magnetjõu tekkimise juurest elektromagnetilise induktsioonini (p.2.2.1). Seega tasub meil neid kahte nähtust omavahel võrrelda ka siin. Vaatleme veelkord paremale suunatud magnetväljas asetsevat horisontaalset juhtmelõiku (elektrimootori mähise osa ab).
Kui me tekitame selles juhtmes meie poole suunatud voolu I, siis hakkab juhtmele Ampere’i seaduse ja vasaku käe reegli kohaselt mõjuma ülespoole suunatud magnetjõud (J.2.9). Võimaluse korral hakkab juhe selles suunas liikuma. Kirjeldame nähtust kokkuvõtlikult kujul:
elektrivool + magnetväli → liikumine.
| J.2.9 Magnetväljas asuvale vooluga juhtmele mõjuv jõud. Kui me tekitame selles juhtmes meie poole suunatud voolu I, siis hakkab juhtmele Ampère'i seaduse ja vasaku käe reegli kohaselt mõjuma ülespoole suunatud magnetjõud. Võimaluse korral hakkab juhe selles suunas liikuma. | J.2.10 Juhtmes, mis liigub magnetväljas, tekib vool. Laengukandjad juhtmes liiguvad koos juhtmega üles ja neile hakkab mõjuma meist eemale suunatud Lorentzi jõud FL. Juhtmes tekib induktsioonivool Iind. |
Joonisel 2.10 on aga näha, mis juhtub siis, kui me niisugust magnetväljas asetsevat juhet ise ülespoole liigutame. Laengukandjad juhtmes liiguvad koos juhtmega üles ja neile hakkab mõjuma meist eemale suunatud Lorentzi jõud . Juhtmes tekib induktsioonivool . Nähtust võib kokkuvõtlikult kirjeldada kujul:
magnetväli + liikumine → elektrivool.
Niisiis on elektromagnetilise induktsiooni näol tegemist omalaadse pöördprotsessiga magnetjõu tekkimisele.
Pööriselektrivälja jõujooned on kinnised, alguse ja lõputa jooned, nii nagu magnetvälja jõujoonedki. Jõu mõjul liikuvat juhtmelõiku ümbritseb ja läbib pööriselektriväli samamoodi nagu magnetväli ümbritseb ja läbib püsimagnetit (J.2.11).
Vaatleme nüüd isoleeritud juhtmelõiku, mis liigub kiirusega magnetväljaga ristuvas suunas ning on ka ise risti selle suunaga (J.2.12). Koos juhtmega üles liikuvatele positiivsetele laengukandjatele (laenguga ) mõjub Lorentzi jõud . Laengukandjad liiguvad selle magnetjõu mõjul piki juhet tahapoole, aga juhtmest välja nad ei pääse. Juhtme otsad laaduvad erimärgiliselt ja juhtmes tekib ettepoole suunatud elektriväli. Laengukandjate liikumine kestab seni, kuni neile mõjuv elektrijõud (valem 1.11) magnetjõu tasakaalustab. Vastav elektrivälja tugevus on väljendatav pinge kaudu (valem 1.26)
kus on juhtmelõigu pikkus ( algkujus tähis ). Tasakaalu tingimuse võib siis esitada kujul
millest tulenevalt võime juhtmelõigu otstele indutseeritava pinge avaldada kujul
Juhul kui juhtme liikumissuund moodustab magnetväljaga mingi nurga , mis ei ole täisnurk, siis põhjustab Lorentzi jõudu vaid liikumissuunaga ristuv B-vektori komponent (J.2.13). Liikumisel magnetvälja sihis ju teatavasti magnetjõudu ei teki (p.2.1.3). Indutseeritud pinge avaldis võtab kuju
Näide 2.1.
Tartu-Tallinna kiirrong sõidab kiirusega 108 km/h maa magnetvälja horisontaalkomponendi suunas. Kui suur pinge tekib elektromagnetilise induktsiooni tõttu vaguniratta telje otstele? Rööbaste vahekaugus on 1524 mm ja Maa magnetinduktsiooni vertikaalkomponent Eestis 48 μT.
Lahendus
Andmed
Arvutused
Rattatelg on vaadeldav kui juhtmelõik, mis on risti nii oma liikumissuuna kui ka magnetinduktsiooni vertikaalkomponendiga , seejuures .
Kasutades valemit
saame kirjutada:
Vastus: Telje otste vahel tekib pinge . Praktikas jäetakse see pinge tema väiksuse tõttu arvestamata.
Eelmises punktis jõudsime magnetvälja suhtes liikuvas isoleeritud juhtmelõigus indutseeritud pinge avaldiseni. Seejuures tuginesime oma teadmistele Lorentzi jõu kohta. Elektromagnetilise induktsiooni avastajal Michael Faraday'l neid teadmisi ei olnud. Faraday uuris kinnisi vooluringe, määrates voolutugevust magnetnõela kõrvalekaldumise järgi tasakaaluasendist (Oerstedi katse, p.1.4.2). Kuid Faraday mõistis, et laengukandjate liikumapanemiseks tuleb teha tööd. Kirjeldamaks laengukandjate liikumapanemisel kinnises kontuuris tehtavat tööd hakkas Faraday kasutama elektromotoorjõu mõistet (electromotive force – EMF, vastav eestikeelne lühend EMJ).
Elektromotoorjõud (tähis ehk suur ümmargune E) iseloomustab üldjuhul vooluallikas toimivaid mitteelektrilisi jõude ehk kõrvaljõude. Elektrivoolu püsimiseks keemilist vooluallikat (patareid või akut) sisaldavas vooluringis tuleb vooluallika positiivselt pooluselt ehk plussklemmilt läbi vooluringi miinusklemmile jõudnud positiivsed laengukandjad viia läbi vooluallika uuesti plussklemmile. Järelikult tuleb neid nihutada vastupidiselt elektrijõu suunale. Seda suudavad teha ainult kõrvaljõud. Elektromotoorjõud on võrdne kõrvaljõudude tööga Ak ühikulise suurusega laengu ühekordsel läbiviimisel kogu vooluringist:
| J.2.14 Lihtne elektriline vooluring, milles EMJ tekitav seade teeb tööd laengukandjate nihutamisel ja säilitab takistis takistusega R ajas muutumatu voolu I. | Maailma suurim energiat salvestav akupatarei (lammutatud aastal 1996) ühendas rohkem kui 8000 suurt pliiakut 8 ahelaks, igaüks võimega anda 10 MW elektrilist võimsust 4 tunni jooksul. Seda laeti öösel ja pandi elektrisüsteemis tööle päeval elektrienergia tippnõudluse tundidel. |
Keemilise vooluallika korral teeb kõrvaljõud selle töö ära vooluallika sees, tekitades vooluallika pooluste vahel elektrivälja, mistõttu laengukandjad saavad väljaspool vooluallikat ehk vooluringi välisosas liikuda juba elektrijõu mõjul. See energia, mille arvel laengukandjad suunatud liikumist takistavate jõudude kiuste kogu vooluringi läbivad, tuleb lõppkokkuvõttes kõrvaljõult. Keemilise vooluallika korral on laengukandjate liikumine vahetult kõrvaljõu toimel vooluallika sees ja elektrijõust põhjustatud laengukandjate liikumine vooluringi välisosas ruumiliselt lahutatud. Seepärast võime EMJ käsitleda kui suurimat pinget, mida keemiline vooluallikas on suuteline oma klemmidele tekitama. Elektromagnetilise induktsiooni korral võib aga üksainus kinnine juhtmerõngas olla üheaegselt nii vooluallika kui vooluringi välisosa rollis. Kõrvaljõu ja elektrijõu toimete ruumilist lahutatust ei ole ning potentsiaali ja pinge mõistetel puudub sisu, kui tõlgendada pinget vaid elektrijõudude tööna ühikulise laengu viimisel ühest punktist teise (p.1.7.4). See ongi peapõhjuseks, miks jätkuvalt kasutatakse kõlaliselt mõnevõrra eksitavat mõistet elektromotoorjõud. EMJ pole ju jõud ja tema ühikuks pole njuuton. EMJ on töö ja laengu suhe ehk pinge ja tema ühikuks on volt. Kuid nii öeldes peame mõistma pinge all kõigi liikumapanevate jõudude (ka kõrvaljõudude) tööd ühikulise laengu nihutamisel. Olles selles kokku leppinud, võime EMJ käsitleda kui kõikide pingete summat kinnises vooluringis.
Seni vaadeldud näidetes on kõrvaljõuks just seesama jõud, mis liigutab juhet või pöörab generaatori võlli magnetväljas.
Mingi juhtmelõigu liigutamisel magnetväljas tuleb teha tööd mitte ainult mehaanilise hõõrdejõu ületamiseks, vaid ka laengukandjate liikumapanemiseks juhtmega ühendatud vooluringis, juhul kui see vooluring on olemas. Elektromagnetilist induktsiooni võib vaadelda kui omalaadset ,,lisahõõrdumist" magnetväljas. Kui induktsioonivool viib positiivse ühikulise laengu üks kord läbi tekkiva vooluringi, siis kõrvaljõu poolt selleks tehtavat tööd nimetatakse induktsiooni elektromotoorjõuks. Ülaltoodu põhjal võib induktsiooni elektromotoorjõudu tõlgendada ka kui pinget, mis tekib katkestuskohas, kui me kasutame elektromagnetilisel induktsioonil põhinevat vooluallikat ja katkestame kuskil vooluringi. Lihtsaimaks selliseks vooluallikaks ongi liikumisel magnetvälja jõujooni lõikav juhtmetükk (p.2.2.2).
Induktsioonivoolu tekkimine
Jõud, mis nihutab juhet magnetväljas, paneb elektromagnetilise induktsiooni teel laengukandjad juhtmes liikuma. Kui liikuv juhe on osa vooluahelast, siis esineb selles ahelas induktsioonivool.
Pööriselektriväli
Pööriselektriväljaks nimetatakse elektrivälja, mille jõujooned on kinnised jooned ehk pöörisjooned. Selline elektriväli tekib magnetvälja muutumisel.
Suure avastuse sünnihetk on teaduse ajaloos harva teada kuupäevalise täpsusega. Elektromagnetilise induktsiooni avastamine kuulub aga nende harvade erandite hulka. See on nii tänu avastuse autori Michael Faraday täpsetele ülestähendustele. 29. augustil 1831 kirjutas Faraday laboripäevikusse, et raudsüdamikule mähitud juhtmepooli ühendamine vooluallikaga kutsub esile lühiajalise voolu ka teises, samale südamikule keritud poolis. Sama aasta 17. oktoobril tehtud sissekanne kõneleb aga voolu registreerimisest poolis, millele mõjuvat magnetvälja püsimagneti nihutamise teel muudeti.
Juba aastal 1822, kaks aastat pärast elektrivoolu magnetilise toime avastamist Oerstedi ja Ampere'i poolt, tuli Faraday mõttele, et see nähtus peaks esinema ka ,,tagurpidi". Kui elektrivool tekitab magnetvälja, kas ei võiks siis magnetvälja abil tekitada elektrivoolu? Aastal 1825 asus Faraday seda oletust katseliselt kontrollima, kuid ei suutnud induktsioonivoolu avastada. Faraday ei mõistnud siis veel, et elektrivälja tekitab mitte magnetväli ise, vaid magnetvälja muutumine. Pealegi ei olnud Faraday käsutuses piisavalt tundlikku mõõteriista. Voolu mõõtis Faraday magnetnõela pöördumise järgi vooluga juhtme läheduses (Oerstedi katse).
| Algelised induktiivelemendid, millega katsetades Michael Faraday induktsiooniseaduse avastas. Tol ajal ei olnud veel saadaval isoleeritud juhtmeid. Räägitakse, et Faraday isoleeris juhtmeid riideribadega, mis olid lõigatud tema naise ühest alusseelikust. | Huvitav on ehk teada, teadusteater oli populaarne juba 19. sajandil. Faraday eksperimente tegemas oma 1856. aasta jõuluetendusel. |
1831. aasta suvel asus Faraday taas korraldama samalaadseid uuringuid. Nüüd aga tugevdas ta pooli magnetvälja raudsüdamiku abil. Magnetvälja järsk muutmine tekitas samal südamikul paiknevas teises poolis vooluimpulsi. Elektromagnetiline induktsioon oli avastatud.
Faraday tegi elektromagnetilise induktsiooni uurimisel väga palju katseid. Kui kasutada on tester või mõni muu voolutundlik mõõteriist, siis võib neid katseid vastava huvi olemasolu korral teostada ka kodustes tingimustes. Faraday katsed võiks jagada kolme gruppi, mida järgnevalt ka eraldi vaatleme.
Põhiliseks katsevahendiks elektromagnetilise induktsiooni uurimisel on torukujulisele isoleerivale südamikule keritud juhtmepool. Kõigis allpool kirjeldatud katsetes on vaja koguni kahte niisugust pooli. Pooli võib valmistada ka ise sobiliku jämedusega (0,3-0,5 mm) vasktraadist. Sellist traati võib osta enam-vähem suvalisest elektridetailide poest.Traat tuleb tihedalt kerida silindrilisele papist või plastikust torukesele. Mähis võiks olla 2-3 cm pikkune ja sisaldada ülestikku vähemalt 5 kihti kõrvutiasetsevaid juhtmekeerde. Et mähis traadi elastsuse tõttu laiali ei laguneks, on soovitatav iga kiht pärast kerimise lõpetamist kleepribaga fikseerida.
Sellise katseseadmega on lihtne veenduda, et muutuv magnetväli kutsub poolis esile induktsioonivoolu. Tekkinud voolu võib registreerida tundliku ampermeetrina töötava testri abil. Magnetvälja on kõige lihtsam muuta, torgates pikergust püsimagnetit pooli sisse.
Kirjeldatud katse on põhimõtteliselt teostatav ka üheainsa juhtmekeeruga. Niisugusel juhul on tekkiv induktsioonivool aga niivõrd nõrk, et seda on raske mõõta. Pooli korral liituvad üksikutes keerdudes tekkinud elektromotoorjõud, sest keerud toimivad jadamisi ühendatud vooluallikatena. Seetõttu saame ka mõõtmiseks piisavalt tugeva induktsioonivoolu. Voolu indutseerimist üksikus juhtmekeerus selgitab joonis 2.16. Näiteks liigub juhtmelõik dc täpselt samamoodi paremale suunatud magnetväljas allapoole nagu lõik dc joonisel 2.6. Lõigus dc indutseeritakse selle tagajärjel meie poole (c→d) suunatud vool. Seevastu lõigus gh kulgeb induktsioonivool meist eemale (g→h) ja juhtmekeerus tervikuna (ülalt vaadates) päripäeva.
Parema käe rusikareegli (J.2.17) abil võib veenduda selles, et induktsioonivoolu magnetväli on joonisel suunatud ülalt alla, niisiis vastupidiselt juhtmekeerus tugevnevale püsimagneti väljale. Induktsioonivool takistab sellesama magnetvälja kasvu, mis voolu esile kutsus. Tasub ka rõhutada, et induktsioonivool on olemas vaid seni, kuni juhtmekeerd püsimagneti jõujoonte suhtes liigub. Kui lõpeb liikumine, siis saab laengukandjatele mõjuv Lorentzi jõud nulliks, sest .
Magnetvälja põhjustajana võib püsimagneti asemel kasutada ka vooluga pooli.
Kui me asendame joonisel 2.16 kujutatud katses püsimagneti pooliga (J.2.18), siis tekib ülemises juhtmekeerus induktsioonivool täpselt samamoodi nagu püsimagneti korral. Nii on see muidugi eeldusel, et juhtmekeerdu lähendatakse poolile ja pooli magnetväli on suunatud alt üles. Pooli magnetväljal on selline suund juhul, kui vool pooli keerdudes kulgeb ülalt vaadates vastupäeva (meie silme ees vasakult paremale). Induktsioonivool ise on kirjeldatavas katses teatavasti suunatud päripäeva (külgvaates paremalt vasakule). Seega on induktsioonivoolu suund vastupidine voolu suunale indutseerivat magnetvälja tekitavas poolis. Püüdkem iseseisvalt veenduda selles, et juhtmekeeru kaugenemisel poolist on ka induktsioonivool suunatud vastupäeva. Mõlemad vaadeldavad voolud on sel juhul samasuunalised.
Katsetamisel südamikuta poolidega võib induktsioonivool osutuda liiga nõrgaks. Sel juhul võib voolu tugevdada, paigutades eelnevalt poolide sisse raudsüdamikud (näiteks suured raudpoldid). Rauas on magnetinduktsioon palju suurem kui õhus. Seetõttu on suuremad ka magnetinduktsiooni muutused, millest omakorda sõltub induktsioonivoolu tugevus.
Analoogilised nähtused leiavad aset ka kahe paralleelse sirgjuhtme korral, millest ühes voolab alalisvool (J.2.19). Kui me nihutame üht juhet teisele lähemale, siis lõikavad vooluga juhtme 1 magnetvälja jõujooned vooluta juhet 2. Vasaku käe reegli kohaselt mõjub positiivsetele laengukandjatele juhtmes 2 meie poole suunatud Lorentzi jõud. Juhtmes 2 tekib seeläbi induktsioonivool, mille suund on vastupidine juhtmes 1 kulgeva voolu suhtes. See arutlus jääb kahjuks vaid teoreetiliseks, sest üksiku voolujuhtme magnetväli on väga nõrk ja tekkivat induktsioonivoolu on väga raske mõõta.
Kõigil seni vaadeldud juhtudel põhjustab elektromagnetilist induktsiooni puhtmehaaniline liikumine. Uuritav juhe liigub magnetvälja tekitaja suhtes. See aga ei pea alati nii olema. Magnetvälja võib muuta ka seda välja tekitava voolu muutmise teel juhtmes, nii et juhtmed jäävad paigale. Teatavasti toimis just nii ka Faraday oma esimeses katses.
Vaatleme näitena jällegi kahte paralleelset sirgjuhet, millest üks on läbi lüliti ühendatud vooluallikaga (J.2.20, a). Lüliti sulgemisel suureneb voolutugevus juhtmes nullist kuni mingi lõppväärtuseni . Vastavalt kasvab ka selle voolu magnetväli. Magnetvälja tugevnemine on aga samaväärne lähenemisega välja tekitavale juhtmele. Me teame ju (, p.1.5.3), et vooluga sirgjuhtme magnetinduktsioon on pöördvõrdeline kaugusega sellest juhtmest.
Niisiis mõjub juhtmest 1 tingitud magnetvälja levik juhtme 2 suunas (J.2.20, b) laengukandjatele samamoodi nagu juhtme 2 liikumine juhtme 1 poole. Eelmisest alapunktist teame, et seda laadi liikumine indutseerib juhtmes 2 meie poole suunatud voolu (J.2.19). Voolu sisselülitamine juhtmes tekitab vastupidise suunaga voolu naaberjuhtmes. Lõpetuseks märkigem, et kõik senised järeldused oleme me teinud, lähtudes teadmistest Lorentzi jõu kohta. Faraday jõudis samade järeldusteni katsetulemusi üldistades.
Oleme nüüd päris palju tegelenud pööriselektrivälja tekkimisega magnetvälja muutumisel. Aga mis tähendus on üleüldse sõnadel magnetväli muutub? Millise füüsikalise suuruse muutumisest on jutt? Elektromagnetilise induktsiooni nähtus esineb teatavasti ka homogeenses magnetväljas (p.2.2.1). Seega ei saa otsitavaks muutuvaks suuruseks olla magnetinduktsioon . Vajalik suurus tuleb meil alles määratleda. Järgnevas katseseerias uurime, millest sõltub induktsiooni elektromotoorjõud.
| Ühendame juhtmepooli külge voolutundliku mõõteriista. Kinnitame pooli sisse mahtuva raudpoldi otsa tugeva püsimagneti, muutes niiviisi ka poldi magnetiks. Pistame nüüd poldi pooli sisse, tehes seda ligikaudu ühe sekundi jooksul ja fikseerime poolis tekkiva induktsioonivoolu väärtuse. | Esimesest katsest võime järeldada, et suurem elektromotoorjõud tekib poolis siis, kui magnetinduktsioon pooli asukohas rohkem muutub. Täpsemad mõõtmised näitavad, et induktsiooni elektromotoorjõud on võrdeline suuruse B muutusega. Järelikult on elektromagnetilise induktsiooni nähtuse kirjeldamiseks vajalik suurus võrdeline magnetinduktsiooniga B. |
| Teisest katsest võime järeldada, et füüsikaline suurus, mille muutumine on vajalik elektromagnetilise induktsiooni tekkimiseks, peab olema (vähemasti ligikaudu) võrdeline pindalaga S, mida läbivad muutuva magnetvälja jõujooned. | Nagu näeme, sõltub induktsioonivool ja järelikult ka induktsiooni elektromotoorjõud nurgast β pooli telje ja muutuva magnetvälja suuna vahel. Seda sõltuvust kirjeldav nurgafunktsioon peab olema maksimaalne juhul, kui nurk on null. Ise peab see funktsioon aga nullistuma täisnurga korral |
Kõiki neid katseid võib läbi viia ka simulatsioonides. Viitame siin ühte sellist. Vaadake ja kontrollige, elu või simulatsiooni, teie valik.
Ülalkirjeldatud katsete tulemuste kokkuvõtlikuks esitamiseks on võetud kasutusele füüsikaline suurus nimega magnetvoog. Magnetvoog näitab, millisel määral läbivad magnetvälja jõujooned vaadeldavat pinda selle pinna suuruse ja asendi tõttu magnetväljas. Piltlikult öeldes näitab magnetvoog pinda läbivate jõujoonte arvu. Loomulikult on see arv eelkõige määratud jõujoonte tihedusega, mida teatavasti iseloomustab magnetinduktsioon. Mingit kindlat pinda läbib joonte suurema tiheduse korral rohkem jõujooni. Magnetvoog läbi vaadeldava pinna on võrdeline magnetinduktsiooniga . Samas läheb pinnast rohkem jõujooni läbi ka siis, kui pind ise on suurem ning jääb seetõttu jõujoontele rohkem "ette". Magnetvoog on võrdeline pinna pindalaga . Jõujoonte kindla tiheduse () ja pinna pindala () korral sõltub pinda läbiv magnetvoog B-vektori suunast pinna suhtes. Kui pind on -vektoriga risti (), siis läbib pinda suurim arv jõujooni (J.2.24, a). Sel korral on tegemist suurima magnetvooga. Kui nurk B-vektori ja pinna normaali vahel erineb nullist, siis on pinda läbivate jõujoonte arv väiksem (J.2.24, b). Seega on väiksem ka magnetvoog. Kui aga nurk on täisnurk (), siis on magnetvälja jõujooned pinnaga paralleelsed. Mitte ükski jõujoon ei läbi pinda. Magnetvoog on null (J.2.24, c). Magnetvoog on maksimaalne nulliga võrduva nurga korral ning saab ise nulliks, kui see nurk on täisnurk. Seega on magnetvoog võrdeline koosinusega nurgast magnetvälja suuna ja pinna normaali
Kõik ülaltoodu võib kokku võtta magnetvoo definitsioonivalemisse
Magnetvoog on skalaarne (suunata), kuid algebraline suurus. Magnetvoo algebralisus tähendab seda, et sõltuvalt magnetvälja suunast võib voog olla nii positiivne kui ka negatiivne suurus. Magnetvoo mõõtühikuks SI-süsteemis on üks veeber (). Üks veeber on magnetvoog, mis läbib 1 m2 suurust magnetvälja suunaga ristuvat pinda, kui välja magnetinduktsioon on . Ühe veebri defineerimisel kasutatakse niisiis valemi 2.5 erijuhtu, mil , seega ja järelikult , millest
Induktsioonivool ja ka vastav elektromotoorjõud %i on seda suuremad, mida kiiremini (s.t mida lühema ajavahemiku jooksul) magnetvälja muutus toimub. Kasutades magnetvoo mõistet, võib kõigi Faraday katsete tulemuse üldistada kujul
mis näitab, et induktsiooni elektromotoorjõud on võrdeline magnetvoo muutumise kiirusega. See ongi elektromagnetilise induktsiooni põhiseadus ehk lihtsalt Faraday induktsiooniseadus. Mõistagi on jutt magnetvoost läbi pinna, mis on piiratud vaadeldava juhtmekeeruga. Pooli korral liituvad üksikutes keerdudes tekkivad elektromotoorjõud. Siis tuleb magnetvoo all mõista voogu läbi summaarse keerdudest piiratud pinna ning arvestada ka keerdude magnetväljade vastastikust mõju. Miinusmärk näitab toimuva muutuse suunda.
| Induktsioonivoolud ei teki ainult laboritingimustes. Kui Päikeselt lähtuv, virmalisi tekitav elektrijuga (vool) ionosfääris tekitab muutuva magnetvoo läbi vertikaalse kontuuri, mille moodustavad elektriliinid, Maa pind ja transformaatorite maandusjuhtmed, indutseeritakse selles juhtivas kontuuris vool IGIV . Tugevad päikesetormid on sel kombel rivist välja löönud terveid elektrijaotussüsteeme. | Kui suur päikesetorm läheb maast napilt mööda. |
Võrdetegur sõltub mõõtühikute süsteemi valikust. SI-s ja järelikult
SI korral ei ole induktsiooni elektromotoorjõud mitte ainult võrdeline vaid lausa arvuliselt võrdne magnetvoo muutumise kiirusega. Ühikusüsteem SI ongi loodud nõnda, et elektromagnetilise induktsiooni seaduses võrdetegur puuduks. Just seetõttu ilmub selles süsteemis Coulomb'i seadusesse ühikut omav võrdetegur.
Kasutades Faraday induktsiooniseadust kujul 2.7 , võime magnetvoo ühiku defineerida seosest
Vastavalt on üks veeber selline magnetvoo muut, mis ühe sekundi jooksul toimudes tekitab induktsiooni elektromotoorjõu üks volt ().
Näide 2.2.
Papptorukesele keriti 400 keerust koosnev juhtmepool. Pooli otste külge ühendati voltmeetrina toimiv multimeeter ehk tester, mille takistuse võib lugeda pooli takistusega võrreldes lõpmata suureks. Seega toimis pool vooluallikana, mille EMJ oli praktiliselt võrdne testril tekkiva pingega. Kui pooli sisse pisteti 1 sekundi jooksul püsimagnet ristlõikepindalaga , siis hälbis testri osuti väärtuseni . Kui palju muutus magnetvoog ühes keerus? Kui suur on magnetinduktsioon selle püsimagneti sees?
Lahendus
Andmed
Arvutused:
Pooli keerud toimivad jadamisi ühendatud vooluallikatena, mille põhjal induktsiooni EMJ kogu poolis
kus – elektromotoorjõud ühes keerus ja – keerdude arv.
Faraday induktsiooniseadust
võime siin kasutada ilma miinusmärgita, sest meid huvitab vaid muutuse suurus, mitte suund.
Magnetvoo muut:
Kuna magnetvoo algväärtus on null, siis võrdub lõppväärtus muuduga . Püsimagneti magnetväli on paralleelne pooli teljega ning on seega suunatud piki keerdude ühist normaali. Järelikult , ja . Sellest
Vastus: Magnetvoog ühes keerus muutus 25 mikroveebri võrra. Püsimagneti magnetinduktsioon oli 0,5 teslat.
Lugedes veel kord Faraday katsete kirjeldusi punktis 2.3, märkame, et magnetvälja kasvu korral sisaldavad need hulgaliselt sõna vastupidine. Näiteks püsimagneti lähendamisel juhtmepoolile on induktsioonivoolu magnetväli vastassuunaline püsimagneti väljale, mis voolu esile kutsus. Induktsioonivoolu väli takistab magnetvälja kasvu. Poolis tekkiva induktsioonivoolu suund on vastupidine voolu suunale teises poolis, mida esimesele lähendatakse. Voolu sisselülitamine ühes juhtmes indutseerib vastupidise suunaga voolu naaberjuhtmes.
Magnetvälja kahanemise korral on aga kõik teisiti. Püsimagneti eemaldamisel poolist on induktsioonivoolu magnetväli samasuunaline püsimagneti väljaga ning takistab magnetvälja kahanemist. Juhtmepoolide eemaldamisel teineteisest on ühes poolis indutseeritav vool samasuunaline vooluga teises poolis. Voolu väljalülitamine ühes juhtmes indutseerib samasuunalise voolu naaberjuhtmes. Seega soodustab induktsioonivool alati olemasoleva olukorra säilimist.
Elektromagnetiline induktsioon on alalhoidlik ehk konservatiivne nähtus. Seda asjaolu märkas esimesena Emil Lenz (1804-1865), Tartust pärit Vene füüsik, rahvuselt baltisakslane. Kogu maailm tunnustab Emil Lenzi teeneid induktsioonivoolu suunda määrava reegli või seaduse formuleerijana. Seetõttu esinebki nimetatud seadus füüsikaõpikutes Lenzi reegli või Lenzi seaduse nime all.
Järgnevalt toome ära Lenzi reegli mõned sõnastused:
- induktsioonivoolu suund on selline, et tema magnetväli kompenseeriks muutust, mis voolu põhjustab;
- induktsioonivool toimib alati vastupidiselt seda voolu esile kutsuvale põhjusele;
- kui välismõju tingib magnetvoo kasvu kontuuris, siis on induktsioonivoolu magnetväli välise magnetvälja suhtes vastassuunaline (takistab kasvu). Kui aga välismõju põhjustab magnetvoo kahanemist, siis on induktsioonivoolu magnetväli välise magnetväljaga samasuunaline (takistab kahanemist).
Lenzi reegli levinuim sõnastus on (a), lühimaks võib pidada varianti (b), kõige üksikasjalikumaks aga võimalust (c).
Lenzi reegli analoogiks mehaanikas on väide, et stabiilsele süsteemile mõjuv jõud on suunatud tasakaaluasendi poole. Kui me viime näiteks pendli tasakaaluasendist välja, siis tekib otsekohe jõud , mis takistab niisugust muutust. See jõud püüab viia pendlit tagasi tasakaaluasendisse. Samamoodi on lood kuulikesega, mis asetseb nõgusa põhjaga kausis. Kuulikese väljaviimisel kausi madalaimast punktist tekib jõud, mis lükkab kuulikest tagasi tasakaaluasendisse, see tähendab, kausi põhja.
Mõnikord öeldakse ka, et Lenzi reegel väljendab energia jäävuse seadust. Kujutlegem, mis juhtuks siis, kui Lenzi reegel ei kehtiks ja mingist muutusest tingitud induktsioonivool soodustaks muutuse jätkumist. Näiteks püsimagneti lähendamisel juhtmepoolile tekiks poolis sel juhul vool, mille magnetväli oleks püsimagneti väljaga samasuunaline. Poolile mõjuv magnetväli tugevneks ja "tagurpidise" Lenzi reegli kohaselt kasvaks vool seeläbi veelgi. Voolu suurenemine põhjustaks selle kasvu üha kiiremat jätkumist. Tegemist oleks eimillegi arvelt töötava vooluallikaga, niisiis perpetuum mobile'ga. Niisugust masinat ei saa aga energia jäävuse seaduse kohaselt olemas olla.
Lenzi reeglit väljendab induktsiooniseaduses (valemis 2.9) sisalduv miinusmärk. Kui näiteks juhtmekeerdu läbiv magnetvoog kasvab ( valemis 2.9), siis loetakse induktsiooni elektromotoorjõudu ja vastavat voolutugevust kokkuleppeliselt negatiivseteks, kuna induktsioonivoolu magnetväli on keerus mõjuvale väljale vastassuunaline (takistab magnetvoo kasvu). Kui aga magnetvoog juhtmekeerus kahaneb ja tema muut on negatiivne (), siis on need kaks välja samasuunalised.
Induktsioonivool püüab kahanevat magnetvoogu alal hoida. Seetõttu loetakse induktsiooni elektromotoorjõudu ja voolutugevust positiivseteks.
| Selles kuulsas 2006.a. Massachusetsi Tehnoloogiainstituudis tehtud eksperimendis pandi elektromagnetväljade tekitatud induktsioonivooludega tööle 60W elektripirn. Täna on sellised seadmed reaalselt saadaval, näiteks oma mobiiltelefoni saame me laadida ilma, et sellele ühtki juhet kinnitama peaks. | Elektriautod ei suuda ilma laadimata sõita Tartust Tallinnasse. Ühe lahendusena võib välja pakkuda akude laadimist induktsioonivoolude abil. Teekattesse monteeritud poolide magnetväli kutsub esile induktsioonivoolud neist üle sõitvate autode analoogilistes poolides, mida siis kasutatakse elektriauto akude laadimiseks. Nende küsimustega tegeleme täpsemalt Energia kursuses. |
Kui me oleme eespool (p.2.3.1) kirjeldatud viisil valmistanud raudsüdamikuga juhtmepooli, siis saame Lenzi reegli kehtivust üpris lihtsalt kontrollida. Selleks püüame leida vasest, hõbedast või alumiiniumist rõnga, millest kasutatava pooli südamik (raudpolt) takerdumata läbi mahub. Hästi sobib näiteks kerge hõbesõrmus. Paigutame raudsüdamikuga juhtmepooli laual mingile alusele, nii et südamik ulatuks poolist paari sentimeetri pikkuselt välja. Paneme metallrõnga kahe niidiga laualambi või mingi muu raami külge rippuma. Seejuures peab raudsüdamik ulatuma rõnga sisse. Kui me nüüd tekitame südamikuga poolis taskulambipatarei abil voolu, siis nihkub rõngas poolist eemale, kuna rõngas tekkiv induktsioonivool takistab Lenzi reegli kohaselt poolist pärineva magnetvoo kasvu. Seetõttu on induktsioonivool rõngas pooli voolule vastassuunaline (J.2.25, a), vastandlike suundadega voolud aga tõukuvad (p.1.4.2). Loomulikult ei jää rõngas ,,eemaletõukunud“ asendisse. Kui pooli magnetväli enam ei kasva, siis langeb induktsioonivoolu tugevus nullini ja rõngas naaseb raskusjõu mõjul tasakaaluasendisse. Kui me nüüd poolis voolu katkestame (eemaldame patarei), siis poolist pärinev magnetvoog kahaneb. Induktsioonivoolu magnetväli üritab seda aga Lenzi reegli kohaselt alal hoida (takistab kahanemist). Nüüd on voolude magnetväljad ja seega ka voolud ise samasuunalised (J.2.25, b). Samasuunalised voolud aga tõmbuvad. Seetõttu nihkub rõngas pooli poole. Kui poolist pärinev magnetvoog on saanud nulliks (enam ei kahane), siis induktsioonivool katkeb ja rõngas naaseb jällegi raskusjõu mõjul tasakaaluasendisse.
Ülalkirjeldatud viisil tekivad induktsioonivoolud mitte ainult rippuvas rõngas, vaid ka suvalise kujuga metallkehas, millele mõjuv magnetväli piisavalt kiiresti muutub. Selliseid voolusid nimetatakse pöörisvooludeks, kuna neid tekitab elektromagnetilisel induktsioonil esinev pööriselektriväli. Kui mingi metallkeha magnetväljas liigub, siis pöörisvoolude olemasolu pidurdab seda liikumist. Keha kui terviku liikumise kineetiline energia läheb üle laengukandjate liikumise energiaks selles kehas.
Võib ka öelda, et laengukandjad liiguvad pööriselektrivälja energia arvel. Elektritakistuse olemasolu tõttu eraldub see energia aga soojusena. Kineetiline energia muundub soojuseks nii nagu tavalisel hõõrdumisel.
| Pöörisvooludel põhineb ka induktsiooniahju töö. See seade võimaldab kiiresti kuumutada elektrit juhtivat ainet. Suure sagedusega perioodiliselt muutuva magnetvälja abil tekitatakse aines pöörisvoolud, mille energia vabaneb soojusena. Induktsiooniahju korral ei toimu soojusülekannet ühelt kehalt teisele. Soojus eraldub sellessamas aines, mida kuumutatakse. Seetõttu on induktsiooniahjul väga kõrge kasutegur. | Siin pildil kujutatud eksperimendis pöörlevad kaks vasest silindrit kiiresti vastassuundades. Silindrite peale asetati tugev magnet, nii et silindrite pööreldes indutseeritakse seal tugevad induktsioonivoolud. Need pöörisvoolud püüavad Lenzi reegli kohaselt elimineerida kiiresti muutuvat magnetvälja, tekitades vastassuunalise magnetvälja. Tulemus on pildil näha - magnet jääb silindrite kohale õhku "rippuma". |
Oleme juba korduvalt täheldanud induktsiooni elektromotoorjõu tekkimist poolis, mille keerde läbivat magnetvoogu väljastpoolt muudetakse. Näiteks katsetes kahe pooliga (p.2.4.1) toimub see teises poolis voolu sisse- või väljalülitamise teel. Kuid ka magnetvälja tekitavas poolis esineb voolu kasvul või kahanemisel magnetvoo muutus. See muutus tekitab induktsiooni elektromotoorjõu, mis Lenzi reegli kohaselt takistab muutust ning järelikult pidurdab voolu kasvu või kahanemist. Niisiis võib juhtmes induktsiooni elektromotoorjõu tekkimiseks vajalik magnetvoo muutus olla põhjustatud ka voolu muutumisest juhtmes endas. Elektromagnetilise induktsiooni nähtuse sellist alaliiki nimetatakse endainduktsiooniks.
Endainduktsiooni olemasolu kindlakstegemiseks võib kasutada Faraday katsete (p.2.3) korraldamiseks valmistatud pooli. Ühendame südamikuta pooli otste külge uue lapiku taskulambipatarei. Kui me voolu ahelas katkestame, siis kuuleme praksatust ja märkame katkestuskohas nõrka elektrisädet. Säde on paremini jälgitav, kui teeme katset hämaras või koguni pimedas toas.
Järelikult tekib ahelas voolu katkestamisel täiendav pinge, mis püüab voolu säilitada.
Tekkiv pinge rakendub katkestuskohas, sest just seda kohta on liikuvatel laengukandjatel kõige raskem läbida. Seal tuleb teha kõige rohkem tööd. Paigutame nüüd pooli sisse raudpoldi ja kordame katset. Näeme, et tekkiv säde on oluliselt tugevam. Vahemik, milles õhk hakkab elektrit juhtima, on tunduvalt laiem.
Arvestame, et sädelahendus tekib õhus ühe kindla elektrivälja tugevuse juures ().
Konstantsel väljatugevusel E on kahe punkti vaheline pinge aga seda kõrgem, mida suurem on nende punktide vahekaugus (valem ). Seega tekib raudsüdamikuga pooli korral suurem pinge.
Kuna just raudsüdamikuga poolis tekib suurem magnet-induktsioon, siis võib väita, et see pinge sõltub magnetinduktsioonist poolis või pooli keerde läbivast magnetvoost. Pool hakkab voolu muutumisel toimima vooluallikana, mille elektromotoorjõudu nimetatakse endainduktsiooni elektromotoorjõuks. Vooluringi sulgemisel on pooli kui vooluallika polaarsus patarei omale vastupidine (J.2.27, pool takistab voolu kasvu). Vooluringi katkestamisel aga on pool ja patarei ühesuguse polaarsusega (pool püüab voolu alal hoida).
Katsest 2.5 näeme, et endainduktsiooni nähtus avaldub inertsina laetud osakeste suunatud liikumisele. Endainduktsiooni esinemise korral võtab elektrivoolu tekitamine ja ka peatamine oluliselt rohkem aega võrreldes juhuga, mil endainduktsioon puudub. Tulemus näitab, et sädet tekitav pinge on (vähemasti osaliselt) põhjustatud voolu katkestamisest poolis. Vool raudsüdamikuga pooli sisaldavas ahelas käitub nagu raske raudteerong. Sellist rongi ei saa hetkeliselt liikuma panna ega ka järsult peatada. Palju kuuldud kurvad lood õnnetustest raudteeületuskohtadel ongi ju õigupoolest selle tagajärg, et rasket rongi pole võimalik hetkeliselt seisma jätta. Kuid miks vool mõnes ahelas käitub raske rongina, mõnes aga mitte? Millal esineb endainduktsioon? Ka nendele küsimustele annab vastuse äsja korraldatud katse. Endainduktsiooni tekkimiseks peab vooluga kaasnema tugev magnetväli, mis suudab samas mõjutada ka voolu ennast. Täpsemalt öeldes peab vool vaadeldavas juhtmesüsteemis tekitama suure magnetvoo, sest just magnetvoo muutumine kutsub esile induktsiooni elektromotoorjõu. Raudsüdamikuga juhtmepooli korral on magnetvoog oluliselt suurem kui tühjas poolis.
Seega on endainduktsiooni esinemine määratud voolu suutlikkusega tekitada antud juhtmesüsteemis magnetvoogu. Juhtmesüsteemi vastavate omaduste kirjeldamiseks on kasutusel füüsikaline suurus, mida nimetatakse juhi induktiivsuseks.
Ülalpool kirjeldatud katse käigus tekkis raudsüdamikuga pooli sisaldavas vooluringis suur endainduktsiooni elektromotoorjõud. Raudsüdamiku puudumisel oli see aga väiksem. Näeme, et juhi (või vooluringi osa) induktiivsust võib määratleda mingil kindlal voolu muutusel tekkiva endainduktsiooni elektromotoorjõu kaudu. Juhi induktiivsus näitab, kui suur endainduktsiooni elektromotoorjõud tekib selles juhis voolutugevuse ühikulisel muutumisel ajaühiku jooksul
Absoluutväärtuse märk selles valemis näitab, et induktiivsust vaadeldakse kokkuleppeliselt vaid positiivse suurusena. Voolutugevuse muut ja endainduktsiooni elektromotoorjõud võivad aga olla ka negatiivsed. Siin ja allpool asume kasutama elektromagnetismi füüsikas üldlevinud kokkulepet, mille kohaselt mingit kindlat või konstantset laengut, pinget, voolutugevust vms elektrilist suurust tähistatakse suurtähtedega (, , ), vastavaid ajas muutuvaid suurusi aga väiketähtedega (, , ). Kuna induktiivsuse mõiste eeldab olemuslikult voolu muutumist ajas, siis on korrektne tähistada voolutugevust väiketähega (). Voolutugevuse muudu ja sellele vastava ajavahemiku suhet valemis 2.8 võib nimetada voolu muutumise kiiruseks. Seega näitab juhi induktiivsus meile, kui suur endainduktsiooni elektromotoorjõud tekib selles juhis, kui voolutugevus temas muutub ühikulise kiirusega.
Avaldades valemist 2.8 endainduktsiooni elektromotoorjõu ning kasutades Lenzi reeglit väljendavat miinusmärki, saame
Võrdleme nüüd valemit 2.9 Faraday induktsiooniseadusega (valem 2.7). Seejuures arvestame, et endainduktsioon on elektromagnetilise induktsiooni erijuht, mistõttu ja 2.9 esinevate murdude väärtused ja seega ka nende murdude lugejad on võrdsed:
ehk
Juhi induktiivsus näitab meile, kui suure magnetvoo muutuse tekitab selle juhi korral ühikuline voolu muutus. Veelgi lihtsamalt öeldes näitab induktiivsus vaadeldava juhtmesüsteemi inertsust temas toimuvate voolu muutuste suhtes.
Endainduktsiooni elektromotoorjõu sõltuvuse voolu muutumise kiirusest avastas aastal 1832 Ameerika füüsik Joseph Henry (1797 – 1878). Seetõttu on valem 2.9 ka tuntud Henry seaduse nime all. Kuna Henry jõudis induktsiooniseaduseni Faraday'st sõltumatult, siis nimetatakse elektromagnetilise induktsiooni seadust mõnikord ka Faraday-Henry seaduseks. J. Henry järgi on oma nime saanud induktiivsuse SI-ühik henri (). Valemite 2.8 ja 2.10 põhjal
Induktiivsuse definitsioonina võib vaadelda nii valemit 2.8 kui ka valemit 2.10. Paraku peitub valemis 2.10 tema välisele lihtsusele vaatamata väärtõlgenduse oht. Nimelt on seal sisalduv magnetvoog valemi 2.6 abil leitav vaid ühe juhtmekeeru korral. Juhtmepooli keerud aga tugevdavad vastastikku üksteise magnetvälja. Resultantvälja jõujooned läbivad pooli kõiki keerde. Magnetinduktsioon poolis ja seega ka magnetvoog läbi keerdude on seda suuremad, mida rohkem keerde on poolil pikkusühiku kohta. Vastavalt on sel juhul suurem ka pooli induktiivsus. Valemis 2.10 esinevat magnetvoogu nimetatakse siis pooli kogumagnetvooks ehk aheldusvooks ja selle suuruse väljaarvutamine on üldjuhul keeruline protseduur.
Peagi (p2.7.2) veendume selles, et induktiivsus kirjeldab kehade süsteemi võimet säilitada endas elektrivoolu ja seeläbi tekitada magnetvälja. Mõistagi on kasutusel ka füüsikaline suurus, mis iseloomustab kehade süsteemi võimet salvestada endasse laengut ja seeläbi tekitada elektrivälja. Kõnealuseks suuruseks on elektrimahtuvus, mida me edaspidi nimetame lihtsalt mahtuvuseks.
Kallates vedelikku ühekõrgustesse kuid erineva läbimõõduga klaasidesse, näeme otsekohe, et laiemasse klaasi mahub rohkem vedelikku. Suurema läbimõõduga anumal on suurem põhja pindala ja seega ka ruumala (J.2.28). Samamoodi on lood erinevate elektrit juhtivate kehade laadimisel. Ühele kehale "mahub" rohkem laengut kui teisele. Järelikult on mõtet võtta kasutusele keha laadumisvõimet kirjeldav suurus, mida nimetatakse keha mahtuvuseks.
Rangelt võttes on mahtuvus alati kahe keha omavaheline mahtuvus. Andes ühele kehale mingi laengu, peame selle mingilt teiselt kehalt ära võtma, kuna kehtib laengu jäävuse seadus.
Vaatleme kahte algselt neutraalset keha. Kui me võtame ühelt kehalt ära laengu ja anname selle teisele kehale, siis omandab esimene keha laengu ja teine . Kehade vahel tekib elektriväli ja seega ka potentsiaalide vahe (pinge) (J.2.29). Kuna potentsiaal on võrdeline teda tekitava laenguga (valem 1.22), siis teostades sama toimingu laenguga , tekitame kehade vahel pinge . Peagi märkame, et laengu ja pinge jagatis jääb kõigis sellelaadsetes katsetes muutumatuks, antud kehade süsteemi iseloomustavaks suuruseks. See ongi vaadeldavate kehade omavaheline mahtuvus.
Kahe keha omavaheline mahtuvus näitab, kui suure laengu viimisel ühelt kehalt teisele tekib kehade vahel ühikuline pinge. Mahtuvuse leidmiseks tuleb üle viidud laeng jagada tekkiva pingega
Saavutamaks mahtuvuse definitsiooni suuremat sarnasust induktiivsuse määratlusega (2.10) ja rõhutamaks ajalise muutuse tähtsust võib üleviidavat laengut Q vaadelda keha laengu lõppväärtuse ja algväärtuse vahena: . Siis on keha iseloomustav laeng meile mehaanikast tuntud koordinaadi rollis ja üleviidav laeng vastab kahe koordinaadi vahele ehk teepikkusele. Vaadeldes keha laengut ajast sõltuva suurusena , peame ajast sõltuvana käsitlema ka kahe keha vahel tekkivat pinget . Niimoodi võtab kahe keha omavahelise mahtuvuse definitsioon kuju
Nüüd saab meile selgeks elektriseadmete kaitsemaanduse põhimõte, millest oli juttu juba põhikooli Elektriõpetuses. Maandamisel ühendatakse seadme metallkorpus juhtme abil Maaga. See kaitseb seadme kasutajat elektrilöögi eest juhul, kui seadme korpus satub rikke tagajärjel Maa suhtes pinge alla. Kaitsemaandus juhib seadme korpusele sattunud laengu ära Maasse. Maa on aga niivõrd suure mahtuvusega keha, et talle võib anda kuitahes suure laengu, ilma et tema potentsiaal märgatavalt muutuks. Laeng liigub Maasse läbi maandusjuhtme, mitte aga läbi seadme kasutaja keha. Seega on mingi keha maandamine samaväärne suure augu tegemisega niisuguse anuma põhja, millesse vesi mitte mingil juhul koguneda ei tohi. Kui ka vesi eksikombel satub anumasse, jookseb vesi läbi augu otsekohe maha.
Kehade süsteemi, mis on loodud mingi kindla mahtuvuse saamiseks, nimetatakse kondensaatoriks. Lihtsaim kondensaator koosneb kahest elektrit juhtivast plaadist ehk kattest, mille vahel paikneb dielektrikukiht. Kondensaatori mahtuvus näitab, kui suure laengu andmisel ühele plaadile suureneb plaatidevaheline pinge ühe ühiku võrra. Seega on kondensaatori mahtuvus sisuliselt tema plaatide omavaheline mahtuvus (valem 2.12 või 2.13).
Kondensaatori laadimiseks reeglina ei võeta laengut ühelt plaadilt, et anda seda teisele plaadile. Piisab vaid ühe plaadi laadimisest. Laetud plaadi elektrivälja mõjul hakkavad laengukandjad teisel plaadil ja sellega ühendatud juhtides liikuma. Näiteks laengu andmisel kondensaatori ühele plaadile omandab teine (algselt neutraalne) plaat sama suure laengu , sest just siis tasakaalustavad plaatide elektriväljad väljaspool kondensaatorit vastastikku teineteist. Samanimeliste laengute tõukumise tõttu lahkub laeng teiselt plaadilt. Laengu saab kergesti teisele plaadile tuua siis, kui plaat on maandatud (J.2.30) ja laeng võib lahkuda Maasse.
Ka vooluringis paikneva kondensaatori korral saab laeng teiselt plaadilt alati ära minna. Järelikult on ühe plaadi laadimine samaväärne laengu üleviimisega ühelt plaadilt teisele.
Mahtuvuse ühik SI-süsteemis kannab M. Faraday auks nime farad. Üks farad () on sellise keha mahtuvus, millele tuleb anda laeng üks kulon, selleks et suurendada tema potentsiaali ühe voldi võrra. Kondensaatori mahtuvus on , kui laengu viimine ühelt plaadilt teisele tekitab plaatide vahel pinge . Seega
Kuna üks kulon on väga suur laeng, siis ka üks farad on väga suur mahtuvus. Seetõttu kasutatakse praktikas enamasti mikro-, nano- ja pikofaradeid (, , ).
Kondensaatoreid võib leida kõikvõimalikes elektroonikaseadmetes, alustades mikrofonidest ning lõpetades näiteks satelliitidega. Esimese kondensaatori valmistasid teineteisest sõltumatult sakslane Ewald von Kleist (1700-1748) ja hollandlane Pieter van Musschenbroek (1692-1761). Kondensaatori leiutamist on õigem nimetada avastuseks, sest see toimus täiesti juhuslikult. Uurides vee elektriseerumist, tegi Kleist 1745. aastal järgmise katse. Ta laadis raudnaela, mis ulatus välja veega täidetud klaaspudelist. Hoides pudelit ühes käes, puudutas ta kogemata teise käega naela ja sai er akordselt tugeva elektrilöögi. Kleist mõistis, et pudelisse oli kogunenud väga suur laeng. Pudelkondensaatori üheks katteks oli vesi, teiseks aga katsetaja käsi. Pudeli klaaskest toimis dielektrikuna.
| J.2.32 Pudelkondensaator. Tavaline limonaadipudel on täidetud soolveega, pudeli korgist on läbi pandud polt, mille ots ulatub soolvette. Pudeli välisküljele on liimitud fooliumiriba. Sellist kondensaatorit saab laadida näiteks elektrofoormasinaga. Ettevaatust, kondensaatorist saadav "särts" võib olla üsnagi tuntav! | Kui purgi sisemisele ja välimisele küljele kinnitada kaks alumiiniumfooliumi lehte, käitub see seade kondensaatorina. Tuntakse ka Leideni purgi nime all. |
Analoogilise katse teostas Musschenbroek 1746. a. hollandi linnas Leidenis. Kuna laiemalt tuntuks sai just nimelt tema tulemus, siis hakati kõiki sellelaadseid laengut koguvaid klaasanumaid nimetama leideni purkideks.
Leideni purgi konstruktsioonis asendati vesi peagi anuma sisepinda katva metallkilega. Ka välimine kate valmistati metallfooliumist. Nii saadi leideni purk, mis on kooli füüsikakabinetis kasutusel tänapäevani.
Endainduktsioon
Endainduktsiooni nähtuseks nimetatakse elektromagnetilise induktsiooni alaliiki, mille korral magnetvoo muutus on põhjustatud voolu muutusest vaadeldavas juhtmes endas.
Juhi induktiivsus
Juhi induktiivsus näitab, kui suur endainduktsiooni elektromotoorjõud tekib selles juhis voolutugevuse ühikulisel muutumisel ajaühiku jooksul. Induktiivsus näitab ühtlasi kogumagnetvoo muutust juhis juhti läbiva voolu tugevuse ühikulisel muutumisel.
Kahe keha omavaheline mahtuvus
Kahe keha omavaheline mahtuvus näitab, kui suure laengu viimine ühelt kehalt teisele tekitab kehade vahel ühikulise pinge.
Keha mahtuvus
Keha mahtuvus näitab, kui suure laengu andmisel kehale tekib keha potentsiaali ühikuline muutus.
Elektrivälja olemasolu tähendab teatavasti jõu tekkimise võimalikkust. Analoogiliselt väljendab termin elektrivälja energia seda, et laetud keha võib elektriväljas omada energiat. Asume uurima, kuidas sõltub elektrivälja energia väljatugevusest või potentsiaalist. Kõige lihtsam on seda teha homogeense välja korral, mis täidab kondensaatori plaatide vahelist ruumi.
| Suure mahtuvusega kondensaator lühistamine metallvardaga. Tugev valgussähvatus (säde) ja sellega kaasnev pauk näitavad suure energia eraldumist. See on kondensaatoris salvestatud elektrivälja energia. Kondensaaatori mahtuvus on 300 mF ja see laeti pingeni 700 V. | Suure mahtuvusega kondensaatori lühistamine läbi arbuusi. Arbuusil ei lähe hästi. |
Energia olemasolu laetud kondensaatoril pole raske näidata. Kondensaatori lühistamisel tekkiv säde võib olla välguna ere ning kostev pauk kõrvulukustav. Suure mahtuvusega kondensaatori tühjendamist läbi oma keha ei tasu südamehaigetel ja nõrganärvilistel üldse proovida.
Laetud kondensaatori energia on aga tegelikult tema plaatide vahelist ruumi täitva elektrivälja energia. Paremini mõistame seda siis, kui arvestame, et laetud kondensaator sarnaneb kõrge täidetud veenõuga. Avades nõu põhjas oleva kraani, tekitame veejoa. Juga suudab teha tööd, näiteks panna liikuma vesiratta. Seda tööd tehakse mitte veenõu, vaid vee raskusjõu potentsiaalse energia arvelt. Viimane on aga oma sügavamalt olemuselt Maa gravitatsioonivälja energia. Täpselt niisamuti ei tee tööd mitte kondensaator, vaid temas sisalduv elektriväli.
Laetud kondensaator suudab teha tööd tänu sellele, et tööd on tehtud ka tema laadimisel. Kuna katetevaheline pinge muutub laadimise käigus, siis ei saa me tehtavat tööd otsekohe leida valemist 1.23
sest me ei tea, missugust pinget kasutada. Mida suurem on kondensaatori katetele juba kogunenud laeng, seda suurem on pinge plaatide vahel ja seda rohkem tuleb kondensaatori täiendaval laadimisel tööd teha.
Selleks et leida kogu tööd, mis tehakse kondensaatori laadimisel, tuleb katetele antud laengut korrutada mitte pinge lõppväärtusega , vaid laadimisel esineva keskmise pingega. Pinge kondensaatoril kasvab võrdeliselt laenguga alates nullist kuni lõppväärtuseni . Keskmine pinge kui pool algväärtuse ja lõppväärtuse summast on seega . Laadimisel tehtud töö või kondensaatoris tekitatud elektrivälja energia avaldub kujul
kus kogulaeng on mahtuvuse definitsiooni põhjal asendatud korrutisega ning pinge rollis esineb laadimisprotsessi keskmine pinge .
Oleme leidnud kondensaatori elektrivälja energia sõltuvuse plaatidevahelisest pingest ehk ühe plaadi potentsiaalist teise suhtes. Selle energia võib avaldada ka väljatugevuse kaudu. Kuna
siis plaatide kindla vahekauguse korral on pinge ja väljatugevus omavahel võrdelised. Seega on elektrivälja energia võrdeline ka väljatugevuse ruuduga.
Oleme juba märkinud, et induktiivsuse osa magnetvälja füüsikas sarnaneb mahtuvuse rolliga elektrivälja käsitlemisel. Mõlemad suurused kirjeldavad mingi keha omadusi. Mahtuvus näitab, kui suur on kondensaatori laengu muutus katetevahelise pinge ühikulisel muutumisel, induktiivsus aga näitab, kui suur on magnetvoo muutus juhtmepoolis, kui seda pooli läbiva voolu tugevust ühiku võrra muudetakse.
Kondensaatori ja pooli rollide sarnasuse põhjal on alust arvata, et energiat ei oma mitte ainult laetud kondensaator vaid ka vooluga pool. Samale järeldusele viib meid katse 2.5 punktis 2.6.1. Voolu katkestamine poolis muudab pooli vooluallikaks, mis muundab voolu magnetvälja energiat elektrienergiaks. Just nimelt magnetvälja nõrgenemisel tekib ju voolu (ja seega ka magnetvälja) säilitada püüdev induktsiooni elektromotoorjõud.
Kondensaatoris salvestunud energia sõltub mahtuvusest. Seega võib oodata poolis salvestunud energia samalaadset sõltuvust pooli induktiivsusest. Kuna selle sõltuvuse kuju korrektne tuletamine nõuaks kõrgema matemaatika rakendamist, siis rajame lihtsama käsitluse uuritava elektrinähtuse sarnasusele mingi tuntud mehaanikanähtusega. Teades, et energia on vaid vooluga poolil, võime seostada pooli energiat liikuvate laengukandjate kineetilise energiaga. Mehaanikast hästi tuntud kineetilise energia avaldis
sisaldab keha kiiruse ruutu. Pooli energia valemis peaks sama rolli mängima suurus, mis on võrdeline laengukandjate suunatud liikumise keskmise kiirusega ning määrab ka otseselt pooli poolt tekitatava magnetvoo. Selliseks suuruseks on voolutugevus. Vooluga pooli energia peaks olema võrdeline voolutugevuse ruuduga.
Kineetilise energia avaldises sisaldub aga ka keha mass. Mass kirjeldab keha inertsust kiiruse muutuste suhtes. Mida suurem on mass, seda rohkem aega kulub keha kiiruse muutmiseks. Näiteks võib kiirusega 5 m/s liikuva lapsevankri peatada hetkeliselt. Raske rongi pidurdusteekond on sama kiiruse korral aga juba kümmekond meetrit pikk ja pidurdamine kestab vastavalt kauem.
Juhtmesüsteemi inertsust voolu muutuste suhtes kirjeldab induktiivsus. Seega täidab induktiivsus elektrilaengu liikumisel sama rolli, mida mass mehaanilise liikumise juures. Juhtmepooli energia avaldise koostamisel tuleb kineetilise energia valemis sisalduv mass asendada induktiivsusega. Ühtekokku saame vooluga juhtmepooli energia jaoks valemi
Vooluga pooli energiat võib nimetada magnetvälja energiaks (sellest ka tähis Em). Pooli energia on ju olemas tänu sellele, et pooli juhtmes liikuvatele laengukandjatele mõjub pooli enda magnetväli. Magnetvälja energia all mõtleme me energiat, mida selles väljas omaks magnetiliselt aktiivne keha.
Kuidas aga sõltub magnetvälja energia magnetinduktsioonist? Teatavasti (valem 1.15 p.1.5.3) on voolutugevus juhtmes ning juhtme poolt tekitatav magnetinduktsioon võrdelised. Kui vooluga pooli magnetvälja energia on võrdeline voolutugevuse ruuduga, siis on ta järelikult võrdeline ka magnetinduktsiooni ruuduga. Võime järeldada, et nii elektri- kui ka magnetnähtustes on välja energia võrdeline välja jõuparameetri (E või B) ruuduga. See väide kehtib elektromagnetvälja kohta tervikuna.
Energeetilises aspektis võime elektromagnetvälja elektri- ja magnetkomponenti kokkuvõtteks võrrelda järgmiselt.
Elektriväli | Magnetväli |
Kehade süsteemi võimet tekitada elektrivälja (salvestada laengut) kirjeldab mahtuvus selle SI-ühik on farad | Juhtmesüsteemi võimet tekitada magnetvälja (salvestada voolu) kirjeldab induktiivus selle SI-ühik on henri |
Kondensaator on kehade süsteem, mis on loodud kindla mahtuvuse saamiseks | Induktiivpool on juhtmesüsteem, mis on loodud kindla induktiivsuse saamiseks |
Elektrivälja energia kondensaatoris | Magnetvälja energia induktiivpoolis |
Juba avapildis näidatud MagLev rongi olemasolu tõestab, et elektromagnetiline levitatsioon on võimalik. Siin on aga suuri probleeme.
Esiteks, magnetid tõepoolest ei saa üksteise peal õhus hõljuda, kui palju me nendega ka ei katsetaks (vt ka J.2.34). Nii et tuleb olla kavalam. Võimalusi on mitmeid:
On võimalik ehitada selline magnetite süsteem, mille kohal magnet vurrina pööreldes stabiilselt hõljuma jääb (J.2.35). Aga kõik, kes on üritanud sellist vurri hõljuma saada võivad kinnitada, et see ei ole lihtne.
Esemeid on võimalik märksa stabiilsemalt leviteerima panna, kui asendame püsimagnetid elektromagnetitega ning muudame neid läbivat voolu suuremaks või väiksemaks vastavalt sellele, kas ese on oma soovitud asendist ühele või teisele poole kaldunud. Niimoodi töötab peatüki avalehe fotol olev maakera.
Teeme nüüd ühe mõttelise eksperimendi. Asetame mittemagneetuva elektrijuhi (so elektrijuhi, mis ei tõmbu magneti külge) magneti kohale. Mis juhtub, kui me hakkame seda elektrijuhti magnetitele lähemale nihutama? Lenzi reegel ütleb, et juhis tekivad voolud, mis üritavad magnetvälja muutumise mõju kompenseerida. Juhi ümber tekib püsimagnetile iseloomulik magnetväli, mis üritab juhti tagasi ülespoole lükata. Mida suurem muutus seda suuremad on induktsioonivoolud ja vastav tõukejõud. Elektrijuht peaks siis magneti kohale hõljuma jääma? Miks tavaelus näiteks vasest rõngas neist vooludest välja ei tee ja alla kukub? Põhjus on lihtne – elektrilise takistuse tõttu kustuvad tekkinud induktsioonivoolud väga kiiresti. Aga kui sellist elektrilist takistust ei esineks?
Selgub, et paljud ained muutuvad väga madalatel temperatuuridel ülijuhtideks, elekter liigub neis siis ilma igasuguse takistuseta. Sel juhul kirjeldatud mõtteline eksperiment töötab ka reaalselt – magnetite kohal ülijuhtivasse olekusse viidud juht jääb sinna hõljuma (vt J.2.36).
Nii et Tallinnast Tartu hõljuva rongi ehitamine on põhimõtteliselt lihtne – tuleb võtta diiselrong, eemaldada sellelt rattad, asendada mootor väga suure ülijuhiga, panna ülijuhid ka vagunitesse, asendada siis rööpad tugevate magnetite reaga (vt J.2.36), tõsta rong uuesti rööbaste kohale, jahutada need vedela lämmastiku temperatuurini (-195 kraadi), eemaldada toed ... ja kui me oleme kõige õigesti teinud, siis jääb rong oma magnetrööbaste kohale hõljuma. Aga kuidas selline rong edasi liikuda võiks? Ja pidurdada? Üks variant on paluda reisijatel korraks maha minna ja rongile hoog sisse lükata? Täiesti võimalik, sest selline rong liiguks ilma takistuseta ... aga mägisel maastikul ei pruugi see olla kõige parem mõte. Paneme vedurisse diiselmootori tagasi, rattad ka uuesti alla ning magnetite kõrvale rööpad ning kasutame seda vanamoodsat süsteemi rongi kiirendamiseks ja aeglustamiseks? Palistada magnetrada elektromagnetitega, mis lülitatakse sisse, kui rong läheneb ja välja, kui rong möödunud on ning mis tõmbavad rongi edasi?
Tulevik näitab, kas elektromagnetiline levitatsioon ka laiemat rakendust leiab. See on küll üsna kindel, et elektriautod tulevikus ikka ratastel sõidavad - magnetrööbaste ehitamine on ikka väga kallis lõbu. Pealegi on tänapäevased rongid võimelised ka rööbastel väga kiiresti sõitma.
Ja kas meil üldse on vaja mööda maad selliste kolossaalsete kiirustega sõita?
3D kinoga me oleme ära harjunud, paneme spetsiaalsed prillid ette ning ühtäkki omandab muidu lame kinolina sügavuse.
Tegelikult meile muidugi meeldiks nautida sellist elamust ilma, et peaksime end selleks prillidega ehtima. Niisamuti ei oleks meil midagi selle vastu, kui meie arvutiprojektorid suudaksid kuvada ruumilisi pilte. Ja arvatavasti ei oleks meil midagi selle vastu, kui meie telefonid saaksid hakkama sellega, mis näha parempoolsel pildil?
Küllap teavad seda ka need, kes filme, projektoreid ja telefone toodavad. Milles siis asi?
Elektromagnetvälja ühtse teooria lõi Faraday katsetulemuste põhjal šoti füüsik James Clerk Maxwell. Faraday oli veenvalt näidanud, et magnetvälja muutumisel tekib pööris-elektriväli sõltumatult muutuse päritolust. Maxwell oletas, et elektrivälja muutumine põhjustab samamoodi muutuva magnetvälja tekkimise, sõltumatult muutuva elektrivälja päritolust. Maxwelli käsitluse kohaselt jõuab elektrivälja muutus ühest ruumi punktist teise magnetvälja vahendusel. Elektrivälja muutumine ühes punktis põhjustab kõigepealt muutuva magnetvälja ja selle magnetvälja muutus kutsub elektromagnetilise induktsiooni teel esile elektrivälja muutumise naaberpunktis. See tähendab, et igasugune elektri- või magnetvälja muutus levib ruumis lainena. Just lainele on ju omane kindlate hälbeseisundite järjestikune esinemine laine levikusuunal paiknevates punktides. Tekkivat lainet nimetas Maxwell elektromagnetlaineks.
Püüame nüüd joonise 3.1 abil mõista elektromagnetlainete tekkemehhanismi. Lähenegu joonise ülemise vasaku nurga poolt vaatlejale X kiirusega liikuv positiivselt laetud keha. Täheldame, et selline liikumine on samaväärne vaatleja X poole kulgeva vooluga joonisel kujutatud juhtmes. Vaatleja X registreerib tema poole suunatud elektrivälja , sest tegemist on positiivse laenguga. See väli tugevneb, kuna välja tekitav keha läheneb vaatlejale, väljatugevus aga on teatavasti pöördvõrdeline kauguse ruuduga. Järelikult on ka väljatugevuse muut vektorina suunatud vaatleja X poole, seega paremale alla. Tugevnev elektriväli tekitab tugevneva magnetvälja, mille jõujooned ümbritsevad parempoolsete pööristena elektrivälja tugevuse muudu vektorit . Nad ümbritsevad punktis 1 vektorit samamoodi, nagu nad joonise vasakpoolses ülemises osas ümbritsevad vooluga juhet, olles suunatud juhtme taga üles ja ees vasakul alla.
Seega tekib punktist 1 vasakul alla suunatud ja tugevnev magnetväli magnetinduktsiooniga . Kuna see väli on tugevnev, siis on alla suunatud ka magnetinduktsiooni muut . Vektoritega ja samal sihil allpool paiknev vaatleja Y registreerib tugevnevat magnetvälja samamoodi nagu siis, kui tema poole liiguks ülalt alla püsimagnet, põhjapoolus ees. Kui see magnet läbiks liikudes juhtmerõngast, siis tekiks selle rõnga parempoolses tagumises ääres tahapoole (vasakule üles) ning rõnga vasakpoolses esiääres ettepoole (paremale alla) suunatud induktsioonivool, mida võib vaadelda põhjustatuna samamoodi suunatud pööriselektriväljast tugevusega . Pööriselektrivälja jõujooned ümbritsevad vasakpoolsete pööristena magnetvälja kasvu suunda. Nende pööriste vasakpoolsus tuleneb elektromagnetilise induktsiooni seaduses (valem 2.7 ) sisalduvast miinusmärgist.
Samamoodi tekib paremale alla suunatud pööriselektriväli tugevusega , ka punktis 2, mis ju samuti jääb horisontaaltasandis paikneva ning suunda ümbritseva pöörise vasakule esiäärele. Võime teha kokkuvõtte: muutuv elektriväli tugevusega on magnetvälja vahendusel ruumis vasakule ettepoole liikunud. Temast on saanud väli . Punktis 2 aga kordub seesama protsess, mis leidis aset punktis 1. Horisontaaltasandis paiknev, paremale ette suunatud elektriväli tekitab endast vasakul eespool vertikaaltasandis paikneva ja alla suunatud magnetvälja . Võime nentida: magnetväljast on elektrivälja vahendusel saanud magnetväli . Ehk teisisõnu, magnetväli on elektrivälja vahendusel liikunud vasakule ettepoole. Seega elektromagnetväli liigub ruumis lainena algse elektrivälja muutusega ristuvas suunas. Elektriväli ja magnetväli on laines omavahel risti ja nad mõlemad on ka risti laine levimissuunaga. Elektromagnetlaine on ristlaine.
Olgu öeldud, et täpselt samamoodi kiirgaks elektromagnetlaineid raadio saateantenn, mille juhtme tükk paikneb joonise 3.1vasakpoolses ülemises osas ja mille juhtmes kulgeks ajas muutuv vool. Elektromagnetlained kiirguvad juhtmega ristuvas suunas, joonisel 3.1 vasakule alla.
| Heinrich Rudolf Hertz (1857 - 1894). 1887. aastal tegi ta rea eksperimente, kus suutis esmakordselt tekitada ja ka detekteerida elektromagnetlaineid, samuti demonstreerida nende polarisatsiooni ja interferentsi. Maxwelli võrrandite formuleerimisest oli selleks ajaks möödas juba kakskümmend aastat. | Hertz suutis oma katseseadmes tekitada piisavalt suure sagedusega elektrivõnkumisi (sagedusega ca 500MHz). Tagumisel laual on näha kõrgepinget tekitanud pool. Antenniks oli esiplaanil kahe suure sfääri vahel paiknev varraste süsteem. |
Kogu meid ümbritsev ruum on täidetud elektromagnetlainetega. Õnneks me lõviosa nendest ei taju, muidu oleks võimatu aru saada, mis meie ümber toimub.
Elektromagnetlainetel võivad olla väga erinevad omadused ja seepärast on neil ka erinevad nimed. Suurt osa elektromagnetlaineid kutsutakse kiirgusteks.
Ühe osa neist lainetest on inimene tekitanud ja pannud need ennast teenima. Näiteks raadiolained kannavad edasi infot, lambivalgus lubab inimestel pimeda ajal näha, infrapunakiirgus ehk infravalgus aitab teleri puldi abil mängima panna. Aga ka tavaline vahelduvvool juhtmes tekitab elektromagnetlaineid.
Teine osa lainetest aga tekib niisama, ilma inimese osaluseta. Näiteks Päikeselt tulev ultraviolettkiirgus ehk ultravalgus päevitab meid kenasti pruuniks, radioaktiivne kiirgus, mis tekib radioaktiivsete ainete lagunemisel, ohustab meie tervist, jaaniusside salapärane kuma rõõmustab meid suveööl.
Elektromagnetlainete toime sõltub lainete sagedusest ehk ajaühikus toimuvate võngete arvust. Samas sõltub see ka lainepikkusest ehk naaber-laineharjade vahekaugusest. Nende kahe suuruse seos tuleneb ühtlase liikumise kiiruse valemist . Teepikkuseks s on laine korral lainepikkus , mille läbimiseks kuluv aeg on võnkeperiood . Perioodi pöördväärtus on aga sagedus . Seega
laine levimiskiirus on lainepikkuse ja sageduse korrutis. Kui tegemist on elektromagnetlainetega vaakumis, siis asendub valguse kiirusega vaakumis ning lainepikkuse all tuleb mõista lainepikkust vaakumis, niisiis
Sageduse mõõtühikuks on . Elektromagnetlainete korral peetakse silmas E- või B-vektori võnkumisi. Lainepikkuse mõõtühikuks on .
Valem 3.1 põhjal on lainepikkus vaakumis ja sagedus omavahel pöördvõrdelised:
Näide 3.1.
Tühjuses (vaakumis) levib elektromagnetlaine suurima võimaliku kiirusega maailmas, mis on kõigi vaatlejate jaoks ühesugune. Füüsikalise looduskäsitluse aluste kursuses nimetati seda kiirust absoluutkiiruseks ja tähistati tähega (kr celeritas – kiirus). Teatavasti absoluutkiirus c = 299 792 458 m/s ≈ 3·108 m/s.
Elektromagnetlaine üleminekul ühest keskkonnast teise võib laine kiirus muutuda. See kutsub esile ka lainepikkuse muutumise, kuid laine sagedus sealjuures ei muutu kunagi.
Ülevaate saamiseks kõikvõimalikest elektromagnetlainetest on kombeks paigutada nad sageduse või lainepikkuse järgi astmikule ehk skaalale, mille ühes otsas paiknevad madalsageduslikud ja pikad, teises (parempoolses) otsas aga kõrgsageduslikud ja lühikesed lained. Saame nn elektromagnetlainete skaala. Järgnevalt loetletud elektromagnetlainete põhiliigid erinevad lisaks sagedusele või lainepikkusele veel tekkimise viisi, levimise seaduspärasuste ning ainest läbitungimise võime poolest.
Madalsageduslained (, ja enam) on sisuliselt vahelduvvool, millega lähem tutvumine seisab meil ees Energia kursuses. Need lained levivad elektrijuhtides. Vaakumis või dielektrikus (näiteks õhus) on vastava elektromagnetvälja energia ja seega ka lainete intensiivsus tühiselt väikesed. Nimetatud põhjusel kantaksegi vahelduvvooluga kaasneva elektromagnetvälja energiat (ehk kõnekeeles lihtsalt elektrienergiat) üle juhtmete abil.
Raadiolained (, ) kaasnevad vahelduvvooluga, mida me uurime lähemalt Energia kursuses. Võnkumisi tekitab elektrooniline generaator ja vastavaid laineid kiirgab raadioantenn. Ajaloolise tava kohaselt jagatakse raadiolainete piirkonda omakorda millimeeter- ja sentimeeterlainealaks lainepikkustega vastavalt 1...10 mm ja 1...10 cm (satelliittelevisiooni ning radarite tööpiirkond), televisiooni detsimeeter- ja meeterlainealaks (lainepikkustega 1...10 dm ja 1...10 m), raadio ultralühilainealaks (levinuim lainepikkus 3 m) ning raadio lühilaine (λ = 10...100 m), kesklaine (λ = 100...1000 m) ja pikklaine alaks (lainepikkus üle 1000 m).
Optiline kiirgus (, ) on peaosatäitjaks valgusnähtustel. Pikalaineline optiline kiirgus tekib molekulide võnkumistel, aga peamiselt tekitavad optilist kiirgust siiski aatomite väliskihtide elektronid. Optiline kiirgus jaguneb omakorda ultravalguseks (λ = 10…380 nm, 1 nm = 10-9 m), nähtavaks valguseks (λ = 380...760 nm) ja infravalguseks (λ = 760 nm...1 mm).
Röntgenikiirgus (, )
tekib kas kiirete elektronide järsul pidurdumisel või siis protsessidel, milles osalevad aatomite sisekihtide elektronid. Röntgenikiirguse lainepikkuse suurusjärk ühtib aatomite vahekaugusega tahkistes. Meditsiinis leiab laialdast kasutamist röntgenikiirguse võime tungida läbi inimkeha.
Gammakiirgust (, ) väljastavad radioaktiivsel lagunemisel aatomite tuumad. Gammakiirguse laineomadusi on raske uurida, sest lainepikkus on väiksem aatomi mõõtmetest. Gammalainet pole enam millegagi võrrelda. Gammakiirgus tungib raskusteta läbi peaaegu igast ainest.
Nagu näeme, kaasneb kiirgaja mõõtmete vähenemisega ülaltoodud reas (antenn → molekul → aatomi väliskiht → aatomi sisekiht → tuum) lainepikkuse vähenemine ja sageduse suurenemine. Koos sagedusega suureneb ka kiirguse energia ning läbitungimisvõime.
Peab lisama, et erinevate lainepiirkondade vahel puuduvad täpsed piirid. Jaotuse aluseks on eelkõige laineallikad, kusjuures erinevate laineallikate poolt tekitatud lainete sagedused kattuvad. Kõikidest elektromagnetlainetest näeb inimese silm ainult seda osa, kus laine sagedus jääb vahemikku 1014...1015 Hz. Sellise sagedusega elektromagnetlaineid nimetatakse nähtavaks valguseks. Teistel elusolendeil võivad tekitada nägemisaistingu aga teistsuguste sagedustega elektromagnetlained. Näiteks maod tajuvad hästi infravalgust, aga mesilased ultravalgust.
Elektromagnetlaineid tajub inimene lisaks nägemisele ka soojusena. Pole ju vaja käega katsuda, kas ahi või radiaator on soe, juba eemalt tunneme, kuidas see "sooja õhkab". Seda tunnet tekitavad elektromagnetlained, mille sagedus jääb vahemikku 1012...1014 Hz.
Elektromagnetlaineid kasutab inimene väga paljudes eluvaldkondades. Paljudega neist saame me põgusalt tuttavaks järgnevates alajaotustes.
Tänapäeval osatakse käsitseda pea kõikvõimalike lainepikkuste ja sagedustega elektromagnetlained. Peatüki lõpetuseks esitame joonisel 7-10 elektromagnetlainete spektri skeemi, ühtlasi täpsustades mõningaid nendega seotud mõisteid.
Nähtava valguse pikalainelisest punasest servast edasi tuleb nähtamatu infrapunavalgus ehk lihtsalt infravalgus. Seda tajume tema soojusliku toime kaudu. Infravalgus läheb järkjärgult üle raadiolaineteks, millest lühimad on ultralühilained ehk mikrolained Teravat piiri nende piirkondade vahel ei ole. Tanapaeval kasutatakse raadiosides ja teabelevis kõiki lainepikkusi alates umbes ühest mikromeetrist lähi-infravalguses kuni ühpdckade raadiolaineteni, mille pikkus küünib tuhandete kilomeetntem. on viirutatud. Esimesi rakendatakse kiudoptilistes sidesüsteemides, viimaseid sidepidamiseks sukeldunud allveelaevadega. Lühilainelisel poolel läheb ultraviolett- e. ultravalgus üle röntgenikiirteks, mille lainepikkused on lähedased aatomi mõõtmetega, edasi gammakiirteks, millest lühimate lainepikkused ei ulatu isegi aatomituuma mõõtmeteni.
Välja arvatud nähtav valgus, on kõik need kiirgused avastatud pärast Maxwelli eluaega. Tema loodud elektri, magnetismi ja valguse ühendteooria viis otseteed neist mõnede avastamisele, aidates mõista ka ülejäänuid. Vaevalt võib tuua paremat näidet puhta teaduse tulemustest, mis oleksid andnud nii tohutu tähtsusega praktilisi rakendusi. Kui nüüdsed teadlased püüavad õigustada maksumaksjate raha kulutamist asjadele, millel ei ole veel ilmset või kohest praktilist rakendust, on nad tänu võlgu James Clerk Maxwelli varjule.
Optika ehk valgusõpetus kirjeldab valguse tekkimist, levimist ja kadumist. Optikas nimetatakse valguse tekkimist kiirgumiseks ja valguse kadumist neeldumiseks. Kiirgumine seisneb selles, et aineline objekt tekitab oma energia arvel täiendava väljaportsjoni ehk kvandi. Neeldumisel annab kvant oma energia ja impulsi mingile ainelisele objektile ära ning haihtub ise olematusse. Ehk siis selleks, et valgus tekiks, peab olema keha, mis sel moel muudab teisi energialiike valguseks. Sellist keha nimetatakse valgusallikaks.
Näiteks nii hõõglambis kui valgusdioodlambis muudetakse valgusenergiaks elektrienergiat. Seejuures kiiratakse hõõglambis suurem osa (üle 80 %) muundunud elektrienergiast infravalgusena (soojuskiirgusena), aga valgusdioodlambis nähtava valgusena. Valgusdioodlampi tuntakse ka LED-lambina (ingl.k. light emitting diode).
Valguse levimine toimub erinevalt vaakumis või mingis keskkonnas ehk aines.
Vaakumis levib valgus nagu iga elektromagnetlaine: muutuv elektriväli tekitab muutuva magnetvälja ja see omakorda uuesti muutuva elektrivälja ning kõik kordub. Nii kandub valgus ruumis edasi kiirusega c.
Valgus levib ühtlases ehk homogeenses keskkonnas sirgjooneliselt. Mitteühtlases keskkonnas levib valgus kõverat teed pidi.
Valguse levimise teed saab leida looduses kehtiva printsiibi järgi, mis väidab, et valgus levib teed mööda, mille läbimiseks kulunud aeg on minimaalne. Seda printsiipi tuntakse Fermat' printsiibina, sest selle sõnastas 1662. aastal prantsuse matemaatik Pierre de Fermat. Kui keskkond on ühtlane, siis kõige kiiremaks levimisteeks on sirge, aga kui keskkond ei ole ühtlane, siis pole kiireim tee sugugi sirge. Seda väidet saab illustreerida järgmise näitega.
Oletame, et me oleme järve kaldal ja äkki hakkab järves keegi uppuma (J.3.2). Uppujale tuleks appi jõuda nii kiiresti kui võimalik. Kas joosta punkti 1 ja ujuda otsejoones uppujani või on mõni teine variant otstarbekam?
Tuleb arvestada, et inimene jookseb kiiremini kui ujub ja sellepärast tuleks ujumismaad lühendada ja jooksmismaad pikendada. Sellepärast tulekski joosta punkti 2 ja sealt uppujani ujuda. Punkti 2 täpse asukoha saab välja arvutada, aga uppuja päästmisel pole selleks aega ning valik tuleb teha oma sisetunde järgi.
Kui valgus langeb mingile kehale, siis võib valgus kas kehalt peegelduda, kehast läbi minna või kehas neelduda. Ükski nendest protsessidest ei toimu täielikult. Ka kõige parem peegel ei peegelda valgusest 100 %, mingi osa valgusest siiski neeldub peeglis. Samuti ei lase ka kõige puhtam aknaklaas läbi kogu valgust, ikka neeldub mingi osa valgusest klaasis.
Kui valgus langeb ainele, mis valgust läbi ei lase ja ei peegelda ka, siis öeldakse, et valgus neeldus selles aines. Lihtsamalt öeldes: valgus kadus ära. Aga me teame, et kehtib energia jäävuse seadus, järelikult pidi neeldumisel valgusenergia muutuma mõneks teiseks energialiigiks. Tavaliselt muutub neeldunud valgusenergia soojuseks, kuid see võib muutuda ka näiteks elektrienergiaks, nagu see juhtub päikesepatareides.
Valgus ei neeldu aines kunagi täielikult, sest ka kõige mustem pind peegeldab natuke valgust tagasi. See hulk võib olla küll tühine, aga nulliks ei saa see kunagi. Näiteks tahma korral peegeldub sellele langenud valgusest tagasi vähem kui 0,1 %.
Elektromagnetväli
Elektromagnetvälja levimine
Elektromagnetväli levib ruumis elektromagnetlainena, milles elektriväli ja magnetväli perioodiliselt muutuvad.
Väljavektorite suund elektromagnetlaines
Elektromagnetlainete põhiliigid
Elektromagnetlainete põhiliikideks on madalsageduslained, raadiolained, optiline kiirgus (infravalgus, nähtav valgus ja ultravalgus), röntgenikiirgus ja gammakiirgus.
Elektromagnetlainete tekkimine
Elektromagnetlaineid võib tekitada nii inimtegevus kui looduslikud protsessid.
Elektromagnetlainete skaala
Elektromagnetlainete skaala on diagramm, kus kõik elektromagnetlainete liigid on reastatud sageduse või lainepikkuse järgi.
Elektromagnetlainet kirjeldakse samade suurustega, mis on meile tuttavad Mehaanika kursuses mehaaniliste lainete õppimisest: amplituud, hälve, lainepikkus, periood, sagedus, ringsagedus, faas ja levimiskiirus. Käesolevas kursuses kirjeldame me nende suuruste abil E-vektori ja B-vektori ajalist käitumist. Elektrivektori kohta kirjutame harmoonilise võnkumise võrrandi kujul
kus on E-vektori hetkväärtus ehk hälve, selle vektori amplituudväärtus, on aeg, on ringsagedus ja siinusfunktsiooni argument on laine faas. B-vektori kohta kirjutame vastavalt , kus on B-vektor ja selle amplituudväärtus. Selliseid laineid saab esitada kahesuguste graafikutega. Ühel juhul näidatakse, kuidas ühes kindlas ruumipunktis muutub aja jooksul E-vektori väärtus. Teisel juhul näidatakse, millised on E-vektori väärtused ühel ajahetkel mingis ruumipunktis.
Valgus on üks elektromagnetlainete liik. Kuid käesolevas kursuses ei kasuta me valguslaine kirjeldamisel magnetvälja, räägime ainult E-vektorist. Sellisel lihtsustusel on vähemalt kaks põhjust. Esiteks on elektromagnetlaine moodustavad E-vektor ja B-vektor risti ning nad võnguvad samas faasis (vaata J.3.3). Järelikult ei ole meil tarvidust neid mõlemaid välja joonistada, kui me teame üht siis teame automaatselt ka teist. Ja kuna vaid kahemõõtmelist lainet on võimalik korralikult paberil või arvutiekraanil kujutada, siis jäetaksegi B-vektor tihti vaatluse alt välja. Teine põhjus seisneb selles, et valgusaistingu silmas või signaali mõnes tajuris tekitab just valguslaine elektriväli, mõjudes neis olevatele elektronidele.
Valguslained eristuvad teistest elektromagnetlainete liikidest selle poolest, et nad tekitavad inimesel valgusaistingu. Selliste lainete sagedus jääb vahemikku 3,95·1014... 7,9·1014 Hz ja lainepikkus vahemikku 760...380 nm.
Kõiki füüsikalisi suurusi peab olema võimalik mõõta. Aga E-vektori muutumissagedus on ca 1014 Hz ja nii kiiresti muutuvat suurust pole võimalik ühegi riistaga mõõta. Sellepärast kasutatakse E-vektori keskmist väärtust. Täpsemalt öeldes, kasutatakse E-vektori ruudu keskväärtust E2kesk. See on ühe laine korral muutumatu suurus ja seda on võimalik mõõta.
Suurust, mis on võrdeline E2kesk-ga, nimetatakse valguslaine tugevuseks ehk valguse intensiivsuseks:
kus on võrdetegur. Intensiivsus näitab valgusenergia hulka, mis ajaühikus langeb pinnaühikule. Selle mõõtühikuks on
Mida suurem on E-vektori amplituud, seda suurem on ka E2kesk ja seega ka suurem valguse intensiivsus. Selline seos kehtib kõigi elektromagnetlainete korral.
Olukord on sarnane teiste lainetega. Näiteks madalad, väikese amplituudiga veelained ei lõhu merekallast, küll aga kõrged lained, millel on rohkem energiat.
Valguslaine ei ole mingisuguse keskkonna võnkumine nagu veelaine on vee võnkumine. Valguse korral muutub ainult E-vektori väärtus. Järelikult pole valguslaines ka mingeid laineharjasid ega -nõgusid. On ainult E-vektori maksimaalsed ja minimaalsed väärtused.
Valguse intensiivsuse asemel kasutatakse valgustehnikas mõistet kiiritustihedus, mida mõõdetakse ka ühikutes W/m2. Et saada ettekujutus sellise ühiku suurusest, võib aluseks võtta fakti, et südasuve keskpäeval, selge ilmaga on Eestis päikesevalguse intensiivsus ehk kiiritustihedus maapinnal veidi vähem kui 700 W/m2.
Valguse kiirus on erinevates keskkondades erinev. Kehtib seaduspärasus, et mida suurem on keskkonna tihedus, seda väiksem on seal valguse kiirus. Näiteks õhus normaaltingimustel on valguse kiirus v = 2,9970·108 m/s, mis on praktiliselt võrdne valguse kiirusega vaakumis. Seevastu ühes suurema tihedusega läbipaistvas aines, teemandis, on valguse kiirus punase valguse jaoks ca 1,24·108 m/s.
Valguslainete ja mistahes elektromagnetlainete levimist kirjeldatakse samamoodi nagu lainete levimist mehaanikas. Laine levimist ruumis kirjeldab lainefront (J.3.5). Lainefront on pind ruumis, kus kõik laine punktid võnguvad ühes faasis. Näiteks, kui veelaineid ülevalt vaadata, siis lainefrontideks võivad olla kõik laineharjad.
Joonistel esitatakse lainepinnad iga perioodi järel, lainepindade vahekaugus on võrdne ühe lainepikkusega.
Lainefrontide kuju järgi nimetatakse ka lainete tüüpe. Elektromagnetlainete uurimisel on kõige olulisemad neist keralained ja tasalained. Esimesel juhul on lainefrondiks kerapind ehk sfäär, mida joonisel kujutatakse ringjoonena. Lainefrondid moodustavad sel juhul kontsentriliste sfääride (joonisel ringide) süsteemi. Teisel juhul on lainefrondiks tasand, mida joonisel kujutatakse sirge joonena. Lainefrondid moodustavad sel juhul paralleelsete tasapindade (joonisel sirgete) süsteemi (J.3.5).
Lainefrontide ristsirgeid nimetatakse kiirteks.
Punkvalgusallikast hakkab ühtlases keskkonnas levima keralaine. Kui laine on allikast juba väga kaugele jõudnud, siis muutuvad lainefrondid väiksemas ruumipiirkonnas paralleelseteks ja seal võib rääkida tasalainest (J.3.6).
Kui on teada üks lainepind, siis järgmise saab leida, kasutades Huygensi printsiipi: lainefrondi iga punkt on uue laine allikaks. Neid uusi laineid nimetatakse elementaar- või sekundaarlaineteks, mis on keralained. Järgmise lainefrondi leidmiseks tuleb leida sekundaarlainete puute- ehk mähispind (J.3.7).
Tõkestamata laine levib ainult frondi esialgse levimise suunas. Teistes suundades lained kustutavad üksteist, st alati leidub mingi sekundaarne allikas, kus võnkumised on vastandfaasis sinna jõudva lainega ja lained kustuvad.
Valgeks valguseks nimetatakse Päikeselt tulevat valgust ehk päikesevalgust, mis sisaldab kõikvõimalikke värvilisi valgusi. Sageli öeldakse päikesevalguse asemel päevavalgus, mille all mõistame valgust, mis tuleb päevasel ajal nii selgest taevast kui läbi pilvede. Tinglikult võib valgeks pidada ka hõõglambi valgust, kuigi selles on punast ja kollast valgust rohkem kui päevavalguses. Paremini sarnaneb päevavalgusele säästulambi valgus.
Valguse lainepikkus on meie jaoks imeväike. Kui kasutada piltlikku võrdlust, siis on valguse lainepikkus žiletitera paksusest keskeltläbi samapalju väiksem kui inimese pikkus on väiksem teletorni kõrgusest.
Sellele vaatamata on erineva lainepikkusega valguslaineid üksteisest eristada küllalt lihtne. Seda saab teha ka silma järgi, kuna erineva lainepikkusega valguslained põhjustavad erinevaid värvusaistinguid. Näiteks, kui meie silma satub valgus, mille lainepikkus , tekib meil mingi värvusaisting. On kokku lepitud, et seda värvust nimetatakse roheliseks. Kui aga lainepikkus on 650 nm, siis tekib punase värvuse aisting. Inimsilm on nii tundlik, et see võib tajuda erinevaid värvitoone, kui lainepikkus erineb ainult 5 nm võrra.
|
Värvus |
Lainepikkus, nm |
|
Punane |
760…630 |
|
Oranž |
630…600 |
|
Kollane |
600…570 |
|
Roheline |
570…520 |
|
Helesinine |
520…470 |
|
Sinine |
470…420 |
|
Violetne |
420…380 |
Kõiki värvusi on võimalik saada, kui liita erinevas vahekorras kahte või kolme põhivärvust. Põhivärvused on punane (R), roheline (G) ja sinine (B). Neid värvusi kasutatakse ka televiisori või arvuti ekraanil pildi tekitamiseks.
Värvuste liitmiseks tuleb erinevat värvi valgused näiteks juhtida valgel ekraanil ühte kohta. Televiisori või arvuti kuvaril on erivärvilised täpikesed ekraanil üksteisele aga nii lähedal, et meie silm ei suuda neid eristada ja nad liituvad meie silmas iseenesest.
Värvuste liitmist ei tohi segi ajada värvide liitmise ehk segamisega. Kui segada punast, rohelist ja sinist värvi, saame tulemuseks mingi tumeda värvi, pruunikasmusta.
Värviliste valguste korral kasutatakse nn RGB süsteemi (red, green, blue), kus aluseks on värvused, mis vastavad kindlatele lainepikkustele: R = 700,0 nm; G = 546,1 nm; B = 435,8 nm. Neist kaks viimast vastavad elavhõbeda kiirgusspektris esinevatele joontele.
Põhivärvuste liitmisel võib saada ka valget valgust. Retsept on järgmine: tuleb liita punast, rohelist ja sinist valgust nii, et nende intensiivsused suhtuksid kui
1 : 4,6 : 0,06.
Kuidas aga värvusi liita? Selleks tuleb valgele ekraanile juhtida üheaegselt erinevate lainepikkustega valgusvihud. Nende saamiseks võib kasutada värvilisi klaase, nn. valgusfiltreid, mis pannakse valge valguse allika (näiteks hõõglambi) ette. Punane klaas laseb läbi punast valgust, roheline rohelist ja sinine sinist. Ekraanil värvused liituvad.
Erinevaid värvitoone võib saada ka erinevate värvainete või värvide segamisel. Näiteks on meil midagi vaja värvida roheliseks, aga rohelist värvi ei ole, küll on aga sinist ja kollast värvi. Mida teha? Tuleb segada kokku sinist ja kollast värvi ning saamegi rohelise värvi. Selline värvide liitmine on nn CMYK süsteemi aluseks, mida kasutatakse värvitrüki korral. Tähed lühendis tähistavad: C – tsüaan (sinine); M – magenta (roosa); Y – kollane; K – must (K on viimane täht sõnast black). Kui RGB süsteemi põhivärvuste segamisel saame valge valguse, siis CMYK süsteemi põhivärvide segamisel saame musta värvi.
Enamik inimesi tajub värvusi ühtviisi, kuid leidub inimesi, kellel esineb kõrvalekaldumisi normaalsest värvusnägemisest. Neid inimesi nimetatakse värvipimedateks. Täieliku värvipimeduse puhul näib kogu maailm must-valgena, kus kõik on kas must, valge või hall. Niisugust värvipimedust esineb väga harva. Rohkem esineb osalist värvipimedust. Peamiselt ei suudeta eristada punast ja rohelist värvust. Selle häda all kannatajad näevad kõiki värvusi kahes värvitoonis: kollakas ja sinakas. Niisugust värvipimedust nimetatakse ka daltonismiks. See on tuletatud inglise keemiku ja füüsiku John Daltoni nimest, kes 1794. aastal avastas nähtuse iseenda juures.
Õppisime Füüsikalise looduskäsitluse aluste kursuses, et kogu meile teadaolev universum koosneb ainest ja väljast. Ainel ja väljal on väga erinevad omadused. Näiteks mingi osakene asub ruumis kindlas kohas ja tal on kindlad mõõtmed. Aga väljal, mida see osake tekitab, ei ole mõõtmeid, see levib lainetena üle kogu ruumi.
Oleme ka rääkinud, et atomistlik printsiip kehtib ka väljade kohta. Makromaailmas pidevana tunduv väli osutub mikrotasemel samuti koosnevaks jagamatutest osakestest, mida nimetatakse välja kvantideks.
Käesolevas peatükis me uurime elektromagnetlaineid ning sellega seoses tutvume veel ühe looduse fundamentaalse printsiibiga. Selgub nimelt, et ühelt poolt saab loodust kirjeldada ainena (osakestega), mida võib põhimõtteliselt "näha ja katsuda". Teisalt saab neidsamu nähtuseid kirjeldada ka väljadega, mida pole näha, kuid mis vahendavad osakeste vahel mõjuvaid jõude. Sellist omaduste kahesust nimetatakse dualismiks (lad duo – kaks). Looduses vastab igale lainele osake ja iga osakesega kaasneb laine. Näiteks elektrone, mida me oleme joonistel harjunud nägema ümber aatomi tuuma tiirlevate pallikestena, saab kirjeldada ka lainete abil (selliseid laineid nimetatakse ka De Broglie laineteks).
Ka valgust saab kirjeldada kaheti. Siiani oleme rääkinud valgusest kui elektromagnetväljast, mis levib ruumis lainena. Selgub aga, et valgust saab kirjeldada ka osakeste abil, nimelt on olemas valguse osakesed ehk kvandid. Valguse kvanti nimetatakse footoniks (kr phos – valgus).
Footonitest oleme juba rääkinud kursuses Füüsikalise looduskäsitluse alused. Sealt saime teada, et footon on osake, millel seisumass on võrdne nulliga, see tähendab, et paigalolekus footon olla ei saa. Teisiti öelduna: kui footon peatatakse, siis muutub ta millekski muuks, tema energia muutub mõneks teiseks energialiigiks.
Valguse kvantiseloom ilmneb selgemalt valguse kiirgumisel (tekkimisel) ja neeldumisel (kadumisel). Laineline olemus tuleb esile peamiselt valguse levimisel.
| Kahe pilu interferentsi eksperiment, mida saab läbi viia igasuguste lainetega, olgu selleks siis valgus või vee lainetus. | Kui valgus on nii nõrk, et tundlik detektor näeb iga footoni neeldumist, siis interferentsipilt tekib sellegipoolest - vaadake video lõpuni. See katse on üks ilusamaid valguse dualistlikku iseloomu demonstreeriv katse. |
Valguse lainelised ja korpuskulaarsed (osakesetaolised) omadused ühendas omavahel M. Planck 1900. aastal, kui ta võttis kasutusele valemi
kus on footoni energia, vastava valguslaine sagedus ja võrdetegur, mida tuntakse Plancki konstandina: TeX parse error: '\cdot' is only supported in math mode. Toodud valem kehtib kõigi elektromagnetlainete korral, mitte ainult valguse puhul.
Ühe footoni energia on nii väike, et seda otseselt mõõta on võimatu. Näiteks sääse ühe tiivalöögi energia on keskmiselt 1012 (miljon miljonit) korda suurem footoni energiast.
Footonite olemasolu tõestati fotoefekti katsetega. Fotoefektiks, täpsemalt välisfotoefektiks nimetatakse elektronide väljalöömist ainest (J.3.8, a). On olemas ka sisefotoefekt, mille korral valgus lööb elektrone välja keemilistest sidemetest aatomite vahel, aga elektronid ainest ei välju. Sisefotoefekt on näiteks päikesepatareide töö aluseks.
Välisfotoefekti uurimiseks kasutame katseseadet, mille skeem on toodud joonisel. 3.8 b.
Katsete tulemused võib kokku võtta järgnevalt:
- Kui elektroskoobiga ühendatud metallplaat laadida negatiivselt, siis selle valgustamisel kaob laeng mõne aja jooksul
- Kui plaat laadida positiivselt, siis laeng valguse toimel ei kao
- Kui me plaati üldse ei lae, siis valguse toimel plaat ei laadu
- Kui asetada valguse teele klaasplaat, siis ei kao ka negatiivselt laetud plaadi laeng
Teeme katsetest järeldused.
Esimene katse näitas, et valguse toimel kadus plaadilt elektrilaeng. Kuna negatiivse laengu kandjad on elektronid, siis võib järeldada, et valgus lõi plaadist välja elektrone.
Viimane katse aga näitas, et kui valguse teel oli klaasplaat, siis ei löödud plaadist elektrone välja. Põhjus on selles, et klaas laseb läbi ainult nähtavat valgust, aga mitte ultravalgust. Järelikult mitte igasugune valgus ei vabasta elektrone, vaid ainult suurema kvandienergiaga valgus ehk ultravalgus. On ju ultravalguse sagedus suurem kui nähtaval valgusel ja seega on ultravalgusel ka suurem kvandienergia. Tuleb märkida, et välisfotoefekt võib esineda üksikute ainete korral ka nähtava valguse toimel.
Kui plaat polnud laetud, siis valguse toimel ei laadunud sellepärast, et väljalöödud elektronid tõmmati plaati tagasi. Põhjus on selles, et enne oli plaadis elektronide negatiivsete laengute ja prootonite positiivsete laengute summa null. Aga elektronide lahkudes jäi ülekaalu prootonite positiivsete laengute summa ja plaat omandas positiivse laengu.
Kui plaat juba on positiivselt laetud, siis tõmmatakse väljalöödud elektrone plaati tagasi veel tugevamini kui laadimata plaadi korral.
Välisfotoefekti avastas 1887. aastal H. Hertz, kui ta uuris elektroodide vahel tekkivat sädelahendust. Ta märkas, et säde tema elektromagnetlainete tekitamiseks loodud katseseadmes tekkis paremini, kui elektroode valgustada. Põhjalikumalt uuris efekti A. Stoletov 1888. aastal. Kuid nemad ei osanud nähtust seletada. Seda tegi A. Einstein footonite abil 1905. aastal ja talle anti selle eest 1921. aastal Nobeli füüsikapreemia. Einsteini teooria sisu võtab kokku valem, mida tuntakse kui Einsteini valemit fotoefekti kohta.
kus on Plancki konstant, – valguse sagedus, – väljumistöö (töö, mida peab valguskvant tegema, et vabastada elektron positiivsete ioonide tõmbejõududest), – elektroni mass ja – vabanenud elektroni kiirus.
Nägime, et valgusnähtusi seletatakse nii lainete kui kvantide abil. Sageli öeldaksegi, et valgus on olemuselt dualistlik ehk kahene. Täpsem oleks öelda, et mitte valguse olemus ei ole dualistlik, vaid dualistlik on meie käsitlus valgusest: mõnede nähtuse juures avaldub valguse laineline olemus, teiste korral kvantolemus.
Valguse laine- ja kvantteooriad ei ole vastandlikud, nad täiendavad teineteist. Mida see tähendab? Aga seda, et kui me käsitleksime valgust kui ainult elektromagnetilist lainet, siis jääks meile mõistetamatuks mitmed valgusega seotud nähtused nagu juba eespool mainitud fotoefekt või valguse rõhk. Siis oleks leiutamata ka laserid ja kõik nendega seotu alates laserite kasutamisest meditsiinis ja lõpetades CD- ja DVD-mängijatega. Ja kui me käsitleksime valgust kui ainult footonite voogu, siis oleks meil keerulisem seletada valguse difraktsiooni ja interferentsiga seotud nähtuseid.
Mida väiksem on elektromagnetlaine sagedus , seda väiksem on ka kvandi energia , sest . Ja ühe kvandi energia võib olla nii väike, et meil ei ole võimalik seda avastada. Näiteks raadiolainetel, sagedusega 100 MHz, on ühe kvandi energia nii väike, et raadios registreeritava signaali tekitamiseks peab antennini jõudma vähemalt 1010 kvanti sekundis. Sellise osakeste arvu puhul on võimatu neid üksteisest eristada ja neid võib käsitleda lainena.
Ka veelaine koosneb ülipaljudest veemolekulidest, aga keegi ei räägi veeosakeste liikumisest, vaid ikka veelainest.
Kimp suunatakse alumiiniumi mikrokristallide õhukesele kihile. Röntgenkiirte lainepikkus on λ. elektronid kiirendatakse energiani, kus nende de Broglie’ lainepikkus on samuti λ. Fotofilmil tekib nii röntgenkiirtest
Kuid suure sagedusega elektromagnetlainete, näiteks γ-kiirguse korral on nende lainelisi omadusi raske märgata. Sel juhul käitub kiirgus pigem osakese kui lainena. Näiteks juba ühest γ-kvandist piisab, et esile kutsuda tuumareaktsiooni nagu seda võib teha ka mingi osakene, näiteks neutron.
Valgusel, mis on sageduste poolest raadiolainete ja γ-kiirguse vahepealne, avalduvad nii lainete kui osakeste omadused. See on aga ebatavaline ja harjumatu, sest me ei oska endale midagi taolist ette kujutada. Midagi muud sarnast pole me looduses märganud. Oleme harjunud, et osakene asub ikka mingis kindlas kohas, aga laine täidab mingi osa ruumist. Valguse korral on aga osake ka samal ajal laine ja laine osake. Sellise ebatavalise olukorra põhjuseks on fakt, et inimene ei saa vahetult tajuda valguse olemust.
Valguslaine E-vektori kaudu
Valguslainet kirjeldatakse E-vektori kaudu, B-vektor jäetakse tavaliselt vaatluse alt välja.
Kera- ja tasalained
Valguslaineid kirjeldatakse kera- või tasalainete abil. Esimestel on lainefrondiks kera pind, teisel juhul tasand.
Põhivärvused
On olemas kolm põhivärvust: punane, roheline ja sinine (RGB), millest koosnevad kõik teised värvused.
Elektromagnetlainete difraktsioon ja interferents on põhimõtteliselt sarnased mehaaniliste lainete difraktsiooni ja interferentsiga. Mehaaniliste lainete difraktsiooni ja interferentsi käsitlesime Mehaanika kursuses. Tuletame kõigepealt lühidalt seal õpitu meelde.
Difraktsiooniks nimetatakse lainete kandumist teele jäävate tõkete taha. Näiteks veelained jõuavad vees oleva kivi taha ja kanduvad avade läbimisel varju piirkonda (vt J.3.9).
Interferentsiks nimetatakse lainete liitumist, mille tulemusena mõnes kohas lained muutuvad suuremaks (amplituud saab suuremaks kui ühe liituva laine amplituud), teises kohas väiksemaks (amplituud väheneb). Näiteks kui visata tiiki samaaegselt kaks kivi, siis kohtudes muutuvad tekkivad lained mõnes kohas suuremaks, teises kohas väiksemaks (vt J.3.10).
Veelainete abil saame endale ette kujutada ka elektromagnetiliste tasalainete ja keralainete difraktsiooni ja interferentsi – joonisel 3.9 kujutatud situatsioon on ühtlasi ristlõige tasalainete difraktsioonist pilult (pilu on suunatud risti joonisega) ning (joonisel 3.10) on ristlõige kahe keralaine interferentsist. Seda analoogiat saab kasutada elektromagnetlainete difraktsiooni ja interferentsi uurimiseks lainevannis.
Katses nähtud veelainete amplituudi suurenemist või vähenemist mõnes kohas aitab mõista (joonis 3.11). Seal on kujutatud kaks liituvat lainet mingis veepinna punktis. Liitlaine saamiseks tuleb liita lainete hälbed igal ajahetkel. Joonisel on toodud kolm juhtu. Joonise osas a on lained täpselt samas faasis, st lainete miinimumid ja maksimumid esinevad täpselt ühel hetkel mõlemas laines. Sellises olukorras tugevdavad lained teineteist maksimaalselt, liitlaine amplituud on võrdne liituvate lainete amplituudide summaga. Joonise osas b on lained täpselt vastandfaasis, st ühe laine maksimum esineb täpselt samal ajal, kui teisel lainel on miinimum. Sellises olukorras nõrgendavad lained teineteist maksimaalselt, liitlaine amplituud on võrdne liituvate lainete amplituudide vahega.
Loomulikult esineb rohkem selliseid kohti veepinnal, kus lained pole täpselt samas või vastandfaasis. Neis on liitlaine amplituud maksimaalse ja minimaalse vahepealne nagu on see joonise osas c.
Selleks et tekiks interferents, peavad liituvad lained olema koherentsed – see tähendab, et lainetel peab olema ühesugune lainepikkus ja nende faaside vahe ei tohi aja jooksul muutuda.
Kui me ütleme, et difraktsioon ja interferents esinevad ka elektromagnetlainete korral, siis tekivad kohe küsimused, millele polegi nii lihtne vastata.
Kui esineb valguse difraktsioon, siis valgus levib ka tõkete taha. Kas siis peaks olema võimalik näha "nurga taha"?
Kui esineb valguse interferents, siis peaks kahe valgusallika korral kuskil valguslained üksteist tugevdama ja kuskil nõrgendama. Kas kahe lambi põlemisel tekivad tühja toa põrandal heledamad ja tumedamad piirkonnad?
Mõlemale küsimusele peaksime vastama eitavalt, sest midagi sellist tavaelus ei juhtu. Aga miks?
Sellepärast, et me pole arvestanud kaht asjaolu, mida tuleb lainete difraktsiooni ja interferentsi uurimisel arvestada.
Esiteks, lained difrageeruvad (kalduvad sirgjoonelisest levimissuunast kõrvale) märgatavalt ainult siis, kui nende teele jäävad tõkete või avade mõõtmed on võrreldavad nende lainepikkusega.
Valguse lainepikkus on väga väike ja tavaelus nii väikesi objekte pole või me ei märka neid. Küll aga saab valguse difraktsiooni vaadelda selleks korraldatud katsetes.
Lepime kokku, et edaspidi räägime ainult avadest, kuigi kogu jutt kehtib ka tõkete korral.
Ava väiksuse nõude põhjendamine pole lihtne ja sellele annab vastuse ülikooli optikakursus. Meie piirdume ainult eksperimentaalse fakti konstateerimisega.
Ühe pilu difraktsiooni katses näeme, et pilust läheb osa laserivalgust otse läbi ja see tekitab difraktsioonipildi keskele nn tsentraalse täpi, mis on kõige heledam (J.3.12). Sellest kahele poole jäävad valgustäppide read, kus tsentraalsest täpist kaugenedes täppide heledus järjest väheneb. Need täpid on laserikiire kujutised ekraanil ja see tähendab, et osa valgust ei lähe läbi pilu otse edasi, vaid kaldub erinevatesse suundadesse pärast pilu läbimist.
Kui vähendada pilu laiust, siis vahekaugused täppide vahel suurenevad. Kui pilu laiust suurendada, siis täpid tõmbuvad kokku tsentraalse täpi ümber. Pilu suure laiuse (paarist millimeetrist suurem) korral ei ole difraktsioon jälgitav.
Teiseks esineb interferents ainult siis, kui valguslained on koherentsed. Tavalised laelambid aga ei kiirga koherentseid laineid, st neil pole ühesugune lainepikkus ja muutumatu faaside vahe. Selles, et lampidel pole ühesuguse lainepikkusega valgus, saame veenduda palja silmaga. Kui valgusallikas kiirgab mingi kindla lainepikkusega valgust, siis on see valgus ühevärviline. Kui valgus on "valge", siis on tegemist liitvalgusega, mis koosneb mitmete värvuste segust.
Lainete faaside kindlakstegemine pole silma järgi võimalik, see nõuab juba täpsemat uurimist.
Koherentseid valguslaineid kiirgab laser. Sellepärast kasutataksegi interferentsi ja difraktsioonikatsetes peamiselt laserivalgust.
Valguse difraktsiooni saab seletada Huygensi printsiibi alusel. Joonisel 3.13. on näidatud tasalainete läbiminek kitsast pilust. Varju piirkonda ("nurga taha", mis on joonisel hall) satub valgus pilu servades olevaist sekundaarlaine allikaist M ja N. Tegelikkuses on neid sekundaarallikaid muidugi palju rohkem, kust valgus varju piirkonda satub, aga neid kõiki pole joonisel kujutatud.
Nii saab seletada valguse levimist "nurga taha", aga siis peaks valgus täitma varju piirkonna ühtlaselt. Meie aga nägime valgustäppide rida, kus täppide vahel olid tumedad kohad. Sinna ilmselt valgus ei sattunud.
Püüame olukorda seletada joonisel 3.14.
Lainefrondi punktidest A ja B lähtuvad sekundaarlained. Need kohtuvad omavahel ja juhul kui lained on samas faasis nagu on punktis C, siis nad tugevdavad teineteist ning tekib valgustäpp. Kui aga kohtuvad lained on vastandfaasides, siis nad kustutavad teineteise ja tekib tume koht. See, milline on liituvate lainete faaside vahe, oleneb teepikkuste erinevusest, mis laineil tuleb liitumispunkti jõudmiseks läbida, antud juhul AC – BC või AD – BD. Seda teepikkuste erinevust nimetatakse käiguvaheks. Järelikult tekivad valgustäpid seal, kus kohtuvad sekundaarlained on samas faasis ja tumedad kohad seal, kus need lained on vastandfaasides. Sarnane olukord tekib ka pilu teises servas, sellepärast ongi täppide rida mõlemal pool tsentraalset täppi.
Kokkuvõtvalt võib öelda, et valguse difraktsioon ja interferents on otsesed tõendid selle kohta, et valgus on laine. Selle tõestamine, et valgus on just elektromagnetiline laine, on juba palju keerulisem.
Interferentsi maksimumide ja miinimumide tekkimise tingimused on toodud allpool.
Valguse interferentsimaksimumid tekivad kohtades, kus käiguvahe jaoks on täidetud tingimus
(J.3.15). Kohtades, kus valgust ei ole, on interferentsimiinimumid. Seal on täidetud tingimus
(J.3.16). Tuleb välja, et difraktsioon saab nähtavaks tänu sellele, et pärast pilu läbimist valguslained liituvad ja tugevdavad või kustutavad üksteist. Mitmest avast tulevad valguslained saavad liituda ainult sellepärast, et pärast ava läbimist kanduvad lained varju piirkonda. Kõik see näitab, et ei saa rääkida difraktsioonist ilma interferentsita ja vastupidi. Nimetusi difraktsioon ja interferents kasutatakse suuresti ajaloolistel põhjustel, mis sai alguse ajast, kui neid nähtusi ei osatud omavahel siduda.
Kui uurida valguslainete liitumist lähemalt, siis selgub, et lainete kohtumispunktis liituvad lainete E-vektorid, olenemata sellest, kui palju laineid on. Sellist nähtust nimetatakse elektriväljade superpositsiooniks ja seda kirjeldab kursusest Füüsikalise looduskäsitluse alused tuntud superpositsiooniprintsiip: summaarne elektrivälja tugevus antud punktis on võrdne kõikide E-vektorite summaga selles punktis. Superpositsiooniprintsiibi kehtivus on eksperimentaalne fakt, mis iseloomustab looduse omapära, ja seda ei ole võimalik põhjendada.
Joonisel 3.17 on toodud näiteid E-vektorite liitumisest valguslainete kohtumisel.
Esimesel juhul on liituvad lained samas faasis ja tulemuseks on valguse intensiivsuse suurenemine: ehk . Kui , siis ja .
Teisel juhul on liituvad lained vastandfaasides ja tulemuseks on valguse intensiivsuse vähenemine: ehk . Kui , siis ja .
Kindlasti oleme nautinud ilusaid värvilisi seebimulle või uudistanud mitmevärvilisi õlilaike veeloigu pinnal. Ka kiilide ja teiste putukate tiivad sillerdavad päikesevalguses mitmevärviliselt. Kogu see värvidemäng looduses on tingitud valguse interferentsist.
Järgnevalt vaatleme mõningaid interferentsi ja difraktsiooni tehnilisi rakendusi, kus inimene kasutab neid nähtusi oma huvides.
Difraktsioonivõre
Üheks väga kasulikuks tööriistaks valguse ja valgust kiirgavate objektide uurimisel on difraktsioonivõre, mis kujutab endast paljude paralleelsete pilude süsteemi (J.3.18, a). Pilud on kitsad ja tihti on nende tihedus kuni mõni tuhat pilu millimeetri kohta. Kõige tähtsamaks difraktsioonivõre iseloomustavaks parameetriks on võrekonstant, mis näitab pilude omavahelist kaugust (J.3.18, b).
Kui monokromaatne valgus läbib võre, siis tekivad kitsad interferentsiribad, millede analüüs lubab määrata valguse lainepikkuse.
Kui difraktsioonivõrele langeb monokromaatne valgus, siis kujuneb välja joonisel 3.19 a olev intensiivsuse jaotus. Joonisel 3.19 b on pilt, mida võib näha vaateekraanil, kui võrele langeb laserivalgus. Maksimumid on kitsad (seepärast kutsutakse neid ka difraktsioonipildi joonteks) ja neid eraldavad suhteliselt laiad tumedad piirkonnad.
J.3.18 b Difraktsioonivõre tekitamas interferentsipilti punktis P. J.3.19 a) Suure pilude arvuga
difraktsioonivõre abil saadud
intensiivsuse jaotus koosneb kitsastest maksimumidest, mis on tähistatud nende järguga m, b) Ekraanil on näha vastavad heledad ribad, nn jooned, mis siin on samuti tähistatud järguga m.
Heledate joonte asukoha leidmiseks kasutame joonistelt 3.15 ja 3.16 tuttavat protseduuri ning arvutame igalt pilult punkti P jõudnud valguste käiguvahed. Selgub, et interferentsi maksimumid tekivad suundades, kus on täidetud tingimus:
(J.3.19). Valemis 3.1 on võrekonstant, on nurk, mille võrra valgus muudab oma levimissuunda, on difraktsioonimaksimumi järk ja valguse lainepikkus. Asendades valemis 3.1 erinevad k väärgused saame teada, millistes suundades on jälgitavad k-ndat järku difraktsioonimaksimumid. Nende suundade vahele jäävad alad, kus valguslained nõrgendavad üksteist.
Kirjutades selle valemi kujul
näeme, et antud võre puhul mingit joont (näiteks 3. järku joont, kus ) iseloomustav nurk a sõltub kasutatud valguse lainepikkusest. Seega, kui suuname tundmatu lainepikkusega valguse difraktsioonivõrele ja mõõdame nurki, siis on valemi 3.1 abil võimalik määrata valguse lainepikkus.
Seega erineva värvusega valgused kalduvad difraktsioonivõrest läbi minnes erinevatesse suundadesse ja neid on võimalik üksteisest eristada. Me saame teada, millistest komponentidest liitvalgus koosneb.
Teeme mõttelise katse, mis võimaldab kindlaks teha, millist värvi valgusi mingi liitvalgus sisaldab. Olgu meil näiteks valgusallikas, mis kiirgab ainult kahte värvi valgust: sinist ja kollast. Koondame valguse läätse abil ekraanile ja näeme seal valgusallika rohelist värvi kujutist (J.3.20, a). Kujutis on roheline sellepärast, et seal kohtuvad nii sinine kui kollane valguses. Sinise ja kollase värvuse liitumisel saame rohelise värvuse.
Asetame nüüd valguse teele difraktsioonivõre (joon. 3.20, b). Sümmeetriateljele jääb ikkagi allika roheline kujutis. Kuid sellest kahele poole tekib rida siniseid ja kollaseid valgusallika kujutisi. Need on tingitud sellest, et sinise valguse lainepikkus on väiksem kui kollasel valgusel. Sellepärast tekivad kollase valguse difraktsioonimaksimumid sümmeetriateljest kaugemale, sinine valgus kaldub vähem kõrvale kui kollane.
Ülalkirjeldatud metoodikat nimetatakse spektraalanalüüsiks ning selle rakendamise näidetega tutvume jaotises 4.3.3
Selgendav kate
Kõik me oleme kindlasti märganud, et prilliklaasid või fotoaparaadi objektiivid paistavad mõne nurga alt vaadates natuke kollakad, rohekad või sinakad.Ilmselt on need pinnad millegagi kaetud, sest puhast klaasi võid vaadata kuidas tahes, mingit värvivarjundit peegeldunud valgusel pole. Milleks on vaja aga prilliklaase ja objektiive millegagi katta? Aga selleks, et need laseks rohkem valgust läbi.Neid katteid nimetatakse selgendavateks kateteks, sest need vähendavad peegeldunud valguse hulka ja sellega suurendavad klaasi läbinud valguse hulka. See muudab tekkiva kujutise selgemaks. Siit ka katte nimi. Selgendavaid katteid kasutatakse ka päikesepatareide katteklaasides, et suurendada valguse hulka, mis jõuab energia muundurini.
Sellest, et peegeldumise vähendamine suurendab läbinud valguse hulka, on suhteliselt lihtne aru saada. Kui läbipaistvalt materjalilt, milles valgus ei neeldu, vähem valgust peegeldub, siis peab suurenema sellest materjalist läbi läinud valguse hulk, sest valgusenergia ei saa ju lihtsalt ära kaduda.
Kuidas aga peegelduse vähendamine aitab kujutist selgemaks teha? Alustame sellest, et täpsustame, mida tähendab selge kujutis. Kujutis on siis selge ehk hästi nähtav, kui tal on teravad piirjooned ja kujutis on piisavalt hele. Kujutame ette, et me tahame ekraanile projektoriga tekitada mingi pildi. Siis on mõistetav, et kujutis on seda heledam, mida vähem valgust objektiivi läätsede pindadelt tagasi peegeldub. Kuidas aga peegeldunud valgus muudab kujutise kontuurid ebateravaiks? See juhtub sellepärast, et peegeldumisel jaotub valgus ümber laiemaks kimbuks, mis ei anna enam teravat kujutist. Olukord on sarnane joonestamisega: kui tahetakse hästi täpset joonist teha, siis kasutatakse väga teravat pliiatsit. Siis on täpselt näha, kust jooned kulgevad.
Valguse hajumist klaasitükist läbiminekul on kujutatud joonisel 3.21. Lihtsuse mõttes pole seal kujutatud läätse, vaid siledat klaasitükki.
Kui mõlemad klaasi pinnad on kaetud selgendavate katetega, siis kaovad ära peegeldunud lained 2 ja 3, mis lähevad mujale kui laine 1 (J.3.22).
Muidugi peab ütlema, et peegeldunud valguse osa pole just suur ja seetõttu pole suured ka segavad efektid. Puhtalt klaasi pinnalt peegeldub tagasi sellele risti langevast valgusest umbes 4%. Kui langemisnurk suureneb, siis suureneb ka peegeldunud valguse hulk.
Selgendava katte töö põhineb katte ülemiselt ja alumiselt pinnalt peegeldunud lainete vastandfaasi viimisel. Seda on võimalik teha, kui valida sobivalt katte aine murdumisnäitaja ja kihi paksus.
Kui lained 2 ja 3 on vastandfaasis, siis nad kustutavad teineteise ja selle võrra suureneb kattest läbi läinud valguse hulk (J.3.23). Sobiv katte paksus on samas suurusjärgus valguse lainepikkusega, seega väga väike. Varem olid selgendavad katted väga õrnad ja riknesid kergesti igasugusel mehaanilisel töötlemisel (näiteks lapiga pühkimisel), kuid nüüdisaegne tehnoloogia võimaldab teha väga vastupidavaid katteid.
Märgime, et õhukeste kilede erinevatelt pindadelt peegeldunud valguslainete interferentsiga seletatakse ka seebimullide või putukatiibade värvusi.
Holograafia leiutas 1947. aastal Ungari päritolu füüsik Dennis Gabor, kes sai selle eest 1971. aastal Nobeli füüsikapreemia. Hologrammile nime andes lähtus D. Gabor kreeka keelest, kus "holos" tähendab täielik ja "gramma" – üleskirjutus. Seega tähendab "hologramm" täielikku üleskirjutust.
Mis aga on hologramm ja kuidas teda tehakse? Hologramm on holograafilisel meetodil saadud kolmemõõtmeline ehk ruumiline kujutis. Holograafia on esemete ruumilise kujutise fotograafiline jäädvustamine. Selle tulemusena saadakse esemest ruumiline pilt, mida nimetatakse hologrammiks ja mis põhimõtteliselt erineb nii tavalisest fotost kui ka 3D-kinos esitatavast ruumilisest elamusest.
Fotol jäädvustatakse esemete tasapinnaline, mitteruumiline kujutis. Tähtis on tähele panna, et fotografeerimisel me salvestame valguse E-vektori ruudu keskväärtuse, aga kogu info valguslainete faasi kohta läheb paratamatult kaduma. Fotot vaadates tekib küll mingi ruumilisuse mulje, sest harilikult on fotol meile tuttavad asjad ja neid me oskame omale ette kujutada. Ruumilisuse muljet aitavad tekitada perspektiiv, samuti varjud fotol. Põhiline erinevus foto ja hologrammi vahel seisneb selles, et fotol pole võimalik näha mingi eseme taga olevat teist eset, aga hologrammil on. Selleks tuleb ainult pead liigutada, et vaadata hologrammi teisest suunast.
3D-filmis ruumilise elamuse tekkimise põhimõtet tutvustame punktis 3.4.2 .
Vaatame lähemalt hologrammi valmistamist fotograafilisel meetodil ehk holografeerimist. Mingi eseme holografeerimiseks kasutatakse kahe koherentse kiirtekimbu interferentsi. Nende kimpude saamiseks kasutatakse kõigepealt kaht kumerläätse, mille abil muudetakse kitsas laserikiir laiaks paralleelsete lainete kimbuks. Üks osa sellest kimbust, nn tugikimp, suunatakse peegliga enne holografeeritava esemeni jõudmist fotoplaadile või -filmile (J.3.24)
Teine osa suunatakse sinna pärast holografeeritavalt esemelt peegeldumist. See on esemekimp.
Tugikimbus olevad lained jõuavad kõik fotoplaadini samas faasis, sest tegemist on tasalainega (paralleelne kimp). Esemekimp ei ole aga enam tasalaine – esemelt peegeldudes sisaldab selle lainefront kogu informatsiooni eseme väliskujust. Fotoplaadil kimbud kohtuvad ja interfereeruvad, sest laserivalgus on koherentne. Tulemuseks on keerulise kujuga interferentspilt, milles kajastub eseme ruumiline kujutis. Selgub, et sellises interferentsipildis on olemas ka info valguse E-vektori faasi kohta.
See pilt salvestatakse fotograafiliselt ja hologramm ongi valmis.
Hologrammi vaatamiseks kasutatakse ainult tugikimpu, st laiaks muudetud laserikiirte kimpu. See kimp suunatakse hologrammile, kus toimub valguse difraktsioon. Et hologrammis on salvestatud ka informatsioon valguse ajalise käitumise kohta, siis tekib täpselt samasugune lainekimp, nagu oli esemekimp. Kui seda kimpu vaadata, siis näeme esemega sarnast kujutist (J.3.25). Tekkinud kujutis on ruumiline.
Hologrammil on fotoga võrreldes mitmeid erinevaid omadusi:
- lihtne on koopiate tegemine, sest pole erinevust positiivi ja negatiivi vahel;
- purunemisel säilib igal tükil tervikpilt, sest valmistamisel pole kasutatud koondavat optikat ja kõik hologrammi osad sisaldavad infot kõigi originaali osade kohta;
- ühele fotoplaadile saab jäädvustada palju hologramme, piisab, kui näiteks iga kord enne holografeerimist fotoplaati pisut pöörata;
- kujutise suurust saab muuta, kui muuta vaatamisel kasutatava laseri lainepikkust: mida suurem lainepikkus, seda suurem kujutis.
| Hologramm hiirest. Seda hologrammi on pildistatud kahest suunast. Nagu näeme, erinevatest suundadest paistab pilt erinev, ruumiline info on hologrammi salvestatud. | Holograafia on väga võimas meetod ka teistsugustes kehade ruumilist kuju uurivates ülesannetes. Sellel pildil on näeme interferentsimustris kohti, kus kitarr rohkem võngub. |
Oleme seni rääkinud objektide ruumilise kuju üleskirjutamisest, aga valguslainete abil saab teha veel palju rohkem. Nii on interferentsinähtuse abil võimalik üles kirjutadada ka esemete liikumist, st põhimõtteliselt on võimalik hologrammi salvestada liikuvat ruumilist pilti sisaldav film. Selliste teemadega tegeleb nn. aegruumiline ehk 4D holograafia. Aegruumilise holograafia võimalikkuse tõestasid 1983. aastal Eesti TA Füüsika Instituudi (tänane TÜ Füüsika Instituut) teadlased akadeemik Peeter Saari juhtimisel.
Aga kui see kõik nii hea ja võimas on, miks me siis endiselt kasutame fotograafiat ja 2D videosid, selle asemel, et salvestada elu kogu oma täiuses? Põhjused on ühtaegu tehnilised ja põhimõttelised. Näiteks on üsna lihtne aru saada, et esemete ruumilise kuju üleskirjutamine tähendab rohkem informatsiooni ning holografeerimisel tuleb see ka kusagile üles kirjutada ja see tähendab suurema pikslite arvuga salvestus- ja esitlusseadmete kasutamist. Kui suure lahutusega fotoaparaatide tegemine ei ole täna põhimõtteliselt probleem, siis kättesaamatuks jääb holografeerimiseks tarvilik piksli suurus - ca poole mikromeetrilise serva pikkusega piksleid ei ole täna võimalik valmistada. Nii et ainus võimalus on kasutada vanamoodsaid fotoplaate. Vist isegi põhimõttelisem probleem on see, et igapäevaste olukordade holografeerimiseks on vaja kasutada üsnagi spetsiifilist laserivalgust.
Viimastel aastatel on aga tekkinud tehnika arengus uued suunad, mis annavad lootust, et vahepeal unustusehõlma vajunud tõeliselt ruumilise kino idee uuesti ellu ärkab. Nimelt on võimalik hologramme ka arvutada, kui on teada holografeeritavate objektide täpne kuju. 3D-animatsioonides on see info olemas, ainsaks põhimõtteliseks probleemiks jääb videoprojektorite lahutusvõime, mis peaks olema tuhandeid kordi suurem.
Aga kuidas jääb reaalse elu holografeerimisega? Ka siin võib läbimurre tulla tänu järjest kasvavale arvutusvõimsusele - põhimõtteliselt on võimalik esemete täpne kuju välja arvutada, kui on olemas piisav hulk erinevatest rakurssidest tehtud fotosid. Tulevik näitab, kas ja millises suunas see seni realiseerumata võimalus edasi areneb.
| Hologramm ühest optika õppevahendite komplektist. Annab aimu, mis moodi sellised hologrammid reaalselt välja näevad ja kuidas neid vaadatakse - ülemises vasakus nurgas on laser, millest väljub hajuv kiirtekimp ja satub hologrammile. Võrdle joonisega 3.25. | Hologrammi valmistamise komplekti LitiHalo Kit tutvustav video. Vaata, kas tunned seal ära protsessi etapoid, mis ülalpool tekstis juba räägitud. |
Interferents
Interferentsiks nimetatakse lainete liitumist, mille tulemusena liitlaine amplituud võib suureneda või väheneda võrreldes liituvate lainete amplituudidega.
Koherentsed lained
Koherentsed on lained, millel on ühesugune lainepikkus ja mille faaside vahe ei muutu aja jooksul.
Difraktsioon, interferents ja valguse laineline iseloom
Difraktsioon ja interferents on otsesteks tõenditeks selle kohta, et valgus on laine.
Difraktsioonivõre
Difraktsioonivõre on seade, mis kujutab endast paljude paralleelsete pilude süsteemi. Difraktsioonivõret kasutatakse valguse lainepikkuse määramiseks ja liitvalguse koostise uurimiseks (spektraalanalüüsiks).
Olgu meil valgusvoog, kus kõikide lainete levimissuunad on omavahel paralleelsed. Vaatame otse sellele kimbule vastu ja kujutame ette, et me suudame näha iga laine E-vektori võnkumist. Siis me näeksime umbes sellist pilti, mis on toodud joonisel 3.26. Valguslaine E-vektor võib võnkuda igas sihis, sest üksikute lainete kiirgumine pole mitte mingil viisil kooskõlastatud. Selline on nn loomulik valgus.
Kui asetaksime sellise valguse teele seadme, mis laseb läbi ainult mingis kindlas sihis, näiteks vertikaalsihis võnkuvate E-vektoritega laineid, siis näeksime joonisel 3.27 kujutatud pilti. Sellist valgust nimetatakse polariseeritud valguseks.
Valgust polariseerivat seadet nimetatakse polaroidiks. Loomulik valgus polariseerub läbi polaroidi minnes sellepärast, et see laseb läbi ainult valguslaineid, mille E-vektor võngub mingis kindlas sihis või tasandis. Seda tasandit nimetatakse polaroidi läbilasketasandiks ehk polarisatsioonitasandiks. Kui mingi laine E-vektor ei võngu läbilasketasandis, siis see laine neeldub polaroidis kas osaliselt või täielikult. Kõik valguslained, mille E-vektor võngub risti läbilasketasandiga, neelduvad täielikult ja nende energia muutub polaroidi siseenergiaks. Olukord on mõneti sarnane sellega, kui tahate suuski toast õue viia. Siis tuleb uksest läbi minnes suuski püsti hoida, muidu jäävad need ukse piitade taha kinni ja ei saa toast välja.
Seda, kas valgus on polariseeritud või mitte, tehakse kindlaks ka polaroidi abil. Kui vaadata loomulikku valgust läbi polaroidi, siis polaroidi pööramine ümber vaatesuuna ei põhjusta valguse intensiivsuse muutust. Kui aga vaadata polariseeritud valgust, siis polaroidi pööramisel valguse intensiivsus muutub.
On kokku lepitud, et seda polaroidi, mis valgust polariseerib, nimetatakse polarisaatoriks, ja seda, mille abil tehakse kindlaks valguse polarisatsioon – analüsaatoriks.
Uurime lähemalt, kuidas muutub polariseeritud valguse intensiivsus, kui seda valgust vaadata läbi analüsaatori, mida pööratakse ümber vaatesihi. Selleks hoiame polaroidi ühes kindlas asendis ja vaatame sealt tulnud valgust läbi analüsaatori. Pöörame analüsaatorit ümber vaatesihi, näiteks vastupäeva, ühe täisringi. Olukorda aitab mõista joonis 3.28, kus on näidatud polarisaatori P ja analüsaatori A neli asendit.
Kui polarisaatori läbilasketasand on vertikaalne ja analüsaatori läbilasketasand on ka vertikaalne, siis on analüsaatorist väljunud valguse intensiivsus maksimaalne (olukorrad a ja c). Kui läbilasketasandid on omavahel risti, siis ei pääse valgus üldse analüsaatorist läbi (olukorrad b ja d). Seega ühe täisringi jooksul esineb kaks intensiivsuse I maksimumi ja kaks miinimumi.
Valguse intensiivsuse sõltuvust valguse polarisatsioonitasandi ja analüsaatori läbilasketasandi vahelisest nurgast seletatakse järgmiselt.
Langegu polariseeritud valgus analüsaatorile, mille läbilasketasand on vertikaalne ja mille E-vektor moodustab läbilasketasandiga nurga . Sel juhul saab analüsaatorit läbida ainult komponent (vt J.3.29.)
Kuna valguse intensiivsus , saame intensiivsuse avaldiseks
Selle seaduse avastas Prantsuse füüsik E. Malus 1808. aastal.
Valgus polariseerub mitmetes protsessides, näiteks peegeldumisel või valikulisel neeldumisel, nagu see toimub polaroidides.
Peegeldunud valguse polariseerumises saame veenduda, kui vaatame näiteks lauapinnalt või kilekaantelt peegeldunud valgust läbi analüsaatori. Kui seda pöörata ümber vaatlussuuna, siis mingis analüsaatori asendis kaob peegeldunud valgus. Kui aga vaadata mõnelt metallesemelt peegeldunud valgust, siis see ei kao analüsaatori pööramisel. Kuna laualakk ja kilekaaned on dielektrilisest materjalist, siis meie katse näitab, et peegeldumisel polariseerub ainult dielektrikutelt peegeldunud valgus.
Eriti ilmekalt tuleb erinev polarisatsioon esile autodelt peegeldunud valguse korral: aknaklaasid muutuvad polaroidi mõne asendi korral täiesti mustaks, aga metallosad säravad kogu aeg.
Polaroidprillid. Nagu eespool räägitud, polariseerub valgus dielektrikutelt peegeldumisel. Järelikult mere- või järveveelt peegeldunud päikesevalgus on polariseeritud. Sellepärast kasutataksegi mõnedes päikeseprillides silmade kaitseks klaasidele kantud polaroidkilesid. Need vähendavad oluliselt veepinnalt, lumelt või märjalt asfaldilt peegeldunud valguse tugevust (J.3.30). Sellepärast kasutavad polaroid-päikeseprille peamiselt kalamehed, mäesuusatajad või autojuhid. Teistel on nad rohkem edevuse asjad.
Polaroidprille kasutatakse ka 3D-filmide vaatamiseks.(J.3.31) 3D-filmi tegemisel kasutatakse filmimiseks kaht kaamerat üheaegselt. Kaamerad asuvad kõrvuti nagu meie silmadki. Filmi näitamisel kasutatakse kaht projektorit, millest üks näitab vasakpoolse kaameraga tehtud filmi ja teine parempoolse kaameraga tehtud filmi. Mõlemad projektorid on suunatud ekraani ühte kohta. Ruumilise kujutise tekkimiseks peab vaataja nägema vasaku silmaga vasakpoolse kaamera filmitut ja parema silmaga parempoolse kaameraga filmitut. Selle saavutamiseks kasutatakse projektorite ees ristiolevate läbilasketasanditega polaroide. Ka vaatajal on ees polaroidklaasidega prillid, mille vasaku klaasi läbilasketasand on sama mis vasakpoolsel projektoril ning parempoolsel sama mis parempoolsel projektoril.
Vedelkristall-kuvar. Vedelkristall-kuvareid (VK-kuvareid, inglise keeles LCD ehk Liquid Crystal Display) kasutatakse televiisorites ja arvutites pildi nähtavaks tegemiseks ehk kuvamiseks. Vedelkristall-kuvari põhiosad on ekraan pikslitega, valge taustvalguse allikas ja valguse hajutaja. Sellelt tulev valgus juhitakse ekraanile läbi pikslite, mis tekitavad soovitud pildi (J.3.32).Pikslid on on paigutatud kindlatesse ridadesse ja veergudesse ning igaüks neist laseb läbi kas punast, rohelist või sinist valgust. Neid värvusi kombineerides on võimalik saada igasuguseid värvitoone.
Piksli nimi tuleb ingliskeelsetest sõnadest picture ja element, seega eesti keeles oleks nimi pildielement.
Pikslid on imeväikesed, palja silmaga eristamatud. Iga piksel koosneb klaasplaatide vahele pandud vedelkristallist (J.3.33). Plaatide pinnad on kaetud polaroidkile ja kas punase, rohelise või sinise valgusfiltriga (ainega, mis laseb läbi ainult vastavat värvi valgust). Kummalgi pinnal on ka läbipaistvast materjalist elektrood, mis lubab tekitada pikslis elektrivälja. Piksli pindadel olevate polaroidide läbilasketasandid on omavahel risti ja pingestamata elektroodide korral valgus pikslit ei läbi. Selline piksel paistab ekraanil musta täpina.
Pikslis olev vedelkristall on aine, mis on vedel, aga millel on kristallidele omane struktuur. Elektriväljas muutub vedelkristall optiliselt aktiivseks – teda läbiva polariseeritud valguse võnketasand pöördub. Pingestatud pikslis ei ole polaroidide läbilasketasandid enam omavahel risti ja pikslist hakkab valgus läbi minema. Polarisatsioonitasandi pöördenurk oleneb kasutatud pinge suurusest. See võimaldab muuta pikslit läbinud valguse hulka. Nii saame tekitada ekraanile erineva heleduse ja värvusega punkte, mis kokku annavad soovitava värvilise kujutise.
Loomuliku valguse polarisatsioon
Loomulikus valguses võivad valguslainete E-vektorid võnkuda suvalises sihis.
Polariseeritud valgus
Polariseeritud valguses on kõikide lainete E-vektorite võnketasandid paralleelsed.
Polaroid töötab
Kui polariseeritud valgust vaadata läbi polaroidi, siis polaroidi keeramisel umber vaatesuuna muutub valguse intensiivsus.
Niisiis, kui salvestada objektist erinevate nurkade alt piisav hulk fotosid, siis peaks arvuti olema põhimõtteliselt võimeline sellest kokku panema hologrammi, ehk selle objekti täieliku ruumilise üleskirjutuse. Teisalt... meil on ju vaid kaks silma, kas on mõtet luua salvestust, mille täielikuks nautimiseks peaks meil olema tuhat silma?
Arvatavasti me kõik oleme lugenud vähemasti ühte muinasjuttu, kus peategelasel õnnestub enesele hankida nähtamatuks tegev mantel... tavaliselt on tal sellest ka palju kasu. Muidugi selliseid mantleid ei ole "päriselt olemas"... või ikkagi on?
Sest lõpuks ei ole asi mantlis vaid selles, mida vaataja näeb või ei näe. Ja kui me teame, mismoodi käitub ja tekitab valgusaistinguid see osa elektromagnetlainetest, mida me valguseks nimetame, siis me saame ka öelda, kas ja mis võiks põhimõtteliselt võimalik olla. Ja siis oskame me ka arvata, kas nähtamatu mantel on põhimõtteliselt võimalik ning kas siin pildil olev tee on ikka kindlasti tühi.
Me alustame valguse ja aine vastastikmõju uurimist põhikoolis õpitud geomeetrilise optika seadustest ning läheme siis järk-järgult üle keerulisematele nähtustele.
Geomeetriline optika on optika osa, kus valguslaine asemel kasutatakse valguskiire mõistet. Valguskiireks nimetatakse joont ruumis, mis näitab valgusenergia levimise suunda. Geomeetrilist optikat nimetatakse ka kiirteoptikaks.
Loobumist valguse laineomadustest saab kasutada juhtudel, kui avad või tõkked valguse teel on palju suuremad valguse lainepikkusest. Sel juhul ei ole vaja arvestada difraktsiooni, mis sunnib valgust tõkete taha levima.
Geomeetrilise optika põhiseadused on:
- Valguse sirgjoonelise levimise seadus: ühtlases keskkonnas levib valgus sirgjooneliselt.
- Kiirte sõltumatuse seadus: kiired ei mõjuta lõikumisel üksteise liikumist.
- Valguse peegeldumise seadus: langemisnurk ja peegeldumisnurk on võrdsed.
- Valguse murdumise seadus: langemisnurga ja murdumisnurga siinuste suhe on jääv suurus.
- Kiirte pööratavuse printsiip: kiir läbib süsteemi päri- ja vastassuunas ühte teed mööda.
Ühtlases keskkonnas levib valgus sirgjooneliselt. Kui aga valguse teele jääb ette mingi keha või läheb valgus üle teise keskkonda, siis valguse levimissuund muutub. Esimesel juhul räägitakse valguse peegeldumisest, teisel juhul valguse murdumisest. Läbipaistvate kehade korral esinevad mõlemad nähtused korraga.
Kui pind on sile, siis jääb paralleelne kiirtekimp nii peegeldudes kui murdudes paralleelseks.
Kui pind ei ole sile, siis paralleelne kiirtekimp ei jää paralleelseks ei peegeldumisel ega murdumisel. Sel juhul kiirtekimp läheb "segamini", mille kohta öeldakse, et valgus hajub.
Aga milline pind on sile? Füüsikud on kindlaks teinud, et pinda võib siledaks lugeda, kui pinna konaruste mõõtmed on väiksemad kui valguse lainepikkus. See tähendab, et pinnal ei või olla muhkusid ja lohke, mille sügavus on suurem kui umbes 100 nm ehk kümnetuhandik millimeetrit.
Aga alati ei pea sile peegel olema nii väikeste konarustega. Vaadake või TV paraboolantenne. Need pole sugugi väga siledad. Aga tegelikult on konarused palju väiksemad antennile langevate elektromagnetlainete lainepikkusest, mis on detsimeetri suurusjärgus
Optiliste pindade valmistamine on alati olnud keeruline ja kallis töö, aga Eestil on selles vallas oma suurmees ette näidata. Bernhard Schmidt (30. märts 1879 – 1. detsember, 1935) on Eestist pärit optik, kes suutis valmistada suuri läätsi ja peegleid täpsemalt, kui ükskõik missugune tolleaegne suur tehas. Kusjuures ta tegi seda vaid ühe käega - teise käe kaotas ta lapsepõlves lõhkeainetega katsetades. B. Schmidt konstrueeris ka astronoomia ja teleskoopide arengus täiesti uue kvaliteedi loonud teleskoobid, mida nüüd nimetatakse Schmidt'i teleskoopideks.
Kõik me oleme ennast peeglist vaadanud. Aga kus meie kujutis asub? Kas see on nagu pilt raamis või on ta peegli ees või taga? Füüsikas nimetatakse tasku- või seinapeeglit tasapeegliks. Seega on meil vaja lahendada ülesanne sellest, kus asub eseme kujutis tasapeegli korral. Sellele küsimusele saame vastuse, kui leiame joonise abil kujutise asukoha tasapeeglis.
Asugu punktikujuline ese punktis A (J.4.4). Selle kujutise asukoha leidmiseks võtame punktist A kaks kiirt AO ja AB. Kuna kiir AO langeb peeglile risti, siis peegeldub ta ka ristsuunas tagasi. Kiir AB peegeldub vastavalt peegeldumisseadusele (). Peegeldunud kiired hajuvad, ei lõiku omavahel. Järelikult tekib näiv kujutis. Kui me neid hajuvaid kiiri ülalt vaatame, siis näeme, nagu kiired väljuksid peegli taga asuvast punktist A1. Seal asubki punkti A näiv kujutis.
Järelikult tekib kujutis tasapeegli taha. Aga kui kaugel peegli taga kujutis on?
Sellele küsimusele saame vastuse, kui vaatleme kolmnurki AOB ja A1OB. Neil kolmnurkadel on üks ühine külg ja selle lähisnurgad AOB ja A1OB ning ABO ja A1BO on võrdsed. Järelikult on ka kolmnurgad võrdsed ja AO = A1O. See tähendab, et punkti A näiv kujutis tekib peegli taha samale kaugusele, kui suur on punkti A kaugus peeglini.
Järelikult pole ka meie peeglis nähtav kujutis mitte peeglis, vaid peegli taga.
Kui valguskiir läheb ühest keskkonnast teise, siis kiire suund muutub. Sellist nähtust nimetatakse valguse murdumiseks. Valguse murdumise põhjuseks on valguse kiiruse muutumine üleminekul teise keskkonda.
Olukorra mõistmiseks kujutame ette olukorda, kus veerev käru liigub asfaldilt põiki pehmele murule. Mis juhtub? Käru muudab oma liikumissuunda, sest ühed rattad jõuavad murule enne kui teised ja murul veerevad rattad halvemini kui asfaldil (J.4.5).
Sarnane on olukord ka valguse üleminekul ühest keskkonnast teise. Vaatleme tasalaine üleminekut õhust vette.
Ka nüüd hakkab see osa lainefrondist, mis jõuab vette liikuma aeglasemalt kui õhus liikuv lainefrondiosa. Selle tulemusena muutub ka lainefrondi ristsirge ehk kiire levimise suund.
Valguse murdumist kasutatakse kõige rohkem läätsedes, kuid palju kasutatakse ka prismasid, mis on tähtis optiline detail mitmetes optikariistades nagu spektromeeter või monokromaator.
Prismaks nimetatakse läbipaistvast materjalist keha, millel on tavaliselt paralleelsed kolmnurksed põhjad (joonisel 4.7) lehekülje tasandiga paralleelsed) ja servad on risti põhjadega.
Prismat iseloomustavad põhilised suurused on murdev nurk ja alus. Nurka prisma tahkude vahel, kuhu valgus langeb ja kust väljub, nimetatakse prisma murdvaks nurgaks. Tahku murdva nurga vastas nimetatakse prisma aluseks.
Langegu klaasprismale valguskiir õhust nurga all. Prismasse minnes kiire suund muutub nii, et murdumisnurk on väiksem langemisnurgast. Kui kiir jõuab teise tahuni, siis on langemisnurk ja väljumisel prismast on murdumisnurk suurem langemisnurgast. Prismast väljunud valgus kaldub alati prisma aluse poole.
Vala purki vett. Pane pliiats purgi keskel vertikaalselt püsti. Vaatle pliiatsit. Milline tundub olevat pliiats? Liiguta pliiatsit enda poole ja endast eemale (ette-taha). Mida Sa näed? Liiguta pliiatsit paremale- vasemale (vt ülemine joonis). Mida Sa näed?
Võib-olla märkasid ka seda, et pliiatsi liigutamisel vasakult paremale liigub kujutis purgis mööda kaart. Purgi keskel on kujutis Sinust kaugemal, äärtel aga lähemal. Miks see nii on, selgub alumiselt jooniselt.
Pliiatsilt lähtuvad kaks valguskiirt jõuavad silma hajuvate kiirtena. Kujutis tekib aga seal, kus valguskiirte pikendused lõikuvad. Nagu jooniselt näha lõikuvad kiirte pikendused eseme asukohast eespool. Seepärast tundubki kujutis olevat eespool kui ese.
Aga miks paistab pliiats vees paksem kui õhus? Põhjuseks on kumer purk, mis töötab selles katses nagu lääts.
Põhikoolis tutvusime valguse murdumise seaduspärasustega. Nüüd saame teada seaduse, mille kohaselt murdumine toimub. Alustuseks tuletame meelde, kuidas oleneb valguse murdumisel murdumisnurk langemisnurgast
Katsetest näeme, et langemisnurga suurenedes suurenes ka murdumisnurk ja langemisnurga vähenedes vähenes ka murdumisnurk. Nurkade väärtused olid alati erinevad, välja arvatud olukord, kui langemisnurk oli null kraadi, siis oli null kraadi ka murdumisnurk. Lihtsamalt öelduna: kui valgus langeb pinnale risti, siis murdumist ei ole ja kiir levib edasi samas suunas mis ennegi.
Milline on aga seos langemis- ja murdumisnurkade vahel? Selle seose avastas Hollandi astronoom ja matemaatik Willebrord Snellius, kes 1621. aastal sõnastas valguse murdumisseaduse: valguse üleminekul ühest keskkonnast teise on langemisnurga ja murdumisnurga siinuste suhe jääv suurus
Seda konstanti nimetatakse murdumisnäitajaks. Kui keskkond, kust valgus tuleb, on vaakum, siis on tegemist absoluutse murdumisnäitajaga . Teistel juhtudel on tegemist suhtelise murdumisnäitajaga .
Eespool nägime, et valgus ei murdu üleminekul ühest keskkonnast teise, kui langemisnurk on null kraadi. Nähtusele saame seletuse murdumisseadusest. Avaldame murdumisnurka sisaldava suuruse
Nüüd on näha, et kui langemisnurk , siis ka , järelikult ka ning seega ka murdumisnurk . See tähendabki, et kiir oma levimissuunda ei muuda.
Absoluutne murdumisnäitaja iseloomustab ainet samuti nagu selle tihedus või eritakistus. Absoluutne murdumisnäitaja oleneb valguse levimise kiirusest antud aines ja vaakumis :
Nagu valemist näha, on absoluutne murdumisnäitaja ilma mõõtühikuta suurus ja näitab, kui palju on valguse kiirus vaakumis suurem kui antud aines.
Valguse kiirus on vaakumis 3·108 m/s ja vees 2,25·108 m/s. Järelikult vee absoluutne murdumisnäitaja
|
Aine |
n |
|
Õhk |
1,0003 |
|
Vesi |
1,33 |
|
Klaas (erinevad sordid) |
1,4 ... 1,6 |
|
Teemant |
2,42 |
Kui valgus tuleb vaakumist ja läheb mingisse keskkonda, siis murdumisseadust saab kirjeldada järgmise valemiga:
Aine absoluutse murdumisnäitaja määramine on oluline mitmes eluvaldkonnas. Näiteks optiliste materjalide valmistamisel läätsede, selgendavate katete või optliste valgusjuhtide tarbeks.
Murdumisnäitaja mõõtmist kasutatakse laialdaselt nii jookides (mahlad, veinid) kui tehnilistes vedelikes (jahutusvedelikud, tulekustutusvahud) sisalduvate ainete kontsentratsiooni määramiseks. Näiteks mees sisalduva veehulga määramiseks kasutatakse samuti mee murdumisnäitaja mõõtmisi.
Klaasi murdumisnäitajat saad ka ise mõõta. Selleks aseta klaastahukas lehele ja joonista lehele väga täpselt klaasi piirjooned. Torka kaks nööpnõela ühele poole tahukat nii, et üks on klaasi vastas ja teine kaugemal (~5 cm), nii et neid ühendav sirge kujutaks keskmise langemisnurgaga valguskiirt.
Vaatle läbi klaastahuka teiselpool asuvaid nööpnõelu ja torka kaks nööpnõela paberisse nii, et kõik neli paistaksid asuvat ühel sirgel (vaata fotot). Tegelikult ei asu nööpnõelad ühel sirgel, vaid moodustavad murdjoone, mis vastab valguskiire levimisele. Võta klaastahukas jooniselt, märgi ja mõõda vajalikud nurgad (vaata joonist) ja arvuta murdumisnäitaja .
Suhteline murdumisnäitaja on määratud kahe keskkonna absoluutsete murdumisnäitajate suhtega. On kokku lepitud, et suhteline murdumisnäitaja näitab teise keskkonna absoluutse murdumisnäitaja suhet esimese keskkonna absoluutsesse murdumisnäitajasse. Esimeseks keskkonnaks nimetatakse seda keskkonda, kust valgus tuleb ja teiseks seda, kuhu valgus läheb.
Seega kahe keskkonna suhteline murdumisnäitaja
kus ja , kusjuures ja on vastavalt valguse kiirused teises ja esimeses keskkonnas.
On võimalik leida ka seos suhtelise murdumisnäitaja ja valguse kiiruste vahel erinevates keskkondades:
Siit on näha, et kahe keskkonna suhteline murdumisnäitaja näitab, mitu korda on valguse kiirus esimeses keskkonnas suurem kui teises.
Näiteks mingu valgus klaasist vette. Siis on vee suhteline murdumisnäitaja klaasi suhtes
Kui aga valgus läheb veest klaasi, siis
Ainete suhtelised murdumisnäitajad õhu suhtes on praktiliselt võrdsed nende ainete absoluutsete murdumisnäitajatega, sest õhu absoluutne murdumisnäitaja on küllalt suure täpsusega võrdne ühega.
Optikas me nimetame läätseks läbipaistvat keha, mille pindadeks on kõverpinnad. Meie käsitleme ainult sfäärilisi läätsi, mille korral pindadeks on kahe kerapinna osad. Tavaliselt kasutatakse läätsesid, mille pindade raadiused on võrdsed, st (J.4.11).
Tuletame lühidalt meelde olulisemad aspektid põhikoolis läätsede kohta õpitust.
Sirget, mis läbib nende kerade keskpunkte, nimetatakse läätse optiliseks peateljeks. Kõik teised sirged, mis läbivad läätse keskpunkti, on optilised teljed.
Läätsi liigitatakse kumer- ja nõgusläätsedeks. Kumerläätsed on keskelt paksemad kui äärest. Nõgusläätsed on keskelt õhemad kui äärest. Nõgusläätsest läbi minnes valguskiired hajuvad, sellepärast nimetatakse selliseid läätsi ka hajutavateks läätsedeks.
Kumerläätsele langevad optilise peateljega paralleelsed kiired lõikuvad pärast läätse läbimist punktis, mida nimetatakse läätse fookuseks (J.4.12, a). Nõgusläätse korral aga hajuvad läätsele langevad paralleelsed kiired nii, et nende pikendused lõikuvad ühes punktis, mida nimetatakse läätse näivaks fookuseks (J.4.12), b).
Fookusi läbivaid tasandeid, mis on risti optilise peateljega, nimetatakse fokaaltasanditeks.
Mis juhtub aga siis, kui läätsele langeb paralleelsete kiirte kimp, mis ei ole paralleelne optilise peateljega? Kumerläätse korral see kiirtekimp koondub fokaaltasandi punktis, mis on määratud läätse keskpunkti läbiva kiirega. Nõgusläätse korral selline kiirtekimp hajub nii, et kiirte pikendused lõikuvad fokaaltasandi punktis, mis on samuti määratud läätse keskpunkti läbiva kiirega (J.4.13).
Igal läätsel on kaks fookust või näivat fookust, mille kaugused läätse keskpunktist on võrdsed. Seda kinnitab ka kiirte pööratavuse printsiip, mille kohaselt kiirte käik läbi optilise süsteemi ei olene sellest, kas kiired liiguvad läbi läätse näiteks vasakult paremale või paremalt vasakule.
Fookuse või näiva fookuse kaugust läätse keskpunktist nimetatakse fookuskauguseks.
Fookuskauguse pöördväärtust nimetatakse läätse optiliseks tugevuseks , st
Läätse optilist tugevust mõõdetakse dioptriates(dptr), kusjuures 1 dioptria on sellise läätse optiline tugevus, mille fookuskaugus on 1 m. Kumerläätsede optilist tugevust loetakse positiivseks, nõgusläätsede oma negatiivseks.
Mida suurem on läätse optiline tugevus, seda rohkem lääts koondab või hajutab kiiri. Prilliklaaside tugevust kirjeldav arv pole midagi muud kui kasutatava läätse optiline tugevus dioptriates. Kui kellelgi on prillid –2,5, siis see arv ütleb meile, et tema prillides on nõgusläätsed, mille fookuskaugus on . Kumerläätsega saab esemest kujutist ekraanile tekitada, nõgusläätsega ei saa. Aga kui läbi nõgusläätse eset vaadata, siis me näeme seda.
Kujutist, mida on võimalik tekitada ekraanile, nimetatakse tõeliseks kujutiseks. Kujutist, mida me silmaga näeme, aga ekraanile tekitada ei saa, nimetatakse näivaks kujutiseks.
Tõeliste ja näivate kujutiste asukohti on võimalik leida graafiliselt, st joonise abil.
Kumerlääts koondab valguskiiri. Kujutise asukoha leidmiseks ehk kujutise konstrueerimiseks kasutatakse esemest väljuvatest kiirtest vähemalt kahte järgmisest kolmest (J.4.14):
- optilise teljega paralleelset kiirt, mis pärast läätse läbimist läheb läbi fookuse;
- fookust läbivat kiirt, mis pärast läätse läbimist on optilise teljega paralleelne;
- läätse keskpunkti O läbivat kiirt, mis pärast läätse läbimist suunda ei muuda.
Kuidas leida aga optilisel peateljel oleva punkti kujutise asukohta? Kujutise konstrueerimisel seda ei tehta. Eeldatakse, et kui ese asub risti optilise peateljega, siis on ka eseme kujutis risti optilise peateljega. Ja nii on ka õige. Aga mida teha siis, kui esemeks ongi punkt optilisel teljel?
Vaatleme, kuidas toimub sellise punkti kujutise leidmine kumerläätse korral (J.4.15). Sel juhul võtame etteantud punktist mingi suvalise läätse poole suunduva kiire, näiteks AC, ja joonistame sellele kiirele paralleelse kiire, mis langeb läätse keskpunkti O. Nüüd on meil kahekiireline paralleelne kiirtekimp, mis langeb läätsele kaldu. Selline kimp koondub fokaaltasandi punktis D. Järelikult sellest punktist läheb läbi ka punktist A väljunud ja läätsele punktis C langenud kiir.
Kujutise asukoha leidmiseks on vaja teada kahe esemest väljunud kiire lõikepunkti teisel pool läätse. Valime teiseks kiireks piki optilist peatelge liikuva kiire AO, mis läbib läätse keskpunkti. See kiir läätse läbimisel oma levimissuunda ei muuda ja levib ikka piki optilist peatelge.
Nii saamegi kujutise asukohaks punkti A1.
Nõguslääts hajutab valguskiiri. Kujutise konstrueerimiseks kasutatakse esemest väljuvatest kiirtest vähemalt kahte järgmisest kolmest (J.4.16):
- optilise peateljega paralleelset kiirt, mis pärast läätse läbimist läheb edasi nii, et selle pikendus läheb läbi näiva fookuse;
- tagumisse näivasse fookusse F1 suunatud kiirt, mis pärast läätse läbimist on optilise teljega paralleelne;
- läätse keskpunkti O läbivat kiirt, mis pärast läätse läbimist suunda ei muuda.
Leiame kumerläätse jaoks avaldise, mis seob omavahel eseme ja läätse keskpunkti vahelise kauguse ehk esemekauguse , tekkiva kujutise ja läätse keskpunkti vahelise kauguse ehk kujutisekauguse ja läätse fookuskauguse .
Lähtume kolmnurkade AOB ja A1OB1 sarnasusest (J.4.17). Need kolmnurgad on sarnased sellepärast, et neil on võrdsed nurgad. Järelikult on võrdsed ka nende vastavate külgede suhted
Fookuskauguse sissetoomiseks vaatame kolmnurki COF ja B1A1F. Ka need on sarnased. Saame
Valem (4.5) aga andis meile, et
Seega
Jooniselt 4.17 on näha, et ja , siis
nii et
Jagame võrrandi mõlemaid pooli suurusega ja saame:
Saadud valemit nimetataksegi läätse valemiks. Sellisel kujul on valem õige tõelise kujutise korral.
Näiva kujutise korral on kujutisekaugus negatiivne ja valemi kuju on
Kui kujutis on näiv ja ka fookuskaugus on näiv, siis on nii kui negatiivsed ja valemi kuju on
Selline on valemi kuju nõgusläätse jaoks.
Läätse valem lubab teha järeldusi kujutise asukoha kohta olenevalt eseme asukohast. Vaatleme kolme juhtu kumerläätse korral.
- Asugu ese läätse fookuses, st , siis läätse valem 4.6 omandab kuju Siit saame, et , st on lõpmatus. Seega juhul, kui ese asub läätse fookuses, tekib kujutis lõpmatuses. See tähendab, et läätsest väljuvad paralleelsed kiired.
- Asugu ese lõpmatuses, siis . See järeldus tuleneb eelmisest tulemusest, kui kasutada kiirte pööratavuse printsiipi. Seega juhul, kui läätsele langevad paralleelsed kiired, tekib kujutis läätse fookuses.
- Asugu ese läätsele lähemal kui fookuskaugus, st . Kujutisekauguse leidmiseks avaldame selle läätse valemist (4.6) Siit Kuna nii kui on positiivsed ja , siis peab . Seega juhul, kui ese asub läätse ja selle fookuse vahel, siis on kujutisekaugus negatiivne, mis tähendab, et tekib näiv kujutis.
Läätse poolt tekitatud kujutis võib olla nii suurendatud kui vähendatud. Selle kirjeldamiseks kasutatakse suurenduse mõistet, täpsemalt joonsuurendust, mis näitab, mitu korda erinevad kujutise mõõtmed eseme vastavatest mõõtmetest.
Näiteks joonisel 4.17 on suurendus . Kuid valemist (4.5) näeme, et . Seega suurendus
Siit on näha, et kui , siis , st kujutis on sama suur kui ese. Läätse valemist on näha, et sel juhul
See tähendab, et koondava läätse korral on kujutis sama suur kui ese siis, kui esemekaugus on võrdne kahekordse fookuskaugusega.
Teisi järeldusi suurenduse kohta võib teha kas valemeid analüüsides või kujutisi konstrueerides. Toome ära mõned kasutamise seisukohast olulisemad tulemused.
- Kui , siis on , mis tähendab, et kujutis on esemest väiksem.
- Kui , siis , mis tähendab, et kujutis on esemest suurem.
- Kui , siis tekib suurendatud näiv kujutis ja öeldakse, et lääts töötab siis luubina.
- Nõgusläätse korral on alati , mis tähendab, et nõguslääts annab alati vähendatud näiva kujutise
Iga lääts võib töötada luubi ehk suurendusklaasina Tavaliselt kasutatakse selleks läätsi, mille optiline tugevus jääb vahemikku 10…40 dptr. See tagab suurenduse 2,5×…10×. Suuremate suurenduste saamiseks kasutatakse mikroskoope.
Koondav lääts töötab luubina, kui ese asub läätsele lähemal kui selle fookuskaugus.
Luup annab esemest päripidise suurendatud näiva kujutise.
Tavaliselt asetatakse ese praktiliselt luubi fookusesse. Sel juhul on luubi suurendus määratud järgmise valemiga:
kus on parima nägemise kaugus ja luubi fookuskaugus. Parima nägemise kauguseks loetakse 25 cm ja sellepärast peame suurenduse valemis kasutama ka läätse fookuskaugust sentimeetrites.
Kasutades joonist 4.18, tuletame luubi suurenduse valemi.
Luubi suurendus näitab, mitu korda on luubiga vaadates kujutis meie silmas suurem kui palja silmaga vaadates,
seega
Kui silma põhja kujutise piirkonnas lugeda tasandiks, siis saame sarnastest kolmnurkadest ABO1 ja A1B1O1 joonise 4.18 a) osas:
Teistest sarnastest kolmnurkadest ABO ja A2B2O1 joonise b) osas saame:
Silm on mõlemal juhul ühesugune, seega . Nüüd saame
Geomeetrilise optika põhiseadused
Geomeetrilise optika põhiseadused on valguse sirgjoonelise levimise seadus, kiirtekimpude sõltumatuse seadus, peegeldumise seadus, murdumise seadus ja kiirte pööratavuse printsiip.
Lahendus
Kujutis jääb alles, aga on poole tuhmim - pooled valvguskiired ei jõua ekraanile.
Juba mõnda aega enne Newtoni eksperimente teati, et prismast läbi minevast valgest valgusest tekib palju erineva värvusega valgusi. Aga enne Newtonit arvati, et prisma "värvib" valge valguse vikerkaarevärviliseks, nagu näiteks punane klaas "värvib" valge valguse endast läbi lastes punaseks.
Newton kummutas sellise arvamuse, lastes kord juba prismast läbikäinud valgusest ainult üht värvi valguse läbi teise prisma ja sellega ei juhtunud enam midagi. Sellest katsest tegi Newton järelduse, et valge valgus on liitvalgus, mis koosneb paljudest värvilistest valgustest, mida on üksteisest võimalik prisma abil eraldada.
Tänapäeval on teada, et värviliste valguste eraldumine üksteisest on tingitud dispersioonist, milleks nimetatakse aine absoluutse murdumisnäitaja sõltuvust valguse sagedusest või lainepikkusest. Mida väiksem on valguse lainepikkus, seda suurem on sellele vastav murdumisnäitaja. Sellepärast kalduvadki prismast läbiminekul kõige rohkem kõrvale violetne ja sinine valgus ja kõige vähem punane valgus.
Dispersiooni jälgimiseks tarviliku prisma saame ka ise valmistada, näiteks kaldu vette asetatud peeglist, millele valgust juhtides võime laes saada vikerkaarevärve.
Dispersioon on erinevates ainetes erineva suurusega, kuid murdumisnäitajate erinevused nähtava spektripiirkonna ulatuses on küllalt väikesed, mitte üle mõne protsendi. Sellest aga piisab, et valgest valgusest kõik vikerkaarevärvid välja meelitada.
Tüüpiline murdumisnäitaja sõltuvus valguse lainepikkusest, nn dispersioonikõver, on toodud joonisel 4.20.
Valguse dispersiooniga peab arvestama praktiliselt kõigi optiliste seadmete konstrueerimisel. Näiteks dispersioon läätsedes põhjustab kujutise moonutusi (J.4.21). Põhjus on selles, et läätse materjal murrab erineva lainepikkusega valguslaineid erinevalt. Sinise valguse lained murduvad läätses rohkem kui punase valguse lained ja sellepärast on fookus sinise valguse jaoks läätsele lähemal kui punase valguse jaoks. Tulemuseks on kujutise teravuse ja värvuste moonutumine. Seda nähtust nimetatakse kromaatiliseks aberratsiooniks, mida võib eesti keelde tõlkida kui värviline moonutus.
Looduses on dispersiooniga seletuv ilus taevane värvidemäng – vikerkaar.
Vikerkaart võib taevas näha siis, kui üheaegselt paistab päike, kuskil sajab vihma ja meie oleme päikese ja vihmapilve vahel, nii et päike jääb meie seljataha. Vikerkaart võib näha ka purskkaevu või muruniisuti piiskades.
Taevas on vikerkaar kõige kõrgem kas hommikul või õhtul, siis kui päike on madalal. Suvisel keskpäeval, kui päike on horisondist kõrgemal kui 42°, ei ole vikerkaar nähtav, sest ta jääb silmapiirist madalamale.
Vikerkaare tekkimisest arusaamiseks on joonisel 4.22 kujutatud päikesevalguse murdumine ja peegeldumine kahes piisas ja vikerkaare nägemine.
Jälgime vihmapiisa ülaosast sisenenud päikesevalguse teed piisas a. Osa piisale langevast valgusest peegeldub selle välispinnalt (pole joonisel näidatud). Ülejäänud osa läheb piiska ja murdub vees, kusjuures sinine valgus murdub rohkem kui punane valgus. Jõudes piisa tagaküljeni, osa valgust väljub piisast (pole joonisel näidatud) ja osa peegeldub piiska tagasi. Jõudes piisa esiküljeni osa valgust peegeldub piiska tagasi (pole joonisel näidatud) ja osa murdub õhku.
Sarnaselt käitub valgus igas piisas ja me näemegi vikerkaart, sest piisku on palju ja valgus siseneb piiskadessse mitte ainult selle ülaosast, vaid igast kohast. Igale värvusele vastab kindel nurk horisontaalsihi suhtes, kust valgus meie silma jõuab. See nurk ei pea olema just vertikaaltasandis, vaid võib olla suvalises tasandis.
Mõnikord on võimalik näha ka teist vikerkaart, mis on esimese kohal ja kus on värvused vastupidiselt madalamal oleva vikerkaarega (punane äär on allpool kui sinine). Selline vikerkaar tekib siis, kui me näeme ka neid kiiri, mis on sisenenud tilga alaosast (vaata joonist 4.22 b ja 4.23) ja peegeldunud tilgas enne väljumist kaks korda. Kuna igal peegeldumisel valguse intensiivsus väheneb, siis on nn teist järku vikerkaar palju nõrgem põhivikerkaarest ja on nähtav ainult väga tugeva vihma korral, kui piisku on palju. Ka päike peab selgelt paistma.
Kõrgemat järku vikerkaared on ka olemas, näiteks laboris on saadud kolmteist vikerkaare järku. Aga looduses pole lootust neid näha, sest nad on väga nõrgad ja mõned (näiteks 3. järku vikerkaar) tekivad päikese ümber, kust on neid võimatu näha heleda päikesevalguse taustal.
Esimesena uuris valge valguse koostist teaduslikult I. Newton 1666. aastal. Ta laskis aknakardinasse tehtud väikesest august päikesevalguse prismale ja sealt toa seinale. Sinna tekkinud vikerkaarevärvides riba nimetaks ta spektriks. Nimi tuleneb ladina keelsest sõnast spectrum, mis eesti keeles tähendab nägemust või kujutluspilti. Hiljem on hakatud spektriks nimetama diagrammi, mis näitab valguse intensiivsuse jaotumist lainepikkuste või sageduste järgi.
Tänapäeval saab spektreid vaadata igaüks, kasutades selleks kõigile kättesaadavaid difraktsioonivõresid – DVD või CD plaate. Joonisel 4.24 kujutatud eksperimendis on näha küünlaleegi spektrit.
Spektri saamiseks, jälgimiseks ja mõõtmiseks kasutatakse spektraalriistu. Neid võib jaotada kahte gruppi: spektromeetriteks ja spektroskoopideks.
Spektromeeter (kr metreo – mõõdan) on riist spektrite mõõtmiseks, st erineva lainepikkusega valguse intensiivsuse määramiseks.
Spektroskoop (kr skopeo – vaatlen) on riist spektrite vaatlemiseks.
Vaatleme lähemalt prismaspektroskoobi ehitust (J.4.25). Uuritav valgus suunatakse spektroskoopi läbi kitsa pilu, mille laius on suurusjärgus 0,1 mm. Pilu asub läätse 2 fookuses ja läätsest väljub paralleelne kiirtekimp, mis suunatakse prismale 3.
Prismas toimub valguse dispersioon, s.t. erineva värvusega valguslained hakkavad levima erinevais suundades.
Kuna prismale langes paralleelne kiirtekimp, siis prismast väljuvates erivärvilistes kiirtekimpudes on ka kiired paralleelsed. Aga igale värvusele vastav kimp levib erinevas suunas.
Need erivärvilised kiirtekimbud suunatakse pikksilma, millega spektrit vaadeldakse.
Mainime, et sarnase ehitusega on ka difraktsioonivõret kasutavad spektroskoobid. Neis on prisma kohal difraktsioonivõre.
Spektroskoobiga on võimalik vaadelda valgust kiirgavate ainete kiirgusspektreid. Oma olemuselt jaotuvad kiirgusspektrid kahte liiki: pidevspektrid ja joonspektrid.
Pidevspekter on selline, kus on esindatud pidev jada lainepikkuseid ja spektriks on värviline riba (J.4.24).
Joonspekter on selline, kus ei ole kõigi lainepikkustega valgusi ja spektroskoobis on näha erivärvilised jooned tumedal taustal. Neid jooni nimetatakse spektrijoonteks, kiirgusspektri korral ka kiirgusjoonteks (J.4.26). Spektrijoontel on joone või kriipsu kuju sellepärast, et nad on tegelikult spektraalriista sisendpilu kujutised. Kui sisendpiluks oleks ümmargune auk, siis näeksime spektris joonte asemel erivärvilisi ringe.
Tavaliselt esitatakse spektreid diagrammidena, kus näidatakse kiirguse intensiivsuse sõltuvust lainepikkusest või sagedusest (J.4.26 alumine osa).
Aga miks me näeme ühtedel juhtudel pidevspektreid, teistel jälle joonspektreid? Ja mida võimalik spektrite kujudest ja spektrijoonte asukohtadest välja lugeda? Et neile küsimustele vastata peame uurima, kuidas valgus tekib.
Dispersioon
Dispersiooniks nimetatakse aine absoluutse murdumisnäitaja sõltuvust valguse sagedusest või lainepikkusest. Kõigil ainetel, mis on nähtavas valguses läbipaistvad, väheneb absoluutne murdumisnäitaja lainepikkuse kasvades.
Vikerkaar
Vikerkaar tekib valguse murdumisest ja peegeldumisest vihmapiiskades. Vikerkaares on kõige kõrgemal punane värvus ja kõige madalamal violetne (lilla) värvus. Teist järku vikerkaares on värvused vastupidised, st. kõige kõrgemal on lilla vä
Spekter
Spektriks nimetatakse diagrammi, mis näitab valguse intensiivsuse jaotumist lainepikkuste või sageduste järgi.
Spektraalriist
Spektraalriist on seade spektri saamiseks, vaatlemiseks ja mõõtmiseks. Spektraalriistas kasutatakse valguse komponentideks lahutamiseks kas prismat või difraktsioonivõret. Spektrijoon on spektraalriista sisendpilu kujutis.
Oleme uurinud elektromagnetlainete, sealhulgas valguse levimist. Teame ka juba, et valguse kiirgumine seisneb selles, et aineline objekt tekitab oma energia arvel täiendava väljaportsjoni ehk kvandi. Neeldumisel annab kvant oma energia ja impulsi mingile ainelisele objektile ära ning lakkab olemast.
| J.4.28 Valguse kiirgumise vesiniku aatomis. | Simulatsioonis saab võrrelda läbi aegade vesiniku kiirgusspektri kirjeldamiseks kasutatud füüsikalisi mudeleid reaalse eksperimendiga. Ergastamiseks saab kasutada nii valget kui ka ühevärvilist valgust. Jälgida saab vesiniku elektroni liikumist energiatasemete vahel ning kiiratava valguse spektrit spektromeetris. |
Igasugust elektromagnetlainet (mitte ainult valgust!) kiirgavad ja neelavad ainelised objektid, mille mõõtmed on selle valguse lainepikkusega samas suurusjärgus. Nii on raadiolainete tekitamiseks tarvis antenne mõõtmetega mõnest millimeetrist kuni mõne meetrini. Valgust (optilist kiirgust)tekitavad aga peamiselt aatomite väliskihtide elektronid.
Juba Füüsikalise looduskäsitluse aluste kursuses saime teada, et aatomite maailmas, mida nimetatakse ka mikromaailmaks, kehtivad hoopis teised seadused, kui meile silmaga nähtavas maailmas ehk makromaailmas. Näiteks mikromaailmas on mõned füüsikalised suurused kvantiseeritud. See tähendab, et neil ei saa olla suvalisi väärtusi, vaid ainult teatud kindlaid väärtusi. Need väärtused saavad üksteisest erineda vaid kindlate suuruste – nn kvantide kaupa. Üheks selliseks suuruseks on energia. Tuleb välja, et aatomitel saab olla ainult teatud kindla väärtusega energiaid.
Energia kvantolemus võib ilmneda ka makromaailmas. On selliseid olukordi, kus kehal saavad olla ainult kindlad energia väärtused. Näiteks trepil seisval inimesel on kas ühele või teisele astmele vastav potentsiaalne energia. Kahe astme vahepealset asendit ja vastavat energiat ei õnnestu saavutada.
Aatomi energia on määratud tuuma ja elektronide vastastikmõju energiatega. Mida suuremad on elektronide energiad tuuma suhtes, seda suurem on ka aatomi energia. Elektroni energia aga on seda suurem, mida suurem on elektroni tõenäolisim kaugus tuumast. Sarnane olukord valitseb ka näiteks raskusjõu korral: mida kõrgemale maapinnast keha tõsta, seda suuremaks keha potentsiaalne energia muutub.
Kuna elektronid saavad aatomis olla tuumast vaid kindlatel kaugusel, siis see tingib ka aatomi energiate kvantiseerituse. Miks elektronide kaugused tuumast on kvantiseeritud, seda saame teada Mikro- ja megamaailma füüsika kursuses.
Elektronide lubatud energiaid kirjeldavad energiatasemed ehk energianivood.
Joonisel 4.29. on toodud ühe elektroni mõne energiataseme skeem, kus tasemeid kujutatakse horisontaalsete lõikudena. Mida kõrgemal lõik on, seda suurem energia sellisele olekule vastab. Mingile energiatasemele vastav energia väärtus on määratud ühe täisarvuga, mida kutsutakse peakvantarvuks ja selle tähiseks on .
Kõige madalam tase vastab elektroni põhiolekule (), kus elektroni tõenäoseim kaugus tuumast on minimaalne. Sellises olekus saab elektron olla kuitahes kaua. Teistelt tasemetelt püüab ta esimesel võimalusel üle minna põhiolekusse.
Kui elektron satub mingil põhjusel kõrgemale energiatasemele, siis öeldakse, et aatom on ergastatud. Sellele vastab suurem energia kui on aatomil põhiolekus.
Kuna looduses kehtib energia miinimumi printsiip, siis iga keha või süsteem püüab võimalusel minna üle olekusse, kus selle energia on minimaalne. Nii ka aatom läheb varsti pärast ergastumist tagasi põhiolekusse, st elektron läheb olekusse, kus ta peakvantarv . Aeg, mille jooksul aatom on ergastatud olekus, on keskeltläbi 10-8s.
Põhioleku energia on väiksem kui ergastatud oleku energia. Seepärast aatomi energia väheneb põhiolekusse üleminekul ja üleliigne energia kiiratakse aatomist välja elektromagnetilise lainena. Kui see laine on inimese silmale nähtav, räägitakse, et aatom kiirgab valgust.
| J.4.30 Aatomite kõrgematele energiatasemetele viimine toimub näiteks gaaslahenduslampides. Sellel pildil on näha erinevate gaasidega täidetud gaaslahenduslambid. | Erineva energiaga valguskvandid e footonid avaldavad erinevatele molekulidele erinevat mõju. Kui kõrgema energiaga footonid suudavad mõne õhus leiduva molekuli lõhkuda, siis madalama energiaga footonid ergastavad molekulide võnkeolekuid. Käesolev simulatsioon näitab mõningaid selliseid asendeid. |
Iga keemilise elemendi aatomid kiirgavad ainult sellele elemendile iseloomulikku valgust, sest ühe aine kõikidel aatomitel on ühesugune elektronide energiatasemete süsteem (J.4.30).
Aine aatomid võivad ergastuda ja hakata valgust kiirgama mitmel põhjusel. Meie käsitleme kaht kiirguse liiki: soojuskiirgust ja luminestsentsi.
Soojuskiirgus on elektromagnetiline kiirgus, kus aatomite ergastumine toimub soojusenergia arvel. Mida kõrgem on keha temperatuur, seda kiiremini selle aatomid (või molekulid) liiguvad, kas kulgevad või võnguvad. Liikumise käigus võivad aatomid omavahel põrkuda ja selle tulemusena võib mõni elektron aatomis minna tuumast kaugemale. Toimub aatomi ergastamine ja sellele järgnev elektromagnetlaine kiirgamine.
Hõõguvate tahkiste ja vedelike kiirgusspekter on pidev. Mida kõrgem on keha temperatuur, seda suurem on kiiratava valguse intensiivsus ja seda lühemalaineline on kiiratav valgus (J.4.31).
Samal temperatuuril kiirgavad tumedad kehad rohkem valgust kui heledad kehad.
Soojuskiirgus võib olla kas silmale nähtamatu infravalgus või nähtav valgus. Seda kiirgavad kõik kehad, mille temperatuur on kõrgem absoluutsest nulltemperatuurist (0 K).
Infravalgust näevad mitmed öise eluviisiga röövloomad, näiteks lõgismadu, kelle näos olevad soojusandurid lubavad tal jahti pidada ka täielikus pimeduses. On esinenud juhtumeid, kus tapetud lõgismadu on ka pärast surma salvanud inimest kätte, kui see on käe mao pea lähedale pannud. Nimelt käivitavad infrapuna sensorid lõgismaol automaatselt hammustamisrefleksi. Ja kuna roomajate refleksid hääbuvad pärast surma aeglaselt, ongi õnnetusi juhtunud.
Infravalguse toimel põhineb ka termograafia, mille abil tehakse kindlaks näiteks elamute soojuslekke kohad. Nendest kohtadest väljub ka infravalgust, mille muudavad inimesele nähtavaks termokaamerad.
Infravalguse kasutamisel põhineb ka öönägemisseadmete, kontaktivabade termomeetrite ja liikumisandurite töö.
Luminestsents on elektromagnetiline kiirgus, kus aatomite ergastamine toimub teiste energialiikide, mitte soojuse arvel. Kuna luminestsentskiirguse tekkimiseks pole vajalik kõrge temperatuur, siis on luminestsentsi nimetatud ka "külmaks valguseks". Luminestsentsi korral on aatomil mitmeid võimalusi ergastumiseks. Luminestsentsi liigitamine ergastamisviiside järgi on toodud tabelis.
|
Luminestsentsi liik |
Ergastamisenergia allikas |
|
Fotoluminestsents |
Ultravalgus |
|
Katoodluminestsents |
Kiirete elektronide juga |
|
Radioluminestsents |
Radioaktiivne kiirgus |
|
Elektroluminestsents |
Elektriväli |
|
Kemoluminestsents |
Keemiline reaktsioon |
|
Bioluminestsents |
Biokeemiline reaktsioon |
Erinevalt soojuskiirgusest ei lõpe luminestsents kohe pärast ergastamise lõppu, vaid kestab veel mingi aja, kuigi järjest nõrgenedes. Öeldakse, et luminestsentsi korral esineb järelhelendus. See võib kesta ainult mõni miljondik sekundit, aga ka mitmeid tunde. Kõik oleneb ainest, mis kiirgab.
Luminestsentsi kasutatakse näiteks päevavalguslampides ja kompaktpirnides ehk säästupirnides. Neis on lambi sisepind kaetud luminestseeriva aine ehk luminofooriga. Torus on elavhõbeda aur, millest elektrivoolu toimel kiirgub ultravalgust. See ergastab luminofoori aatomeid ja tekib luminestsentskiirgus, mis valgustab ümbrust. Sellistes lampides muudetakse valgusenergiaks kuni 80 % kulutatud elektrienergiast. Hõõglampide korral muutub valguseks kuni 15% elektrienergiast.
Luminestsentskiirgus on ka näiteks kollaste tänavalaternate valgus, kus kiirgab naatriumi aur. Ka vanemate televiisorite ja arvutite kineskoopkuvarid annavad luminestsentskiirgust, mis tekib nende sisepinnal oleva luminofoori pommitamisel kiirete elektronidega.
Luminestsents leiab kasutamist veel paljudes eluvaldkondades: ainete kristallstruktuuri ja keemilise koostise analüüsimisel, laserites, haiguste diagnoosimisel proovide põhjal, dokumentide ja rahade turvaelementides, toiduainete kvaliteedi kontrollimisel, mere naftareostuse uurimisel, süvamereloomadel vaenlaste peletamiseks või saagi ligimeelitamiseks jne.
Miks muundub luminestsentslampides palju suurem osa juurdeantavast energiast valguseks kui hõõglampides?
Soojuskiirguse korral antakse ergastav energia ainele tervikuna, st pannakse kiiremini liikuma aine aatomid. Osa sellest energiast läheb elektronide ergastamiseks. Luminestsentsi korral antakse aga ergastav energia enamasti otse elektronidele.
Teame, et mingi keha liigutamiseks on vaja anda talle kineetilist energiat, mis on võrdeline keha massiga. Kuna aatomid on palju massiivsemad elektronidest, siis on selge, et aatomite energia suurendamiseks on palju rohkem välist energiat vaja kui elektroni energia suurendamiseks.
Eelmises alajaotuses me saime teada, et iga keemilise elemendi aatomid kiirgavad ainult sellele elemendile iseloomulikku valgust. Keemiliste elementide segude või molekulide spektrid on oluliselt keerulisemad ning siis on spektrite kaudu ainete koostise ja omaduste teada saamine keerulisem ülesanne. Kui spektrid on erinevate aatomite ja molekulide jaoks erinevad, siis peaks saama neid kasutada ainete keemilise koostise analüüsimiseks. Nii ka tehakse. Vastavat uurimismeetodit nimetatakse spektraalanalüüsiks.
Kõrge temperatuurini kuumutatud tahked kehad ja vedelikud ning tihedad hõõguvad gaasid annavad pideva spektri. Pidevspekter on näiteks Päikese või hõõglambi valgusel.
Joonisel 4.31 me juba nägime, et pidevspektri kuju ja maksimumi asukoht olenevad aine temperatuurist. Mida kõrgem on temperatuur, seda rohkem valgust kiiratakse. See tähendab, et valguse intensiivsus on suurem. Pidevspektri maksimum nihkub temperatuuri tõustes lühemate lainepikkuste poole. See põhjustab ka hõõguva keha värvuse muutumist. Näiteks 700 °C kuumutatud raud hõõgub punaselt, aga temperatuuri järjest tõstes muutub kiirgus oranžikaks ja kollaseks.
Joonspektri annavad kõik gaasilised ained madalal rõhul. Joonspektri annab näiteks päevavalguslamp, mis on täidetud elavhõbeda auruga. Selle lambi spektris on tegelikult lisaks spektrijoontele ka pideva spektriga taust ehk foon.
Spektris olev kiirgusjoonte arv ja intensiivsus iseloomustab just selle aine aatomeid. See lubab aineid kiirgusspektrite järgi üksteisest eristada.
Selgub, et kõikide tahkete ainete soojuskiirguse spektrid on ühel temperatuuril täiesti sarnased pidevspektrid. Aga kuidas tekib pidev spekter? Miks nüüd iga aatom ei kiirga ainult kindlate lainepikkustega valgust?
Kiirgab küll, ainult nüüd pole aatomid isoleeritud, st pole üksteisest sõltumatud. Mida see tähendab? See tähendab, et elektronide energiatasemed ei ole igas aatomis täpselt sellised nagu üksikus, "normaalses" aatomis.. See on kursuses Füüsikalise looduskäsitluse alused õpitud tõrjutusprintsiibi üks avaldumisvorme – lähestikku paiknevad aatomid ei saa olla täpselt ühesugustel energiatasemetel. Nii võibki ergastatud aatom tahkes kehas kiirata hoopis teiste lainepikkustega valguslaineid, kui seda teeb üksik aatom ning erinevate joonspektrite summana moodustub pidevspekter.
Lisaks valguse kiirgamisele ained ka neelavad valgust. Seda, millise lainepikkusega valgust ja kui palju mingi aine neelab, kirjeldab neeldumisspekter. See võib olla nii pidev- kui joonspekter.
Neeldumisspektri saamiseks lastakse valge valgus enne spektraalriista suunamist läbi uuritava aine.
Osutub, et külm gaas neelab täpselt samade lainepikkustega valguslaineid, milliseid see kuumas olekus kiirgab. Öeldakse, et neeldumisspekter on kiirgusspektri "negatiiv". See tähendab, et neeldumisspektris asuvad neeldumisjooned samades kohtades kui kiirgusspektris on kiirgusjooned.
Analüüsimiseks ei piisa spektri vaatlemisest ja sellepärast tuleb kasutada spektromeetreid, mille abil saab mõõta erinevate spektrijoonte intensiivsust.Spektraalanalüüs on väga tundlik meetod. Selle abil saab kindlaks teha üliväikesi ainekoguseid mingi teise aine koostises. Eriti häid tulemusi molekulide "äratundmisel" annavad laserspektroskoopia meetodid, mis lubavad eristada isegi üksikuid molekule. Taoliste uuringutega tegelevad ka Tartu füüsikud.
Ainete koostise teadmine on oluline mitmetes eluvaldkondades: farmaatsia, mineraloogia, loodushoid, metallurgia, masinaehitus, kriminalistika, rääkimata astrofüüsikast, keemiast, bioloogiast.
Spektraalanalüüsil on keemilise analüüsi meetoditega võrreldes mitmeid eeliseid. Näiteks ei mõjuta spektraalanalüüs erinevalt keemilisest analüüsist ainete keemilist koostist. Samuti piisab analüüsiks väga väikestest ainekogustest. Ainete koostist saab uurida ka eemalt, ilma ainet laborisse toomata. See lubab uurida näiteks taevakehade koostist.
Spektraalanalüüsi abil on kindlaks tehtud Päikese ja tähtede keemiline koostis. Selleks võrreldakse tähtede spektreid meile tuntud keemiliste elementide spektritega (J.4.34). Siiani on tähtedel leitud ainult selliseid keemilisi elemente, mis esinevad ka Maal. See lubab arvata, et kogu universum koosneb ühesugustest keemilistest elementidest.
Kiirgumine
Kiirgumine on ainest elektromagnetlainete väljumine. Spektraalanalüüs lubab spektri põhjal kindlaks teha aine keemilise koostise.
Elektroni energiatasemed aatomis
Aatom saab olla ainult kindlate energiatega olekutes, mida kirjeldavad energiatasemed ehk energianivood. Elektroni energiatasemele vastav energia väärtus on määratud täisarvuga n = 1, 2, 3, ... Seda arvu nimetatakse peakvantarvuks.
Põhiolek, ergastatud olek, üleminekud nende kahe vahel
Olekus, kus elektron on tuumale kõige lähemas võimalikus seisundis, on n = 1 ja seda olekut nimetatakse põhiolekuks. Kui aatom saab energiat juurde, siis ta läheb mingisse suurema energiaga olekusse ja selle kohta öeldakse, et aatom ergastus. Kui aatom läh
Soojuskiirgus
Soojuskiirgus on elektromagnetiline kiirgus, mille korral aatomite ergastamine toimub soojusliikumise energia arvel.
Luminestsents
Luminestsents on elektromagnetiline kiirgus, mille korral aatomite ergastamine toimub teiste energialiikide, mitte soojuse arvel. Luminestsentsile on iseloomilik järelhelendus ehk neeldumisel salvestunud energia vabanemine kiirgusena neeldumisprotsessi kestusest oluliselt pikema aja jooksul.
Alustuseks on ehk paslik mainida, et ei ole hea mõte saada päriselt nähtamatuks, nagu mõnes raamatus või filmis seda kujutatud on. Miks? Lihtne – kui keegi on nähtamatu, siis on nähtamatud ka tema silmad, st tema silmaläätsed ei murra valgust ning tema võrkkest ei neela valgust. Järeldus on ilmne – nähtamat inimene on ühtlasi pime. See arvatavasti nullib kõik eelised, mis nähtamatuks olemine muidu anda võiks.
Vaadake joonist 4.35 ning proovige vastata küsimusele, mida näeb vaatleja, kui ta vaatab suunaga vasakult paremale punase valgusallika poole? Õige vastus on, et sedasama üksikut valgusallikat. Sest silm ei saa kuidagi aru, kas valguskiir on vahepeal mõne käänu sisse teinud, kui tema lõpp-suund teekonna lõpus on samasugune, kui alguses - kui suund on sama, siis koonduvad nad ikkagi punktiks, mis on valgusallika kujutiseks silma võrkkestal. Kui tõdeme, et igasugust objekti võib vaadelda kui punktvalgusallikate kogumit ja kui sfääriline objekt käitub niimoodi suvalisest suunast temale langevate valguskiirtega, siis ongi küsimus „kuidas saada nähtamatuks“ põhimõtteliselt vastatud – suur sfääriline objekt silma ja valgusallika vahel on nähtamatu.
Aga panna valguskiirt sellist käänakut tegema? Jah, see on keeruline koht. Sest valguskiired ei muuda niisama heast peast oma suunda. Ning te võite kontrollida - optiliselt hõredamast keskkonnast (õhk) optiliselt tihedamasse keskkonda (sfäär) liikudes murduvad nad “teistpidi”.
Edasises arutluses peaksime eristama kahte olukorda. Ühel juhul asetseb vaatleja objektist nii kaugel, et nägemise stereoefekt ning võimalikud erinevated rakursid (liigutad pead ühele ja teisel poole) ei mängi erilist rolli. Teisel juhul on objekt vaatlejale lähedal.
Kaugel asetseva objekti “nähtamatuks” tegemiseks võime objekti ette paigutada seda varjava ekraani, millele kuvatakse pilt, mis on vaatlejat poolt vaadates objekti taga (J.4.36). Nii et objekti poole vaadates näeme seda, mis on objekti taga (ja mis tegelikult ongi ju nähtamatuse definitsioon). Aga vaatleja peab siis olema ühes kindlas punktis ning kui objekt liigub, siis peab muutuma ka ekraani asukoht ja pilt sellel … põhimõtteliselt on see nagu suure pildi taha varjumine.
Nähtamatuks tegeva sfäärilise kookoni valmistamiseks (J.4.35) peaksime kasutama eriliste omadustega materjale – metamaterjale - mis on parajasti “kuum teema” teadusajakirjanduses. Selgub nimelt, et metamaterjalide murdumisnäitaja on negatiivne ning joonisel J.4.35 kujutatud olukord on põhimõtteliselt võimalik.
| Eksperimentaalselt demonstreeriti nähtamatuks tegeva mantli võimalikkust esmakordselt 2006.aastal Duke’i Ülikoolis. Kui vasakul pildil liigub keralaine vabalt, siis paremal pildil on tema teele asetatud silindriline takistus. Näeme, et pärast sellist takistust moodustuvad uuesti keralaine lainefrondid. Eksperiment on tehtud infravalgusega. | J.4.37 Sellised näevad välja metamaterjalid. |
Miks on negatiivne murdumisnäitaja eriline nähtus?
Aga eranditult kõigi “normaalsete” materjalide murdumisnäitaja on positiivne. Ja metamaterjalid ei ole materjalid selle sõna tavalises mõistes, pigem on tegemist ülitiheda kärgstruktuuriga (J.4.37). Ja tõelise nähtamatuks tegeva mantlini on teadlastel veel väga pikk tee minna.
Niisiis, sellel pildil on nähtamatu kass. Ja tema silmadega on kõik korras. Aga kas kass hiirt näeb?