Füüsika 8.klassile
- Füüsika 8. klassile
- 1 Optika
- 1.1 Valgus. ValgusallikadLisamaterjalidLisaülesanded
- 1.2 Valgus kui energiaLisamaterjalidLisaülesanded
- 1.3 Päike, tähtLisamaterjalidLisaülesanded
- 1.4 Nähtav valgus kui liitvalgusLisamaterjalidLisaülesanded
- 1.5 ValgusfilterLisamaterjalidLisaülesanded
- 1.6 Valguse sirgjooneline levimineLisamaterjalidLisaülesanded
- 1.7 Valguse kiirusLisamaterjalidLisaülesanded
- 1.8 Vari. Varjutused. Kuu faasidLisamaterjalidLisaülesanded
- 1.9 Peegeldumine. PeegeldumisseadusLisamaterjalidLisaülesanded
- 1.10 Esemete nägemine. Värviline pindLisamaterjalidLisaülesanded
- 1.11 Tasapeegel, eseme ja kujutise sümmeetrilisusLisamaterjalidLisaülesanded
- 1.12 Kumer- ja nõguspeegelLisamaterjalidLisaülesanded
- 1.13 Valguse murdumineLisamaterjalidLisaülesanded
- 1.14 Esemete näiv ja tegelik asukohtLisamaterjalidLisaülesanded
- 1.15 Valguse täielik peegeldumineLisamaterjalidLisaülesanded
- 1.16 Kumerlääts. NõgusläätsLisamaterjalidLisaülesanded
- 1.17 Kujutised. LuupLisamaterjalidLisaülesanded
- 1.18 Kujutise konstrueerimineLisamaterjalidLisaülesanded
- 1.19 Silmad. Prillid. Lühi- ja kaugnägelikkusLisamaterjalidLisaülesanded
- 1.20 Fotoaparaat. MikroskoopLisamaterjalidLisaülesanded
- 1.21 TeleskoopLisamaterjalidLisaülesanded
- 1.22 Google’i prillid ja liitreaalsusLisamaterjalidLisaülesanded
- 2 Mehaanika
- 2.1 Mehaaniline liikumineLisamaterjalidLisaülesanded
- 2.2 Liikumise kujutamine graafikulLisamaterjalidLisaülesanded
- 2.3 Mass kui keha inertsuse mõõtLisamaterjalidLisaülesanded
- 2.4 Kehade vastastikmõjuLisamaterjalidLisaülesanded
- 2.5 GravitatsioonLisamaterjalidLisaülesanded
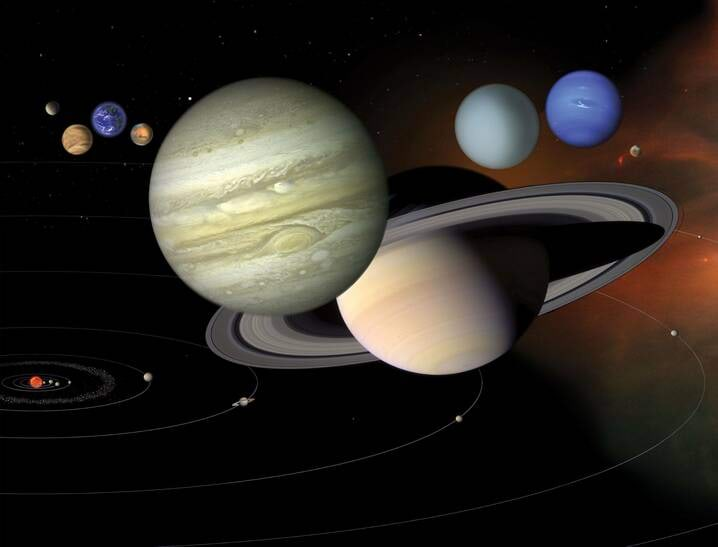
- 2.6 PäikesesüsteemLisamaterjalidLisaülesanded
- 2.7 Hõõrdumine. HõõrdejõudLisamaterjalidLisaülesanded
- 2.8 Deformeerimine, elastsusjõudLisamaterjalidLisaülesanded
- 2.9 RõhkLisamaterjalidLisaülesanded
- 2.10 Pascali seadusLisamaterjalidLisaülesanded
- 2.11 Aine tihedusLisamaterjalidLisaülesanded
- 2.12 Rõhk vedelikes erinevatel sügavustelLisamaterjalidLisaülesanded
- 2.13 ManomeeterLisamaterjalidLisaülesanded
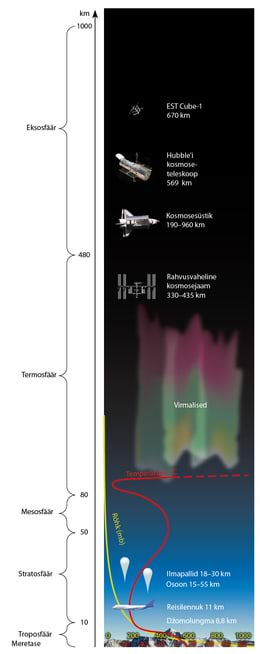
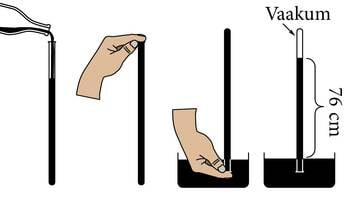
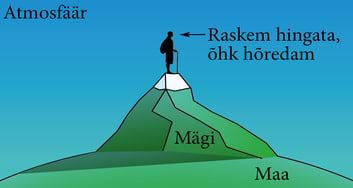
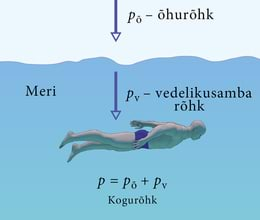
- 2.14 Maa atmosfäär. ÕhurõhkLisamaterjalidLisaülesanded
- 2.15 ÜleslükkejõudLisamaterjalidKordamine ja kontrolltööLisaülesanded
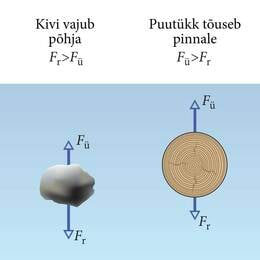
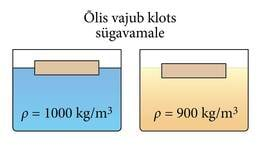
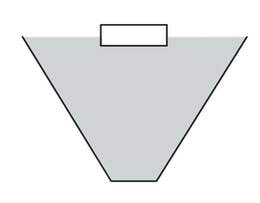
- 2.16 Keha ujumine, ujumise ja uppumise tingimusLisamaterjalidLisaülesanded
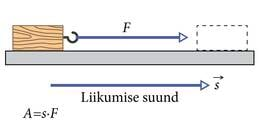
- 2.17 Mehaaniline töö ja energiaLisamaterjalidLisaülesanded
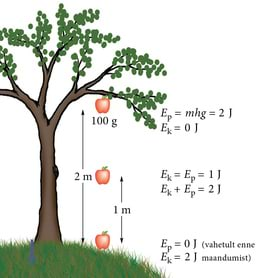
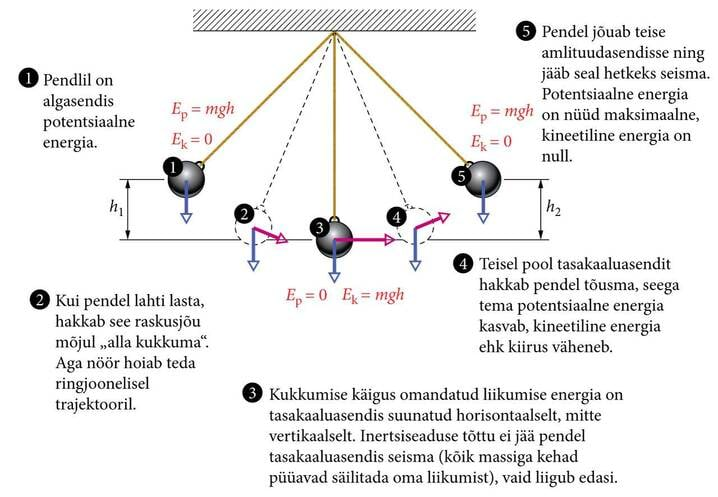
- 2.18 Kineetiline ja potentsiaalne energiaLisamaterjalidLisaülesanded
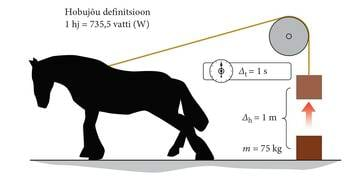
- 2.19 VõimsusLisamaterjalidLisaülesanded
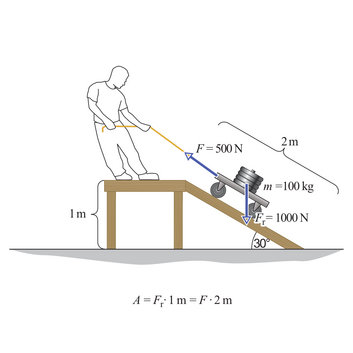
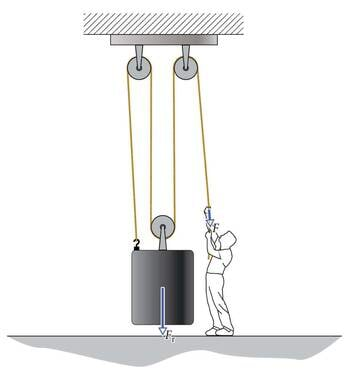
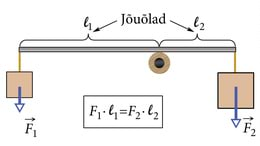
- 2.20 Lihtmehhanismid. KasutegurLisamaterjalidLisaülesanded
- 2.21 Lihtmehhanismidest täpsemalt, koos arvutustegaLisamaterjalidLisaülesanded
- 2.22 VõnkumineLisamaterjalidLisaülesanded
- 2.23 Heli tekkimine ja levimineLisamaterjalidLisaülesanded
- 2.24 Heli kõrgus ja heli valjusLisamaterjalidLisaülesanded
- 2.25 Müra ja mürakaitseLisamaterjalidLisaülesanded
Autor Erkki Tempel
Retsensendid Jaan Paaver, Henn Voolaid
Toimetaja Kaido Reivelt
Keeletoimetaja Piret Põldver
Joonised Nils Austa, Heiko Unt
Kassipildid joonistas Urmas Nemvalts
Täname
TÜ Füüsika Instituut, TÜ Koolifüüsika Keskus, Taavi Tuvikene, Tõnis Eenmäe, Peeter Tenjes, Mari Reilson, Maret Lepplaan, Kristel Uiboupin, Rünno Lõhmus, TÜ Arvutiteaduse Instituut, Tartu Tähetorn, Jaak Kikas ja Materjalimaailm.
08.07.2022 K.Reivelt
- Vahetatud on mehaanikas alajaotuste Inertsus ja Aine tihedus paigutus õpikus. Õpik algab nüüd alajaotusega Mehaaniline liikumine, mis on sisuliselt loogilisem.
- Vahetatud on tähised. Võimsust tähistame nüüd tähega .
- Vahetatud on Päikese siseehitust ja välisstruktuuri kirjeldav joonis.
- Sisse on viidud hulk keelekorrektuuris välja tulnud vigu ja ebatäpsusi.
Ka tekstisisesed valemid tuleks viia latex formaati.
Alati, kui me midagi näeme, ümbritseb meid valgus. Valguse kaudu saame enamuse infost meid ümbritseva maailma kohta. Ilma valgusenergiata oleks elu Maal võimatu. Aga mis on valgus?
Valguse võib laias laastus jagada kaheks: nähtavaks valguseks ja nähtamatuks valguseks. Seda valguse osa, mida me näeme, nimetatakse nähtavaks valguseks. Nähtamatu valgus on aga ultraviolettvalgus ja infrapunavalgus. Nii võib öelda, et valgus ümbritseb meid isegi siis, kui viibime täiesti pimedas ruumis.
Infrapunavalgus ehk infravalgus ehk soojuskiirgus ümbritseb meid ka täiesti pimedas ruumis, kuna kõik soojad kehad kiirgavad infravalgust. Lisaks infravalgusele ümbritseb meid veel ultraviolettvalgus ehk ultravalgus (ka UV-kiirgus), mida me ei näe, kuid mis meid mõjutab – näiteks me päevitume ultravalguse toimel.
Kehasid, mis kiirgavad valgust, nimetatakse valgusallikateks. Mõned valgusallikad kiirgavad lisaks valgusele ka soojust, selliseid valgusallikaid nimetatakse soojuslikeks valgusallikateks.
Soojuslikes valgusallikates tekib valgus osakeste soojusliikumisel. Soojuslikud valgusallikad on näiteks Päike ja lõke. Hõõglamp on samuti soojuslik valgusallikas, kuna selles tekib valgus hõõgumiseni kuumutatud hõõgniidist (traadist), mille temperatuur võib ulatuda üle 3000 ˚C.
Lisaks soojuslikele valgusallikatele on olemas ka külmad valgusallikad. Sellised valgusallikad kiirgavad valgust, kuid soojust väga vähe. Ka selliste valgusallikatega puutume kõik igapäevaselt kokku – näiteks telefoni- ja arvutiekraaniga. Külmi valgusallikaid kohtame ka looduses, näiteks suvel pimedas metsas võib märgata rohekaid helendavaid „tulukesi”, emaseid jaanimardikaid, kes oma tuledega annavad märku isastele jaanimardikatele. Polaaraladel võib mõnikord taevas märgata virmalisi, mis on samuti külmad valgusallikad. Virmalised erinevad teistest valgusallikatest selle poolest, et neid ei saa kätte võtta ja vaadelda kui kehasid.
Tänapäeval on laialdaselt kasutusel valgusdioodid (rahvusvaheline lühend LED), mida kasutatakse näiteks arvuti-, nutitelefonide ja telerite ekraanides. Kuna LED-valgustid on väga energiasäästlikud, kasutatakse neid ka tavaliste hõõg- ja säästulampide asemel.
Kõik valgusallikad vajavad valguse tekitamiseks energiat. Valgusallikad saavad oma energia keemilise reaktsiooni energiast (lõke, küünlaleek, jaanimardikad), tuumareaktsioonidest (Päike, teised tähed) või elektrienergiast (hõõglambid, arvuti- ja telefoniekraanid).
Valguse kätte jäetud esemed soojenevad. Pikaks ajaks päikese kätte jäetud esemed pleekuvad. Päikesepatareisid kasutatakse elektrienergia saamiseks. Millise energia arvel need protsessid toimuvad?
Valgusel on energia. Kui valguse energia neeldub, siis kehad soojenevad. Pleekimisel valguse energia toimel värvi molekulid lagunevad ning värvus muutub. Nägemine põhineb samuti keemilisel reaktsioonil – valgus tekitab silma valgustundlikes rakkudes keemilisi reaktsioone. Valguse energia arvel toimub ka fotosüntees.
Ultravalguse footonitel on suurem energia ning nii võib ultravalgus inimesele ohtlik olla. Ultravalguse toimel inimesed päevituvad – nahk muutub pruuniks. Viibides aga päikese käes pikka aega, võib tekkida punetus ning nahapõletik – see on tingitud liigsest ultravalgusest, mis on nahas vallandunud fotokeemilise reaktsiooni tagajärg. Liigne ultravalgus võib lisaks naha punetusele tekitada ka nahavähki ning mikroorganismidele mõjub ultravalgus surmavalt.
Maad kaitseb liigse ultravalguse eest atmosfääri ülemistes kihtides paiknev osoonikiht (O3). Erinevates Maa piirkondades on ultravalguse tase väga erinev, kuna osoonikihi paksus ei ole igal pool sama. Kohti, kus osoonikiht on hõrenenud, nimetatakse osooniaukudeks. Nendes piirkondades jõuab maapinnale ohtlikus koguses ultravalgust.
Infravalgust kiirgavad kõik soojad kehad, sellepärast võib seda nimetada ka soojuskiirguseks – me tajume seda soojusena, kui satume lõkke või kuuma pliidi lähedale. Kõrgema temperatuuriga kehade soojuskiirgus on tugevam, külmade kehade soojuskiirgust me füüsiliselt ei taju. Väga intensiivne soojuskiirgus võib põhjustada ka põletust, süüdata või sulatada esemeid.
Tähtis on meeles pidada ka seda, et ilma valguse energiata oleks Maa lihtsalt üks külm kivitükk. Kõik, mis me igapäevaselt enda ümber elamas ja liikumas näeme, saab oma energia kas otsesel või kaudsel viisil Päikeselt ja valdavalt just valguse energiana, olgu selleks siis tuul, vihmapilvede tekkimine, taimede kasvamine või organismide arenemine.
| Selle lennuki nimi on Solar Impulse ning see on esimene päikeseenergial töötav lennuk, mis lendas ümber maailma. Päikeseenergia kogumiseks on kõik tema tiivad ja kere pealtpoolt kaetud päikesepatareidega. Oma teekonna lõpetas ta 2016. a. | Taifuun vaadatuna maalähedaselt orbiidilt rahvusvahelise kosmosejaama (ISS) pardalt. Ka taifuunid saavad oma energia Päikeselt. |
Kuigi Päike soojendab korraga vaid Maa ühte külge, ei kõigu Maal ööpäevane temperatuur väga palju – Maad ümbritseb atmosfäär, mis ei lase Maal soojuskiirgusena liiga palju energiat kaotada. Näiteks meie naaberplaneedil Marsil, kus atmosfäär on väga hõre, muutub temperatuur ööpäeva jooksul väga palju – päevane temperatuur võib tõusta kuni 25 ˚C-ni ning öine langeda –125 ˚C peale.
Päike on üks enam kui 100 miljardist tähest Linnutee galaktikas. Päikesel muutub vesinik termotuumareaktsioonis heeliumiks. Selle protsessi käigus eraldub tohutult energiat – igas sekundis 3,6x1026 J, see on miljoneid kordi rohkem kui tarbitakse kogu maailmas terve aasta jooksul. Päike on oma praegusel kujul eksisteerinud juba 5 miljardit aastat ning astrofüüsikute hinnangul kiirgab Päike samamoodi energiat veel umbes 5 miljardit aastat.
Maale jõuab ainult väga väike osa Päikese energiast (umbes 1 miljardik kogu Päikese kiiratud energiast). Kuid see energiakogus on täiesti piisav, et Maal saaks eksisteerida elu.
Galaktika on tohutu tähelise ja tähtedevahelise aine kogum, mida hoiab koos tema enda gravitatsioon. Seda galaktikat, kus meie elame, nimetatakse tihti erinimega Linnutee. Päike asub Galaktika osas, mida nimetatakse Galaktika kettaks – suur ringikujuline lapik piirkond, mis sisaldab enamuse Galaktika heledatest tähtedest ja tähtedevahelisest ainest. Kuna me oleme ketta sees, siis paistab Galaktika ketas öise tumeda taeva taustal heleda ribana ning sellest tulenebki nimetus Linnutee. Vaadates ketta tasandiga ristisuunas, satub vaatejoonele suhteliselt vähem tähti, samal ajal kui ketta tasandis vaadates satub vaatejoonele oluliselt rohkem tähti.
Päikesel esinevad päikesepursked, mille käigus paiskub selle pinnalt välja suures koguses ainet, mille osakesed liiguvad kiiresti läbi Päikesüsteemi. Maale jõudes hävitaksid need siinse elu üsna kiiresti. Maad kaitseb nende osakeste eest Maa magnetväli ja atmosfäär. Aeg-ajalt kuuleme Maad tabanud magnettormidest või näeme virmalisi – neid põhjustab just selline Päikese aktiivsus.
| Päikeselt purskunud laetud osakeste voog Päikeselt Maale. Maad kaitseb magnetväli, mis kallutab laetud osakesed kõrvale. Maa ümber on kujutatud Maa magnetosfääri. Sellest hoolimata jõuab osa laetud osakestest Maa magnetpooluste kaudu atmosfääri ja sellest tekivad virmalised. | Päikeselt purskunud laetud osakeste vood põhjustavad Maa atmosfääri jõudes virmalisi. |
Satelliitide ja kosmoseaparaatide jaoks on Päike ühtaegu õnn ja õnnetus. Õnn sellepärast, et päikese energia võimaldab toota elektrienergiat ja satelliitide süsteeme töös hoida. Samas kahjustab intensiivne ultravalgus (aga eriti röntgen- ja gammakiirgus ning kosmiline kiirgus) pidevalt satelliidi süsteeme.
Vahel vihmase ilmaga me näeme vikerkaart. Selles on eristatavad punane, oranž, kollane, roheline, sinine, tumesinine ja lilla värvus. Kuna üleminek ühelt värvilt teisele toimub sujuvalt, siis võib seal hea tahtmise korral näha veel palju rohkem värve. Kust need värvid tulevad?
Füüsikud ütlevad selliste nähtuste põhjal, et valge valgus on liitvalgus, st ta koosneb erinevat värvi valgustest. Tõepoolest, kuna vesi vihmapiiskades ise valgust ei kiirga, peab kogu see värvikirevus tulema Päikese valguse „seest“, vihmapiisad teevad need värvid lihtsalt nähtavaks. Tekkivat värvide paletti nimetatakse spektriks.
Valguse spektri mõiste võttis kasutusele Isaac Newton juba 1666. aastal. Newton sai spektri nii, et lasi läbi klaasprisma kitsa valgusvihu, katse tulemusena tekkis ekraanile värviline riba.
Newton oletas, et spektri värviliste valguste liitmisel saadakse uuesti valge värvus. Tal oli õigus ning ta tõestas seda ka katseliselt. Newton suunas spektri värvid ühte punkti ning sai tulemuseks valge valguse.
Igapäevaelus kasutame erinevaid valgusallikaid. Erinevatel valgusallikatel on üldiselt ka erinevad spektrid. Näiteks hõõglambi valgus on enamasti natuke kollakam kui päikesevalgus, kuna sisaldab vähem sinist ja violetset valgust. Valguse spektreid esitatakse tihti graafikutel, kus horisontaalsel teljel on erinevad värvid, vertikaalsel teljel see, kui tugev üks või teine värv uuritavas valguses on. Siit leheküljelt leiad küünla, LED-lambi, päevavalguslambi ja laseri spektrid nii fotol kui ka graafikul. Võrdle neid!
Valge valgus on liitvalgus, st selle spektris on olemas kõiki värvi valgused alates punasest ja lõpetades violetsega. Mida peaksime tegema siis, kui soovime liitvalgusest eraldada vaid ühte värvi valgust?
Kui suuname valge valguse läbi punase klaasi, siis tekib seinale punane valguslaik. See on sellepärast, et punasest klaasist pääseb läbi vaid punane valgus, teist värvi valgused neelduvad. Sarnaselt laseb sinine klaas läbi vaid sinist valgust, roheline klaas ainult rohelist valgust jne. Füüsikud ütlevad selle kohta valguse filtreerimine ja eri värvi klaasid on valgusfiltrid.
Valgusfiltreid saab kasutada olulise info esiletoomiseks.
Aga mida teeb näiteks roosa klaas? Sellest aru saamiseks tuleb esmalt mõista, et enamik meid ümbritsevaid valguseid on liitvalgused, sisaldades erinevat värvi valguseid, nii ka roosa valgus. Järelikult peab roosa klaas läbi laskma erinevat värvi valguseid parajasti nii, et kokku moodustuks roosat värvi valguse spekter. Ehkki tänapäeval saadakse värvilist valgust põhiliselt juba loomu poolest ühevärvilist valgust kiirgavatest valgusdioodidest, on valgusfiltritel endiselt palju rakendusi.
| Valgusfiltrid ei pea alati olema klaasist. Päevituskreemi ülesanne on blokeerida osaliselt ultrakiirgust, nii et tegelikult on ka päevituskreem valgusfilter. | Infrapunakaamerate objektiivide ette pannakse valgusfilter, mis laseb läbi ainult infravalgust. See on hea, sest nähtav valgus neid kaameraid ainult segaks. Silmaga vaadates tunduvad sellised filtrid täiesti läbipaistmatud. |
Kuna digikaamerad „näevad“ ka neid spektri piirkondi, mis on inimsilmale nähtamatud (näiteks ultraviolettvalgus ja infrapunavalgus), siis tuleb näiteks kosmosest või Päikesest tehtud ilusate värviliste piltide korral alati küsida, kas need paistavad samasugused ka inimsilmale. Inimsilmale muidu nähtamatu valgus kantakse tihti digitaalselt („photoshopitakse”) üle nähtavasse piirkonda, st iga nähtamatu valguse värv seatakse vastavusse mõne nähtava värviga.
Põnev on see, et erinevad valgusfiltrid toovad esile infot Päikese erinevate kihtide kohta. Näiteks nähtavas valguses pildistamine annab infot fotosfääri kohta, samas H-alfa filter kromosfääri kohta.
Me oleme õppinud, et valgus jõuab Päikeselt Maale. Klassiruum muutub valgeks, kui tuled põlema panna. Nende nähtuste kohta ütleme, et valgus levib Päikeselt Maale ja lampidest klassiruumi. Kuidas valgus levib?
Eespool mainisime, et valgust võib vaadelda kui energiat. Valguse levimise all mõeldaksegi valgusenergia edasikandumist ühest kohast teise.
Valguse levimiseks on vaja läbipaistvat keskkonda. Nii levib valgus gaasilistes keskkondades, aga ka läbipaistvates vedelikes ja tahketes ainetes, näiteks vees ja klaasis. Valgus võib levida ka vaakumis, kus aineosakesed puuduvad. Näiteks jõuab Maale valgus isegi teistest galaktikatest.
Keskkondi, kus valgus saab levida, nimetame optilisteks keskkondadeks. Kui valgus tungib läbi väikese augu, tekib ruumi valguskiir, mis levib otse ilma kõrvale kaldumata. Sellist valguskiirt saab tekitada ka laserpointeriga. Sellest ja teistest analoogilistest katsetest järeldame, et valgus levib sirgjooneliselt.
Joonistel kasutatakse valguse levimise kujutamiseks sirglõike, millele on kantud valguse levimise suunda tähistav nool, ja neid nimetatakse valguskiirteks.
Füüsikas on valguskiir kokkuleppeline teoreetiline mõiste, mille abil on valguse levimist lihtne kujutada ja seletada. Reaalses elus ei ole võimalik ühte valguskiirt tekitada isegi laseri abil, kõik valgusallikad tekitavad kiirtekimbu, mida nimetatakse ka valgusvihuks.
Valgusvihk on see piirkond ruumis, kus valgus levib. Valgusvihk on justkui valguskiirte kimp, kus üksikud kiired võivad, aga ei pea olema üksteisega paralleelsed. Joonistel näidatakse ära mõned iseloomulikud valgusvihu valguskiired ning valguse levimise suund.
Kui näiteks laser tekitab peaaegu paralleelse valgusvihu, siis küünal valgustab ruumi kõikides suundades.
Kõige olulisemad valgusvihkude alaliigid on hajuv, paralleelne ja koonduv valgusvihk.
Hajuva valgusvihu moodustavad kiired, mis lähtuvad ühest punktist, kuid edasi eemalduvad üksteisest – näiteks küünlavalgust võib vaadelda hajuva valgusvihuna.
Paralleelse valgusvihu korral on kõik valguskiired paralleelsed.
Koonduv valgusvihk koosneb valguskiirtest, mis üksteisele lähenevad (ideaalsel juhul koonduvad ühte punkti) – koonduv valgusvihk tekib näiteks luubi taga, kui sellele langeb päikesevalgus.
Joonistelt on selgesti näha, et paralleelne valgusvihk on ainuke, mille läbimõõt levides ei muutu. Selliseid valgusvihke saab tekitada laseri abil ja see on üks neid omadusi, mis teeb laserist nii erilise valgusallika – me võime panna elektripirni või mõne muu tavalise valgusallika külge ükskõik kui keerulise optilise süsteemi, sarnast tulemust, kui seda pakub laser, saavutada ei ole võimalik.
Looduslikuks paralleelse valgusvihu allikaks on Päike. See ei tähenda, et Päike kiirgab valgust vaid ühes suunas. Aga vahemaa Päikese ja Maa vahel on sedavõrd suur, et meieni jõudvad kiired on praktiliselt paralleelsed. Sellest arusaamiseks proovi joonistada kiiri Päikeselt Maale. Märkad, et Maani jõuavad vaid need, mis liiguvad otse Maa poole.
Veel mõnisada aastat tagasi arvati, et valgus levib ühest kohast teise hetkeliselt. Selline mulje jääb kergesti, sest näiteks süüdates toas tuled, on kogu ruum hetkega valgustatud. Tegelikult kulub ka valgusel aega, et levida ühest kohast teise. Aga kui kaua?
Üks esimesi teadlasi, kes valguse kiiruse kindlaks määras, oli Taani astronoom Ole Christensen Rømer. 1676. aastal sai ta valguse kiiruseks 220 000 km/s. Rømer määras valguse kiiruse astronoomiliste vaatluste põhjal. Alles paarsada aastat hiljem suudeti valguse kiirus täpsemalt määrata maapealsetes tingimustes.
Tänapäeval on valguse kiirus vaakumis väga täpselt teada, see on 299 792 458 m/s ehk ligikaudu 300 000 km/s.
See on väga suur kiirus – valgusel kulub Päikese ja Maa vahel laiuva ligikaudu 150 000 000 km läbimiseks ainult 8 minutit ja 20 sekundit.
Ülesanne Eesti füüsikaolümpiaadilt:
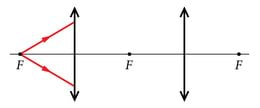
Esimese hinnangu valguse kiirusele andis Rømer 1675. a., uurides Jupiteri kaaslase Io liikumist. Io orbiit asetseb ligikaudu Maa orbiidi tasapinnas, nii et kaaslane kaob periooditi Jupiteri varju. Mõõtmised näitavad, et intervall kahe järjestikuse hetke vahel, kui Io ilmub nähtavale Jupiteri varjust, kõigub maksimaalselt ulatuses teatava keskväärtuse () ümber sõltuvalt Päikese, Maa ja Jupiteri vastastikusest asendist (vt. joonis). Teades, et Maa kaugus Päikesest on 1,5⋅108km, hinda valguse kiirust. Eeldada, et Jupiteri orbitaalkiirus ümber Päikese on palju väiksem kui Maal.
Lahendus
Io tiirlemisperioodi jooksul muutub Maa ja Jupiteri vahekaugus. Kaugus muutub kõige kiiremini, kui Maad ja Jupiteri ühendav sirge on Maa orbiidile puutujaks. Aja jooksul, mis Iol kulub ühe tiiru tegemiseks, muutub Maa ja Jupiteri vahekaugus
võrra. Selle täiendava vahemaa läbib valgus 15s jooksul, seega valguse kiirus avaldub:
Valgus levib erinevates optilistes keskkondades erineva kiirusega.
Näiteks klaasis levib valgus umbes 1,5 korda aeglasemalt kui õhus ning teemandis on valguse kiirus umbes 2,4 korda väiksem kui õhus. Õhk aeglustab valguse levimise kiirust väga vähesel määral, mistõttu võime valguse levimise kiiruseks õhus lugeda valguse kiirust vaakumis (vt tabelit).
Põhjust, miks valgus levib erinevates optilistes keskkondades aeglasemalt kui vaakumis, võib võrrelda inimese liikumisega maal ja vees – märksa lihtsam on joosta mööda maad kui rinnuni vees. Sama on ka valgusega – kuitahes läbipaistev optiline keskkond ikkagi takistab valguse levimist, mistõttu levib valgus seal aeglasemalt. Sellist nähtust iseloomustavat füüsikalist suurust nimetatakse optiliseks tiheduseks.
Astronoomias kasutatakse valguse kiirust objektidevaheliste kauguste mõõtmiseks. Valgusaasta on vahemaa, mille valgus läbib ühe aasta jooksul. Üks valgusaasta võrdub ligikaudu 9,46x1012 km-ga. Kuigi valgusaasta on väga suur pikkusühik, on universumis taevakehade vahelised kaugused isegi valgusaastates mõõdetuna väga suured. Näiteks Põhjanael asub meist 500 valgusaasta kaugusel (umbes 4,73x1015 km). Teised galaktikad asuvad meist miljonite ja miljardite valgusaastate kaugusel.
Valguse kiirus on kõige suurem kiirus, mida ükskõik milline keha võib saavutada. Nii et ka parima tahtmise juures ei jõua ükski kosmoselaev lähima täheni kiiremini, kui 4,2 aastaga. Kiiremini ei jõua meieni ka tähtedelt kiiratav valgus. Nii näemegi Põhjanaela sellisena, nagu see oli 500 aastat tagasi.
| Meie galaktikas on miljardeid tähti, mis asuvad meist 4,2 kuni 900 000 valgusaasta kaugusel. Neid vaadeldes saame infot vaid nende kauge mineviku kohta. | Juba Päikesesüsteemi ühest otsast teise lendamine mehitamata kosmoselaevadel võtab aastaid ja aastakümneid. Teoreetiliselt on siiski võimalikud n-ö hüpped läbi aegruumi ussiaukude. Pildil on kaader 2014. a filmist „Interstellar" (Tähtedevaheline), kus kosmoselaev hakkab sooritama just sellist hüpet. |
Tänapäeval on valguse kiirus ja selle täpne väärtus olulised ka maapealsetele tehnoloogiatele. Näiteks GPS-seadmed registreerivad aegasid, millal satelliitidelt saadetud signaalid nendeni jõuavad, ning arvutavad selle põhjal oma asukoha.
Valguse kiirus
Valguse kiirus on väga suur, aga siiski lõplik: vaakumis levib valgus ligikaudu 300000km/s. Teistes optilistes keskkondades levib valgus aeglasemalt, näiteks teemantis on valguse kiirus korda väiksem.
Vahemaad, mille valgus levib ühe aasta jooksul, nimetatakse valgusaastaks.
Kindlasti oled märganud päikeselise ilmaga oma varju maapinnal või käe varju seinal. Mõnikord on varjul väga teravad piirjooned, mõnikord on selle piirid aga üsna hägused. Kuidas nii?
Oleme juba rääkinud, et valgus levib sirgjooneliselt. Seega kui valguse teele panna ette mingi valgust mitte läbilaskev ese, siis valgus eseme taha ei levi. Ruumipiirkonda, kuhu valgus ei levi või levib osaliselt, nimetatakse varjuks.
Eseme taha tekkivat varju võib tinglikult jagada täisvarju ja poolvarju piirkonnaks.
Täisvari on selline ruumipiirkond, kuhu valgusallika valgus ei levi. Poolvari on ruumipiirkond, kus osa valgusallikast jääb eseme serva taha, osa veel paistab, seega on ka valgus seal nõrgem kui täielikult valgustatud alal.
Poolvari on seda laiem, mida suurem on valgusallikas ja mida lähemal see asub. Näiteks Päikese poolvari on üsna kitsas, kuna Päike asub väga kaugel. LED-lampide (valgusdioodlampide) valgusest tekkivad poolvarjud on väga kitsad, kuna nende sees olevad valgusdioodid on väga väikeste mõõtmetega. Kui klassis on terve lagi kaetud suurte valgusallikatega, siis täisvarju praktiliselt ei tekigi ja see on loomulikult hea – varju piirkonnas on halb lugeda.
Kindlasti oled kuulnud päikesevarjutusest ja kuuvarjutusest.
Päikesevarjutus tekib siis, kui Kuu jääb Maa ja Päikese vahele ning Maale langeb Kuu vari. Täisvari tekib ainult väga väikeses piirkonnas, kuid suuremal territooriumil saab jälgida osalist päikesevarjutust – Kuu varjab Päikese osaliselt. Täielikku päikesevarjutust saab jälgida ainult mõni minut.
Täielik päikesevarjutus esineb harva ning väga väikesel maa-alal. Eestis oli viimane peaaegu täielik päikesevarjutus nähtav 1961. aastal, kui Päikesest oli varjatud 88%. Järgmine täielik päikesevarjutus leiab Eestis aset 2126. aastal.
Kuuvarjutus tekib siis, kui Kuu jääb Maa varju. Teatavasti on Kuud näha seetõttu, et temalt peegeldub meile päikesevalgus, mistõttu näeme teda heledana. Kui Kuu jääb Maa varju (Päike Kuud otseselt ei valgusta), siis me Kuud heleda kettana taevas ei näe, vaid ta paistab punasena. Kuuvarjutust on võimalik jälgida suuremalt territooriumilt (umbes poolelt maakeralt) ning kuuvarjutus võib kesta tunde. Täielikku kuuvarjutust saab igas Maa kohas vaadelda keskmiselt iga 2,5 aasta järel.
See, kui suurt osa Kuust me valgustatuna näeme, sõltub Kuu, Päikese ja Maa omavahelisest paiknemisest ning erinevaid selliseid paiknemisi nimetatakse kuu faasideks. Kuu faasid muutuvad tsükliliselt – kuu loomine, noorkuu, täiskuu ja vanakuu, kuu läbib kõik faasid 29,5 ööpäevaga ja alustab siis jälle otsast peale.
Vari. Täisvari ja poolvari
Ruumipiirkonda, kuhu valgus ei levi või levib osaliselt, nimetatakse varjuks. Täisvari on selline ruumipiirkond, kuhu valgusallika valgus ei levi. Poolvari on ruumipiirkond, kus osa valgusallikast jääb eseme serva taha, osa veel paistab, seega on ka valgus seal nõrgem kui täielikult valgustatud alal.
Vaadates tuulevaikse ilmaga järve pinda, võib vee peal näha ümbritsevat loodust: puid, taevast ja päikest. Me saame öelda, et veepinnal toimub valguse peegeldumine. Kuidas peegelduvad üksikud valguskiired ja valguskimbud?
Langemisnurgaks nimetatakse nurka, mis jääb peegeldavale pinnale langenud kiire ja pinna ristsirge vahele (vt joonist). Langemisnurka tähistatakse kreeka tähega alfa (). Peegeldumisnurk on nurk, mis jääb pinnalt peegeldunud kiire ja pinna ristsirge vahele. Peegeldumisnurka tähistatakse kreeka tähega beeta ().
Valguskiirte peegeldumine toimub alati kindla seaduse järgi.
Valguse peegeldumisseadus ütleb, et pinnale langenud kiire langemisnurk on võrdne pinnalt peegeldunud kiire peegeldumisnurgaga.
Lühidalt võib peegeldumisseaduse kohta öelda, et .
Peegeldumisseadust kasutades saab ka teada, kuidas peegelduvad hajuv, paralleelne ja koonduv valgusvihk.
Langev kiir ja peegeldunud kiir asuvad alati ühel tasandil.
| Legendi järgi valmistas Archimedes peeglitest koosneva seadme, mille abil päikesekiirgust koondada. Sel moel olevat ta süüdanud oma kodulinna Sürakuusat ründava Rooma riigi laevastiku. Sellel pildil on kunstniku nägemus sellest sündmusest. | Füüsik teab, et millegi suure põlema panemiseks päikesevalgusega on vaja valgus paljudelt peeglitelt ühte kohta kokku suunata, vaid nii võib tekkida piisav energiavoog. Peeglite asendid sellises skeemis määrab peegeldumisseadus. |
| Ivanpah’ päikeseenergial töötavas elektrijaamas koondavad 173 000 heliostaati valguse kolmele tornides paiknevale veeboilerile, kus tekkiva auru jõul toodetakse elektrienergiat. Elektrijaama võimsus on 392 MW, see on umbes pool Narvas asuva Balti soojuselektrijaama võimsusest. | Heliostaat on seade, mis suunab sellele langeva päikesevalguse alati ühes suunas. Heliostaat koosneb peeglist ning seda suunavast mehhanismist. |
Me näeme esemeid, kui neilt peegeldunud valgus jõuab meie silma. Varasemalt õppisid, et peegeldumisel on valguskiire langemisnurk võrdne peegeldumisnurgaga. Kuid ometi näeme esemeid sõltumata sellest, millise nurga all valgus neile langeb. Miks jõuab valgus esemetelt meie silma? Miks me näeme esemeid värvilisena, ehkki neile langev valgus on valge?
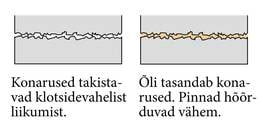
Enamik pindasid ei ole siledad, vaid natuke konarlikud. Isegi paberil, mis tundub küll sile, esinevad lähedalt vaadates väikesed konarused. Peegeldumisseadust kasutades on lihtne aru saada, et konarlik pind peegeldab valgust kõikvõimalikes suundades.
Selliseid konarlikke pindasid nimetatakse mattpindadeks. Mattpind ei peegelda valgust kindlas suunas, vaid hajutab seda.
Valguse hajumine esemete pindade konarustelt võimaldab meil neid esemeid näha – kuna valgus peegeldub igas suunas, satub osa sellest ka meie silma.
Esemeid me näeme vaid juhul, kui sealt peegeldunud valgus jõuab meie silma. Ideaalselt siledat peegeldavat pinda (peeglit) me seega ei näe, paistab vaid see, mida peegel peegeldab. Sarnaselt ei ole tolmu vms osakesteta õhus laserikiirt näha. Kiire nägemiseks tuleb keskkonda lisada väikseid tolmu- vms osakesi, mis valgust meie silma hajutaksid. Õhus sobib selle jaoks udu või suits, vette võib panna näiteks pisut piima.
Vaadates meid ümbritsevaid esemeid, näeme, et nad on erinevat värvi – mõni on punane, teine sinine, kolmas roheline jne. Põhjus, miks me esemeid värvilisena näeme, peitub selles, et kehad ei peegelda kõiki värvi valguseid ühtmoodi – mõnda värvi valgused neelduvad, mõned nõrgenevad, mõned aga peegelduvad peaaegu täielikult. Näiteks punast värvi esemed peegeldavad punast ja neelavad kõiki teist värvi valguseid.
Valgena näivad meile kehad, mis peegeldavad ühtmoodi tagasi kõiki värvi valguseid, mustad on kehad, mis neelavad peaaegu kogu neile langeva valguse, hallid kehad neelavad ja peegeldavad kõiki värvi valguseid.
Tasasel veepinnal võime näha teisel pool kallast olevate puude peegeldust. Veidi teise nurga alt vaadates võime seal näha ka iseennast. Peegelpilte nimetavad füüsikud kujutisteks. Kuidas kujutised tekivad?
Vaatleme mõne eseme, näiteks lambi peegelpilti tasapinnalises peeglis ehk tasapeeglis (vt joonist). Kuidas jõuab valgus lambist silma? Peegeldumisseadust rakendades saame kiire käigu lihtsasti üles joonistada, peame vaid jälgima, et valguskiire langemis- ja peegeldumisnurk oleksid võrdsed. Paneme tähele, et valguskiir tuleb vaatleja silma mitte eseme, vaid peegli poolt. Kui pikendame peeglilt silma suunduvat valguskiirt peegli sisse sama kaugele, kui on tõeline objekt peegli pinnast (vt katkendlik joon joonisel), saamegi eseme peegelpildi ehk kujutise asukoha.
Esemete peegelpilti on võimalik näha ka siis, kui eset ennast ei ole näha. Nii on näiteks võimalik uurida, mis toimub nurga taga või muidu raskesti ligipääsetavas kohas.
Peegeldusi vaadates me peegeldusi tekitavaid peegleid ei näe (vähemalt siis mitte, kui peeglid on puhtad). Seda asjaolu kasutatakse optiliste atraktsioonide ehitamiseks. Piltidel on näha laud, mille all ei ole justkui kedagi, ning peegellabürint, mis justkui ulatub lõpmatusse. Juures on skeem sellest, kuidas need illusioonid tekivad – läbi ühe või mitme peegelduse näeme esimest objekti, mis valgust hajutab.
Vahel räägitakse, et peegel vahetab ära parema ja vasaku külje. Tõepoolest, peeglit vaadates näib, nagu tõstaks peegelpilt vasakut kätt, kui ise peegli ees tõstad paremat. Veidi asja üle järele mõeldes saab selgeks, et kujutisel peeglis on ära vahetatud esimene-tagumine, mitte aga parem-vasak pool. Selles veendumiseks tasub kasvõi tähele panna, et kõik, mis on inimesest vasakul, on ka peegelpildis inimesest vasakul, samas peegli suunas või sellest eemale liikudes teeb kujutis peeglis täpselt vastupidi.
See, mida inimene tajub peegelpildis oma parema käena, on tegelikult vasaku käe kujutis. Peegel ei tee paremast vasakut ja vastupidi. Selle mõistmiseks pöörake ennast niimoodi paremale, et vasak käsi jääb peegli lähedale. Te saate aru, et eespool mainitud mõttelisel pöördel ei ole enam mingit loogilist sisu.
Igapäevaselt on meile tuttav tasapeegel – näiteks see, mis ripub vannitoa seinal. Kuid lisaks sellele on olemas ka veel kumerpeeglid ja nõguspeeglid. Kumer- ja nõguspeeglid erinevad tasapeeglist selle poolest, et nende pind ei ole tasane, vaid on kõver. Seepärast nimetataksegi kumerja nõguspeegleid kõverpeegliteks.
Kumer- ja nõguspeegleid võib vaadelda kui läikiva kera ühte osa.
Kumerpeeglil on läikivaks pinnaks kera välimine pind ning nõguspeeglil kera sisemine pind. Igapäevaselt võime kumer- ja nõguspeeglina vaadelda lusikat, kus lusika üks külg on kumer- ning teine nõguspeegel.
Valguse peegeldumisel kõverpeeglilt kehtib valguse peegeldumisseadus – peeglile langenud kiire langemisnurk α on võrdne peegeldumisnurgaga β.
Kõverpeeglilt peegeldunud kiire joonistamise6ks on vaja joonistada pinna puutuja ja ristsirge. Need tuleb joonistada läbi punkti, kuhu kiir peeglile langes. Kerapinna korral on pinna ristsirgeks raadiuse pikendus. Edasi võime vaadelda pinna puutujat kui tasapeeglit ning vastavalt sellele joonistada peegeldunud kiire.
Kui paralleelne valgusvihk langeb nõguspeeglile, siis kõik kiired koonduvad ühes punktis. Seda punkti nimetatakse peegli fookuseks.
Nõguspeegli peegeldumisomadusi kasutatakse teleskoopides – peeglile langev paralleelne valgusvihk koondatakse peegli fookusesse, kus asub fotosensor, mis sellele langenud valguse registreerib. Kui asetada nõguspeegli fookusesse valgusallikas, näiteks elektripirn, tekib peaaegu paralleelne kiirtekimp. Sellepärast kasutatakse nõguspeeglit näiteks taskulambis ja auto esituledes.
Kumerpeeglile langev paralleelne valgusvihk hajub, kuid kui joonistada hajunud kiirte pikendused, siis need lõikuvad ühes punktis, mis on kumerpeegli fookuseks. Kumerpeegli fookus asub peeglist poole raadiuse kaugusel.
Enamiku autode tahavaatepeeglid on tegelikult kumerpeeglid – kumerpeegel suunab silma väga erinevatest suundadest peeglini jõudvat valgust ning sellepärast vaatenurk laieneb. Eriti kumerad on need peeglid, mida kasutatakse tänavatel „nurga taha“ vaatamiseks ja kauplustes ostjate jälgimiseks.
Valgus nõgus- ja kumerpeeglis
Valguse peegeldumisel kõverpeeglilt kehtib valguse peegeldumisseadus – peeglile langenud kiire langemisnurk on võrdne peegeldumisnurgaga. Kui paralleelne valgusvihk langeb nõguspeeglile, siis kõik kiired koonduvad ühes punktis. Seda punkti nimetatakse peegli fookuseks. Kumerpeeglile langev paralleelne valgusvihk hajub, kuid kui joonistada hajunud kiirte pikendused, siis need lõikuvad ühes punktis, mis on kumerpeegli fookuseks.
Kui suuname laseri kiire vette või klaasplokki, näeme, et valguskiire levimise suund muutub, see justkui murdub. Mis juhtub valguse üleminekul õhust vette? Kas valgus ikkagi ei levi alati sirgjooneliselt?
Ehkki õhk ja vesi mõlemad on läbipaistvad keskkonnad, mõjuvad nad seal levivale valgusele ometigi erinevalt. Täpsemalt, õhul ja veel on erinevad optilised tihedused. Ühesuguse optilise tihedusega keskkonnas, olgu selleks siis õhk või vesi, liigub valgus sirgjooneliselt.
Levides ühest optilise tihedusega keskkonnast teise, valguse levimissuund muutub. Sellist nähtust nimetatakse valguse murdumiseks.
Kirjeldame seda olukorda nüüd täpsemalt. Veele langevat kiirt nimetatakse langevaks kiireks ning nurka valguskiire ja pinna ristsirge vahel langemisnurgaks (tähistatakse kreeka tähega ). Valguskiir, mis levib teise keskkonda (antud näites vette), nimetatakse murdunud kiireks. Nurka murdunud kiire ja pinnaristsirge vahel nimetatakse murdumisnurgaks (tähistatakse kreeka tähega ).
Murdumisnurga suurus sõltub langemisnurgast.
Kui valgus levib optiliselt hõredamast keskkonnast (näiteks õhust) optiliselt tihedamasse keskkonda (näiteks klaasi või vette), siis murdumisnurk on väiksem kui langemisnurk. Vaid siis, kui kiir langeb pinnaga risti, on murdumisnurk ja langemisnurk võrdsed. Mõlemad on siis 0 kraadi.
Valguse langemis- ja murdumisnurgad valguse murdumisel õhust klaasi on antud järgnevas tabelis.
Kui valgus murdub optiliselt tihedamast keskkonnast optiliselt hõredamasse keskkonda, siis on olukord vastupidine – murdumisnurk on alati suurem kui langemisnurk.
Valguse langemis- ja murdumisnurgad valguse murdumisel klaasist õhku on antud järgnevas tabelis.
Valguse murdumisel on optiliselt tihedamas keskkonnas nurk pinna ristsirge ja kiire vahel alati väiksem kui optiliselt hõredamas keskkonnas.
Saame neid kaht tabelit kasutades hinnata klaasplaati läbiva valguskiire levimise suundasid klaasplaadi sees ja sealt väljudes. Tabeleid võrreldes näeme, et klaasplaadile langenud kiir ja plaadist välja murduv kiir liiguvad ühes suunas. Näiteks klaaplaadile 30kraadise nurga all langenud valguskiir ka väljub klaasplaadist 30kraadise nurga all. Klaasplaadi ainus mõju on see, et sellele langenud kiire pikendus teisele poole klaasplaati ja klaasplaati läbinud kiir on omavahel nihkes, nagu näha juuresoleval joonisel.
Kõige lihtsam valguse murdumist kasutav optiline seade on prisma. Valgus murdub klaasprismat läbides kaks korda – prismasse sisenedes ning prismast väljudes. Prismasse sisenedes on valguse murdumisnurk väiksem kui langemisnurk (valgus levib optiliselt hõredamast keskkonnast optiliselt tihedamasse). Prismast väljudes on murdumisnurk suurem kui langemisnurk (valgus levib optiliselt tihedamast keskkonnast hõredamasse).
Kui valgus oma teekonnal esemelt silma murdub, siis tundub meile, et ese asub mujal, kui see tegelikult on. Näiteks paistab kõrvaloleval pildil puu murdununa. Kuidas seda seletada?
Põhjus on meile juba peegeldumise õppimisest tuttav.
Silm suudab hinnata vaid temani jõudnud valguse suunda ning esemete kaugust, aga ei oska kuidagi öelda, kas valgus on vahepeal oma suunda muutnud. Selle asemel näeme eseme kujutist silma sattunud kiirte pikenduste suunas (vaatesiht).
Kuumal päeval võib näha, nagu oleks asfaltteel kaugel eemal veelomp, mis aga kaob, kui sellele läheneda. Kuidas nii?
Kui päike soojendab asfalti, siis alfalt omakorda soojendab tee kohal olevat õhku. Kuna aga sooja õhu optiline tihedus on väiksem kui külmema õhu oma, siis valguskiir muudab levides oma suunda. Selle mõistmiseks kujutame ette, et erinevate temperatuuridega õhukihtide vahel on selge piir. Murdumisseadust rakendades näeme, et valgus kaldub kõrvale ja justkui põrkab väiksema optilise tihedusega piirkonnast (soojemalt õhukihilt) eemale.
Nii on sinakas kuma teel või kõrbes on tegelikult taeva peegeldus asfaldilt (vaata joonist) – silma jõudnud kiirte pikendused on maapinna all. Nähtuseid, kus valguse murdumise tõttu näeme kaugeid esemeid paiknemas kohtades, kus neid tegelikult ei ole, nimetatakse miraažiks.
Sarnaseid loodusnähtuseid võib näha ka väga külmades piirkondades, näiteks Arktikas. Seal on vahel nii, et maa või merepinna lähedal on õhk palju külmem kui sellest veidi kõrgemal. Kuna sel korral on suurema optilise tihedusega piirkond kõrgemal, levivad valguskiired teisipidi kõveralt ja tekivad kaugete objektide miraažid, mis ripuvad justkui kõrgel õhus.
Arktikas esinevad miraažid võivad meile tunduda ehk lahedad, aga maadeavastajatele on nad valmistanud tõsist peavalu. Näiteks 1818. aastal, kui Briti maadeavastaja John Ross otsis läbipääsu Vaikse ja Atlandi ookeani vahel, sisenes ta Lancasteri väina, aga nähes enda ees mägesid, pöördus tagasi. Ta nimetas need mäed Croker’i mägedeks. Järgnevate ekspeditsioonide käigus aga selgus, et neid mägesid ei olegi tegelikult olemas – ilmselt oli Ross näinud miraaži.
Esemete näiv ja tegelik asukoht
Kui valgus oma teekonnal esemelt silma murdub, siis tundub meile, et ese asub oma tegeliku asukohaga võrreldes hoopis mujal. Silm suudab hinnata vaid selleni jõudnud valguse suunda ning esemete kaugust, ent ei oska kuidagi öelda, kas valgus on vahepeal oma suunda muutnud või mitte. Selle asemel näeme eseme kujutist silma sattunud kiirte pikenduste suunas (vaatesiht).
Õhu ja klaasi langemis- ja murdumisnurkade tabelist näeme, et kui langemisnurk klaasis on 39 kraadi, siis peaks murdumisnurk õhus olema 90 kraadi. Mis aga saab siis, kui langemisnurk on suurem kui 39 kraadi?
Reaalses eksperimendis me ei näe mööda keskkondade piiripinda kulgevat valguskiirt, enamus valgust peegeldub hoopis klaasi tagasi.
Selliste nurkade korral valguskiire murdumist enam toimuda ei saa, selle asemel toimub valguse täielik peegeldumine – valgus peegeldub täielikult kahe läbipaistva keskkonna piirpinnalt tagasi.
Valguse täielik peegeldumine saab toimuda ainult siis, kui valgus levib optiliselt tihedamast keskkonnast optiliselt hõredamasse keskkonda, sest vaid sellisel juhul esinevad langemisnurgad, mille korral murdumisnurk peaks olema 90 kraadist suurem või sellega võrdne. Valguse täieliku peegeldumise tingimus on täidetud ka täisnurkses prismas – jooniselt on näha, et valguskiired ei pääse prisma pikemalt tahult välja, vaid peegelduvad. Nii saab prismat kasutada ka peeglina.
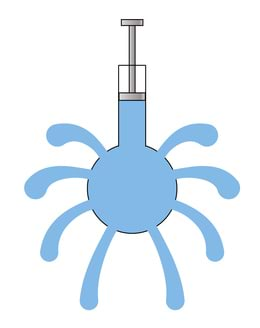
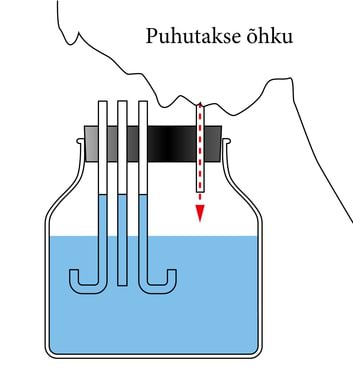
Kui peenikese klaaskiu otsast lasta sisse valgust, siis levib see mööda klaaskiudu ja ei pääse kiust välja. Sarnast katset on ka ise lihtne teha, kui torgata veepudelisse auk ning valgustada tekkinud veejuga. Miks see nii toimub?
Kuna valguskiire langemisnurk klaasi ja õhu piirpinnale on peenikeses klaaskius alati suurem kui 40 kraadi, siis toimub iga kord, kui kiir langeb klaasi pinnale, valguse täielik peegeldumine. Nii jääb kord juba kiudu sisenenud valgus sinna otsekui lõksu.
Optiline kaabel on tänapäeva infotehnoloogias ülimalt oluline – just selliste kaablite kaudu on võimalik ülikiire andmeside, mis on hädavajalik hea internetiühenduse loomiseks.
| Valguse siksakiline tee õhukeses vedelikukihis. Toimub täielik peegeldumine, valgus ei pääse veest välja. | Valguskaablid optiku töölaual – kui valgustame neid ühest otsast, siis jõuab valgus ka teise otsa. Paneme ka tähele, et valguskaablid veidi helendavad. See on sellepärast, et vähesel määral pääseb valgus neist ikkagi välja – nii veejoa kui ka valguskaabli seinal esineb konarusi, mille puhul täieliku peegeldumise tingimus ei kehti. |
Valguse täielik peegeldumine
Valguse optiliselt tihedamast keskkonnast optiliselt hõredamasse keskkonda murdumisel peaks teatud langemisnurgast suuremate nurkade korral murdumisnurk olema suurem kui 90 kraadi. Selliste nurkade korral valguskiire murdumist enam toimuda ei saa, selle asemel toimub valguse täielik peegeldumine – valgus peegeldub täielikult kahe läbipaistva keskkonna piirpinnalt tagasi.
Olete kindlasti märganud, et prilliklaasid ei ole tasapinnalised, vaid kumerad ning erinevatest kohtades erineva paksusega. Vaadates esemeid läbi prillide, paistavad nad meile teistsuguse suurusega, kui nad tegelikult on. Miks see nii on?
Kuna prilliklaaside pind on kumer, siis sealt läbi läinud valgus muudab murdudes oma suunda. Prilliklaasid on konstrueeritud nii, et neid läbiv paralleelne valgusvihk muutub koonduvaks või hajuvaks valgusvihuks. Füüsikas nimetatakse selliseid kehasid läätsedeks.
Läätsede pinnad on tehtud sfäärikujulised. Nende sfääride kõverusraadiused määravad ka läätse omadused. Läätsed võivad olla kas kumerläätsed või nõgusläätsed.
Kumer- ja nõgusläätse omadusi on kõige lihtsam seletada, kui kujutame neid koosnevana lõigatud tippudega prismadest ning ühest klaasplaadist keskel, mis ligikaudselt jäljendavad läätse kuju (vt joonist). Sellisel juhul – näiteks kumerläätse puhul – ülemistele prismadele langenud kiired murduvad allapoole, keskmist klaastahvlit läbivad kiired ei murdu ning alumist klaasprismat läbinud kiired murduvad ülespoole. Sealjuures on klaasprismad valitud sellised, et kõik paralleelse kiirtekimbu kiired koonduvad punktis F. Nõguspeegli korral saab arutleda analoogiliselt.
Läätsede kirjeldamiseks on vaja teada olulisi läätsi iseloomustavaid mõisteid.
- Läätse optiliseks peateljeks nimetatakse läätse pindasid moodustavate sfääride keskpunkte ühendavat sirget (vt joonist lehekülje keskel).
- Läätse optiliseks keskpunktiks O nimetatakse läätse keskel optilisel peateljel asetsevat punkti.
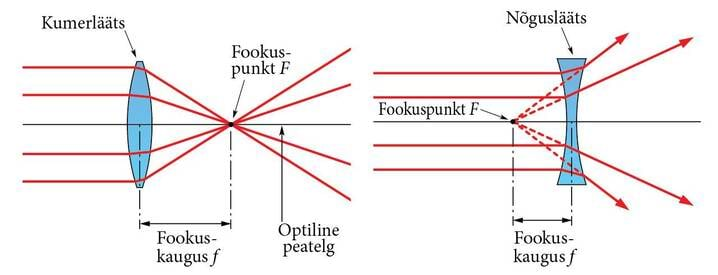
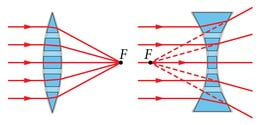
- Kumerläätse fookuseks F nimetatakse punkti, kus koondub läätsele langev paralleelne valgusvihk.
- Fookuskauguseks nimetatakse fookuse F ja optilise keskpunkti O vahelist kaugust. Fookuskaugust tähistatakse tähega f. Nõgusläätse korral nimetatakse läätse fookuseks punkti, kus koonduvad läätse läbinud hajunud kiirte pikendused. Kuna hajunud kiirte pikendused koonduvad teisel pool läätse, on nõgusläätse fookuskaugus kokkuleppeliselt miinusmärgiga.
- Läätse optiliseks tugevuseks (D) nimetatakse läätse fookuskauguse pöördväärtust:
Seega
Läätse optilise tugevuse mõõtühikuks on dioptria (lühend dpt). Üks dioptria on sellise läätse optiline tugevus, mille fookuskaugus on 1 meeter: 1 dpt = 1/1 m. Läätse optilise tugevuse määramiseks tuleb mõõta läätse fookuskaugus meetrites ning arvutada selle pöördväärtus
Kumerläätse fookuskauguse määramiseks tuleb leida koht, kus läätsele langenud paralleelne valgusvihk muutub punktiks. Paralleelse valgusvihu tekitab näiteks päike – lääts tuleb asetada risti päikesekiirtega ning viia pinnast sellisele kaugusele, kus lääts tekitab pinnale valgustäpi. Läätse ja pinna vaheline kaugus ongi sellisel juhul kumerläätse fookuskaugus.
Tavaliselt kasutatakse optilistes seadmetes mitut läätse korraga. Kahest või mitmest lähestikku asetsevast läätsest koosnevat optilist süsteemi nimetatakse liitläätsedeks. Liitläätse optiline tugevus on võrdne üksikute läätsede optiliste tugevuste summaga:
Näiteks kui liitlääts koosneb kahest kumerläätsest, mille optilised tugevused on vastavalt 2 dpt ja 3 dpt, siis nendest läätsedest koosneva liitläätse optiline tugevus on 5 dpt.
Kumer- ja nõgusläätsed
Läätsede pinnad on sfäärikujulised ja muudavad seetõttu neid läbiva paralleelse valgusvihu koonduvaks (kui tegu on kumerläätsega) või hajuvaks valgusvihuks (kui tegu on nõgusläätsega).
Läätse optiline peatelg ja optiline keskpunkt
Läätse optiliseks peateljeks nimetatakse läätse pindasid moodustavate sfääride keskpunkte ühendavat sirget. Läätse optiliseks keskpunktiks nimetatakse läätse keskel optilisel peateljel asetsevat punkti.
Läätse fookus, fookuskaugus ja optiline tugevus
Kumerläätse fookuseks nimetatakse punkti, kus koondub läätsele langev paralleelne valgusvihk. Nõgusläätse korral nimetatakse läätse fookuseks punkti, kus koonduvad läätse läbinud paralleelse valgusvihu hajunud kiirte pikendused.
Fookuskauguseks nimetatakse fookuse ja optilise keskpunkti vahelist kaugust. Kuna hajunud kiirte pikendused koonduvad teisel pool läätse, on nõgusläätse fookuskaugus kokkuleppeliselt miinusmärgiga.
Läätse optiliseks tugevuseks () nimetatakse läätse fookuskauguse pöördväärtust:
Seega
Asetame kumerläätsest ühele poole põleva küünla ning teisele poole valge ekraani. Ruum olgu hämar või päris pime. Muutes küünla, läätse ja ekraani omavahelist asendit, on võimalik tekitada olukord, kus ekraanile tekib küünlaleegi kujutis.
Küünlaleegi kujutis ei teki igasuguse küünla, ekraani ja läätse asendi korral. Muutes küünla kaugust läätsest, peame terava kujutise saamiseks muutma ka ekraani asukohta läätse suhtes.
Sõltuvalt küünla, läätse ja ekraani omavahelisest asendist on ekraanile tekkinud küünla kujutise suurus erinev. Ekraanile tekkinud kujutist nimetatakse tõeliseks kujutiseks.
Ülevaatlikult on selles kujutise vaatlemise katses tekkivad olukorrad esitatud järgneval joonisel:
| Nihutades küünla täpselt kahe fookuskauguse kaugusele, tekib kujutis samuti kahe fookuskauguse kaugusele ning on täpselt sama suur kui küünal, kuid pööratud. | Kui küünal asetada ühe ja kahe fookuskauguse vahele, siis tekib kujutis kaugemale kui kaks fookuskaugust ning on esemest suurem, kuid jääb siiski pööratuks. |
Teatud juhtudel küünla kujutis küll tekib, aga seda ei ole võimalik ekraanil vaadelda. Sellist kujutist nimetatakse näivaks kujutiseks. Näiva kujutise vaatlemiseks on vaja veel üht läätse, selliseks lisaläätseks võib olla ka inimese silm. Kui küünal viia läätsele lähemale kui üks fookuskaugus, siis ekraanile küünla kujutist tekitada pole võimalik. Kujutist näeme ainult siis, kui vaatame seda silmaga läbi läätse.
Üldistusena võime öelda, et kumerläätse tekitatud tõeline kujutis on alati pööratud ning võib olla nii suurendatud kui ka vähendatud. Seevastu kumerläätse tekitatud näiline kujutis on alati samapidine ning suurendatud. Seega saab kumerläätse kasutada väikeste esemete vaatlemiseks, kui esemed asetada kumerläätse ja fookuse vahele. Väikese fookuskaugusega kumerläätsi nimetatakse ka luupideks.
Nõgusläätsega ei õnnestu meil ühelgi juhul tekitada kujutist ekraanile, seda on võimalik vaadelda ainult silmaga läbi läätse.
Seega nõguslääts tekitab alati näiva kujutise. Nõgusläätse tekitatud kujutis on alati vähendatud ning samapidine.
Gümnaasiumis me õpime, et eseme kaugus läätsest, kujutise kaugus läätsest ja läätse fookuskaugus on omavahel seotud ning matemaatiliselt seob need suurused omavahel läätse valem
kus a on eseme kaugus läätsest, k kujutise kaugus läätsest ning f läätse fookuskaugus. Proovi, kas oskad selles alajaotuses kirjeldatud olukorrad ka sellest valemist välja lugeda.
Eelmises peatükis uurisime kujutise tekkimist katseliselt. Läätse tekitatud kujutise asukohta on võimalik teada saada ka joonisel kiirte käiku konstrueerides.
Selleks joonistame kõigepealt läätse koos optilise peatelje ning fookustega. Läätse kujutame joonise lihtsustamiseks kokkuleppeliselt nooltega.
Kui lääts on joonistatud, tuleb joonisele kanda ka ese, mille kujutist me konstrueerime. Pärast seda peame joonistama vähemalt kahe ühest ja samast eseme punktist lähtuva kiire tee läbi läätse.
Kuna meile piisab vaid kahe kiire joonistamisest, peaksime valima need, mida on mingil põhjusel lihtne joonistada. Sellised kiired on järgmised.
- Kiir, mis läbib läätse keskpunkti. See kiir ei muuda oma suunda (joonisel kiir 1).
- Kiir, mis on algselt paralleelne läätse optilise peateljega ning läbib seega pärast läätse läbimist selle fookust (joonisel kiir 2).
- Kiir, mis läbib enne läätse selle fookust ning on seega pärast läätse läbimist paralleelne optilise peateljega (joonisel kiir 3).
Selliselt saame konstrueerida ühe punkti kujutise.
Kui esemeks on sirge, siis saab tema kujutist joonistada nii, et leitakse sirge mõlema otsa kujutise asukohad, mis annavadki noole kujutise asukoha – kui ese oli algselt sirge, siis on ka kujutis sirge.
Kui ese on ruumiline kujund, tuleks sarnaselt konstrueerida kõigi eseme iseloomulike punktide (tavaliselt kõik nurgad) kujutised. Kujutise konstrueerimisel tasub meeles pidada, et kui ese oli algselt paralleelne läätsega, siis on ka kujutis paralleelne läätsega (lõigud AB ja A'B' on paralleelsed).
Kujutise konstrueerimine
Alustuseks tuleb teha joonis. Vali välja eseme olulised punktid (sirge otsad, nurgad) ja joonista igast sellisest punktist vähemalt kaks kiirt läbi läätse. Kiirte lõikumiskohas tekib punkti kujutis, selliste punktide ühendamisel saad eseme kujutise. Kiirte joonistamisel tuleb valida sellised, mida on lihtne joonistada - kiir läbi keskpunkti, optilise teljega paralleelne kiir, kiir mis läbib enne läätse fookust.
Silmad on inimesele väga tähtsad, sest nägemise kaudu saame ümbritsevast kõige rohkem informatsiooni. Silma tööpõhimõtte mõistmiseks ei pea me tundma kõiki selle anatoomilisi iseärasusi. Piisab, kui teame, et silmas on lääts, mis tekitab esemetest silma võrkkestale ümberpööratud ja vähendatud kujutise.
Silma võrkkesta moodustavad kahte liiki nägemisrakud – kolvikesed ja kepikesed. Nägemisrakkudes toimub valguse mõjul keemiline reaktsioon, mis annab signaali peaajusse. Peaaju suudab erinevatelt nägemisrakkudelt tulnud signaalid ühtseks pildiks kokku panna.
Inimene saab silmaläätse optilist tugevust vastava lihase abil muuta – lähedale vaadates muutub silmalääts kumeramaks ning läätse fookuskaugus on väiksem, kaugele vaadates on lääts õhem ning fookuskaugus on siis suurem. Selliselt saame tekitada võrkkestale terava kujutise erinevate eseme kauguste korral. Silmaläätse fookuskauguse muutmine toimub automaatselt – me ei pea seda teadlikult ise muutma.
Normaalnägija näeb selgelt nii lähedal kui ka kaugel asetsevaid esemeid. Silmaläätse pingutav lihas muudab silmaläätse fookuskaugust ja silma võrkkestale tekib alati terav kujutis. Siiski, kõikide inimeste läätse pingutav lihas ei suuda silmaläätse kuju muuta nii, et võrkkestale tekib alati terav kujutis.
Lühinägija näeb selgelt lähedal asetsevaid esemeid.
| Probleem Kaugele vaadates ei suuda silma lääts oma optilist tugevust (paksust) piisavalt vähendada, kujutis tekib silma läätse ja võrkkesta vahele ning võrkkestale tekkiv kujutis ei ole terav. | Lahendus. Lühinägija vajab kaugele vaatamiseks nõgusläätsedega prille, mis aitavad terava kujutise tekitada võrkkestale. |
Kaugnägija näeb selgelt kaugel asetsevaid esemeid.
| Probleem Lähedale vaadates ei suuda silma lihas silma läätse optilist tugevust piisavalt suurendada, terav kujutis tekib võrkkesta taha ning võrkkestale tekkiv kujutis ei ole terav. | Lahendus Kaugnägija vajab lähedale vaatamiseks kumerläätsedega prille, mis aitavad tekitada terava kujutise võrkkestale. |
Lühinägijad on enamasti noored inimesed, kes vajavad kaugele vaatamiseks prille. Kaugnägijad on enamasti vanad inimesed, kes vajavad näiteks raamatu lugemiseks prille.
Prilliklaaside number – näiteks +0,5 või –2,0 – näitab prilliläätse optilist tugevust. Negatiivse tugevusega prillid on nõgusläätsedega prillid, mida vajavad lühinägijad. Positiivse tugevusega prillid on kumerläätsedega prillid, mida vajavad kaugnägijad.
Inimesed teaduspärast küll näevad hämaras ruumis, kuid ei suuda seal värve eristada. See on sellepärast, et vaid kepikesed suudavad reageerida väga vähesele valgusele, aga nende edastatav pilt on loomult hall. Värvilist pilti edastavad kolvikesed, aga kolvikesed ei reageeri nõrgale valgusele. Seetõttu suudab inimene nõrgas valguses küll näha, aga mitte värve eristada.
Paljud loomad näevad pimedas inimestest paremini. See tuleb sellest, neil on otse võrkkesta taga tapetum lucidum’i nime kandev kile, mis peegeldab võrkkestast läbi läinud valguse tagasi võrkkesta, suurendades sel viisil võrkkestas neelduva valguse hulka. Tapetum lucidum on ka põhjus, miks loomade silmad öösel helendavad, st valgust tagasi peegeldavad.
Silm
Silmas on lääts, mis tekitab esemetest silma võrkkestale ümberpööratud ja vähendatud kujutise. Inimene saab silmaläätse optilist tugevust vastava lihase abil muuta. Selliselt saame tekitada võrkkestale terava kujutise erinevate eseme kauguste korral.
Lühi- ja kaugnägelikkus, prillid
Normaalnägija näeb selgelt nii lähedal kui ka kaugel asetsevaid esemeid. Lühinägija näeb selgelt lähedal asetsevaid esemeid, kaugete esemete vaatlemisel tekib kujutis võrkesta ette. Kaugnägija näeb selgelt kaugel asetsevaid esemeid, lähedal asuvaid esemeid vaadeldes tekib kujutis võrkkesta taha.
Lühi- ja kaugnägelikkust korrigeeritakse vastavalt hajutavate ja koondavate läätsedega (prillid). Prillide ülesanne on tekitada olukord, kus kujutis tekiks võrkkestale.
Fotoaparaat töötab põhimõtteliselt samamoodi nagu inimese silm. Ka fotoaparaadis on läätsed. Need tekitavad esemest vähendatud ja ümber- pööratud kujutise fotoaparaadi valgustundlikule sensorile (valgustundlikule ekraanile), mis muudab temale langenud valguse elektrisignaalideks, mis omakorda töödeldakse pildiks.
Tänapäeval puutume kõige sagedamini kokku miniatuursete kaameratega, nagu neid leiab näiteks nutitelefonides. Eriolukordades, näiteks nõrgas valguses või väga lähedasi või väga kaugeid objekte pildistades, ei saa siiski läbi ilma targemate kaamerate ja spetsiaalsete objektiivideta.
Et kujutis oleks terav, tuleb läätsed sensorist õigele kaugusele seada. Suurtel objektiividel on aga fokusseerimiseks olemas spetsiaalne rõngas, mida pöörates läätsed sensorist kaugemale ja lähemale nihkuvad. Sellel pildil on osad objektid teravad, osad udused, st fookusest väljas. Teadlik fotograaf oskab hea fotoaparaadi abil teha ka nii, et kõik objektid oleksid teravad, loomulikult ka seda, et vaid keskmine objekt on terav. Väidetavalt saab iPhone 7 sama asjaga hakkama digitaalselt oma kahe kaamera pilte üheks töödeldes.
Mikroskoop on optikariist, mis võimaldab näha väga väikeste esemete suurendatud kujutist. Kaasaegsete valgusmikroskoopidega on võimalik tekitada esemest rohkem kui tuhandekordne suurendus. Seeläbi saab vaadata esemeid, mida palja silmaga pole võimalik näha. Mikroskoobis tekitavad kujutise kaks kumerläätse, mida nimetatakse objektiiviks ja okulaariks. Objektiiv on lääts, mis asub vaadeldava eseme pool. Okulaariks nimetatakse seda läätse, mis asub silma pool. Mikroskoop võimaldab vaadata esemest rohkem kui 1000kordselt suurendatud kujutist.
Ka tavaliste fotoaparaatidega on võimalik teha väga väikestest objektidest pilte. Idee on lihtne – et fotoaparaadi tööpõhimõte on sama, mis inimese silmal, peaks ka fotoaparaadi sensorile tekkima suurendatud kujutis siis, kui fotoaparaat „vaatab” läbi luubi. Tõepoolest, lähedalt, vaid mõne sentimeetri kauguselt pildistamiseks on objektiividele võimalik paigaldada lisalääts.
Fotoaparaat
Fotoaparaadis tekitab läätsede süsteem esemest vähendatud ja ümberpööratud kujutise valgustundlikule sensorile (ekraanile), mis muudab langenud valguse elektrisignaalideks, mis omakorda töödeldakse pildiks. Tänapäevased fotoaparaadid sisaldavad mitmeid tehnoloogiaid, mis parendavad pildi kvaliteeti erinevates situatsioonides, ent oma põhiolemuselt on see ikkagi läätsega ekraanile kujutise tekitamine.
Mikroskoop
Mikroskoop tekitab kuni tuhat korda suurendatud näivkujutise, mida on võimalik vaadelda silma või kaameraga. Mikroskoobi põhiosadeks on objektiiv ja okulaar. Objektiiv (väike fookuskaugus) tekitab suurendatud ja pööratud tõelise kujutise. Okulaar (suurem fookuskaugus) on luup, millega vaadeldakse objektiivi tekitatud tõelist kujutist.
Teleskoop on seade, mida kasutatakse kaugete esemete vaatamiseks. Lihtsamad teleskoobid koosnevad kahest kumerläätsest, mida nimetatakse samuti nagu mikroskoobigi puhul objektiiviks ja okulaariks. Milline on teleskoobi tööpõhimõte?
Kaugete esemete vaatamisel võib lugeda objektiivile langenud kiired paralleelseteks ja need koonduvad seega esimese läätse fokaaltasandil. Teleskoobi puhul langeb okulaari fookus praktiliselt kokku objektiivi fookusega, mistõttu ka teleskoobist väljunud kiired on paralleelsed. Tekkinud paralleelsed kiirtekimbud koondab kujutiseks silma lääts.
Nüüd võiks küsida, et kui me alustasime ja lõpetasime paralleelsete kiirtekimpudega, siis miks teleskoop ikkagi suurendab? Vastus peitub suunas, kust silma jõudnud paralleelsed kiirtekimbud tulevad. Me näeme tähti selles suunas, mitte seal, kus nad tegelikult on.
Muide, tähed on teleskoobis alati täpid, st ükskõik kui suurt teleskoopi me kasutame, tähe pinda me sellega uurida ei saa, ainult tähe värvust. Päike on siin muidugi üks ja ainuke erand.
Suuremates teleskoopides ei kasutata objektiividena mitte läätsesid, vaid nõguspeegleid. Üheks tuntumaks peegelteleskoobiks on Hubble’i kosmoseteleskoop. Aga Maa orbiidil tiirleb näiteks ka Kepleri teleskoop ning otsib Maa-sarnaseid planeete.
Miks näeb kosmosesse lennutatud teleskoobiga isegi täiesti selge ilmaga paremini kui maapealsetega? Nüüd, kui oled optika kursuse läbinud, oskad sellele küsimusele ka ise vastuse välja pakkuda. Piisab, kui meenutad, et sooja ja külma õhu murdumisnäitajad on erinevad ning sooja ja külma õhumassi piiril muudab valgus oma suunda.
Teleskoop
Teleskoop on seade, mida kasutatakse kaugete esemete vaatamiseks. Lihtsamad teleskoobid koosnevad kahest kumerläätsest, mida nimetatakse objektiiviks (suur fookuskaugus) ja okulaariks (väike fookuskaugus). Objektiiv tekitab oma fokaaltasandile tõelise pöördkujutise, okulaar töötab kui luup, millega seda kujutist vaadeldakse.
Google’i prillid on liitreaalsusega prillid, mille abil reaalsele keskkonnale lisatakse virtuaalne – reaalsust rikastatakse andurite abil saadud infoga nii, et inimene näeb rohkem kui tegelikus maailmas olemas on. Kuidas tekitavad need prillid silma ette sellise virtuaalse infoekraani?
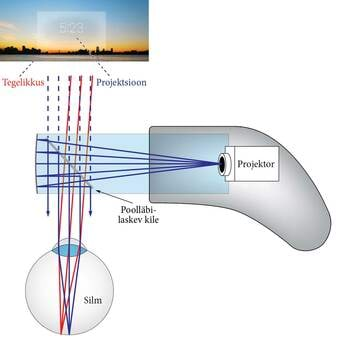
Prillide sangades on projektor. Sangadest ulatub välja klaasist kuup. Kuubi sees on näha kile, mis on valgusele „poolläbilaskev“, st osa valgust pääseb sealt läbi, osa peegeldub. Klaaskuubi ots on kaetud alumiiniumikihiga ja peegeldab sellele langenud valguse kuupi tagasi (vt pilti).
Poolläbilaskva kile või ka lihtsalt klaasplaadiga saab tekitada näiva kujutise reaalsete objektide „peale“ või kõrvale. Selles veendumiseks vaadake õhtul hämaras läbi akna õue. Lisaks õues olevate objektide kujutistele näete aknaklaasile tekkiva peegelduse kaudu kindlasti ka toas toimuvat. Just samamoodi „riputataksegi“ läbi prillide vaatava silma ette lisaks reaalsele pildile ka projektorist tulev infoekraan.
Mida neil piltidel tähele panna?
Me võime piirduda sellise lihtsa seletusega, kuid lähemalt vaadeldes tekib küsimusi juurde. Näiteks peab klaaskuubi peegeldav ots olema sfääriline, st moodustama seestpoolt vaadatuna nõguspeegli – kui suur peaks aga olema selle kõverusraadius ja fookuskaugus? Kui kaugele silmas peaks tekkima infoekraani näiv kujutis, et ekraani vaadates end mugavalt tunda? Kuidas on neis prillides välditud kujutise moonutusi? Google’i prillide mudeli saab üsna lihtsate vahenditega ise teha, seega on nende küsimuste uurimiseks olemas hea võimalus.
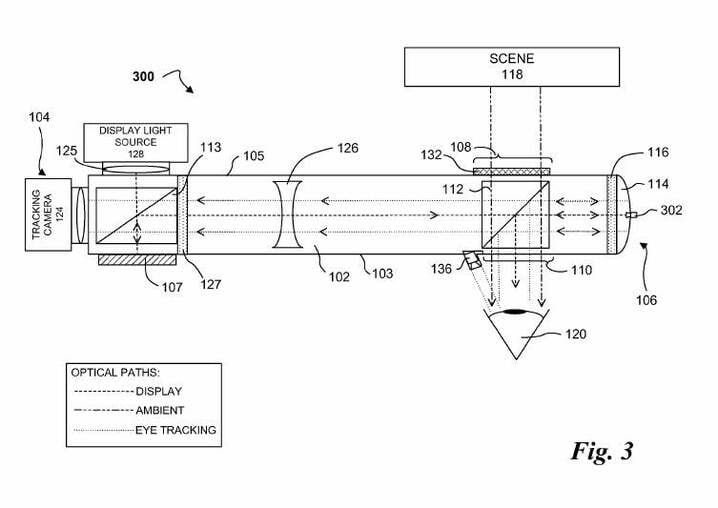
Lõpuks üks realistlikum skeem, kus peal palju lisakomponente, aga mille põhiline idee on seesama.
Keha mehaaniliseks liikumiseks nimetatakse selle asukoha muutumist teiste kehade suhtes. Keha liikumist iseloomustab liikumise kiirus. Kuidas nii?
Kiiruse arvutamisega oled juba kokku puutunud. Kiiruseks nimetatakse füüsikalist suurust, mis näitab, kui pika tee läbib keha mingi ajavahemiku jooksul:
ehk
Vaatleme nüüd inimese liikumist sõitvas rongis. Milline on inimese kiirus, kui ta liigub vaguni ühest otsast teise?
Sellele küsimusele saame anda kaks vastust. Me saame leida inimese kiiruse vaguni suhtes, kui teame vaguni pikkust ja aega, mis kulub selle läbimiseks. Me saame leida ka inimese kiiruse maapinna suhtes. Kui inimene liigub rongis sõidusuunas, on tema kiirus maapinna suhtes suurem rongi liikumise kiirusest, kuna lisaks enda kõndimisele liigub inimene ka koos rongiga edasi.
Pildil liigub inimene rongi suhtes kiirusega vi=3m/s ning rong liigub maapinna suhtes kiirusega vr=20m/s. Inimese kiiruse leidmiseks maapinna suhtes peame need kiirused liitma:
Kui inimene liigub kiirusega 3m/s rongi liikumisele vastassuunas, siis tuleb inimese kiiruse leidmiseks maapinna suhtes rongi kiirusest lahutada inimese liikumise kiirus rongi suhtes, kuna inimene ja rong liiguvad vastassuundades. Inimene liigub seega maapinna suhtes kiirusega
Keha kiirus on alati suhteline, kuna keha kiirust väljendatakse alati mingi teise keha suhtes. Kui pole mainitud, mis keha suhtes me kiiruse peame leidma, mõeldakse enamasti kiirust maapinna suhtes.
Mehaanilisi liikumisi võib liigitada kaheks: ühtlane sirgjooneline liikumine ja muutuv liikumine. Ühtlase sirgjoonelise liikumise korral keha kiirus ei muutu. Selliste liikumiste erijuht on paigalseis. Muutuva liikumise korral muutub keha kiirus või suund.
Vaatleme liikumist kodust kooli. Kool asub kodust 2km kaugusel ning meil kulus kooli jõudmiseks pool tundi. Kogu teekonna vältel ei olnud meie kiirus ühtlane, kuna vahepeal tuli peatuda, et üle tee minna. Meie liikumine kodust kooli oli mitteühtlane.
Mitteühtlase liikumise korral saame arvutada keskmise kiiruse, kui jagame läbitud teepikkuse liikumiseks kulunud ajaga. Keskmise kiiruse arvutamiseks tuleb arvestada liikumise aja hulga sisse ka peatusteks kulunud aeg. Selle näite puhul on kodust kooli liikumise keskmine kiirus
Näiteülesanne
Kiirusega v1=99km/h sõitva auto juht märkab temale lähenevat autot ning käivitab stopperi. sekundi pärast autod kohtuvad. Kui kaugel oli lähenev auto, eeldades, et ta sõitis kiirusega v2=90km/h?
Lahendus
Vaatleme liikumisi kiirusega sõitva auto suhtes. Sellisel juhul läheneb sõitvale autole auto kiirusega
Teades, mis aja pärast autod kohtusid, saame leida, kui kaugel nad teineteisest olid.
Andmed
v1=90km/h=25m/s
v2=99km/h=27,5m/s
t=40s––––––––
s−?
Arvutused
Vastus. Lähenev auto oli alguses 2,1km kaugusel.
Mehaaniline liikumine, keskmine kiirus
Mehaanilisi liikumisi võib liigitada kaheks: ühtlane sirgjooneline liikumine ja muutuv liikumine. Ühtlase sirgjoonelise liikumise korral keha kiirus ei muutu. Muutuva liikumise korral muutub keha kiirus või suund.
Mitteühtlase liikumise korral saame arvutada keskmise kiiruse, kui jagame läbitud teepikkuse liikumiseks kulunud ajaga.
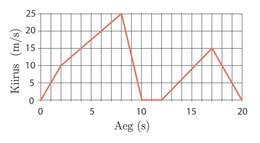
Mõnikord on mõistlik ja ülevaatlik kujutada liikumisi graafiliselt, näidates ära, kuidas läbitud teepikkus sõltub ajast. Sellist graafikut me nimetame teepikkuse graafikuks.
Mõnikord ei näidata liikumise graafilisel kujutamisel teepikkuse muutumist ajas, vaid kiiruse muutumist ajas – selliseid graafikuid me nimetame kiiruse graafikuks.
Vaatleme I lõiku. Kiirus muutub seal ühtlaselt (graafik on sirgjoon) 0 m/min kuni 100 m/min. Kuna tegemist on ühtlaselt muutuva kiirusega liikumisega, saame keskmine kiiruse sellel lõigul arvutada aritmeetilise keskmisena: (0 + 100)/2 = 50 m/min.
Näiteülesanne
Matkaja liikumist esimese kümne minuti jooksul kajastab üleval toodud teepikkuse graafik. Vasta järgmistele matkajat puudutavatele küsimustele.
- Millise ajavahemiku jooksul liikus matkaja kõige kiiremini?
- Mitu minutit matkaja vahepeal järjest puhkas?
- Milline oli matkaja keskmine kiirus kogu teekonna vältel?
- Kui palju oli matkaja keskmine kiirus pärast puhkust väiksem/suurem kui enne puhkust?
- Miks keskmised kiirused enne ja pärast puhkust on suuremad kui kogu matka keskmine kiirus?
Lahendus
- Kõige kiiremini liigub matkaja sellel lõigul, kus graafiku tõus on kõige suurem. Graafikut lugedes saame teada, et esimese ja teise minuti jooksul läbis matkaja minutis meetrit, mis on ka kõige kiirem lõik kogu matka jooksul. Ülejäänud matka vältel matkaja nii kiiresti enam ei liikunud. Ajavahemikul 6-8 minutit läbis matkaja ühes minutis meetrit.
- Matkaja puhkas selles ajavahemikus, kus graafiku tõus on (graafik on horisontaalne). Graafikult näeme, et matkaja puhkas minutit ajavahemikus 4-6 minutit.
- Keskmise kiiruse saame leida, kui jagame kogu läbitud teepikkuse selleks kulunud ajaga.
Andmed
s=720m
t=10min=600s––––––––––––––––––––
v−?
Arvutused
Vastus. Matkaja keskmine kiirus kogu matka vältel oli 1,2m/s. - Matkaja puhkas ajavahemikus 4-6 minutit. Leiame matkaja keskmise kiiruse ajavahemikus 0-4 minutit ning keskmise kiiruse ajavahemikus 6-10 minutit.
Andmed
s1=420m
s2=720m–420m=300m
t2=4min=240s–––––––––––––––––––
v1−?
v2−?
Arvutused
Vastus. Matkaja keskmine kiirus oli pärast puhkust väiksem kui enne puhkust. - Kogu matka keskmise kiiruse arvutamise hulka arvestati ka puhkuseks kulunud aeg, mistõttu on kogu matka keskmine kiirus väiksem kui matkaja kiirused enne ja pärast puhkust.
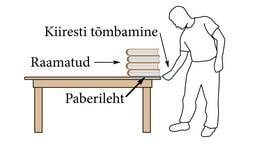
Asetame raamatute kuhja (või ka näiteks veeklaasi) paberilehe peale. Tõmmates paberit järsult ja kiiresti, jäävad raamatud paigale ning paber libiseb nende alt ära. Kui aga liigutada paberit aeglaselt ja ettevaatlikult, siis liiguvad raamatud paberiga kaasa. Miks jäävad raamatud siis paigale, kui paberit järsult tõmmata?
Kui raamatud hakkavad paberiga kaasa liikuma, siis sellepärast, et me mõjutame neid paberi kaudu.
Aga kirjeldatud katses ilmneb ka raamatute inertsus – nad püüavad säilitada oma liikumisolekut, st jääda paigale.
Nii keha kiiruse suurendamiseks kui ka vähendamiseks tuleb rakendada jõudu, kusjuures jõud peab olema seda suurem, mida järsemalt me tahame kiirust muuta. Raamatute kuhja kiiruse järsuks suurendamiseks peaksime rakendama väga suurt jõudu ja seda ei ole võimalik teha paberilehte sikutades – pigem tuleb paber raamatute alt välja või rebeneb, kui et raamatud nihkuvad.
Niisiis, kehade omaduse tõttu, mida kutsutakse inertsuseks, ei saa nende kiirust muuta hetkeliselt, selleks kulub alati aega. Keha inertsust iseloomustab tema mass – mida suurem on keha mass, seda inertsem on keha ja seda raskem on selle kiirust muuta.
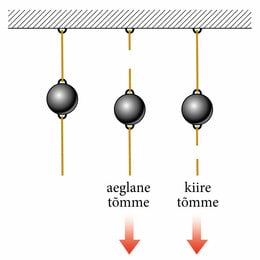
Teeme veel ühe katse. Kinnitame kuuli niidiga lae külge. Kuuli alla on kinnitatud teine täpselt samasugune niit. Kumb niit katkeb, kui alumist niiti allapoole tõmmata?
Selgub, et see, kas katkeb ülemine või alumine niit, sõltub sellest, kui järsult niiti tõmmata.
Olukorra analüüsimiseks peaksime aru saama, kummale niidile, kas alumisele või ülemisele, mõjub suurem jõud. Seda teades saame ka otsustada, kumb niit katkeb.
Tõmmates alumist niiti aeglaselt ja rahulikult, katkeb ülemine niit. Sellisel juhul mõjub alumisele niidile ainult tõmbejõud, seevastu ülemisele niidile mõjub lisaks tõmbejõule veel ka kuuli raskus. Järelikult mõjub ülemisele niidile suurem jõud kui alumisele ja ülemine niit puruneb. Kuuli inertsus siin suurt rolli ei mängi, sest talle antakse oma liikumisoleku muutmiseks piisavalt aega.
Tõmmates niiti järsult, katkeb alumine niit. See juhtub nii sellepärast, et kuul nagu ka iga teine keha püüab säilitada oma liikumisolekut ja jääda liikumatult rippuma. Järsult niiti tõmmates üritame järsult kuuli kiirust muuta. Aga järsuks kiiruse muutmiseks on vaja rakendada väga suurt jõudu. Alumine niit ei pea sellele vastu ja katkeb. Kui suur on jõud, mis mõjub ülemisele niidile? Kuna järsult alumist niiti tõmmates katkeb see enne, kui kuul liikuma jõuab hakata, siis ülemisele niidile mõjuv jõud jääb peaaegu muutumatuks, igal juhul on see jõud väiksem kui see, mis mõjub alumisele niidile.
Kehade inertsus on kehade omadus säilitada oma liikumisolekut – kas jääda paigale või liikuda ühtlaselt ja sirgjooneliselt.
Kehade inertsus avaldub eriti ilmekalt, kui üritame ääreni täidetud laia veeanumat ühest kohast teise kanda. Vesi loksub siis üle serva vähimagi kiiruse muutuse korral – kui kiirendame veidi, üritab vesi kausist „maha jääda“, kui aeglustame, üritab vesi jätkata liikumist endise kiirusega.
Kehade inertsus mängib meie igapäevaelus väga suurt rolli ja me oskame sellega arvestada ka siis, kui me vastavat füüsikaseadust sõnastada ei oska. Me teame, et suurema massiga palli on raskem kaugele visata, uisutaja liugleb jääl ka siis, kui ta parajasti hoogu ei anna, jalgrattaga sõites tuleb õigel ajal pidurdama hakata, muidu on kokkupõrge vältimatu, jne.
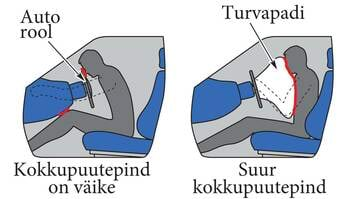
| Kui kehad ei oleks inertsed, ei oleks liiklusõnnetused probleemiks – põrkuvad autod muudaksid hetkega oma liikumisolekut ja jääksid seisma ilma, et üksteisele kahju teeksid. Reaalses kokkupõrkes ei ole niisugune asi võimalik – laupkokkupõrkes jätkavad autode tagumised otsad liikumist ka siis, kui esimesed otsad juba seisavad. | Võidusõiduautode edu võistlustel sõltub paljuski sellest, kui kiiresti nad suudavad oma liikumisolekut muuta. Sellepärast püütakse nende mass võimalikult väike hoida – mida väiksem mass, seda väledam auto. |
Kehade inertsus
Kehade inertsuseks nimetatakse nähtust, kus kehad püüavad säilitada oma liikumisolekut. Keha inertsust iseloomustab tema mass – mida suurem on keha mass, seda inertsem on keha ja seda raskem on selle kiirust muuta. Kehade inertsuse omaduse tõttu ei saa nende kiirust muuta hetkeliselt, selleks kulub alati aega.
Põrandale asetatud pall seisab paigal, kui miski teda ei mõjuta. Pall hakkab liikuma alles siis, kui me seda tõukame, nagu seda juba oleme näinud kehade inertsuse omadusega tutvudes. Teame ka, et liikuma lükatud pall ei veere kuigi kaua, vaid jääb mõne aja pärast seisma. Kuidas neid nähtusi seletada?
Sellele küsimusele vastamiseks peame uurima kehade vastastikmõju seaduspärasusi. Varasemast teame, et
- keha püsib paigal või liigub ühtlaselt ja sirgjooneliselt, kui seda ei mõjuta teised kehad;
- keha kiirus võib muutuda ainult siis, kui seda mõjutavad teised kehad.
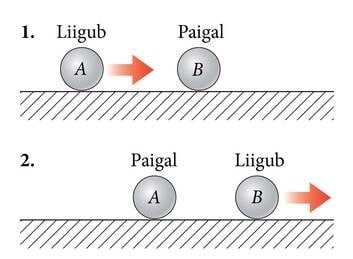
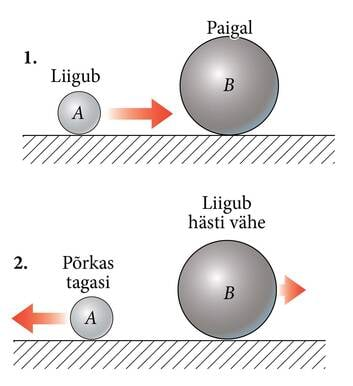
Veeretame nüüd paigalseisva palli pihta teise täpselt samasuguse palli. Paigalseisev pall hakkab siis liikuma ning see pall, mida tema pihta veeretati, jääb praktiliselt seisma (või hakkab aeglasemalt liikuma) – pallid mõjutavad teineteist ning mõlema palli kiirus muutub.
Kui korrata eelnevat katset nii, et paigalseisev pall on suure massiga ning tema vastu veeretatakse palju väiksema massiga pall, siis hakkab suurem pall hästi aeglaselt liikuma, kuid väike pall põrkab tagasi ja liigub praktiliselt sama kiirusega, mis tal enne põrget oli. Katsest võib järeldada, et kehade vastastikmõju tõttu muutub suurema massiga keha kiirus palju vähem ning väiksema massiga keha kiirus rohkem.
Kehadevahelise vastastikmõju kohta tasub meelde jätta järgmist.
- Kehade mõju on alati vastastikune – üks keha mõjutab teist ning teine esimest.
- Kehade vastastikmõju korral muutub suure massiga keha kiirus vähem kui väiksema massiga keha kiirus.
Siit järeldub ka, et kui põrand pidurdab palli hoogu, siis pall omakorda kiirendab põrandat. Aga kuna põranda ja selle külge kinnitatud maja mass on palli massist palju suurem, siis me märkame vaid palli kiiruse muutumist.
Füüsikalist suurust, mis iseloomustab ühe keha mõju teisele kehale, nimetatakse jõuks.
Jõudu tähistatakse tähega F ning jõu ühikuks on njuuton (lühend N). Jõu ühik on saanud oma nime Inglise teadlase Isaac Newtoni järgi, kes tegeles paljude loodusteadusi puudutavate teemadega ning sõnastas mehaanika põhiseadused, mis on tänapäeva füüsika nurgakiviks. Täpsemalt õpite Newtoni seadusi gümnaasiumis.
Jõud mõjub alati ühes kindlas suunas. Joonistel näidatakse jõu mõjumise suunda noolega. Noole algus tehakse alati sinna punkti, kuhu jõud mõjub. Jõu mõjumise punkti nimetatakse jõu rakenduspunktiks.
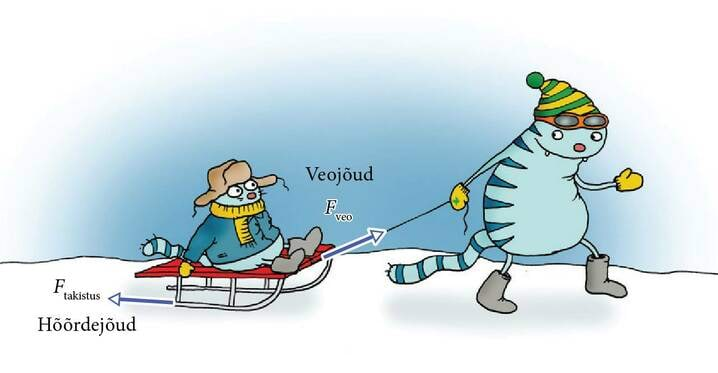
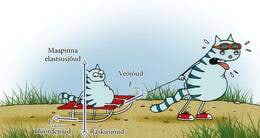
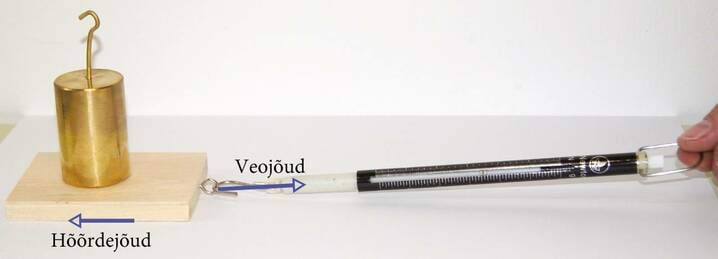
Enamasti mõjub kehale samal ajal mitu jõudu. Näiteks kelgu vedamisel mõjub kelgule veojõud, mis on kelgu tõmbamise suunaline. Samal ajal mõjub talle tee ja kelgu põhja vaheline hõõrdejõud, mis on sõidusuunale vastupidine.
Kui me tahame vaadelda seda, kuidas kehale mõjuvad jõud mõjutavad keha liikumist, on meil vaja leida kehale mõjuv summaarne jõud ehk resultantjõud. Kõrvalolevas näites saame leida resultantjõu, kui me lahutame veojõust hõõrdejõu. Me peame jõudusid lahutama, kuna need jõud on vastassuunalised:
Kelgu liikumissuunalise resultantjõu leidmisel pole vaja arvestada raskusjõu ning maapinna elastsusjõuga, kuna need jõud on veo- ja takistusjõuga risti.
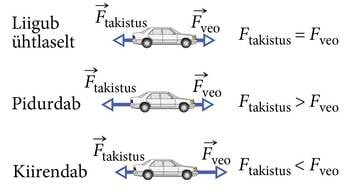
Uurime joonisel kujutatud autole mõjuvaid jõudusid. Kui veojõud on takistusjõust suurem, liigub auto kiirenevalt. Kui aga takistusjõud on suurem veojõust, liigub auto aeglustavalt.
Millal liigub joonisel kujutatud auto ühtlaselt? Me juba teame, et kui kehale ei mõju ühtegi jõudu, siis on keha paigal või liigub ühtlaselt ja sirgjooneliselt. Selgub, et sama kehtib ka siis, kui kehale mõjuvate jõudude summa on 0 (resultantjõud on 0 N).
Keha on paigal või liigub ühtlaselt ja sirgjooneliselt, kui sellele mõjuvad jõud tasakaalustavad üksteist.
Seega liigub joonisel kujutatud auto ühtlaselt siis, kui veojõud ja takistusjõud on võrdsed.
Keha liikumise muutumine
Keha kiirus või suund võib muutuda ainult siis, kui seda mõjutavad teised kehad.
Kehade vastastikmõju
Kehade mõju on alati vastastikune – üks keha mõjutab teist ning teine esimest. Kehade vastastikmõju korral muutub suure massiga keha kiirus vähem kui väiksema massiga keha kiirus.
Summaarne jõud ehk resultantjõud
Kui tahame teada, kuidas kehale mõjuvad jõud muudavad keha liikumist, peame leidma kehale mõjuva summaarse jõu ehk resultantjõu. Kui kehale mõjuvad jõud on vastassuunalised, tuleb need resultantjõu leidmisel üksteisest lahutada. Keha on paigal või liigub ühtlaselt ja sirgjooneliselt, kui sellele mõjuvad jõud tasakaalustavad üksteist.
Ilma kehadevahelise vastastikmõjuta liiguks kõik kehad ühtlaselt ja sirgjooneliselt või seisaks paigal. Miks siis kukub üles visatud pall tagasi maapinnale, ehkki ei ole mingit nähtavat takistust, miks see ei võiks jäädagi ülespoole liikuma? Miks Kuu tiirleb ümber Maa, kui hõlpsam oleks liikuda otse nagu nööri otsa seotud kivi, mida on keerutatud ja siis lahti lastud?
Looduses esineb kehadevaheline vastastikmõju, mida nimetatakse gravitatsiooniks ehk gravitatsiooniliseks vastastikmõjuks. Gravitatsioonilises vastastikmõjus olevate kehade vahel mõjub tõmbejõud, mida nimetatakse gravitatsioonijõuks.
Gravitatsioonijõud mõjub kõikidele vastastikmõjus olevatele kehadele ühtemoodi ja see on suunatud kehade keskpunktide poole.
Miks siis üles visatud pall tagasi maapinnale kukub?
Maa ja palli vahel mõjub gravitatsioonijõud. Kui pall kaalub 100 grammi, siis on gravitatsioonijõu suuruseks ligikaudu 1 N. Selline jõud mõjub nii pallile kui ka Maale, nii et rangelt võttes peaksid pall ja Maa hakkama teineteisele vastu liikuma. Kuna aga Maa mass on palli massist väga palju suurem, nihkub ta sellises vastastikmõjus väga vähe. See-eest palli mõjutab gravitatsioonijõud märgatavalt – see „kukub alla“.
Gravitatsioon esineb kõigi kehade vahel, isegi kahe pinginaabri vahel ning pinalis olevate pliiatsite vahel. Kui me seda ei tunne, siis sellepärast, et näiteks kahe pinginaabri vaheline gravitatsioonijõud on kõigest 0,0000001 N. Millest sõltub gravitatsioonijõu suurus?
Gravitatsioonijõu suurus sõltub kehade massist – mida suurem on kehade mass, seda suurem on gravitatsioonijõud.
Kui üks pinginaabritest kaaluks miljon tonni, siis oleks täpsete mõõteriistadega võimalik pinginaabrite vahel tekkiv gravitatsioonijõud ka ära mõõta. Lisaks kehade massile sõltub gravitatsioonijõu suurus ka kehade omavahelisest kaugusest. Mida kaugemal on kehad üksteisest, seda väiksem on gravitatsioonijõud. Näiteks kui inimesele mõjub maapinnal gravitatsioonijõud 800 N, siis 10 000 km kaugusel maapinnast on gravitatsioonijõud kõigest 120 N (vt tabel).
Maa või mõne teise taevakeha lähedal asuvatele kehadele mõjuvat gravitatsioonijõudu nimetatakse ka raskusjõuks. Maapinna lähedal olevatele kehadele mõjuvat raskusjõudu saab arvutada valemiga:
Selles valemis tegur g näitab, millise jõuga mõjutab Maa (või mõni muu taevakeha) tema pinnal asetsevat 1 kg keha. Tegurit g nimetatakse raskuskiirenduseks, selle ligikaudne väärtus maapinnal on g = 9,8 N/kg.Raskusjõu valem Fr = mg on igapäevaelus väga oluline, kuna annab mõtte sõnadele kaal ja kaalumine. Kaal mõõdab temale asetatud keha poolt talle avaldatavat raskusjõudu. Keha mass m on selle raskusjõuga võrdeline ja selle saab arvutada valemist m = Fr/g, kui me teame raskusjõudu Fr ja raskuskiirendust g.
Keha mass on konstantne suurus, aga keha kaal võib väga suurtes piirides muutuda, sest raskuskiirenduse g väärtus ei ole alati ja igal pool ühesugune.
Näiteks on raskuskiirenduse väärtus ekvaatoril natuke väiksem kui poolustel ning ühte ja sama keha ekvaatoril ja poolusel kaaludes saame erineva tulemuse. See erinevus on suhteliselt väike, aga kaubanduses peab sellega arvestama – banaanilasti kaal põhja poole sõites pisut kasvab.
Kuna gravitatsioonijõud sõltub kehadevahelisest kaugusest, siis sõltub raskuskiirenduse g väärtus ka kaugusest maapinnast.
Kuna raskuskiirenduse väärtus sõltub taevakehade massist, siis on erinevate planeetide läheduses raskuskiirenduse väärtus erinev ja järelikult on seal teistsugune ka kehade kaal. Näiteks Kuu pinnal on g väärtuseks 1,6 N/kg, mistõttu on Kuul mõjuv gravitatsioonijõud ja kehade kaal umbes kuus korda väiksem kui Maal. Tõstes Maal keha, mille mass on 50 kg, mõjub talle gravitatsioonijõud 500 N. Kuul tuleb aga rakendada sama palju jõudu, et tõsta keha, mille mass on suurem kui 300 kg.
Gravitatsioonijõud ja raskusjõud
Gravitatsioonilises vastastikmõjus olevate kehade vahel mõjub tõmbejõud, mida nimetatakse gravitatsioonijõuks. Mida suurem on kehade mass, seda suurem on gravitatsioonijõud. Mida kaugemal on kehad üksteisest, seda väiksem on gravitatsioonijõud. Maa lähedal mõjuvat gravitatsioonijõudu me nimetame raskusjõuks.
Päikesesüsteem tekkis ligikaudu 4,6 miljardit aastat tagasi.
Algselt oli Päikesesüsteem suur gaasipilv, mis gravitatsiooni mõjul järjest kokku tõmbus. Umbes 50 miljoni aasta jooksul muutusid rõhk ja temperatuur gaasipilve keskele tekkinud prototähe keskmes piisavalt suureks termotuumareaktsioonide käivitumiseks ning tekkis Päike.
Esialgses gaasipilves polnud aine ühtlaselt jaotunud. Kokkutõmbuv gaasipilv hakkas järjest kiiremini pöörlema ning umbes kümnendik esialgse pilve ainest paiskus väljapoole. Väljapaiskunud aine venis pöörlemise tõttu lapikuks ning moodustas lapiku protoplanetaarse pilve – ketta, milles hakkasid tekkima Päikesesüsteemi planeedid ja muud taevakehad. Teadlased arvavad, et praegu Marsi ja Jupiteri vahel asuv asteroidide vöö on nende Päikesesüsteemi algaegade jäänus, mis valdavalt Jupiteri gravitatsioonilise mõju tõttu ei ole saanud suuremaks objektiks kokku koonduda.
Algselt tekkisid kõikidel planeetidel kivimitest koosnevad tuumad, mille ümber oli ulatuslik vesiniku ja heeliumi kiht. Päikese kiirguse tugevnedes Päikesele lähemal olevate nn Maa tüüpi planeetide ümbert (Merkuur, Veenus, Maa, Marss) gaasipilv hajus. Päikesest kaugel olevad hiidplaneedid (Jupiter, Saturn, Uraan ja Neptuun) on säilitanud oma tiheda atmosfääri praeguseni.
| Protoplanetaarne ketas raadioteleskoobis. HL Tauri on noor täht Sõnni tähtkujus ja asub Maast 450 valgusaasta kaugusel. Palja silmaga vaatlemiseks on see objekt liiga nõrk, valguse nähtavas piirkonnas näeb see ala ka hoopis teistsugune välja. | Planeedid tekivad universumis ka praegu. Selle pildil on kunstnik kujutanud planeetide teket väga noore tähe Beta Pictoris ümber. Pilt on joonistatud vaatlusandmete põhjal. Arvatakse, et selle tähe ümber tekkivatel planeetidel on palju süsinikku ja need võiks olla sobilikud elu tekkeks. |
Päikesesüsteemi planeetide ümber tiirleb teadaolevalt 219 kaaslast. Suurem osa neist paikneb hiidplaneetide ümber – praeguseks on Jupiteril leitud 79 ja Saturnil 82 kaaslast. Maa-tüüpi planeetide ümber tiirleb vaid kolm kuud (Maa kaaslane Kuu ning kaks Marsi kaaslast – Phobos ja Deimos).
Päikesesüsteemi äärealadele jäävad veel kääbusplaneedid. Tuntuim neist on Pluuto – kuni 2006. aastani loeti see veel planeediks. Kuid kääbusplaneet on ka Marsi ja Jupiteri vahel tiirlev suurim asteroid Ceres.
Mõnikord on taevas näha ka komeete ehk sabatähti. Komeedid koosnevad peamiselt jääst ning külmunud gaasidest ja vähemal hulgal tolmuosakestest ning väikestest kivikestest. Päikesest kaugel on suurimate komeetide tuumade läbimõõt mõnikümmend kilomeetrit, enamiku komeetide tuuma läbimõõt on mõni kilomeeter. Päikesele lähenedes hakkab komeet soojenema. Komeedi pinnas olevad gaasid aurustuvad ning eemalduvad komeedi tuumast, moodustades kuni 200 000 km läbimõõduga komeedi pea.
Päikesetuul puhub gaasid komeedi juurest minema ning moodustub komeedi gaasiline ioonsaba (Halley komeedi pildil sinine). Saba pikkus võib olla kuni 100 miljonit kilomeetrit. Komeedi ioonsaba on alati suunatud Päikesest eemale – Päikesele läheneb komeet pea ees ning eemaldub saba ees. Komeetidel on alati ka teine saba, mida nimetatakse tolmusabaks. See tekib komeedi aurustumisel vabanenud tolmuosakestest ja jääb komeedist maha piki komeedi orbiiti. Kuna orbiidid on alati ümber Päikese, siis võivad komeedi tolmu- ja ioonsaba osutada väga erinevatesse suundadesse.
Mõned komeedid liiguvad Päikese ümber väljavenitatud ovaalset orbiiti mööda. Sellised komeedid satuvad Maa lähedale mõne või mõnesaja aasta tagant. Näiteks Halley komeet möödub maast iga 70 aasta järel. Enamik komeete on aga tähtedevahelised hulkurid, mis on pärit Päikesesüsteemi kaugetest äärealadest ja peale esimest lähenemist Päikesele lahkuvad Päikesesüsteemist igaveseks. Heledamaid komeete on võimalik jälgida ka palja silmaga, kuid neid satub Päikese lähedale harva – umbes iga 10 aasta tagant üks komeet.
Hõõrdumine on kehade kokkupuutepindade vahel esinev vastastikmõju, mis takistab kehade liikumist üksteise suhtes. Hõõrdumine esineb kõigi kehade vahel, mis kokku puutuvad. Hõõrdejõu mõjumise suund on keha liikumissuunaga alati vastupidine.
Mõnikord on hõõrdumine kasulik, näiteks siis, kui tahame jalgadega tee pealt hoogu tõugata ning liikuda. Mõningates kohtades on vaja jälle hõõrdumist vähendada – jalgrattaga on palju lihtsam sõita siis, kui rattalaagrid on õlitatud ning hõõrdumine on väga väike, kelk aga libiseb palju paremini siis, kui lumi on maas ja tee jäine.
Hõõrdumist iseloomustab hõõrdejõud – jõud, mis takistab kokkupuutes olevate kehade liikumist teineteise suhtes.
Hõõrdejõudu saab mõõta dünamomeetriga. Selleks tuleb keha külge kinnitada dünamomeeter ning vedada seda dünamomeetrist tõmmates ühtlaselt ning paralleelselt laua pinnaga. Dünamomeeter näitab siis jõudu, millega keha veetakse (veojõudu) – see on ühtlase liikumise korral võrdne hõõrdejõuga keha ja pinna vahel.
Hõõrdumise tekkimiseks on erinevaid põhjuseid, üheks peamiseks on see, et kehade pinnad ei ole siledad. Kui vaadelda luubiga raamatu pinda, võib seal märgata väikeseid konarusi. Raamatu kaane konarused jäävad laua konaruste taha kinni – see takistabki raamatu liikumist ning põhjustab hõõrdumist. Nii et üldiselt on hõõrdumine seda väiksem, mida siledamad on pinnad, ja hõõrdumine väheneb, kui panna libisevate pindade vahele õli või muud vedelikku, kuna õli täidab suuremad konarused.
Hõõrdejõud sõltub materjalidest, mis omavahel kokku puutuvad, samuti rõhumisjõust – mida suurema jõuga on hõõrduvad pinnad kokku surutud, seda suurem on hõõrdejõud. Hõõrdejõud sõltub ka sellest, kuidas kehad üksteise suhtes liiguvad. Paigalseisvat kappi on palju raskem liikuma lükata kui juba liikuvat kappi liikumas hoida.
Hõõrdejõudu, mis takistab kehade liikuma hakkamist, nimetatakse seisuhõõrdejõuks. Hõõrdejõudu, mis tekib keha libisemisel teise keha pinnal, nimetatakse liugehõõrdejõuks.
Kehade vahel tekkiv hõõrdejõud on vahel hea, vahel ebasoovitav. Näiteks autode pidurisüsteemides on hõõrdejõud kindlasti soovitav.
| Hõõrdudes kehad soojenevad, äärmuslikes oludes võivad nad lausa hõõguma hakata. Vasakpoolsel pildil hõõguvadki võidusõiduauto esimeste rataste pidurikettad punaselt. | Auto pidurisüsteem. Ratta külge on kinnitatud ketas (piduriketas), mis on servapidi pilus. Pidurdades surutakse vastu piduriketast piduriklotsid, tekib tugev hõõrdumine. |
Paljudel juhtudel üritatakse hõõrdumist igati vähendada. Õli ja teiste määrdeainete kasutamist me juba mainisime – ilma õlita automootor kuumeneb hõõrdumise tõttu väga kiiresti ning kuumade detailide paisumise pärast n-ö jookseb kokku. Aga meenutada tasub ka näiteks suuskade määrimise keerukat tööd.
Lisaks libisemisele võivad kehad ka veereda. Ehkki kehade veeremist takistav jõud on mitu korda väiksem kui liugehõõrdejõud, on see siiski olemas ja seda nimetatakse veerehõõrdejõuks.
Hõõrdumine ja hõõrdejõud
Hõõrdumine on kehade kokkupuutepindade vahel esinev vastastikmõju, mis takistab kehade liikumist üksteise suhtes. Hõõrdumist iseloomustab hõõrdejõud – jõud, mis takistab kokkupuutes olevate kehade liikumist teineteise suhtes.
Seisuhõõrdejõud ja liugehõõrdejõud
Hõõrdejõudu, mis takistab kehade liikuma hakkamist, nimetatakse seisuhõõrdejõuks. Hõõrdejõudu, mis tekib keha libisemisel teise keha pinnal, nimetatakse liugehõõrdejõuks.
Ehkki kehade veeremist takistav jõud on mitu korda väiksem kui liugehõõrdejõud, on see siiski olemas ja seda nimetatakse veerehõõrdejõuks.
Kõik kehad muudavad vähemal või suuremal määral oma kuju, kui neid jõuga mõjutada. Sellist keha kuju muutumist nimetatakse deformatsiooniks. Näiteks kui istud toolile, siis tool deformeerub, samuti deformeerub laud, kui asetad sellele raamatu, ning raamat deformeerub ükskõik, kuhu sa selle toetad. Me lihtsalt ei märka neid deformatsioone, kuna need on väga väikesed. Samas paljudel juhtudel on kehade deformatsioon vägagi märgatav. Kuidas deformatsiooni kirjeldada?
Kehasid, mis taastavad oma kuju pärast deformeeriva jõu lõppemist, nimetatakse elastseteks. Kummist ja terasest valmistatud kehad on enamasti elastsed. Kehasid, mis säilitavad oma kuju pärast deformeeriva jõu lõppemist, nimetatakse plastseteks ehk plastilisteks kehadeks. Näiteks plastiliinist valmistatud kehad on plastsed, sama võib öelda leivale määritava või kohta.
Sarnaselt öeldakse, et deformatsioon on elastne, kui deformeeriva jõu lõppemisel keha taastab oma esialgse kuju. Deformatsioon on plastiline, kui deformeeriva jõu lõppemisel keha oma esialgset kuju ei taasta.
Kuju muutmiseks on vaja rakendada jõudu. Keha ise aga takistab oma kuju muutumist. Kehas selle deformeerimisel tekkivat jõudu nimetatakse elastsusjõuks. Elastsusjõud on vastassuunaline keha deformeeriva jõuga.
Elastsete kehade korral kirjeldab kehas tekkivat elastsusjõudu Hooke’i seadus: kehas tekkiv elastsusjõud on võrdeline keha pikenemisega.
Üks ja sama keha võib olla nii elastne kui ka plastiline. Venitades dünamomeetri vedru väikese jõuga, st natuke, taastab ta pärast deformatsiooni oma kuju ja me saame seda uuesti kasutada. Venitades aga vedru suure jõuga – tõmmates vedru sirgeks –, ei taasta vedru endist kuju, vaid jääbki väljavenitatuks. Midagi sarnast toimub ka näiteks joonlauaga, mida saab natuke painutada, aga rohkem painutades läheb see lõpuks katki.
Näidisülesanne
Määra katseliselt tundmatu keha mass. Kasutada on järgmised katsevahendid: tundmatu keha, 100grammine keha, mõõtejoonlaud, kumminiit.
Lahendus
Kumminiiti saame kasutada dünamomeetrina. Kinnitame 100grammise keha kumminiidi külge. Mõõdame kumminiidi pikkuse enne kummi välja venitamist.Mõõdame kumminiidi pikkuse , kui 100grammine keha ripub kumminiidi küljes. Lahutades viimasest kumminiidi esialgse pikkuse , saame teada, kuipalju kumminiit pikenes
Kui keha ripub kumminiidi küljes, siis on elastsusjõud kumminiidis võrdnekeha raskusjõuga. Kumminiidi pikenemine on võrdeline kumminiidis tekkiva elastsusjõuga ning kumminiidi külge kinnitatud keha raskusjõuga.
Teades, et 100grammisele kehale mõjuv raskusjõud on
saame leida ka kumminiiti iseloomustava jäikusteguri väärtuse:
Riputame nüüd sama pika kumminiidi külge tundmatu keha ning mõõdame kumminiidi pikkuse . Tundmatu keha korral venis kumminiit seega
Teades kumminiidi jäikustegurit , saame leida tundmatule kehale mõjuva raskusjõu .
Sellele valemile saab anda ka üldise kuju, kui asendame tuntud keha massi -ga
Vastus: Katses tuleks mõõta kumminiidi pikenemine, kui selle külge on riputatud tuntud ja tundmatu keha. Pärast seda tuleks kasutada arvutuskäigus leitud valemit.
Pehmet saia on kõige parem lõigata hästi terava noaga. Lõigates saia nüri noaga, vajub sai lihtsalt kokku ning lõikamisest ei tule midagi välja. Mida füüsika selle kohta ütleb?
Terava ja nüri noaga lõikamise erinevus seisneb selles, et nugade kokkupuutepindala saiaga on erinev ning lõikekohas avaldatakse saiale küll sarnast jõudu, aga väga erinevat rõhku.
Rõhk iseloomustab rõhumisjõu mõju pinnale. Rõhk arvutatakse jagades rõhumisjõu pindalaga, millele jõud mõjub.
Rõhku tähistatakse tähega p, jõudu tähega F ning kokkupuutepindala tähega S. Seega saame avaldada rõhu valemina
Rõhu ühik on paskal (lühend Pa). Rõhk üks paskal näitab seda, et ühele ruutmeetrisele pinnale rõhub jõud üks njuuton:
Terava noaga lõigates on noa ja saia kokkupuutepindala hästi väike ning lõikekohas saiale avaldatav rõhk on seega palju suurem kui nüri noaga lõigates.
Samamoodi tuleb rõhuga arvestada ka põllutöömasinate ehitamisel. Traktoritel on enamasti suured ja laiad rehvid just seetõttu, et traktori rõhk maapinnale oleks võimalikult väike. Mida väiksema rõhuga traktor maapinda mõjutab, seda vähem vajub traktor pehmesse pinnasesse ning vajutab seda vähem kokku.
Kui autos ei ole turvapatja, lendab autojuht autode kokkupõrkel vastu rooli (nüüd me juba teame, et selles avaldub keha inertsus). Kuna inimese ja rooli vaheline kokkupuutepindala on väike, mõjub seal inimesele suur rõhk – seetõttu võivad näiteks roided murduda.
Kui autos on turvapadi, siis lendab inimene avarii korral vastu turvapatja. Kuna turvapadja ja inimese vaheline kokkupuutepindala on palju suurem, siis mõjub inimesele palju väiksem rõhk ning vigastused, mis võivad tekkida, on samuti palju väiksemad.
Näiteid rõhu hindamise kasulikkusest on lõputult. Terav või nüri naaskel, lumeräätsad, tikk-kontsad ...
Näidisülesanne
Mitu korda suuremat rõhku avaldab kaaluv õpilane põrandale, kui ta tooliga kiigub võrreldes sellega, kui ta toolil istub? Neljal jalal seistes on tooli ühe jala ja põranda kokkupuutepindala . Kiikudes on tooli ühe jala ja põranda kokkupuute pindala umbes . Tooli massi võib antud ülesandes jätta arvestamata.
Lahendus
Kui õpilane istub toolil, mõjutab tool põrandat nelja jalaga, seega kogu kokkupuutepindala on S1=4⋅3cm2=12cm2. Kiikudes toetab tool põrandat kahe jalaga, seega kokkupuutepindala on S2=2⋅0,1cm2=0,2cm2.
Andmed
m=50kg
S1=4⋅3cm2=12cm2=0,0012m2
S2=2⋅0,1cm2=0,2cm2=0,00002m2––––––––––––––––––––––––––––––––––––––––––––
p1−?
p2−?
Arvutused:
p1=FS1=4900,0012=408333Pa=408kPa
p2=FS2=4900,00002=24500000Pa=24500kPa
k=p2p1=24500408=60korda––––––––––––––––––
Vastus. Tooliga kiikudes avaldab õpilane põrandale korda suuremat rõhku kui rahulikult toolil istudes.
Tahketes kehades mõjub rõhk ainult ühes kindlas suunas. Nuga mõjutab saia peamiselt vajutamise suunas. Kui toolil istuda, mõjutab tool põrandat raskusjõu mõju suunas. Vedelikes ja gaasides mõjub rõhk teistmoodi. Kuidas?
Võtame õõnsa kera, milles on palju väikseid avasid, ja avaldame keraga ühendatud silindri kaudu keras olevale vedelikule rõhku. Rõhu mõjul purskab vedelik välja ka rõhu mõju suunaga vastupidistes suundades, joonisel otse üles. Sarnaseid katseid võib välja mõelda veelgi:
Selliste katsete põhjal saab sõnastada üldise seaduse, mida tuntakse Pascali seaduse nime all.
Vedelikule või gaasile avaldatud rõhk levib vedelikes ja gaasides igas suunas ühtemoodi.
Rõhu levimist vedelikes ja gaasides uuris Blaise Pascal (1623–1662), kes oli Prantsuse matemaatik, füüsik ja filosoof. Teda peetakse üheks hüdrostaatika (teadusharu, mis uurib tasakaalus olevat vedelikku) rajajaks. Oma eksperimentide tulemusena sõnastas ta seaduse, mida tuntakse kui Pascali seadust, mille kohaselt kandub rõhk vedelikes ja gaasides edasi igas suunas ühtlaselt. Pascal oli ka üks esimesi, kes arvutas välja atmosfääri ligikaudse massi.
Pascal ei piirdunud ainult teoreetiliste uurimistega. Selleks, et abistada oma matemaatikust isa arvutuste juures, leiutas ta mehaanilise arvutusmasina, milles oli kaheksa liikuvat ketast. Selle abil oli võimalik arvutada kuni 8kohalisi summasid.
Pascali seaduse rakendusi me kohtame igapäevaelus väga tihti. See on ju tegelikult väga mugav – kui avaldad vooliku ühes otsas selle sees olevale vedelikule rõhku, siis vooliku teises otsas mõjub seesama rõhk millelegi, mida on vaja liigutada. Ja seda jõudu on võimalik lihtsalt jagada, kui lisada voolikule üks või mitu haru. Kastmissüsteemid, autode pidurisüsteemid, linnade ja majade veevärk ... seda nimekirja võiks jätkata pikalt.
| Sõiduauto piduripumba ehitus. Õli surutakse kahte voolikusse, üks läheb esimeste, teine tagumiste rataste juurde. Autodes kasutatavad hüdraulikaseadmed on tihti ootamatult nutikad. See pump näiteks surub õli vedelikuringi 1 ka siis, kui vedelikuringi 2 voolik läbi lõigata. Ja vastupidi. Kas oskad näha, kuidas see võimalik on? | Väliselt näeb piduripump välja niisugune. |
Olgu meil kolm ühesugust klaasi, üks on täidetud liiva, teine vee ja kolmas vatiga. Milline neist klaasidest on kõige raskem?
Oma kogemuse põhjal oskame kohe öelda, et kõige raskem on liivaga täidetud klaas ning kõige kergem vatiga täidetud klaas. Oleme sellega tihti kokku puutunud, et ühesuguse ruumalaga kehade massid on erinevad. Ütleme selle kohta, et liiv on kõige suurema tihedusega ning vatt kõige väiksema tihedusega.
Aine tihedus on füüsikaline suurus, mis näitab, kui suur on ühe ruumalaühiku aine mass.
Teame ka, et aine tiheduse definitsiooni saab kirja panna kujul:
Tiheduse ühik on massiühik jagatud ruumalaühikuga. Sagedamini kasutatavad ühikud on g/cm3, kg/dm3 ja kg/m3.
Meile kõige olulisem aine on vesi ning selle tihedust võikski peast teada. Vee ligikaudne tihedus väljendatuna erinevates ühikutes on
ρvesi = 1 g/cm3 = 1 kg/dm3 = 1000 kg/m3
Nende kehade puhul, mis koosnevad mitmest ainest, saame leida keha keskmise tiheduse. Keha keskmise tiheduse leidmiseks jagame keha kogu massi keha kogu ruumalaga. Suured laevad seisavad samuti vee peal, sest laevas on palju ruumi, mida täidab ainult õhk, ning laeva keskmine tihedus on vee tihedusest palju väiksem.
Aine tiheduse teadmine on oluline erinevate masinate ehitamisel. Näiteks peavad olema lennukid tehtud väikese tihedusega kergest materjalist, et lennuki mass oleks võimalikult väike. Enamasti kasutatakse lennukite ehitamisel alumiiniumi sulameid, kuna need on tugevad, kuid võrreldes rauaga kolm korda väiksema tihedusega.
Tihti on meil vaja teisendada tiheduse ühikuid ühest mõõtühikust teise. Teades vee tihedust erinevates ühikutes, on kerge teisendada ka kõigi teiste ainete tihedusi. Näiteks alumiiniumi tihedus on 2700 kg/m3. Meil on vaja seda väljendada ühikutes g/cm3. Teades, et vee tihedus on 1000 kg/m3 = 1 g/cm3, saab öelda, et alumiiniumi tihedus on 2700 kg/m3 = 2,7 kg/dm3 = 2,7 g/cm3. Vee tiheduse ühikutest näeme, et ühikud kg/m3 ning g/cm3 erinevad teineteisest 1000 korda, seega erinevad ka alumiiniumi tiheduse ühikud 1000 korda.
Kui meil on aga vaja väljendada alumiiniumi tihedus mõnes teises ühikus, näiteks g/dm3, peame teisendama eraldi massiühiku ja ruumalaühiku.
1 kg = 1000 g
1 m3 = 1000 dm3
Teisendades saame
Tuletame ka meelde, et ainete tihedus sõltub temperatuurist. Kõige rohkem mõjutab temperatuur gaaside tihedust. Vedelike ja tahkete ainete tihedus muutub temperatuuri tõustes või langedes vähe. Vee täpne tihedus 4 ˚C juures on 0,997 g/cm3, kuid tabelis on antud ümardatud tihedus (1,0 g/cm3).
Tahkete ainete tihedused 20°juuresVedelike tihedused 25°juuresGaaside tihedused 0°juuresAine tihedus
Aine tihedus on füüsikaline suurus, mis näitab, kui suur on ühe ruumalaühiku aine mass. Selle definitsiooni saab kirja panna kujul
Tiheduse ühikuks on kg/m3. Nende kehade puhul, mis koosnevad mitmest ainest, saame leida keha keskmise tiheduse.
Kui suurt rõhku peaksime taluma sügaval vee all? Et seda teada saada, lahendame lihtsama ülesande ja uurime, millist rõhku avaldab vesi anuma põhjale. Teeme seda nii, nagu füüsikas kombeks – kasutame olemasolevaid üldiseid teadmisi uute teadmiste tuletamiseks.
Olgu silindrilise anuma põhjapindala S ning selles oleva vedelikusamba kõrgus h. Anumas oleva vee ruumala on seega:
Vee massi saame leida vee tiheduse kaudu:
Teades vee massi, saame leida raskusjõu, mida vesi avaldab anuma põhjale:
Kasutades rõhu definitsioonivalemit, arvutame vee rõhu anuma põhjale:
ehk
Kokkuvõttes võime öelda, et vedelikusamba rõhk on võrdne vedelikusamba kõrguse, vedeliku tiheduse ja raskuskiirenduse g korrutisega. Tulemusest näeme ka, et rõhk anuma põhjale ei sõltu vedelikusamba mõõtmetest (anuma põhja pindalast) – ehkki me ülesande lahendamist alustades arvestasime põhja pindalaga, siis lahenduse käigus see taandus valemitest välja.
Detailsemad arvutused näitavad, et rõhk anuma põhjale ei sõltu ka anuma kujust. Veendume selles katseliselt, vaadeldes vedelikku erineva kujuga ühendatud torudes (vt pilt allpool). Katses näeme, et vedeliku tase kõigis torudes on ühesugune, ehkki torude kuju, seega ka vedeliku kogus torudes on erinev. Selline olukord on võimalik vaid juhul, kui rõhk on ühesugune kõikide torude ühenduskohtades alumise horisontaalse toru külge. Tõepoolest, kui rõhud oleksid erinevad, hakkaks vedelik voolama väiksema rõhuga torusse.
Näidisülesanne
Kui suurt rõhku avaldab silindrilises klaasis olev vesi klaasi põhjale, kui klaas on ääreni vett täis? Klaasi põhjapindala on .
Lahendus
Vedeliku poolt avaldatud rõhu leidmiseks peame teadma vedeliku tihedust ning vedelikusamba kõrgust. Kuna me teame, et klaasi ruumala on ning põhjapindala , saame leida, kui kõrgele vedelik klaasi põhjast ulatub.
Andmed
V=200cm3
S=25cm2
ρ=1,0g/cm3=1000kg/m3–––––––––––––––––––––––––––––––
p−?
Arvutused:
p=1000kg/m3⋅9,8N/kg⋅0,08m≈780Pa––––––––––––––
Vastus. Vedelik avaldab klaasi põhjale rõhku 780Pa.
Manomeeter on seade, millega saab mõõta vedeliku või gaasi poolt anuma seintele avaldatavat rõhku. Pascali seaduse järgi on see ühtlasi rõhk vedeliku või gaasi sees. Üheks lihtsamaks manomeetriks, mida saab ise ehitada, on U-toru manomeeter. Kuidas see töötab?
Uurime veega täidetud U-kujulist toru (U-toru), mis on osaliselt täidetud veega ja mille üks ots on kummivoolikuga ühendatud kinnise anumaga, kus oleva gaasi rõhku me mõõta tahame. Vedeliku sambad U-toru haarades on erinevatel kõrgustel, järelikult erineb rõhk anumas atmosfäärirõhust. Aga kui palju?
Rõhk ühendatud anumates on igal kõrgusel ühesugune, sest muidu hakkaks vedelik anumas voolama kõrgema rõhuga piirkonnast madalama rõhuga piirkonda. Seega on rõhk õhu ja vee piiril haaras B samasugune kui rõhk vees sellel kõrgusel haaras A. Järelikult on uuritavas anumas rõhk parajasti sama palju atmosfäärirõhust suurem, kui palju avaldab rõhku Δh kõrgune vedelikusammas. Nii et saame kirjutada:
ja
Tulemusest näeme, et kui mõõdame selliselt ühendatud U-torus ära Δh ja teame atmosfäärirõhku patm, siis saame leitud valemi abil arvutada rõhu anumas px. Näeme ka, et U-toruga saab mõõta rõhu erinevust atmosfäärirõhust, st tulemuse saamiseks peame teadma atmosfäärirõhku patm.
U-toru on osaliselt täidetud veega. U-toru ühte harusse kallatakse kõrgune toiduõli kiht. Kui palju muutub veetase teises toru harus võrreldes veetasemega enne toiduõli lisamist? Vee tihedus on ning toiduõli tihedus .
Lahendus
Joonistame kujutletava sirge õli ja vee piirpinnalt horisontaalselt U-toru teisele haarale. Selliselt eraldame ainult veega täidetud U-toru harus osa vedelikusambast. Rõhk samal sügavusel vees on ühendatud anumates igal pool sama. Seega on rõhk kujutletava sirgega määratud kõrgusel mõlemas U-toru harus ühesugune. Ja rõhk, mida avaldab toiduõli sellel kõrgusel, on sama suur kui rõhk, mida avaldab vesi U-toru teises harus samal kõrgusel.
Andmed
ρvesi=1,0g/cm3=1000kg/m3
ρ˜oli=0,9g/cm3=900kg/m3
h˜oli=2cm=0,02m–––––––––––––––––––––––
hvesi=?
Arvutused
p˜oli=ρ˜oligh˜oli=900kg/m3⋅9,8N/kg⋅0,02m=176,4Pa
Avaldades rõhu arvutamise valemist vedelikusamba kõrguse ja kasutades seda seost, saame:
hvesi=pvesiρvesig=176,4Pa1000kg/m3⋅9,8N/kg=0,018m=1,8cm
Niisiis, veetase ühes torus on 1,8cm kõrgemal kui veetase (vee ja toiduõli piirpind) teises harus. Ilma toiduõlita oleksid veetasemed samal kõrgusel ehk siis 0,9cm allpool.
Vastus. Veetase tõuseb toiduõli lisades 0,9cm võrra.
Tehnoloogias ja teaduses on vaja vedelikus või gaasis olevat rõhku päris tihti mõõta – autoga sõites me kontrollime pidevalt rõhku mootori õlisüsteemis, lennukis kontrollitakse rõhku salongis, edaspidi räägime ka õhurõhu mõõtmisest. Nii on olemas ka väga erinevaid manomeetreid.
Üheks lihtsamaks metallmanomeetriks on suletud otsaga poolkaarekujuline toru. Kui sellises torus rõhk kasvab, siis hakkab toru sirgemaks painduma samamoodi, nagu tühja piklikku õhupalli õhku puhudes ajab see ennast sirgu. Elastsusjõud aga takistab toru paindumist. Mida suurem on torus olev rõhk, seda rohkem toru paindub, toru külge on kinnitatud osuti ja skaalalt on võimalik rõhk välja lugeda.
Maa atmosfääri poolt avaldatavat rõhku nimetatakse õhurõhuks. Õhurõhku me ise ei taju, kuna see mõjutab meid kogu aeg ning me oleme sellega harjunud. Aga me tajume õhurõhu kiiret muutumist – lennuki maandumisel ja õhkutõusmisel, autoga mäest üles või alla sõites, isegi kiires liftis lähevad meie kõrvad lukku. Kuidas õhurõhk tekib ja miks on ta erinevatel kõrgustel erinev?
Atmosfääris tekkivast õhurõhust saab mõelda sarnaselt sellega, nagu tegime vedelikusamba poolt anuma põhjale avaldatavat rõhku arvutades. Kujutagem lihtsalt ette, et atmosfäär on kui üks tohutu õhuookean, mida gravitatsioonijõud õhukese kihina Maa ümber hoiab. Oma igapäevaelus jalutame selle õhuookeani põhjas. Sellisest kujutluspildist peaks meile kohe selge olema, et õhurõhk on see, kui ülemised atmosfäärikihid suruvad alumisi. Ja kuna kõrgel mägedes on õhu kiht meie kohal õhem, peab seal ka õhurõhk väiksem olema.
Siiski õhurõhku ei ole võimalik arvutada valemiga p = ρhg. Põhjuseks on see, et erinevalt vedelikest saab gaase kokku suruda ja nii on kõrgemal õhu tihedus väiksem (õhk on hõredam). Õhurõhu väärtust erinevatel kõrgustel saame teada tabelitest ja joonistelt, üks selline on ka juuresoleval pildil. Aga kuidas õhurõhku mõõta?
Õhurõhku on võimalik mõõta kaudsel teel. 1643. aastal tegi Itaalia füüsik Torricelli katse, kus ta täitis ühest otsast suletud toru elavhõbedaga ning asetas selle tagurpidi elavhõbeda anumasse. Osa elavhõbedast voolas torust välja ning torusse jäänud elavhõbeda kõrgus oli 760 mm. Torricelli kordas katset erineva kuju ning pikkusega elavhõbeda toruga, kuid torusse jäänud elavhõbeda kõrgus oli ikka 760 mm. Järelikult ei mõjuta tulemust mitte toru kuju, vaid välised tegurid – ehk siis õhurõhk. Seega saab sellist katseseadet kasutada õhurõhu mõõtmiseks.
| Nii tegi Torricelli oma katset. Elavhõbeda samba kõrgus torus sõltub vaid õhurõhust. | Kõrgel mägedes on raskem hingata. Selle põhjuseks on väiksem õhurõhk – kopsudes asuvad alveoolid, milles on respiratoorne membraan, kust kaudu toimub hapniku omastamine. Aga need membraanid ei toimi enam, kui hapniku rõhk kopsudes ei ole piisavalt suur. |
Sellest katsest pärineb ka laialdaselt kasutatav kokkuleppeline normaalrõhu suurus 760 mmHg (loe 760 millimeetrit elavhõbeda sammast). Paskalites teeb see ligikaudu 100 000 Pa (p = ρgh = 13600 · 9,8 · 0,76 = 101 292,3 Pa).
Torricelli kasutatud seadet nimetatakse elavhõbebaromeetriks – elavhõbedaga täidetud toru saab varustada skaalaga ja rõhu ühikuks on siis mmHg. Tänapäeval on elavhõbe kui tervisele kahjulik aine tavakasutuses keelatud ja õhurõhku mõõdetakse teistsugustel põhimõtetel töötavate baromeetritega.
Õhurõhu muutused põhjustavad ilma muutusi. Seetõttu on baromeetreid kasutatud ka ilma ennustamiseks. Tõepoolest, kui õhurõhk on mingis piirkonnas kõrgem kui normaalrõhk, siis on selle piirkonna kohal kõrgrõhkkond. Suvel kaasneb sellega enamasti ilus selge ilm ning võib esineda kuumalaineid. Talvel aga võib kõrgrõhkkonnaga kaasneda käre pakane. Kui õhurõhk on mingis piirkonnas normaalrõhust väiksem, siis valitseb selles piirkonnas madalrõhkkond, mis toob endaga kaasa enamasti pilvise ilma ning sademed. Suvel kaasneb sellega ilma jahenemine, kuid talvel seevastu ilma soojenemine.
Ka meie kõrv mõõdab omal moel rõhku. Et sisekõrv ei ole atmosfääriga ühenduses, siis õhurõhu muutudes tekib kahel pool trummikilet rõhkude erinevus. Sellise rõhkude erinevuse tõttu surutakse trummikilet kas sissepoole (õhurõhk suureneb) või tõmmatakse seda väljapoole (õhurõhk väheneb). Neelatamisel see tunne enamasti kaob, kuna neelamise ajal ühendatakse sisekõrv välisõhuga ning rõhud kõrvas võrdsustuvad.
Paneme tähele, et ka vee all mõjutab meid lisaks vedelikusamba rõhule ka õhurõhk – see mõjub vedeliku pinnale ning kandub siis Pascali seaduse kohaselt ka vee alla. Seega võime öelda, et rõhk vedelikes võrdub õhurõhu ja vedelikusamba rõhu summaga.
Vesi mõjutab vette asetatud keha ka sel moel, et „lükkab“ seda ülespoole. Oleme seda nähtust kindlasti tähele pannud, kui kergeid esemeid vee alla surume. Jõudu, mis lükkab vedeliku või gaasi sisse asetatud keha ülespoole, nimetatakse üleslükkejõuks. Miks see jõud tekib ja kui suur see on?
Üleslükkejõu uurimiseks riputame dünamomeetri külge metallkeha ning sukeldame selle järk-järgult vette, samal ajal dünamomeetri näitu jälgides. Katses näeme, et dünamomeeter näitab kõige suuremat jõudu siis, kui keha on õhus. Kõige väiksem jõud mõjub dünamomeetrile siis, kui keha on täielikult vee all.
Üleslükkejõu tekkimise põhjuste mõistmiseks vaatleme vette asetatud metallist kuupi küljepindalaga ning uurime, millised jõud sellele kuubile mõjuvad.
Teame, et rõhk vedelikus sõltub vaid vedelikusamba kõrgusest. Seega on paremalt ja vasakult ning eest ja tagant klotsi külgedele avalduvad rõhumisjõud võrdsed ja need jõud klotsi liigutada ei saa. Samas klotsi ülemisele ja alumisele tahule mõjuvad rõhumisjõud on erinevad – kuna alumine tahk on sügavamal vees, avaldab vesi sellele suuremat rõhku. Et ülespoole suunatud jõud on suurem kui allapoole suunatud jõud, siis on ka summaarne jõud suunatud üles. See ongi üleslükkejõud.
Kuidas üleslükkejõudu arvutada? Teame, et ülemisele tahule avaldab vesi rõhku p1=ρgh1 ning alumisele tahule rõhku p2=ρgh2. Ülemisele ja alumisele tahule mõjuva jõu saame arvutada rõhu valemist , kus on klotsi ülemise ja alumise tahu pindala:
ning
Summaarne jõud, mida vesi klotsile avaldab, on nende jõudude vahe ning see on suunatud alt üles.
Kõrguste ja vahe on klotsi kõrgus, järelikult on korrutis S(h2−h1) klotsi ruumala . Seega saame kuubile mõjuva üleslükkejõu kirja panna valemina
Seda valemit saab kasutada igasuguse kujuga kehadele mõjuva üleslükkejõu arvutamiseks. Vedelikes kehale mõjuv üleslükkejõud on arvuliselt võrdne selle vedeliku tiheduse, raskuskiirenduse ja vedelikus oleva keha ruumala korrutisega.
Tuleme nüüd tagasi katse juurde, kus osaliselt vette sukeldatud keha korral näitas dünamomeeter suuremat jõudu (ja väiksemat üleslükkejõudu) kui täielikult vette sukeldatud keha korral.
Ilmselt saab vedelik üleslükkejõudu avaldada vaid sellele osale kehast, mis on reaalselt vette sukeldatud. Kui keha on vaid osaliselt sukeldatud, siis peaks vähenema ka üleslükkejõud, ja seda kinnitab ka katse.
Kui uurime üleslükkejõu valemit, siis näeme, et selle parema poole võib kirja panna kui , kus on sellise vedeliku koguse mass, mille ruumala võrdub vedelikku sukeldatud keha ruumalaga. Sellise veekoguse kohta võime öelda, et see on keha poolt välja tõrjutud vedelik. Seega võib kehale mõjuvat üleslükkejõudu defineerida ka välja tõrjutud vedeliku hulga kaudu. Vedelikku sukeldatud kehale mõjuv üleslükkejõud on võrdne keha poolt välja tõrjutud vedelikule mõjuva raskusjõuga.
Üleslükkejõud mõjub ka gaaside korral, kuid enamasti me seda tähele ei pane, kuna gaasi tihedus on väga väike. Gaasides mõjuvat üleslükkejõudu märkame näiteks heeliumiga täidetud õhupalli korral.
Näidisülesanne
Kui suurt jõudu tuleb rakendada, et tõsta vee all olevat 104kg raskust graniidist kivi? Graniidi tihedus on 2,6g/cm3.
Lahendus
Vee all mõjub kivile raskusjõud ning vee üleslükkejõud. Üleslükkejõud on raskussuunale vastupidine, seega aitab üleslükkejõud kivi tõsta. Kivile rakendatav jõud on nende jõudude vahe.
Andmed
m=104kg
ρvesi=1000kg/m3
ρkivi=2,6g/cm3=2600kg/m3––––––––––––––––––––––––––––––––––
Ft˜oste−?
Arvutused
Vkivi=mρkivi=104kg2600kg/m3=0,04m3
Ft˜oste=Fr−F¨u=1019N−392N=627N≈630N––––––––––––
Vastus Kivi tõstmiseks vees tuleb rakendada jõudu 630N.
Vette asetatud kivi vajub põhja. Vette asetatud puutükk tõuseb pinnale isegi siis, kui seda vee alla vajutada. Kui suure puidust parve peaks ehitama, et see kivi raskuse all põhja ei vajuks?
Me juba teame, et vees olevatele kehadele mõjub kaks jõudu – keha raskusjõud, mis on suunatud alla, ning vedeliku üleslükkejõud, mis on suunatud üles. Kivi raskusjõud on vee üleslükkejõust suurem, mistõttu keha vajub põhja. Puutüki puhul on aga vee üleslükkejõud suurem kui puutükile mõjuv raskusjõud, mistõttu tõuseb puutükk pinnale.
Pöörame nüüd tähelepanu ka sellele, et pinnale tõustes jääb osa puidust veest välja. Tõepoolest, et veest välja kerkides puutükile mõjuv üleslükkejõud väheneb, siis mingil hetkel üleslükkejõud ja raskusjõud võrdsustuvad. Puutükk jääb veepinnale ujuma.
Raskusjõudu ja üleslükkejõudu võrreldes võime niisiis öelda, et keha ujub, kui kehale mõjuv üleslükkejõud on arvuliselt võrdne keha raskusjõuga ning osa kehast on veest väljas. Kui keha asub täielikult vedelikus ning üleslükkejõud ja raskusjõud on arvuliselt võrdsed, siis ütleme, keha heljub. Kui keha raskusjõud on suurem kui kehale mõjuv üleslükkejõud, siis keha upub.
Seostame nüüd ujumise ja uppumise tingimuse keha omadustega. Vaatleme massiga m ning tihedusega ρk klotsi, mis heljub vees. Klotsile mõjuv raskusjõud on . Avaldades klotsi massi tiheduse kaudu, saame:
kus V on klotsi ruumala. Klotsile mõjuv üleslükkejõud on
kus on vee tihedus. Kuna me teame, et heljumise korral on Fr=F¨u, siis saame kirjutada
Lihtsustades avaldist, saame heljumise tingimuseks
Seega sõltub keha heljumine vees keha ja vedeliku tihedusest, mitte keha mõõtmetest. Keha heljub, kui keha ja vedeliku tihedused on võrdsed. Raskusjõu ja üleslükkejõu võrdlusest saame ka järeldada, et keha ujub, kui keha tihedus on vedeliku tihedusest väiksem, ning keha upub, kui keha tihedus on vedeliku tihedusest suurem.
Kui uurime puidust klotsi ujumist vees ja õlis, siis näeme, et õlis vajub see natuke sügavamale kui vees. See on ka oodatav tulemus – õli tihedus (900 kg/m3) on vee tihedusest (1000 kg/m3) väiksem, seega mõjub õlis klotsile väiksem üleslükkejõud.
Sellest saab järeldada, et mida suurem on vedeliku tihedus võrreldes keha tihedusega, seda väiksem osa ujuvast kehast asub vedelikus. Seda asjaolu kasutatakse vedelike tiheduste mõõtmiseks areomeetriga. Areomeetri alaosas paikneb koormis ning ülaosas peenike skaalaga toru. Areomeeter asetatakse vedelikku ning selle järgi, kui sügavale areomeeter sukeldub, saab teada vedeliku tiheduse.
Näidisülesanne
Kolmeliitrise metallist kausi mass on 200 grammi. Kauss koos puuviljadega pannakse vee peale ujuma. Mitu kilogrammi puuvilju võib kausis olla, et kauss ujuks vee peal?
Lahendus
Kauss jääb vee peale ujuma, kui kausi ja puuviljade keskmine tihedus on väiksem (piirjuhul võrdne) vee tihedusega.
Andmed
mkauss=200g=0,2kg
Vkauss=3dm3=0,003m3
ρvesi=1000kg/m3––––––––––––––––––––
mpuuviljad−?
Arvutused
mkaussjapuuviljad=ρkaussjapuuviljad⋅Vkauss=1000kg/m3⋅0,003m3=3kg
mpuuviljad=mkaussjapuuviljad−mkauss=3kg−0,2kg=2,8kg––––––––––––––
Vastus. Kauss jääb vee peale ujuma, kui seal on vähem kui 2,8kg puuvilju.
Keha ujumine, ujumise ja uppumise tingimus
Raskusjõudu ja vees kehale mõjuvat üleslükkejõudu võrreldes võime öelda, et keha ujub, kui kehale mõjuv üleslükkejõud on arvuliselt võrdne keha raskusjõuga ning osa kehast on veest väljas. Kui keha asub täielikult vedelikus ning üleslükkejõud ja raskusjõud on arvuliselt võrdsed, siis ütleme, keha heljub. Kui keha raskusjõud on suurem kui kehale mõjuv üleslükkejõud, siis keha upub. Heljumise korral:
Igapäevaelus kasutame sõnu töö ja energia väga erinevates tähendustes. Räägime näiteks, et käimiseks, jooksmiseks ja mõtlemiseks kulub energiat. Töö võib olla näiteks kraavi kaevamine, rääkimine, laulmine või auto juhtimine. Aga kuidas tööd ja energiat mõõta?
Käesolevas peatükis uurime mehaanilist tööd. Mehaanilist tööd tehakse siis, kui keha liigub mingi jõu mõjul. Lükates kappi ühest kohast teise, kulutame energiat ja teeme mehaanilist tööd. Üritades lükata seina või näiteks veoautot, me küll väsime, kuid mehaanilist tööd samal ajal ei tee, kuna sein või veoauto ei liigu.
Mehaaniline töö võrdub kehale rakendatud jõu ning selle jõu mõjul läbitud teepikkuse korrutisega.
Kapi nihutamisel kolme meetri võrra teeme kolm korda rohkem tööd kui kapi nihutamisel ühe meetri võrra. Kelgu vedamiseks jäisel lumel kulutame palju vähem energiat (teeme vähem tööd) kui kelgu vedamiseks liivatatud lumel, kuna hõõrdejõud jääl on palju väiksem ja seega peame rakendama palju väiksemat jõudu. Füüsikas tähistatakse tehtud tööd tavaliselt tähega A, jõudu tähega F ning teepikkust tähega s. Vastavalt saame töö definitsiooni kirja panna valemiga:
Töö ühikuks on džaul (lühend J). Tehtud töö suuruseks on 1 džaul siis, kui kehale rakendatakse jõudu 1 njuuton ning keha liigub selle mõjul 1 meetri: 1 J = 1N · m.
Näidisülesanne
Kui palju tööd peab tegema koer, et vedada kelku 100 meetri kaugusele? Kelk koos koormaga kaalub 150kg ning hõõrdejõud kelgu ja lume vahel moodustab 3% kelgule mõjuvast raskusjõust.
Lahendus
Kelgu ühtlase vedamise korral on koera veojõud võrdne kelgule mõjuva hõõrdejõuga.
Andmed
mkelk=150kg
s=100m
p=3%––––––––
A−?
Arvutused
Vastus. Koer peab tegema tööd 4,4kJ.
Aga kuidas jääb energiaga? Mis see on, kust seda saab ja kui palju seda kulub?
Füüsikas nimetatakse energiaks keha (või kehade süsteemi) võimet teha tööd. Näiteks omab Maa gravitatsiooniväljas üles tõstetud pall energiat – lastes palli lahti, hakkab see raskusjõu mõjul allapoole liikuma ja sealjuures tehakse mehaanilist tööd. Kuna tööd tehakse energia arvelt, siis on ka energia ühikuks džaul.
Alljärgnevast kahest pildist vasakpoolsel toodetakse inimestele füüsika poolt käsitletavat energiat. Ka laulukaare alt saavad inimesed energiat, aga see on üks hoopis teistmoodi energia, mida füüsika seni veel ei käsitle.
Kui palju energiat kulub ühe või teise töö tegemiseks? Mehaanilise tööga on lihtne – kui me teeme kapi nihutamiseks mehaanilist tööd 10 džauli, siis me kulutame selleks ka energiat 10 džauli.
Aga kui palju vajab rakett või lennuk energiat, et sihtkohta jõuda? Kui kaugele saab elektriautoga ühe laadimisega sõita? Kui palju peaks sööma pärast väsitavat füüsilist trenni? Aga pärast malemängu? Reaalse elu probleemid on reeglina palju keerulisemad kui need, millega me siin õpikus tegeleme. Aga selles osas ei erine teadus palju viiulimängust – võib ju üritada kohe Paganini esimest viiulikontserti mängima hakata, aga pigem tasuks alustada poogna õigest hoidmisest ja mõnest lihtsamast muusikapalast.
Mehaaniline töö
Mehaanilist tööd tehakse siis, kui keha liigub mingi jõu mõjul. Mehaaniline töö võrdub kehale rakendatud jõu ning selle jõu mõjul läbitud teepikkuse korrutisega:
Töö ühikuks on džaul (lühend ). Tehtud töö suuruseks on 1 džaul siis, kui kehale rakendatakse jõudu njuuton ning keha liigub selle mõjul meetri: .
Energiaks me nimetasime keha võimet teha tööd. Aga kumb õun on võimeline rohkem tööd tegema, kas see, mille endale pealaele asetame, või see, mis meile puu otsast pähe kukub? Kas liikumisel on ka energia? Aga puu otsas rippumisel?
Puu otsas rippuvale õunale mõjub raskusjõud. Kui õun tuleb oksa küljest lahti, kukub see maha. Me oskame arvutada ka kukkudes tehtava töö – kui õun massiga m kukub kõrguselt h alla, siis saame kirjutada:
kus F = mg on õunale mõjuv raskusjõud. Kuna läbitud teeks on kõrguste vahe, siis oleme selle tähistanud tähega h. Kus on selles pildis energia?
Me teame, et puu otsas rippuva õuna ja Maa vahel toimib gravitatsiooniline vastastikmõju ja õuna alla kukkumisel teeb tööd gravitatsioonijõud. Järelikult on otsitav energia „salvestunud“ gravitatsioonilises vastastikmõjus. See energia on õunal puu otsas rippudes kogu aeg olemas, aga see vabaneb, st hakkab tööd tegema alles hetkel, kui õuna vars puu küljest lahti tuleb ja õunal tekib võimalus alla kukkuda.
Energiat, mida kehad omavad vastastikmõju tõttu, nimetatakse potentsiaalseks energiaks.
Maapinnast kõrgusel h olev õun omab niisiis potentsiaalset energiat:
Kui õun hakkab puu otsast kukkuma, siis õuna potentsiaalne energia väheneb, sest õun läheneb maapinnale. Aga energia ei saa lihtsalt ära kaduda. Kukkuva õuna kiirus kasvab ning selle potentsiaalne energia muutub liikumise energiaks ehk kineetiliseks energiaks.
Kineetiliseks energiaks nimetatakse energiat, mida keha omab liikumise tõttu.
Kehade kineetilise ja potentsiaalse energia summat me nimetame keha mehaaniliseks koguenergiaks. Oletame hetkeks, et keha liikumist ei takista kõrvalised jõud – näiteks kukkuva õuna korral puudub õhutakistus, veereva palli korral puudub hõõrdumine. Sel korral kehtib mehaanilise energia jäävuse seadus, mis ütleb, et keha või kehade süsteemi mehaaniline koguenergia ei muutu, see on jääv suurus:
Selgub, et keha kineetiline energia sõltub keha massist ja keha kiirusest kujul
Pange tähele – valemis on kiiruse ruut. See tähendab muuhulgas seda, et sõites autoga kaks korda kiiremini, on auto kineetiline energia neli (22 = 4) korda suurem. Järelikult on ka auto pidurdusteekond kaks korda suurema kiiruse korral umbes neli korda suurem.
Näidisülesanne
Millise kiirusega põrkab 100grammine pall vastu maad, kui ta lasta nelja meetri kõrguselt alla kukkuda?
Lahendus
Algselt on pallil ainult potentsiaalne energia. Kineetiline energia on null, kuna pall ei liigu. Maapinnale jõudes muutub palli kogu potentsiaalne energia kineetiliseks energiaks.
Andmed
h=4m
m=100g=0,1kg–––––––––––––––––––––
v−?
Arvutused
Vastus. Nelja meetri kõrguselt lahti lastud pall põrkab vastu maad kiirusega .
Ühe ja sama massiga õpilased teevad 400 meetri läbimisel sama palju mehaanilist tööd, kuid ometi kulub ühel õpilasel selle distantsi läbimiseks 60, teisel 70 sekundit. Töö tegemise kiirust iseloomustab võimsus. See õpilane, kes jooksis kiiremini, tegi ühes sekundis rohkem tööd, tema võimsus oli suurem.
Võimsus on füüsikaline suurus, mis väljendab ühe ajaühiku jooksul tehtud töö hulka (ehk kulutatud energiat). Võimsust tähistatakse tähega N ning seda saab arvutada valemiga:
Võimsuse ühikuks on vatt (lühend W): 1 W = 1 J / 1 s. Võimsus 1 vatt on väga väike võimsus. Rahulikult kõndides on inimese võimsus umbes 50 W. Paljude sõiduautode võimsus jääb vahemikku 70–120 kW, mis tähendab, et ühes sekundis teevad need autod tööd 70–120 kJ.
| Hubble'i kosmoseteleskoobi orbiidile saatmine (STS-31). 30 000 kN jõud tõstab 2000 tonni kaaluva kosmosesüstiku Discovery. Süstiku kaubaruumis on Hubble'i kosmoseteleskoop. | Võimsuse mõõtmiseks kasutatakse tihti ka mõõtühikut hobujõud (tähis hj). Selle mõõtühiku võttis kasutusele Šoti insener James Watt 18. sajandil, et võrrelda veohobuste ja aurumootorite võimsusi. Hobujõu suurus on 735,499 vatti. Inglismaal ja USAs on hobujõu suurus 745,7 vatti. |
Näidisülesanne
Kui suurt keskmist võimsust arendab inimene, kes tõstab 2 sekundiga 0,4m kõrgusele 50kg kaaluva kivi?
Lahendus
Võimsuse arvutamiseks on meil vaja teada seda, kui palju tehakse tööd. Kivi tõstmiseks peame ületama raskusjõu, seega on kivi tõstmiseks kõrgusele tehtav töö kivile mõjuva raskusjõu ja läbitud teepikkuse () korrutis.
Andmed
t=2s
h=0,4m
m=50kg–––––––––––
N−?
Arvutused:
Vastus. Kivi tõstmisel arendab inimene keskmiselt võimsust 100W.
| See on RT-flex96C, väidetavalt maailma kõige võimsam diiselmootor, mille on loonud ja mida toodab Soome firma Wärtsilä. Mootor on 13,5 m kõrge ja 26,59 m pikk ning kaalub 2300 tonni. Võimsust suudab see arendada kuni 80 000 kW. | Gordoni jõe tamm Tasmaanias on 140 m kõrge ning selle kaar on 190 m pikk. Kaare paksus on kõige jämedamas kohas (all) 17,7 m ning kõige õhemas kohas (üleval) 2,75 m. Kolmele 450 MW koguvõimsusega generaatorile annab hoogu 11,3 km3 vett mahutav Gordoni veehoidla. Võrdluseks: näiteks Peipsi järve maht on 25 km3. |
Võimsus
Võimsus on füüsikaline suurus, mis väljendab ühe ajaühiku jooksul tehtud töö hulka (ehk kulutatud energiat). Võimsust tähistatakse tähega ning seda saab arvutada valemiga:
Võimsuse ühikuks on vatt (lühend ): 1W=1J/1s.
Jalgrattaga sõites väntame pedaale, kuid ratast ajab ringi kettülekanne. Kivi saame kergemini august kätte kangi abil. Auto ratta vahetamiseks tõstetakse auto üles tungrauaga. Koormiste tõstmiseks kasutatakse plokke ja talisid. Salvkaevust saame vee kätte pööra käepidet keerates. Miks nii?
Kõik mainitud abivahendid koosnevad ühest või mitmest lihtmehhanismist.
Lihtmehhanismid on lihtsa ehitusega (ilma mootorita) seadmed, millega muudetakse ülekantava jõu suurust või suunda.
Kui asetame toetuspunktile pika jäiga ridva, siis oleme saanud lihtmehhanismi, mida nimetatakse kangiks. Uurime, kui palju tööd me peame tegema, et tõsta kivi kangiga august välja.
Kivi tõstmiseks 20 cm kõrgusele peame tõstma kivi jõuga
Seega töö, mida peame tegema, on
Me kasutame kahemeetrist kangi. Kivi on kangi toetuspunktist 40 cm kaugusel ning meie käsi on toetuspunktist 160 cm kaugusel. Et kangi kiviga ots tõuseks 20 cm võrra, peab kangi teist otsa alla vajutama 80 cm võrra – meie käsi on kangi toetuspunktist neli korda kaugemal, seega peab meie käsi läbima ka neli korda pikema tee. Töö, mida peame kivi tõstmiseks tegema, on 196 J. Seega teades, kui pika tee meie käsi läbib, saame leida jõu, millega peame kangi vajutama.
Ilma kangita oli vaja kivile rakendada jõudu 980 N, mis on neli korda rohkem kui kangi kasutades.
Kõikide lihtmehhanismide kohta saame kirja panna seaduspärasuse.
Lihtmehhanismid ei muuda töö hulka, mida tuleb teha. Lihtmehhanism muudab vajaminevat jõudu ja läbitud teepikkust. Nii mitu korda, kui lihtmehhanismi kasutamisel võidetakse jõus, kaotatakse läbitud tee pikkuses, ja vastupidi.
Seda seaduspärasust tuntakse kui mehaanika kuldreeglit.
Mehaanika kuldreegel väidab, et töö, mida peame tegema, on alati sama suur ega sõltu sellest, kas me kasutame lihtmehhanisme või mitte. Tegelikult peame lihtmehhanisme kasutades tegema alati rohkem tööd kui ilma nendeta, sest osa energiat kulub hõõrdejõudude ületamiseks lihtmehhanismide sees. Näiteks veeretades keha mööda kaldpinda üles, peame rakendama jõudu nii keha ülespoole liigutamiseks kui ka hõõrdejõu ületamiseks. Ilma kaldpinnata on meil vaja ainult rakendada jõudu keha tõstmiseks.
Seda, kui suure osa tehtud tööst moodustab kasulik töö, näitab kasutegur. Raskuse tõstmisel on kasulik töö see, mis kulub gravitatsioonijõu ületamiseks. Kogutöö, mis tehakse, on alati kasulikust tööst suurem, kuna lisaks töö tegemisele peame kulutama energiat hõõrdejõu (või mõne teise takistusjõu) ületamiseks. Kasuteguriks nimetatakse kasuliku töö suhet kogutööga:
Enamasti antakse kasutegur protsentides:
Lihtmehhanismid, kang
Lihtmehhanismid on lihtsa ehitusega (ilma mootorita) seadmed, millega muudetakse ülekantava jõu suurust või suunda. Kui asetame toetuspunktile pika jäiga ridva, siis oleme saanud lihtmehhanismi, mida nimetatakse kangiks.
Mehaanika kuldreegel
Lihtmehhanismid ei muuda töö hulka, mida tuleb teha. Lihtmehhanism muudab vajaminevat jõudu ja läbitud teepikkust. Nii mitu korda, kui lihtmehhanismi kasutamisel võidetakse jõus, kaotatakse läbitud tee pikkuses, ja vastupidi.
Asetades joonlaua pliiatsi peale, saame kõige lihtsama kangi. Joonlaud on tasakaalus, kui pliiats on täpselt joonlaua keskel. Asetades joonlaua otstele erineva massiga koormised, tuleb pliiatsi asukohta (joonlaua toetuspunkti) muuta, et ta oleks jätkuvalt tasakaalus. Mida kaugemal on koormis toetuspunktist, seda suurem on selle pöörav toime, nii et samasuguse toime saavutamiseks tuleb kergem koormis kangi toetuspunktist kaugemale asetada.
Jõu pöörava toime iseloomustamiseks on vaja kasutusele võtta jõu õla mõiste. Jõu õlg on kaugus kangi keskpunktist jõu rakenduspunktini. Jõu õlga tähistatakse tavaliselt tähega l. Kasutades jõu õlga, saame kirja panna kangi reegli ehk kangi tasakaalu tingimuse:
Kui kangi üks jõu õlg on teisest mingi arv kordi pikem, siis võib sinna rakendada sama arv kordi väiksemat jõudu, et kang püsiks tasakaalus.
Näidisülesanne 1
Ühe meetri pikkuse puitvarda ühe otsa külge on riputatud 100grammine raskus ning teise otsa külge 300grammine raskus. Kui kaugel peab olema toetuspunkt varda otsast, kui tahame, et varras oleks tasakaalus? Puitvarda massiga ei ole vaja arvestada.
Lahendus
Kang on tasakaalus, kui mõlemal pool olevate raskuste raskusjõudude ja jõu õlgade korrutised on võrdsed. Tähistame vasakul pool oleva jõu õla -ga ning paremal pool -ga. Kuna kogu kangi pikkus on meeter, siis l2=1m−l1.
Andmed
m1=100g
m2=300g
l=1m––––––––
l1−?
l2−?
Arvutused
Kuna
siis saame
Vastus. Toetuspunkt peab olema raskusest 25cm kaugusel.
Näidisülesanne 2
Milline peab olema tundmatu massiga keha mass, et kang oleks tasakaalus?
Lahendus
Paremal pool mõjutab kangi ainult üks koormis. Vasakul pool mõjutab kangi kaks koormist. Kang on tasakaalus, kui vasakul pool olevate koormiste raskusjõudude ja jõu õlgade korrutiste summa on võrdne paremal pool oleva koormise raskusjõu ja jõu õla korrutisega.
Andmed
m1=200g
m2=50g
l1=10cm
l2=20cm
l3=10cm–––––––––––
m3−?
Arvutused
Avaldades viimasest võrrandist , saame
m3=200g⋅10cm−50g⋅10cm10cm=100g––––––––––––
Vastus. Tundmatu massiga keha peab kaaluma 100g, et kang oleks tasakaalus.
Jõu õlg. Kangi tasakaalu tingimus
Jõu õlg on kaugus kangi keskpunktist jõu rakenduspunktini. Kangi reegli ehk kangi tasakaalu tingimuse saab kirja panna valemiga
Kangi tasakaalu tingimus ütleb, et kui kangi üks jõu õlg on teisest mingi arv kordi pikem, siis võib sinna rakendada sama arv kordi väiksemat jõudu, et kang püsiks tasakaalus.
Looduses on võnkumine loomulik nähtus. Puuoksad kõiguvad tuules, puulehed värisevad oksa küljes, lind liigutab oma tiibu lendamise ajal üles-alla. Võnkliikumiseks ehk võnkumiseks nimetatakse liikumist, mis kordub kindla ajavahemiku järel.
Uurime niidi abil toe külge kinnitatud kuuli liikumist. Füüsikas nimetatakse sellist võnkuvat keha pendliks.
Kui pendlit lükata, siis hakkab see edasi-tagasi liikuma. Asendit, kus kuul algul paigal püsis, nimetatakse tasakaaluasendiks. Kõige kaugemat punkti tasakaaluasendist, kuhu pendel liigub, nimetatakse amplituudasendiks. Selles asendis jääb pendel hetkeks seisma ning hakkab tagasi liikuma. Kaugust tasakaaluasendist amplituudasendini nimetatakse amplituudiks. Täisvõnkeks nimetatakse pendli liikumist ühest amplituudasendist teise ning tagasi esimesse.
Korraldasime katse, kus mõõtsime, kui palju aega kulub pendlil 5, 10, 15 ja 20 täisvõnke tegemiseks. Katse tulemused kandsime tabelisse.
Andmetest saame teada, et 10 täisvõnke tegemiseks kulus pendlil 20 sekundit. Sellest saame järeldada, et ühe täisvõnke tegemiseks kulub pendlil 2 sekundit. Sama tulemuseni jõuame kõikide katsete korral.
Ajavahemikku, mis kulub võnkuval kehal ühe täisvõnke tegemiseks, nimetatakse selle keha võnkeperioodiks. Lisaks võnkeperioodile saab pendlit iseloomustada võnkesagedusega. Võnkesagedus näitab, mitu täisvõnget teeb võnkuv keha ühes ajaühikus.
On lihtne näha, et võnkesagedus ja võnkeperiood on omavahel seotud. Kui pendli võnkeperiood on kaks sekundit, siis kahe sekundi jooksul teeb selline pendel ühe täisvõnke. Seega ühe sekundi jooksul teeb pendel pool täisvõnget ja pendli võnkesagedus on pool võnget sekundis.
Matemaatiliselt saame võnkesageduse ja võnkeperioodi omavahelise seose kirja panna valemiga
See valem saab füüsikas tavapäraste tähistustega kirja pannes kuju
Sageduse ühik on herts (lühend Hz). 1 Hz on selline sagedus, mille korral võnkuv keha teeb ühe täisvõnke sekundis, st
Pendli liikumine on hea näide sellest, kuidas mehaanilisel liikumisel kineetiline ja potentsiaalne energia teineteiseks muunduvad. Seda protsessi kirjeldab alljärgnev joonis.
Miks jääb võnkuma pandud pendel mõne aja pärast siiski seisma? Pendli liikumist takistab õhk, nii et osa selle kineetilisest energiast kulub õhutakistuse ületamisele. Mehaanilise energia jäävuse seaduses tähendab see mehaanilise koguenergia vähenemist, väheneb ka pendli maksimaalne potentsiaalne energia. Järelikult väheneb ka võnkumise amplituud ja mõne aja pärast jääb pendel seisma.
| Veel üsna hiljuti olid pendelkellad hinnatud ajamõõtjad. Uuri seda joonist. Kas saad aru, miks pendel seisma ei jää, ehkki selle liikumist takistab nii hõõrdumine kui ka õhk? | F. L. Löbneri Saksamaal valmistatud pendelkell. Eesti õige aja teenistuse peakell 1920-1940, mida kontrolliti Naueni või Eiffeli torni raadiojaama ajasignaalide järgi. Üle Eesti saadeti tähetornist signaal |
Näidisülesanne
Vaatleme pendlit, mis võngub sagedusega 2Hz. Milline on pendli võnkeperiood?
Lahendus
Andmed
Arvutused
Võnkeperiood ja sagedus on omavahel seotud valemiga . Teades sagedust, saame arvutada pendli võnkeperioodi:
Helid ümbritsevad meid kõikjal. Looduses kuuleme puude sahinat, linnulaulu, kaugel maanteel sõitva auto mürinat jne. Helide kaudu saame ka märkimisväärse osa infost meid ümbritseva maailma kohta – me teame, et puud sahisevad, lind laulab ja autod sõidavad ka ilma, et me kõike seda näeksime.
Teame oma kogemuse põhjal, et heli tekitamiseks on tarvis midagi kiiresti võnkuma panna. Parim viis selleks on elastne ese tasakaaluasendist välja viia ning siis lahti lasta. Võime näiteks üle laua serva ulatuva joonlaua põrisema panna. Kitarri keeled hakkavad helisema, kui neid tasakaaluasendist eemale tõmmata ja siis lahti lasta. Trumm teeb häält siis, kui seda lüüa. Kõik need kehad võnguvad kiiresti. Võnkuvat keha nimetatakse heliallikaks.
Miks me kuuleme heli? Heli levimist ruumis võib võrrelda laine liikumisega veekogus, millesse on visatud kivi. Kivi vette kukkumise kohta tekib laine, see kandub üle veekogu edasi ja paneb võnkuma ka seal hulpivad puupilpad.
Võnkuv joonlaud paneb koos endaga võnkuma joonlauda ümbritseva õhu osakesed. Need osakesed mõjutavad sellest kaugemal olevaid õhu osakesi, need omakorda järgmisi jne. Lõpuks jõuab võnkumine kõrvas oleva trummikileni ning seda me tajume helina.
Laineks nimetatakse võnkumise levimist keskkonnas.
Kuna heli levimisel puudub otsene vastasmõju heli allika ja vastuvõtja vahel, võnkumised levivad osakeselt osakesele, siis võtab heli levimine paratamatult aega. Katseliselt on kindlaks tehtud, et õhus on heli levimise kiirus umbes 340 m/s.
Teades heli levimise kiirust, võime hinnata, kui kaugel välku lööb. Selleks tuleb lugeda sekundeid välgulöögist kuni müristamiseni. Tõepoolest, kuna valgus levib võrreldes heliga väga kiiresti, u 300 000 km/s, ja jõuab vaatlejani peaaegu hetkeliselt, siis saame niimoodi teada aja, mis kulus helilainel meieni jõudmiseks. Sellest omakorda saab heli kiirust teades arvutada teepikkuse. Kuuldes müristamist kolm sekundit pärast välgulööki, tead, et välgu sähvatus toimus sinust umbes ühe kilomeetri kaugusel.
Heli saab levida ka tahkistes ja vedelikes. Kuna sellistes keskkondades on aineosakesed üksteisele palju lähemal, kandub võnkumine edasi palju kiiremini. Heli levimise kiirus erinevates keskkondades on toodud kõrvalolevas tabelis.
Kindlasti oled kuulnud suures ruumis rääkides oma hääle kaja. Kaja tekib sellepärast, et hääl, mida sina tekitad, levib ruumi seinteni, peegeldub nendelt ning jõuab sinuni tagasi. Kaja tekib alati, kui heli teel on takistus, aga vaid suures ruumis (piisavalt kaugete takistuste korral) võtab seinani ja tagasi levimine nii palju aega, et kaja oleks võimalik otse allikast tulevast helist eristada. Eriti kaua tuleb kaja oodata, kui hüüda kauge metsa või mäe poole. Tasub proovida, sest niimoodi saab ka ligikaudu teada metsa või mäe kauguse. Mõnikord võib kuulda ka kahte kaja, kui heli peegeldub kahelt eri kaugusel olevalt takistuselt.
Heli peegeldumist (kaja) kasutatakse näiteks kajaloodi töös, kui on vaja merepõhja sügavust määrata või vee alt kalaparvi otsida. Kajalood saadab merepõhja ultrahelisignaali ning registreerib aja, millal signaal tagasi laeva peegeldub. Teades heli levimise kiirust vees, saame arvutada merepõhja sügavuse.
Sama põhimõtet kasutades on võimalik ultraheliga naise kõhus olevat loodet vaadata. Ultrahelilained suunatakse lootele ning registreeritakse aeg, millal peegeldunud heli tagasi jõuab. Kuna erinevatelt loote osadelt võtab peegeldumine erineva aja, on võimalik erinevatest suundadest ultraheli peegeldumise registreerimisega saada lootest pilt.
Looduses kasutavad kajalokatsiooni näiteks nahkhiired ja delfiinid.
Heli tekkimine ja levimine
Heli tekitamiseks on tarvis midagi kiiresti võnkuma panna. Võnkuv keha paneb koos endaga võnkuma joonlauda ümbritseva õhu osakesed. Need osakesed mõjutavad sellest kaugemal olevaid õhu osakesi, need omakorda järgmisi jne. Seda nähtust me nimetamegi heliks ja selle levimiseks. Võnkuvat keha nimetatakse heliallikaks. Heli levimise kiirus õhus on ca 340m/s.
Me räägime kõrgest ja madalast helist. Näiteks lauljatest sopranid suudavad tekitada kõrgeid helisid ning bassid madalaid helisid. Aga miks on helid erineva kõrgusega?
Kordame joonlaua katset, muutes üle laua serva ulatuva joonlaua osa pikkust. Kindlasti märkate, et kui joonlaud on vaid veidi üle laua serva, kuuleme joonlaua võnkudes kõrget heli. Mida rohkem aga nihutame joonlauda üle laua serva, seda madalamat heli selle võnkudes kuuleme. Ühtlasi näeme, et mida lühem osa on laua servast üle, seda „kiiremini“ joonlaud võngub. Sellest joonlaua võnkumise „kiirusest“ heli kõrgus sõltubki. Kui joonlaud võngub kiiremini, on selle võnkesagedus suurem ning heli, mida kuuleme, kõrgem. Mida suurem on heliallika võnkesagedus, seda kõrgemat heli see tekitab.
Kõik võnkuvad kehad tekitavad heli, kuid inimene ei ole võimeline kõiki neid helisid kuulma. Madalaimaks helisageduseks, mida inimene kuuleb, loetakse 16 Hz ning kõrgeimaks sageduseks 20 000 Hz. Heli sagedusega alla 16 Hz nimetatakse infraheliks. Suurema kui 20 000 Hz sagedusega heli nimetatakse ultraheliks. Ultraheli täiskasvanud inimesed ei kuule, kuid on tõestatud, et imikud kuulevad ka ultraheli.
| Koeravile – inimesed seda ei kuule, kuna see tekitab ultraheli. | Saksofonide ja viiulite pered. Pildil on näidatud muusikariista pikkuse seos temast tuleva heliga. Iga muusikariista sagedusvahemik on tähistatud horisontaalse ribaga sageduste skaalal, milleks on kõige all asuv klaviatuur. Sagedus suureneb paremale poole. |
Lüües käega rahulikult trummi, tekib vaikne heli, kuid lüües trummi pihta kõvasti, tekib vali heli. Sagedus, millega trumm võnkuma hakkab, on mõlemal juhul sama, kuid see, millise amplituudiga trumm võnkuma hakkab, on erinev. Heli valjus ehk heliintensiivsus sõltub sellest, millise amplituudiga heliallikas võngub.
| Suurema amplituudiga võnkumine tekitab valjema heli. | Heli valjuse mõõtmiseks on igaühel võimalik oma nutitelefoni leida soblik rakendus (nt otsisõnaga soundmeter). Tuleb siiski tähele panna, et tihti ei näita need rakendused päris õiget väärtust ja usaldusväärsete tulemuste saamiseks tuleks rakendus kalibreerida. |
Heliintensiivsuse ühikuna kasutatakse kõige sagedamini detsibelli (dB). Keskmiselt hakkab inimene kuulma heli, mille valjus on 0 dB (see vastab rõhule 2 · 10-5 Pa). Vaikse häälega rääkides on heliintensiivsus umbes 20–30 dB. Kui heliintensiivus on suurem kui 130 dB, siis tekitab see inimese kõrvas valuaistingu – kõrvas asuv trummikile hakkab liiga suure amplituudiga võnkuma. Heli, mille valjus on 180 dB, loetakse inimese jaoks surmavaks.
Inimese kõrv on kaugelt tundlikum ja täiuslikum, samas ka keerukam seade kui mistahes mikrofon. Selles veendumiseks piisab, kui uurida alljärgnevat joonist. Siinkohal saame anda vaid väga ligikaudse kirjelduse sellest, mismoodi me helisid kuuleme. Hoidke ja säästke oma kuulmist – liiga vali heli, üldse igasugused kiired rõhu muutused võivad seda kahjustada. Ja kord juba tekkinud kahju on väga keeruline parandada.
Heli kõrgus
Mida suurem on heliallika võnkesagedus, seda kõrgemat heli see tekitab. Madalaimaks helisageduseks, mida inimene kuuleb, loetakse 16 Hz ning kõrgeimaks sageduseks 20 000 Hz. Heli sagedusega alla 16 Hz nimetatakse infraheliks. Suurema kui 20 000 Hz sagedusega heli nimetatakse ultraheliks.
Heli tekitamiseks on vaja võnkuvat keha, olgu selleks siis helihark või viiuli kõlakoja seinad. Aga mitte kõik helid ei ole meile ühtviisi meeldivad.
Kui viiul juhtub häälest ära olema või ei ole mängijal piisavalt oskusi, kostub sealt kägin, mida vaid mööndustega saab heliks nimetada. Haamriga plekitükki kolkides me tekitame müra. Müra kuuleme ka siis, kui paljude heliallikate tekitatud helid liituvad korrapäratult.
Kodus tekitavad müra näiteks kodumasinad – külmkapp, pesumasin, arvuti, tolmuimeja jne. Koolis tekitavad müra peamiselt lapsed. Müra tekitamiseks ei pea lapsed kõvasti rääkima ega jooksma, piisab sellest, et nad räägivad korraga. Sellisel juhul helilained liituvad ning tulemuseks on korrapäratu õhuosakeste võnkumine – see ongi müra.
Müra on inimese tervisele kahjulik. Pidev müras viibimine väsitab ning tekitab peavalu. Inimene võib küll müraga harjuda ega pane seda enam tähelegi, kuid sellele vaatamata kahjustab müra tervist.
Samas ei pruugi igasugune müra olla alati kahjulik. Looduses tekkiv müra, nagu puude kahin või mere kohin, mõjub enamasti pigem rahustavalt.
Kahjuliku müra eest on vaja ennast kaitsta. Töötades müra tekitavate masinatega, tuleb kanda müra summutavaid kõrvaklappe.
Lisaks kuuldavale helile levib meie ümber ka madalasageduslik infraheli. Infraheli me ei kuule ja me ei tea, kas asume selle mõjualas või mitte. Infraheli tekib looduses tugeva tuulega, maavärinates ja laviinides. Mitmed loomad, nagu näiteks elevandid ja vaalad, kasutavad infraheli suhtlemiseks. Tehislikku infraheli tekitavad ka näiteks tuulikud.
31. mail 2003. aastal viis rühm Ühendkuningriikide uurijaid läbi eksperimendi, kus nad lasid umbes 700 inimesel kuulata muusikat, millele oli lisatud vaevu kuuldav 17 Hz infraheli toon. Infraheli tekitamiseks kasutasid nad spetsiaalset, eriti suure võnkeamplituudiga kõlarit, mis oli kinnitatud seitsme meetri pikkuse plastiktoru külge. Peaaegu veerand eksperimendis osalenutest kaebas rahutust, ebamugavustunnet, äärmist kurbust, närvilisust, hirmupuhanguid, külmavärinaid või surutusetunnet rinnus. Oma kõnes ütles professor Richard Wiseman: „Need tulemused viitavad, et madalsageduslik heli võib inimestes esile kutsuda ebaharilikke kogemusi, isegi kui nad ei suuda infraheli kuulda. Teadlased on oletanud, et selliseid helisid võidakse kasutada mõnes väidetavalt nõiutud kohas veidrate aistingute esile kutsumiseks, mida inimesed vaimudega seostavad. Meie tulemused igatahes kinnitavad seda oletust.“
Millised on maailma kõige vaiksemad kohad? Täieliku vaikuse saavutamiseks ehitatakse spetsiaalseid ruume, kus on hoolitsetud nii selle eest, et väljastpoolt ükski heli sisse ei pääseks, kui ka selle eest, et ruumis sees tekitatud helid ruumi seintelt tagasi ei peegelduks.
| Väga vaikne ruum Fraunhofferi instituudis Saksamaal. Siin on hoolitsetud ka selle eest, et puuduks igasugune kaja. Ruumi kasutatakse akustilisteks täppismõõtmisteks. | Spetsiaalsed kõrvatropid muusikutele. Sellised kõrvatropid vähendavad kõrva jõudva heli valjust ilma seda moonutamata. Paljudel teenekatel muusikutel esineb akuutne kuulmisvaegus, kuna nad on pikka aega viibinud väga valju heliga keskkonnas. Sellised kõrvatropid aitavad kuulmisvaeguseid ära hoida. |
Muidugi, võib minna ka kosmosesse – kui ei ole õhku, siis ei ole ka heli, on täielik rahu ja vaikus.