Ühtlaselt muutuva liikumise liikumisvõrrand ja liikumisgraafik

Speed graph

Ühtlase liikumise kiiruse graafik on horisontaalne sirgjoon

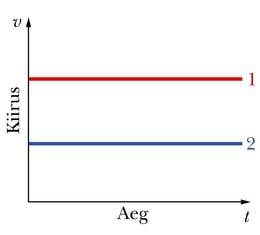
Kui liikumisgraafik näitab keha koordinaadi sõltuvust ajast, siis kiiruse graafik kiiruse sõltuvust ajast. Kiiruse graafiku püstteljele kantakse kiiruse väärtused ja horisontaalteljele sarnaselt liikumisgraafikuga aeg. Kõige lihtsam kiiruse graafik on ühtlasel liikumisel. Kuna ühtlasel liikumisel kiirus ei muutu, on selle väärtus igal ajahetkel sama ja graafikuks on horisontaalne sirgjoon (vt joonist). Kiirema liikumise korral asub graafik teljestikus kõrgemal ja aeglasema korral madalamal positsioonil.

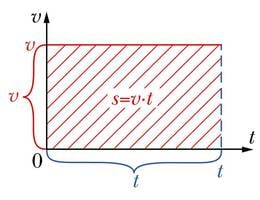
Nihke pikkus on võrdne kiiruse graafiku alla jääva pindalaga

Kuigi kiiruse graafikul on näidatud vaid kiiruse sõltuvus ajast, saab selle abil ka sooritatud nihke pikkuse leida. Vaatame ühtlase liikumise graafikut. Kui märgime sellel ära ajavahemiku 0 kuni t, saame ristküliku, mille külgede pikkusteks püstsihis on kiirus v ja horisontaalsihis aeg t. Selle ristküliku pindala on võrdne külgede pikkuste korrutisega ehk v•t. Kiiruse ja liikumiskorrutise korrutis on aga võrdne sooritatud nihke pikkusega: s = vt. Jõudsime olulise tulemuseni: kiiruse graafiku alla jääv pindala on võrdne keha poolt sooritatud nihke pikkusega. See kehtib mitte ainult ühtlase, vaid ka muutuva liikumise korral.

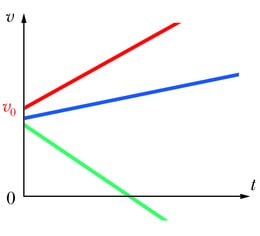
Ühtlaselt muutuva liikumise kiiruse graafikuks on tõusev või langev sirge

Ühtlaselt muutuva liikumise korral muutub kiirus võrdsetes ajavahemikes sama palju ja kiiruse graafikuks on tõusev või langev sirge. Graafiku tõus või langus on seda suurem, mida kiiremini kiirus muutub ehk mida suurem on kiirendus. Tõusva graafiku korral liikumine kiireneb, langeva korral aeglustub. Kui graafik on ajateljest allpool, on kiirus negatiivne, liikumine toimub koordinaattelje negatiivses suunas ning langev graafik tähistab sel juhul kiiruse kasvamist. Graafiku lõikepunkt püstise kiiruse teljega annab kiiruse hetkel t = 0 ehk algkiiruse v₀. Kui graafik pole sirge, on tegemist mitteühtlaselt muutuva liikumisega.

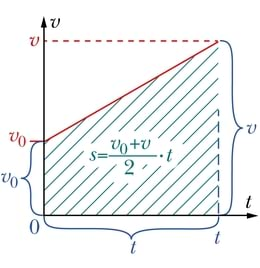
Ühtlaselt muutuva liikumise nihe ja liikumisvõrrand

Selleks, et tuletada valem, mis näitaks ühtlaselt muutuva liikumise korral nihke sõltuvust ajast, saame kasutada teadmist, et nihke pikkus on võrdne kiiruse graafiku alla jääva pindalaga. Olgu keha kiirus alghetkel v₀ ja saavutagu aja t möödumisel väärtuse v. Kiiruse graafikuks on tõusev sirge, mille alla jääv kujund on trapets, mille alusteks on kiirused v₀ ja v ning kõrguseks aeg t.

Aja t jooksul keha poolt sooritatava nihke pikkus on võrdne selle trapetsi pindalaga, mille leidmiseks tuleb aluste poolsumma korrutada kõrgusega:

(1.13)

s = \frac{v_{0} + v}{2} t = \frac{v_{0} t}{2} + \frac{v t}{2}

Teades seosest (1.12 ), et kiirus avaldub kiirenduse kaudu kujul v = v₀ + at, saame pärast asendamist

(1.14)

s = \frac{v_{0} t}{2} + \frac{(v_{0} + a t) t}{2}

mille lihtsustamisel jõuamegi avaldiseni, mis näitab nihke sõltuvust ajast ühtlaselt muutuval liikumisel:

(1.15)

s = v_{0} t + \frac{a t^{2}}{2}

Näeme, et nihe sõltub ajast ruutfunktsiooni järgi. Mõne probleemi lahendamisel pole liikumise aeg teada, küll aga on teada lõppkiirus. Sel juhul leitakse aeg kiiruse valemist (1.12’ )

(1.16)

t = \frac{v - v_{0}}{a}

Selle ajaga asendamisel omandab seos (1.13 ) kuju

(1.17)

s = \frac{(v_{0} + v)}{2} \cdot \frac{(v - v_{0})}{a}

ehk

(1.17)

s = \frac{(v + v_{0})}{2} \cdot \frac{(v - v_{0})}{a}

Pärast lihtsustamist ruutude vahe valemi abil saame nihke arvutamiseks valemi:

(1.18)

s = \frac{v^{2} - v_{0}^{2}}{2 a}

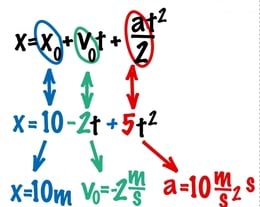
Teades nihke sõltuvust ajast, on liikumisvõrrandit lihtne koostada. Näitab ju see võrrand keha koordinaadi sõltuvust ajast ja nagu ütleb seos (1.6 ), saame keha koordinaadi arvutada mis tahes ajahetke jaoks, liites algkoordinaadile selleks hetkeks sooritatud nihke pikkuse: x = x₀ + s. Lähtudes nihke avaldisest (1.15 ), näeme, et ühtlaselt muutuva liikumise liikumisvõrrandiks on

(1.19)

x = x_{0} + v_{0} t + \frac{a t^{2}}{2}

Ühtlaselt muutuva liikumise liikumisvõrrand

Tegemist on ruutfunktsiooniga, mille liikmed võivad olla sõltuvalt algkoordinaadi, algkiiruse ja kiirenduse märgist nii positiivsed kui ka negatiivsed. Liikme märk sõltub vastava suuruse suunast koordinaattelje suhtes. Märgi olulisuse rõhutamiseks kasutatakse võrrandi üldkujus + asemel mõnikord sümbolit ±. Sel juhul näeb liikumisvõrrand välja veidi teistsugusena:

x = x_{0} \pm v_{0} t \pm \frac{a t^{2}}{2}

Iga konkreetse liikumise korral on võrrandis x₀, v₀ ja a kohal vastavate suuruste arvväärtused.

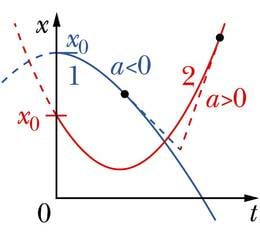
Ühtlaselt muutuva liikumise graafik

Nüüd, mil teame, et ühtlaselt muutuva liikumise liikumisvõrrand (1.19 ) kujutab endast aja ruutfunktsiooni, mis on sarnane matemaatikast tuntud funktsiooniga y = ax²+ bx + c, pole raske konstrueerida ka selle liikumise graafikut.

Koordinaat x sõltub ajast t kui ruutfunktsioon. Ruutfunktsiooni graafik on teatavasti parabool ja nii ongi ühtlaselt muutuva liikumise graafik parabooli kujuga. Sõltuvalt ruutliikme kordaja (kiirenduse) märgist on parabooli harud suunatud kas üles (a > 0) või alla (a < 0).