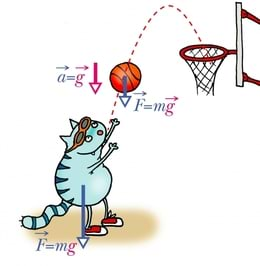Raskusjõud

Meie jaoks on eriline muidugi see gravitatsioonijõud, millega Maa tõmbab kõiki seda ümbritsevaid kehi. Tänu sellele jõule kukuvad kõik kehad alla Maa keskpunkti poole ja on tõstmisel rasked. Tegemist on meile tuttava raskusjõuga. Raskusjõud pole iseloomulik mitte ainult Maale, vaid ilmneb tugevamalt või nõrgemalt kõikidel taevakehadel. Raskusjõuks nimetatakse gravitatsioonijõudu, millega Maa või mis tahes muu taevakeha tõmbab enda poole selle lähedal asuvaid kehi.

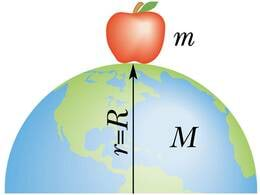
Raskusjõu saame leida gravitatsiooniseadusest (2.11 ). Võttes ühe keha massiks Maa massi M ning vahekauguseks Maa raadiuse R, tuleb maapinnal asuvale kehale massiga m mõjuvaks raskusjõuks

F = G \frac{M m}{R^{2}}

Kui suure kiirenduse see jõud kehale annab? Kasutame Newtoni II seadust (2.2 ):

a = \frac{F}{m} = G \frac{M m}{R^{2} m} = G \frac{M}{R^{2}}

ehk

(2.15)

a = G \frac{M}{R^{2}}

Et Maa mass on 5,98•10²⁴ kg ja raadius 6370 km = 6,37•10⁶ m, annavad arvutused

a = 6, 67 \cdot 10^{- 11} \cdot \frac{5, 98 \cdot 10^{24}}{{(6, 37 \cdot 10^{6})}^{2}} = 9, 83 \approx 9, 8 (\frac{m}{s^{2}})

See kiirenduse väärtus on meile tuttav kui vaba langemise kiirendus. Vaba langemise kiirendust nimetatakse veel raskus- ehk gravitatsiooni-kiirenduseks. Viimasest ongi tulnud tähis g.

Teades nüüd, et vabalt langeva keha kiirendus on $\to g$ , saame Newtoni II seadusest seda kiirendust tekitava jõu ehk raskusjõu arvutamiseks lihtsa valemi:

(2.16)

\to F = m \to g

See raskusjõud on suunatud Maa keskpunkti ega ole seepärast Maakera kõigis punktides samasuunaline.

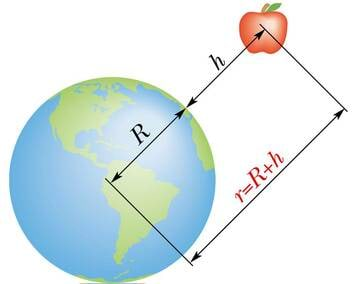
Kõrguse kasvades raskuskiirendus väheneb, sest valemis (2.15 ) tuleb Maa raadiusele liita ka kõrgus maapinnast h:

g = G \frac{M}{{(R + h)}^{2}}


	Kuna Kuu mass on Maa massist palju väiksem, mõjub selle pinnal objektidele ka väiksem raskusjõud.

Kuna raskuskiirenduse vähenemine muutub märgatavaks alles 100 km kõrgusel, mida loetakse kokkuleppeliselt kosmose piiriks, siis on tavaelus mugavam kasutada nn lapiku Maa mudelit (midagi antiikaegse ettekujutuse sarnast). Selle mudeli puhul mõjub kõikidele Maa-lähedastele kehadele vertikaalselt alla suunatud raskusjõud, mis kõrgusest ei sõltu.