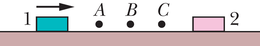Kui mehaanikainsener kutsutakse eksperdiks liiklusõnnetuse põhjuste selgitamisel, tuleb tal kasutada füüsikat. Balletikooli treener, kes õpetab hüpete korrektset sooritamist, kasutab füüsikat. Keeruliste liikumiste uurimisel tuleb teha lihtsustusi, mis eeldavad füüsika tundmist. Selles peatükis vaatame, kuidas keeruliste süsteemide nagu auto või baleriini liikumisi saab lihtsustada, määratledes süsteemis erilise punkti, mida nimetatakse selle süsteemi massikeskmeks.
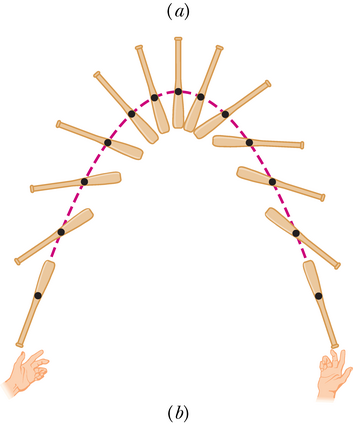
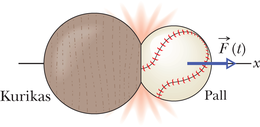
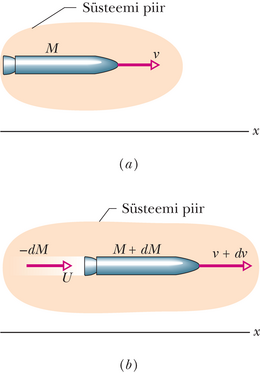
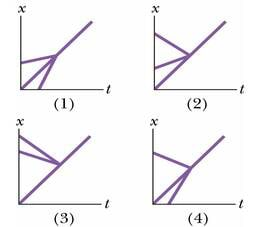
Siin on üks näide. Kui viskate üles palli (joonis 9-1a) seda pöörlema panemata, on liikumine lihtne – pall liigub piki parabooli, nagu me leidsime neljandas peatükis, kus palli käsitleti punktmassina. Kui aga visata üles pesapallikurikas (joonis 9-1b), on selle liikumine keerulisem. Kuna kurika iga osa liigub erinevalt ja piki vägagi erineva kujuga trajektoore, ei saa me teda käsitleda kui punktmassi. Seega on meil tegu punktmasside süsteemiga, kus igaüks neist liigub iseenda teed pidi. Sellel kurikal on aga üks eriline punkt – tema massikese, mis ikkagi liigub lihtsal paraboolsel trajektooril. Kurika ülejäänud punktid liiguvad ümber selle punkti. (Et määrata massikeskme asukoht, pange kurikas väljasirutatud sõrme peal tasakaalu; sõrme kohale jääv kurika sümmeetriateljel asuv punkt ongi tema massikese.)
Pesapallikurika pildumisega te elus edu ei saavuta. Küll aga võite te olla edukas, kui oskate öelda kaugushüppajale või tantsijale, kuidas end õigesti õhku tõugata, kuidas hoida käsi ja jalgu ning millal ja kuidas pöörata oma keha. Ja lähtepunktiks on alati inimese massikese, kuna selle liikumine on kõige lihtsam.
Me defineerime punktmasside süsteemi (näiteks inimese) massikeskme selleks, et saaks ennustada süsteemi liikumist.
Punktmasside süsteemi massikeskmeks on punkt, mis liigub nii, nagu (1) sellesse punkti oleks koondunud kogu süsteemi mass ja (2) sellesse punkti oleks rakendatud kõik süsteemile mõjuvad välisjõud.
Kõigepealt vaatleme, kuidas leida punktmasside süsteemi massikeset. Alustame vähesest arvust punktmassidest koosnevatest süsteemidest ning jõuame väga suurest hulgast punktidest koosnevateni, nagu seda on jäigad kehad (näiteks pesapallikurikas). Seejärel uurime, kuidas liigub massikese süsteemile mõjuvate välisjõudude toimel.
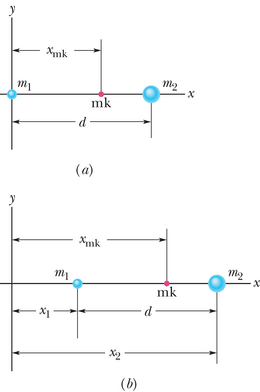
Joonis 9-2a kujutab kahte punktmassi massidega ja , mis asuvad teineteisest kaugusel . Oleme võtnud süsteemi ühe punkti asukohaks koordinaatide alguspunkti ja punkte ühendavaks jooneks -telje. Sellise kahest punktmassist koosneva süsteemi massikeskmeks defineerime punkti
Oletame näiteks, et . Siis jääb süsteemi vaid üks punktmass ja selle asukoht ongi massikese. Seega , nagu see tuleneb valemist 9-1. Kui , on süsteemis jällegi üks punktmass ja, nagu võiski arvata, on massikeskmeks . Kui , asub massikese täpselt punktmasside vahel ja valem 9-1 annab selle asukohaks tõesti . Ja lõpuks, juhul kui me ei tea masside ja väärtusi, võib väärtus olla vahemikus null kuni , teiste sõnadega peab massikese asuma kusagil nende punktmasside vahel.
Joonisel 9-2b näeme veel üldisemat juhtu, kus koordinaatide alguspunkt on nihutatud vasakule. Nüüd defineerime massikeskme asukoha:
Pange tähele, et kui võtame x1=0, siis x2 saab väärtuseks ning valem 9-2 taandub valemiks 9-1 nii, nagu see peabki olema; samuti seda, et vaatamata koordinaatide muutumisele jääb massikeskme kaugus mõlemast punktmassist endiseks.
Valemi 9-2 võime kirjutada kujul
kus M on süsteemi kogumass (). Me võime valemi üldistada juhule, kus piki -telge paikneb punktmassi. Siis on süsteemi kogumass ja massikeskme asukohaks on
Alumine indeks võib omada täisarvulisi väärtusi kuni .
Kui punktmassid paiknevad kolmemõõtmelises ruumis, saab süsteemi massikeskme asukohta väljendada kolme koordinaadiga. Need koordinaadid leiame, üldistades valemit 9-4:
Massikeskme asukohta saab määratleda ka vektorite abil. Kõigepealt tuletame meelde, et punktmassi asukohta väljendavaid koordinaate , ja saab esitada kohavektorina
Siin alumine indeks on punktmassi number, vektorid , ja aga on vastavalt telgede , ja positiivsesse suunda osutavad ühikvektorid. Punktmasside süsteemi massikeskme kohavektori võime kirjutada samal kombel:
Valemi 9-5 kolme skalaarset võrrandit esitab nüüd üksainus vektorvõrrand
kus on jällegi süsteemi kogumass. Te võite seda kontrollida, asendades sellesse valemid 9-6 ja 9-7 ning leides -, - ja -komponendid. Tulemuseks ongi skalaarsed võrrandid 9-5.
Tavalised kehad, nagu näiteks pesapallikurikas, sisaldavad nii palju osakesi (aatomeid), et neid on parem käsitleda kui ühtlase ainejaotusega ruumilisi objekte. Sellisel juhul me vaatleme punktmassina käsitletavaid osakesi kui massielemente , valemiga 9-5 esitatud summa läheb üle integraaliks ning massikeskme koordinaadid defineeritakse kui
kus tähistab nüüd vaadeldava keha massi.
Et enamiku igapäevaelust tuntud kehade (nagu lehm või televiisor) jaoks on sellise integraali leidmine keeruline, räägime siin ainult homogeensetest kehadest. Sellised kehad on ühtlase tihedusega (tihedus väljendab ruumalaühiku massi), see tähendab, nende tihedus (kreeka täht roo) on ühesugune selle keha kõigi ruumielementide jaoks. Valemist 1-8 võime kirjutada
kus on massielemendile dm vastav ruumala ning on keha koguruumala. Asendades valemist 9-10 valemisse 9-9, saame
Te pääsete ühe või enama integraali võtmisest juhul, kui uuritav keha on sümmeetriline mingi punkti, sirge või tasandi suhtes. Sel juhul asub massikese selles punktis, joonel või tasandil. Näiteks ühtlase tihedusega kera (millel on sümmeetriakese) massikese on kera keskpunktis (mis ongi kera sümmeetriakeskmeks). Ühtlase tihedusega koonuse (mille telg on tema sümmeetriateljeks) massikese asub koonuse teljel. Banaan on sümmeetriline tasandi suhtes (see tasand jagab banaani kaheks täpselt ühesuguseks osaks) ja tema massikese asub kusagil sellel tasandil.
Keha massikese ei pea ilmtingimata asuma selle keha sisemuses. Rõngassaia massikeskmes saia ei ole, ei ole ka teragi rauda hobuseraua massikeskmes.
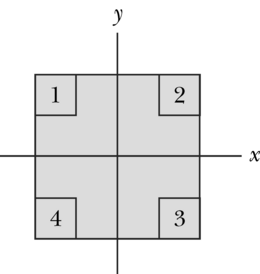
KONTROLLKÜSIMUS 1
Näidisülesanne 9-1
Lahendus
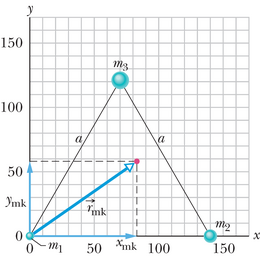
JUHTMÕTE Et tegu on punktmasside, mitte aga ruumilise tahke kehaga, siis tuleb massikeskme asukoha leidmiseks kasutada valemit 9-5. Et kõik punktmassid asuvad kolmnurgaga määratud tasandis, siis on meil vaja ainult kahte esimest võrrandit.
Arvutused: Arvutusi saab lihtsustada, valides - ja -teljed nii, et üks punktmassidest asub koordinaatide alguspunktis ning -telg ühtib kolmnurga ühe küljega (joonis 9-3). Punktmasside koordinaadid on sel juhul
| Punktmassi number | Mass () | () | () |
| 140 | |||
| 3,4 |
Valemi 9-5 abil leiame masskeskme koordinaadid
ja
Joonisel 9-3 osutab massikeskmesse kohavektor komponentidega on ja .
Näidisülesanne 9-2 Arenda oma oskusi
Lahendus
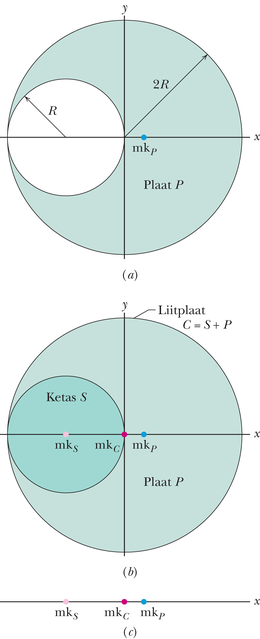
JUHTMÕTTED (1) Püüame kõigepealt hinnata massikeskme ligikaudset asukohta, lähtudes plaadi sümmeetriast. Näeme, et plaat on sümmeetriline -telje suhtes (kui plaati pöörata ümber -telje nii, et alumine ja ülemine pool vahetavad kohad, siis pilt ei muutu). Järelikult asub -teljel. Plaat ei ole aga sümmeetriline -telje suhtes, kuna vasakust poolest on tükk välja lõigatud. Kuna paremal pool telge on massi rohkem, peab ka olema nihutatud -teljest paremale. Seega võime umbkaudse asukoha märkida nii, nagu on joonisel 9-4a.
(2) Plaat on ruumiline jäik keha, järelikult tuleb koordinaatide leidmiseks kasutada valemeid 9-11. See arvutus on otse üsna keeruline. On olemas lihtsam tee: lähtuda massikeskme leidmisel toimivast võttest, kus keha mass on koondatakse tema massikeskmesse.
Arvutused: Kõigepealt paneme väljalõigatud tüki (olgu see plaat ) tagasi oma kohale (joonis 9-4b), saades nii liitketta (olgu see plaat ). Kuna ketas on sümmeetriline oma keskpunkti suhtes, asub tema massikese ta keskpunktis asukohaga (nagu on näidatud joonisel). Samamoodi saame, et liitketta massikese asub tema keskmes, järelikult koordinaatide alguspunktis. Nii saame, et
| Plaat | Massikese | Massikeskme asukoht | Mass |
Kujutleme, et ketta mass on koondatud punktmassiks asukohaga ja mass on koondatud punktmassiks asukohaga (joonis 9-4c). Oletame, et need kaks punktmassi moodustavad süsteemi, mille massikeskme asukoht on leitav valemiga 9-2. Saame:
Plaadi ja plaadi kokkupanemisel saame plaadi . Järelikult peab liitplaadi massikese massikeskme asukoht langema ühte plaadi massikeskmega , mis aga asub koordinaatide alguspunktis; seega . Kui paneme selle võrduse valemisse 9-12 ja lahendame saadud võrrandi suhtes, saame
Masside suhte saame leida plaatide ja pindalade abil, kuna
Seega
Kuivõrd plaat on ühtlane, siis kõigi osade tihedused ja paksused on ühesugused ja nii jääb meil järgi vaid
Juhis 1: Ülesanded massikeskmega
Ülesanded massikeskmega Näidisülesannetes 9-1 ja 9-2 esitasime kolm põhilist massikeskme ülesannete lahendamise võtet. (1) Kasutage maksimaalselt keha sümmeetriaomadusi, olgu see siis sümmeetria punkti, telje või tasandi suhtes. (2) Kui on võimalik keha jagada osadeks, siis käsitlege igaüht neist kui punktmassi asukohaga selle osa massikeskmes. (3) Koordinaate valige targalt: kui süsteem koosneb punktmassidest, pange üks neist koordinaatide alguspunkti. Kui keha on telgsümmeetriaga, pange x- või y-telg piki seda telge. Koordinaatide alguspunkti valik on täiesti meelevaldne, kuna massikeskme asukoht sellest ei sõltu.
Nüüd, kus me teame, kuidas määrata punktmasside süsteemi massikeskme asukohta, võime uurida seda, kuidas liigub massikese süsteemile mõjuvate jõudude toimel. Alustame lihtsa süsteemiga, mis koosneb kahest piljardikuulist.
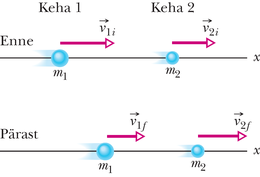
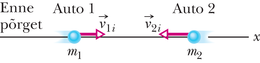
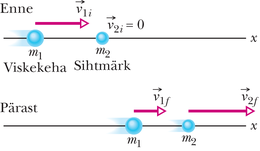
Kui te lööte valge piljardikuuli vastu paigalseisvat kuuli, siis on ju loomulik, et see kahest kuulist koosnev süsteem liigub edasisuunas ka pärast kuulide põrget. Te oleksite väga imestunud, kui mõlemad kuulid hakkaks veerema tagasi teie poole või veereksid koos kas paremale või vasakule poole.
See, mis jätkab liikumist löögi suunas ja mille liikumine põrkegi tõttu üldse ei muutu, on kahest kuulist koosneva süsteemi massikese. Kui te jälgite seda punkti – mis on alati täpselt keskel nende kahe kuuli vahel, kui kuulid on ühesuguste massidega – siis võite selles veenduda piljardilaual toimuvat jälgides. Pole oluline, kas löödud kuul tabab paigalseisvat riivamisi, otse keskele või kuhugi vahepeale, massikese jätkab liikumist otsesuunas nii, nagu poleks põrget olnudki. Uurime seda massikeskme liikumist põhjalikumalt.
Selleks asendame piljardikuulide paari punktmassist koostatud süsteemiga. (Punktmasside massid ei pruugi olla samad.) Meid ei huvita, kuidas igaüks neist liigub, meid huvitab ainult see, kuidas liigub massikese. Ehkki tegu on vaid mõttelise punktiga, peab see liikuma nii, nagu oleks kogu süsteemi mass koondatud sellesse punkti; me saame igal ajal määrata selle punkti asukohta, kiirust ja kiirendust. Me väidame (ja seejärel tõestame), et sellise punktmasside süsteemi massikeskme liikumise vektorvõrrand on
See ongi Newtoni teine seadus punktmasside süsteemi massikeskme liikumise kohta. Märgime, et tema matemaatiline vorm on täpselt sama () kui ühe punktmassi korral. Siiski tuleb selles valemis olevaid kolme suurust väga hoolikalt määratleda.
- ( on kõigi süsteemile mõjuvate välisjõudude resultant. Jõud, millega üks süsteemi kuuluv punktmass mõjutab teist omasugust (süsteemi sisejõud) siin arvesse ei tule.
- on süsteemi kogumass. Me eeldame, et süsteemist ei lahku ega tule juurde mitte mingit massi, nii et kogumass on konstantne. Sellist süsteemi nimetatakse suletud süsteemiks.
- on süsteemi massikeskme kiirendus. Valem 9-14 ei anna meile mitte mingit teavet ükskõik millise sellesse süsteemi kuuluva punktmassi liikumise kohta.
Valem 9-14 on samaväärne kolme võrrandiga, mis seovad vektorite ja koordinaattelgede suunalisi komponente. Need võrrandid on:
Tuleme nüüd tagasi oma ülesande juurde ja uurime piljardikuulide liikumist. Hetkest, kus kiilöök paneb ühe kuuli liikuma, ei mõju meie (kahest kuulist koosnevale) süsteemile enam ükski välisjõud. Seega, kuna , annab valem 9-14, et ka . Kuna kiirendus on kiiruse muutus ajaühikus, võime järeldada, et kahest piljardikuulist koosneva süsteemi massikeskme kiirus ei muutu. Kui kaks kuuli põrkuvad, tulevad mängu sisejõud, millega üks kuul mõjutab teist kuuli. Need jõud ei tule arvesse arvutamisel ja see jääb endiselt nulliks. Seetõttu peab süsteemi massikese, mis liikus otse edasi enne põrget, jätkama samasugust liikumist ka pärast põrget, sama kiirusega ja samas suunas.
Valem 9-14 kehtib mitte üksnes punktmasside süsteemi kohta, vaid ka jäikade kehade korral nagu joonisel 9-1b toodud pesapallikurikas. Valemis 9-14 on siis kurika mass ja kurikale mõjuv gravitatsioonijõud, mis annab . Teiste sõnadega, kurikas liigub nii, nagu oleks ta üksainus punktmass massiga , millele mõjub jõud .
Joonis 9-5 kujutab veel üht huvitavat juhtu. Ilutulestiku ajal lendu saadetud rakett liigub piki parabooli. Selle mingis punktis ta plahvatab. Kui plahvatust poleks olnud, oleks rakett jätkanud oma teed piki joonisel kujutatud trajektoori. Plahvatusel tekkinud jõud on süsteemi suhtes sisejõud (algul oli süsteemiks rakett, pärast moodustavad süsteemi selle killud); see tähendab, et need on jõud, millega süsteemi osad mõjutavad teisi süsteemi osi. Kui õhutakistust mitte arvestada, on ainsaks süsteemile mõjuvaks välisjõuks endiselt gravitatsioonijõud, vaatamata sellele, et rakett on vahepeal purunenud. Seega valemi 9-14 kohaselt jääb süsteemi massikeskme kiirendus endiselt võrdseks -ga. Järelikult jätkab raketikildude massikese liikumist samal trajektooril, millel oleks liikunud rakett siis, kui plahvatust poleks toimunud.
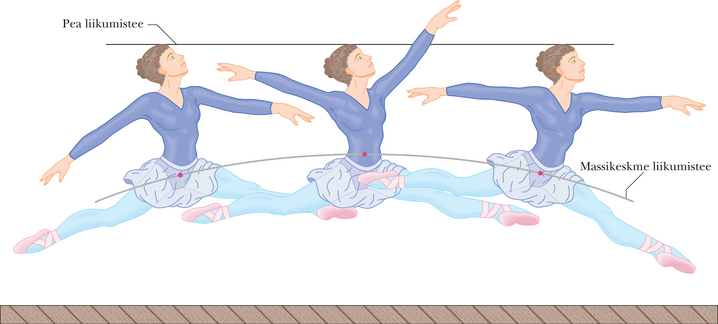
Kui baleriin sooritab hüpet grand jeté, tõstab ta oma käed ja sirutab jalad välja horisontaalasendisse niipea, kui jalad on põrandalt lahti kerkinud (joonis 9-6). Selle liigutusega nihutab ta oma keha massikeset ülespoole. Kuigi ülesnihutatud massikese jätkab endiselt liikumist paraboolsel trajektooril, vähendab massikeskme liikumine keha suhtes pea ja ülakeha kõrgust tavalise hüppega võrreldes. Tulemuseks on see, et pea ja ülakeha liiguvad peaaegu horisontaaljoont pidi, luues sellega illusiooni, nagu hõljuks baleriin lava kohal.
Tõestame nüüd selle tähtsa valemi kehtivuse matemaatiliselt. Valemist 9-8 saame punktmassist koosneva süsteemi jaoks
kus on süsteemi kogumass ja on selle süsteemi massikeskme kohavektor.
Võttes valemist 9-16 tuletise aja järgi, saame
Siin () on -nda punktmassi kiirus ja () on süsteemi massikeskme kiirus.
Võttes valemist 9-17 tuletise aja järgi, saame
Siin () on -nda punktmassi kiirendus ja () on massikeskme kiirendus. Kuigi massikese on kõigest geomeetriline punkt, on tal asukoht, kiirus ja kiirendus täpselt nagu punktmassilgi.
Newtoni teise seaduse kohaselt võrdub -ndale punktmassile mõjuva resultantjõuga . Seega võime valemi 9-18 kirjutada kujul
Valemi 9-19 parem pool sisaldab nii jõudusid, millega üksteist mõjutavad süsteemi kuuluvad punktmassid (sisejõud), kui ka neid jõudusid, millega süsteemi kuuluvaid punktmasse mõjutavad süsteemivälised kehad (välisjõud). Newtoni kolmanda seaduse kohaselt mõjuvad sisejõud paarikaupa ja kuna nad on võrdsed ja vastassuunalised, siis järelikult summeerimisel taanduvad nad võrrandi 9-19 paremast poolest välja. See, mis järele jääb, on kõigile süsteemi kuuluvatele punktmassidele mõjuvate välisjõudude vektorsumma. Nii taandub võrrand 9-19 võrrandiks 9-14, mida me tahtsimegi tõestada.
KONTROLLKÜSIMUS 2
Näidisülesanne 9-3
Lahendus
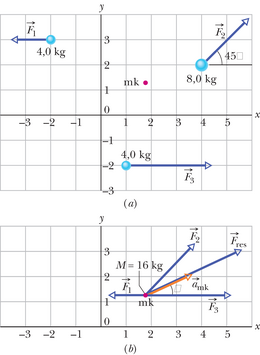
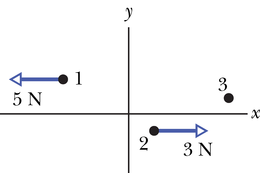
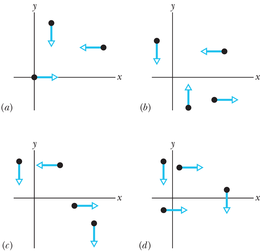
JUHTMÕTTED Süsteemi massikeskme asukoha saame näidisülesandes 9-1 toodud meetodil ning joonisel on see märgitud punktiga. Me võime seda massikeset vaadelda kui punktmassi, kuhu on koondunud süsteemi kogumass . Kolme välisjõudu võime vaadelda nii, nagu mõjuksid nad kõik massikeskmele (joonis 9-7b).
Arvutused: Nüüd saame massikeskmele rakendada Newtoni teist seadust, kirjutades
või
ja seega
Valemist 9-20 näeme, et massikeskme kiirendus on samasuunaline süsteemile mõjuvate välisjõudude resultandiga (joonis 9-7b). Kuivõrd punktmassid seisid alghetkel paigal, siis pidi paigal seisma ka massikese. Kui massikese hakkas liikuma jõu mõjul kiirendusega , siis nende kahe vektori ühises suunas. Võrrandi 9-21 paremat poolt saame arvutada vektorfunktsioonidega kalkulaatoriga, aga võime ka leida võrrandi 9-21 komponentkujust amk komponendid ning siis vektori . Piki -telge saame võrrandi
Selles punktis vaatleme süsteemi asemel ühtainust punktmassi, et defineerida kaks tähtsat suurust. Järgmises punktis 9-5 üldistame neid definitsioone punktmasside süsteemidele.
Esimene definitsioon: punktmassi liikumishulk ehk impulss on vektor , mis defineeritakse seosega
kus on punktmassi mass ja tema kiirus. (Tuleb eristada liikumishulka ehk impulssi ja 11. peatükis sisse toodavat pöörlemishulka ehk pöördeimpulssi.) Kuna on alati positiivne skalaarne suurus, siis valemi 9-22 kohaselt on vektorid ja samasuunalised. Valemist 9-22 leiame ka liikumishulga ühiku SI süsteemis, milleks on kilogramm-meeter sekundi kohta ().
Newton ise formuleeris oma teise seaduse just liikumishulga mõiste abil:
Punktmassi liikumishulga muutumise kiirus on võrdne temale mõjuva kogujõuga ning suunatud selle jõu suunas.
Valemi kujul on see
Valem ütleb, et punktmassile mõjuv välisjõud muudab selle liikumishulka . Kehtib ka vastupidine väide: liikumishulk saab muutuda ainult välisjõu mõjul. Kui välisjõud puuduvad, siis ei muutu. Nagu näeme punktis 9-7, osutub see fakt väga mõjusaks tööriistaks liikumisülesannete lahendamisel.
Asendades valemisse 9-23 avaldise valemist 9-22, saame konstantse massi korral
Seega on valemid ja Newtoni teise seaduse ekvivalentsed formuleeringud punktmassi jaoks.
KONTROLLKÜSIMUS 3
Laiendame liikumishulga definitsiooni punktmasside süsteemile. Vaatleme süsteemi, mis koosneb punktmassist, milledel kõigil on oma mass, kiirus ja liikumishulk. Need punktmassid võivad üksteist mõjutada, samuti võivad neile mõjuda välisjõud. Süsteemi kui terviku liikumishulga võime defineerida kui kõigi süsteemi kuuluvate punktmasside liikumishulkade vektorsumma. Seega
Kui võrrelda seda valemiga 9-17, näeme, et
mis on teine viis süsteemi liikumishulga määratlemiseks.
Kui võtta valemist 9-25 tuletis aja järgi, siis saame
Võrreldes valemeid 9-14 ja 9-26 leiame, et Newtoni teist seadust punktmasside süsteemi jaoks saab kirja panna kujul
kus on süsteemile mõjuvate välisjõudude resultant. See valem üldistab ühe punktmassi kohta käivat seost punktmasside süsteemile. Teiste sõnadega, süsteemile mõjuvad välisjõud muudavad süsteemi liikumishulka. Kehtib ka vastupidine väide: süsteemi liikumishulk saab muutuda vaid siis, kui on olemas välised jõud. Kui välisjõud puuduvad, siis ei saa muutuda.
Punktmassina käsitletava keha liikumishulk ei saa muutuda seni, kuni ükski välisjõud ei sunni seda muutuma. Te võite mingit keha tõugata ning sel teel muuta tema liikumishulka. Või siis võite sundida keha põrkama vastu pesapallikurikat. Sellise põrke korral on välisjõu mõju lühiajaline, kuid tugev, ja keha liikumishulk muutub äkiliselt. Sellised põrked on igapäevaelus sagedased, aga enne, kui nende juurde asuda, vaatleme lihtsat põrget, mille käigus punktmassina käsitletav liikuv viskekeha põrkub mingi teise kehaga (sihtmärgiga).
Olgu liikuvaks kehaks pall, mida lüüakse pesapallikurikaga. Põrge on lühiajaline ja pallile mõjuv jõud piisav, et seda pidurdada, peatada ning sundida liikuma vastassuunas. Joonis 9-8 kujutab seda põrget mingil ajahetkel. Pallile mõjub jõud , mis põrke ajal muutub ning mille tagajärjel muutub palli liikumishulk . Seda muutust seob jõuga Newtoni teine seadus . Palli liikumishulga muutus ajavahemiku dt vältel avaldub valemiga
Me saame leida palli liikumishulga muutuse kogu põrke jooksul, kui integreerime valemit 9-28 põrkele eelnenud ajahetkest kuni ajahetkeni , kus põrge on juba toimunud:
Võrrandi vasak pool annab meile liikumishulga muutuse . Paremat poolt, mille määrab nii põrke kestus kui selle ajal mõjunud jõud, nimetatakse jõuimpulsiks :
Seega on keha liikumishulga muutus võrdne temale mõjunud jõuimpulsiga:
Seda võrrandit saab esitada ka vektorkujul
või nende vektorite komponentide kaudu
ning
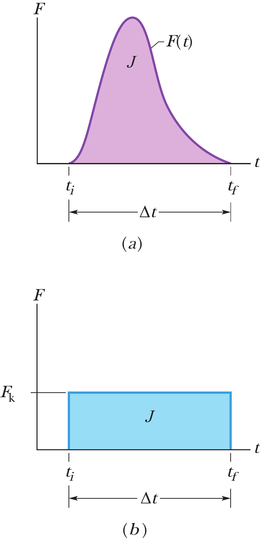
Kui me teame funktsiooni , võime leida (ja koos sellega ka liikumishulga muutuse) selle funktsiooni integreerimise teel. Kui meil on graafik, mis kujutab sõltuvust ajast , siis saame leida kui jõudu kujutava kõvera ja ajatelje vahele jääva pindala nii, nagu seda on tehtud joonisel 9-9a. Tihtipeale me aga ei tea, kuidas muutub jõud ajas, kuid teame keskmise jõu väärtust põrke toimumisaja () vältel. Sellisel juhul võime jõuimpulsi väärtuse kirjutada kujul
Keskmise jõu ja aja vahekorra graafiline esitus on joonisel 9-9b. Sellel oleva ristküliku pindala peab olema võrdne tegeliku kõvera alla jääva pindalaga joonisel 9-9a, kuna mõlemad pindalad on võrdsed jõuimpulsiga J.
Palli asemel võime vaatluse alla võtta joonisel 9-8 oleva kurika. Ükskõik millisel ajahetkel nõuab Newtoni kolmas seadus, et kurikale mõjuv jõud on täpselt niisama suur kui pallile mõjuv jõud, ainult et vastassuunaline. Valemi 9-30 kohaselt tähendab see, et ka kurikale mõjunud jõuimpulss on võrdne ja vastassuunaline pallile mõjunud jõuimpulsiga.
KONTROLLKÜSIMUS 4
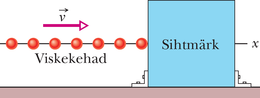
Vaatleme kehale mõjuvat jõudu juhul, kui seda mõjutab terve seeria ühesuguseid ajas korduvaid põrkeid. Näiteks võtame sellise masina, mis suure sagedusega pillub tennisepalle vastu seina. Iga selline põrge mõjutab seina mingi jõuga, aga see pole see jõud, mida me otsime. Me soovime leida seinale sellise pommitamise ajal mõjuvat keskmist jõudu , see tähendab paljude põrgete poolt esile kutsutud jõudude keskmist.
Joonisel 9-10 liigub rida ühesuguse massiga ja ühesuguse liikumishulgaga viskekehasid -telje suunas ning põrkub paigalseisva kehaga. Olgu ajavahemiku jooksul vastu seda keha põrganud viskekehade arv . Et liikumine toimub ühes sihis, võime vektorid asendada nende selle telje suunaliste komponentidega. Sel juhul on iga keha esialgne liikumishulk ja põrke käigus aset leidnud liikumishulga muutus . Liikumishulga summaarne muutus kõigi jooksul vastu paigalseisvat keha põrganud viskekeha kohta on . Sama aja jooksul seinale x-telje suunas mõjunud summaarne jõuimpulss on samuti suurusega , kuid vastassuunaline. Saadud seose võime kirja panna kujul
kus miinusmärk tähendab, et J ja on vastassuunalised.
Teisendades valemit 9-35 ja asendades sinna valemi 9-36, saame leida vaadeldavale kehale põrgete ajal mõjuva keskmise jõu
Selles valemis on keskmine jõud avaldatud põrgete sageduse , viskekehade massi ning kiiruse muutuse kaudu.
Kui viskekehad jäävad pärast põrget seisma, tuleb valemisse 9-37 panna kiiruse muutus kujul
kus () ja () on vastavalt kiirused enne ja pärast põrget. Kui aga viskekehade kiirus pärast põrget on suuruselt sama mis enne, kuid suunalt vastupidine, siis ja me saame
Ajavahemiku vältel on põrkuvate viskekehade kogumass . Seda teades võime valemi 9-37 kirjutada kujul
See valem annab meile keskmise jõu suuruse (uuritava kehaga ajaühikus põrkunud massi) kaudu. Ka siia saame asendada valemist 9-38 või 9-39 sõltuvalt sellest, mis juhtub viskekehadega põrkumise käigus.
KONTROLLKÜSIMUS 5
Oletame, et punktmasside süsteemile mõjuvate välisjõudude resultant (ja koos sellega ka summaarne jõuimpulss) on null (süsteem on isoleeritud) ning et süsteemi moodustavate osakeste arv ei muutu (süsteem on kinnine). Võttes valemis 9-27 , saame, et , ehk
Sõnades öelduna:
Seda järeldust nimetatakse liikumishulga jäävuse seaduseks. Seda võib kirjutada ka kujul
Sõnades öelduna: suletud ja isoleeritud süsteemi korral
Hoiatus: liikumishulka ei tohi segi ajada energiaga. Järgmistes näidisülesannetes jääb muutumatuks liikumishulk, kuid mitte energia.
Valemid 9-42 ja 9-43 on vektorvõrrandid, järelikult on igaüks neist samaväärne kolme võrrandiga, mis kirjeldavad kolme omavahel risti suunatud liikumishulka – teiste sõnadega, liikumishulga -, - ja -komponenti. Sõltuvalt süsteemile mõjuvate välisjõudude iseloomust võib liikumishulk olla mõnikord muutumatu ühes või kahes suunas, kuid mitte kõigis suundades. Täpsemalt:
kui suletud süsteemile mõjuvate välisjõudude resultant on mingi telje suunas null, siis on süsteemi liikumishulga selle telje suunaline komponent muutumatu.
Oletame näiteks, et te viskate apelsini toa teise seina poole. Lennu ajal on ainus apelsinile (mida me vaatleme kui suletud süsteemi) mõjuv välisjõud gravitatsioonijõud, mis on suunatud otse allapoole. Seega muutub küll apelsini vertikaalsuunaline liikumishulk, kuna aga horisontaalsuunalised välisjõud puuduvad, peab liikumishulga horisontaalsuunaline komponent jääma muutumatuks.
Märgime siin, et me vaatlesime üksnes suletud süsteemile mõjuvaid välisjõude. Ehkki süsteemi sisejõud võivad muuta selle süsteemi osade liikumishulki, ei saa nad mõjutada süsteemi kui terviku liikumishulka.
Järgmistes näidisülesannetes toome sisse plahvatused, mis võivad olla ühemõõtmelised (mis tähendab, et kõik liikumised nii enne kui pärast plahvatust toimuvad piki üht telge) või kahemõõtmelised (mis tähendab, et nad liiguvad piki kaht telge omavat tasandit). Edaspidi käsitleme ka ühe- ja kahemõõtmelisi põrkeid.
KONTROLLKÜSIMUS 6
Näidisülesanne 9-4
Lahendus
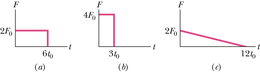
JUHTMÕTTED (1) Jõuimpulss defineeritakse vastavalt valemile 9-30 kui jõu integraal aja järgi (). (2) Keskmine jõud on seotud jõuimpulsi ja jõu toimimisajaga vastavalt valemile 9-35 ().
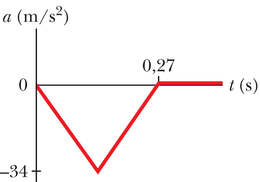
Arvutused: Meil ei ole integreerimiseks vajalikku jõu valemit. Kuid meil on olemas graafik, mis näitab kiirenduse sõltuvust ajast ja millest saame kergesti teha jõu sõltuvuse ajast, korrutades kiirenduse jäära massiga . Nüüd võime integreerida graafiliselt, leides graafiku ja -telje vahele jääva kujundi pindala. Kuna see kujund on kolmnurk, siis saame jõuimpulsi suuruseks
Keskmise jõu väärtuseks saame
Märkus: Jõuimpulss on võrdne jäära liikumishulga muutusega põrke ajal. Seega sõltub jõuimpulsi suurus tema massist ja liikumiskiirusest enne põrget. Et kahevõitlust võita, peab jäär omama võimalikult suurt liikumishulka. Kuid kui jäärade kokkupõrge on kolp vastu kolpa või kolp vastu sarvi, on põrke kestus vaid sellest, mida kasutasime oma arvutustes, ja seetõttu on ka keskmine jõud korda suurem. Nii suur jõud viib teadvuse kaotuseni või isegi surmani; kummalgi juhul pole lootust kahevõitlust jälgiva ute soosingut võita. Jääradel on selle tulemuse vältimiseks painduvad sarved, mis kokkupõrke ajal paindudes pikendavad kokkupõrke kestust ning vähendavad keskmist jõudu umbes njuutonini, mida looma pealuu, aju ja lihased suudavad veel välja kannatada. Kui aga sarv peaks kokkupõrkel purunema, siis võib järgmine kokkupõrge olla saatuslik.
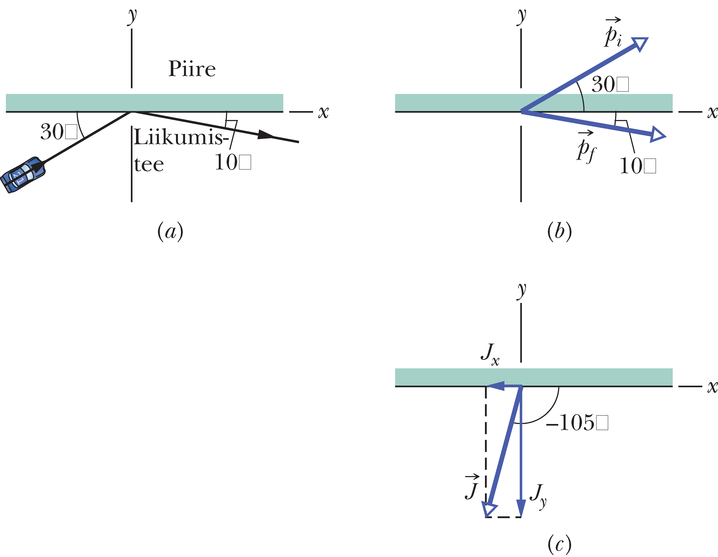
Võidusõiduauto põrkab vastu rajapiiret. Joonisel 9-12a on pealtvaates kujutatud võidusõiduauto juhi teekond auto rajapiirdega põrkamise ajal. Vahetult enne põrget on kiirus suunatud piki piirdega nurga all olevat sirget. Pärast põrget liigub ta kiirusega piki sirgjoont, mille nurk piirdega on . Juhi mass .
(a)
Lahendus
JUHTMÕTTED Me võime autojuhti käsitleda punktmassina, kelle kohta kehtivad ülaltoodud valemid. Seejuures ei saa me arvutamisel kasutada valemit 9-30, kuna me ei tea midagi juhile põrke ajal mõjuva jõu kohta. See tähendab, et meil pole ei funktsiooni ega tema graafikut, mida võiks leidmiseks integreerida. Aga me saame arvutada autojuhi liikumishulga muutumise kaudu valemist 9-32 ().
Arvutused: Joonisel 9-12b on näidatud autojuhi liikumishulga vektor enne põrget (mille nurk -telje positiivse suunaga on ) ja tema liikumishulga vektor pärast põrget (nurk ). Valemitest 9-32 ja 9-22 () saame
Kuna me teame, et , nurga all ja nurga all, võiksime võrrandi parema poole vektorarvutust võimaldava taskuarvutiga kohe välja arvutada. Alljärgnevas kasutame siiski komponentesitust:
Jõuimpulss: Seega jõuimpulss avaldub
kust saame, et jõuimpulsi suurus on
mille väärtuseks annab kalkulaator . Siin tuleb meeles pidada, et sama tangensi annab ka nurk, mis siintoodust võrra erineb. Et teada saada, milline neist on õige, tuleb meil välja joonistada vektori komponendid (joonis 9-12c). Nagu näeme, on õige väärtus , mida võib kirjutada ka kujul
(b)
Lahendus
JUHTMÕTE Valemi 9-35 () kohaselt on keskmine jõud võrdne jõuimpulsi J ja põrke kestuse suhtega.
Arvutused: Me saame
Kasutades valemit ja pannes sinna , leiame, et autojuhi keskmine kiirendus põrke ajal oli ligikaudu . Võib arvata, et selline põrge lõpeb surmaga.
Kuidas ellu jääda: Et suurendada juhi ellujäämise tõenäosust, projekteeritakse võistlusradade piirded pehmemad ja pikendatakse sel teel põrke kestust. Kui ülesandes kirjeldatud põrge kestaks korda kauem ja muud parameetrid jääksid samaks, oleksid nii keskmine jõud kui keskmine kiirendus korda väiksemad ning juhi ellujäämine võrdlemisi tõenäoline.
Näidisülesanne 9-6
Lahendus
JUHTMÕTTED (1) Me saame leida teise tüki kiiruse tema liikumishulgast, kuna teame, et tema mass . (2) Me teame, et kahe tüki liikumishulgad on seotud kasti liikumishulgaga, mis võib olla jääv suurus.
Arvutused: Olgu meie ülesandes taustsüsteemiks põrand. Süsteem, mis koosneb algul ühest kastist ja hiljem kahest tükist, on suletud, aga mitte isoleeritud, kuivõrd nii kastile kui selle tükkidele mõjuvad gravitatsioonijõud ja põranda normaaljõud. Et need jõud mõjuvad vertikaalsihis, ei saa nad muuta süsteemi liikumishulga horisontaalkomponente. Sedasama ei saa teha ka plahvatuse põhjustanud jõud, kuna need on süsteemi sisejõud. Seetõttu on süsteemi liikumishulga horisontaalkomponent jääv ja me saame -telje suunaliste liikumiste puhul kasutada valemit 9-43.
Süsteemi liikumishulk alghetkel on sama mis kastil, Kirjutame samal moel välja tükkide liikumishulgad pärast plahvatust:
Süsteemi lõpp-liikumishulk on tükkide liikumishulkade vektorsumma:
Kuna kõik kiirused ja liikumishulgad on -telje sihis, kirjutame nad -komponentidena ning rakendame neile valemit 9-43, saades
ehk
Pannes siia algandmed, leiame
ja seega
Kuna tulemus on plussmärgiga, liigub ka teine tükk -telje positiivses sihis.
Näidisülesanne 9-7
Lahendus
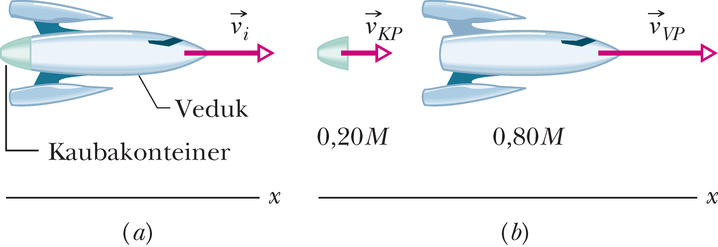
JUHTMÕTE Kuna raketist ja konteinerist koosnev süsteem on suletud ja isoleeritud, on tema liikumishulk jääv, seega
kus indeksid ja viitavad süsteemi olekule enne ja pärast lahtihaakimist.
Arvutused: Kuna liikumised toimuvad piki üht telge, võime nii liikumishulgad kui kiirused kirja panna kui -komponendid ning kasutada suuna määrajana miinusmärki. Enne lahtihaakimist on
Olgu lahtihaagitud konteineri kiirus Päikese suhtes. Siis on kogu süsteemi liikumishulk pärast lahtihaakimist
kus parema poole esimene liige on konteineri liikumishulk ja teine liige käib raketi kohta.
Me ei tea, kui suur on konteineri kiirus Päikese suhtes, aga me saame selle avaldada tuntud suuruste kaudu:
Sümbolite keeles on see
ehk siis
Pannes siia valemist 9-46 ja asetades seejärel valemid 9-45 ning 9-46 valemisse 9-44, saame
mis annab meile
ehk
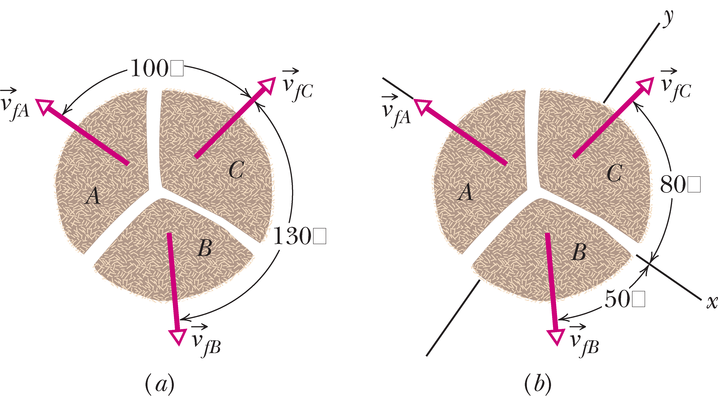
Kahemõõtmeline plahvatus. Kookospähklisse, mille mass on ja mis algselt seisab paigal hõõrdevabal põrandal, on pandud paukhernes. Plahvatades rebib see pähkli kolmeks tükiks, mis libisevad mööda põrandat laiali. Selle sündmuse pealtvaade on joonisel 9-14a. Pärast pauku liigub tükk massiga kiirusega .
(a)
Lahendus
JUHTMÕTE Kõigepealt teeme kindlaks, kas liikumishulk on jääv. Me teame, et (1) pähkel ja selle tükid moodustavad suletud süsteemi, (2) plahvatuse põhjustavad sisejõud ja (3) süsteemile ei mõju välisjõudusid. Järelikult peab liikumishulk olema jääv suurus.
Arvutused: Alustuseks paneme paika -koordinaadistiku nii nagu näidatud joonisel 9-14b, kusjuures -telje negatiivne suund langeb ühte kiiruse suunaga. Sel juhul on nurk -teljega ja nurk sama teljega .
Teame, et liikumishulk on jääv ka telgedele vastavate komponentide jaoks. Võtame näiteks -telje ja saame
kus indeks viitab algväärtustele (enne plahvatust) ja indeks viitab vektorite ja -komponentidele.
Esialgse liikumishulga komponent on null, kuna kookospähkel oli sel ajal paigal. Et saada avaldist, tuleb leida kõigi tükkide liikumishulkade -komponendid. Kasutame valemit 9-22 -komponendi jaoks ():
(Et on null, on määratud meie telgede valikuga.) Valem 9-48 saab nüüd kuju
kust leiame, et
(b)
Lahendus
Arvutused: Kuna liikumishulga jäävus kehtib ka -teljel, siis
kus , kuna kookospähkel seisis alguses paigal. Et saada , peame leidma kõigi tükkide impulsside -komponendid pärast plahvatust. Teades, et tüki a mass on (), saame:
Valemi 9-49 võime nüüd kirjutada kujul
millest leiame, et
Juhis 2: Liikumishulga jäävuse seadus
Kui soovime ülesande lahendamisel kasutada liikumishulga jäävuse seadust, peame kõigepealt olema kindlad, et süsteem on suletud ja isoleeritud. Suletud tähendab, et ükski keha (punktmass) ei ületa süsteemi piire mitte kummaski suunas. Isoleeritud tähendab seda, et süsteemile mõjuvate välisjõudude resultant on null. Kui süsteem ei ole isoleeritud, siis pidage meeles, et liikumishulga jäävus kehtib iga komponendi korral eraldi, kui vastav välisjõu komponent on null. Võib juhtuda, et mõne komponendi jaoks liikumishulga jäävus kehtib ja mõne teise jaoks ei kehti.
Järgnevalt valige süsteemi kaks olekut (mida võib nimetada algolekuks ja lõpp–olekuks) ja pange kirja süsteemi liikumishulga avaldised mõlema oleku kohta. Neid valemeid kirjutades jälgige, millist taustsüsteemi te kasutate, samuti tehke kindlaks, et valemid sisaldaksid kõiki süsteemi kuuluvaid kehi ega sisaldaks ühtki süsteemi mittekuuluvat keha.
Lõpuks pange ja avaldised omavahel võrduma ning leidke saadud võrrandist see, mida oli vaja leida.
Punktis 9-6 vaatlesime kahe punktmassina käsitletava keha põrget, uurides ainult ühe kehaga juhtuvat. Edasi võtsime vaatluse alla kogu süsteemi eeldusel, et see on suletud ja isoleeritud. Punktis 9-7 vaatlesime selliste süsteemide kohta käivat reeglit: süsteemi summaarne liikumishulk ei saa muutuda, kuna pole välisjõude, mis seda muudaksid. See on väga oluline reegel, kuna võimaldab määrata põrke tagajärgi ilma põrke kohta käivaid üksikasju (näiteks põrkel tekkivaid vigastusi) teadmata.
Me võime uurida ka kahest põrkuvast kehast koosneva süsteemi kineetilist energiat. Kui see põrke käigus ei muutu, räägime kineetilise energia jäävusest (energia pärast põrget on niisama suur, kui oli enne põrget). Selliseid põrkeid nimetatakse elastseteks põrgeteks. Igapäevaelus aset leidvad põrked nagu kahe auto põrge või siis palli ja kurika põrge toovad alati kaasa mingi energiahulga muutumise kineetilisest energiast mõneks teiseks energialiigiks nagu soojusenergia või hääle energia. Sel juhul süsteemi kineetiline energia ei ole jääv. Selliseid põrkeid nimetatakse mitteelastseteks põrgeteks.
Siiski esineb olukordi, kus me võime lugeda tavaliste kehade põrke ligikaudu elastseks. Oletame, et te lasete põrkepalli kukkuda kõvale põrandale. Kui palli ja põranda (või maapinna) vaheline põrge oleks elastne, siis ei kaotaks pall oma kineetilist energiat ja kerkiks pärast põrget endisele kõrgusele. Tavaliselt on see kõrgus siiski mõnevõrra väiksem kui langemiskõrgus, mis näitab kineetilise energia kaotsiminekut põrkeprotsessi käigus; seega on ka see põrge teatud ulatuses mitteelastne. Sellele vaatamata võime otsustada selle väikese muutuse jätta tähelepanuta ning võtta palli liikumise kirjeldamisel aluseks elastse põrke.
Kahe keha mitteelastsel põrkel kaotab süsteem alati kineetilist energiat. See energiakadu on suurim juhul, kui põrkunud kehad kleepuvad kokku, ja siis on meil tegu täielikult mitteelastse põrkega. Pesapalli ja kurika põrge on mitteelastne. Kui aga pall on märjast kitist ja kleepub kurika külge, siis on põrge täielikult mitteelastne.
Joonis 9-15 kujutab kahte keha enne ja pärast ühemõõtmelist põrget. Näidatud on kehade kiirused enne (indeks ) ja pärast (indeks ) põrget. Need kaks keha moodustavad süsteemi, mis on suletud ja isoleeritud. Sellise süsteemi jaoks võime kirja panna liikumishulga jäävuse seaduse
Kasutades sümboleid, saame
Kuna liikumine on ühemõõtmeline, võime vektorimärgid ära jätta ja vaadelda ainult teljesihilisi komponente, mille suuna määrab märk. Teades, et , võime valemi 9-50 kirjutada kujul
Kui meile on näiteks teada kehade massid ja algkiirused ning ühe keha lõppkiirus, siis võime teise keha lõppkiiruse avaldada valemist 9-51.
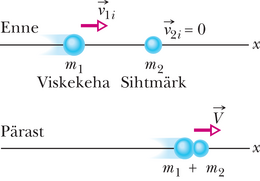
Joonisel 9-16 näeme kahte keha enne ja pärast täielikult mitteelastset põrget (mille käigus nad on kokku kleepunud). Keha massiga oli enne põrget paigal (). Seda keha võime nimetada sihtmärgiks ning liikuvat keha viskekehaks. Pärast põrget liiguvad kokkukleepunud kehad kiirusega . Sellistel tingimustel saab valem 9-51 kuju
ehk
Kui on teada näiteks kehade massid ja viskekeha algkiirus , saame valemi 9-53 abil leida lõppkiiruse . Märgime, et peab olema väiksem kui , kuivõrd masside suhe on ühest väiksem.
Suletud isoleeritud süsteemi massikeskme kiirus ei saa põrke käigus muutuda, kuna isoleeritud süsteemi kehadele ei mõju välisjõudusid, mis võiksid seda muuta. Et saada valemit vmk jaoks, vaatame uuesti joonisel 9-15 kujutatud kahe-keha-süsteemi ühemõõtmelist põrget. Valemi 9-25 () abil saame avaldada selle kahest kehast koosneva süsteemi liikumishulga kaudu, kirjutades
Süsteemi summaarne liikumishulk on põrke käigus jääv ja see kehtib võrrandi 9-50 mõlema poole kohta. Lähtuvalt vasakust poolest võime kirjutada
Pannes siit avaldise valemisse 9-54 ja avaldades sellest , saame
Selle valemi parem pool on konstantne, seega ka väärtus on enne ja pärast põrget ühesugune.
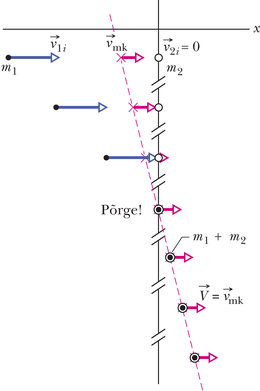
Joonisel 9-17 on näitena toodud seeria stoppkaadreid massikeskme liikumisest joonisel 9-16 kujutatud täielikult mitteelastse põrke jooksul. Keha on sihtmärk ja tema esialgne liikumishulk valemis 9-56 on . Viskekeha esialgne liikumishulk on . Märgime, et sellel stoppkaadrite seerial on näha liikumine nii enne kui ka pärast põrget ja massikese liigub kogu aeg ühesuguse kiirusega vasakult paremale. Pärast põrget langeb kokkukleepunud kehade lõppkiirus ühte massikeskme liikumiskiirusega , kuna siis liigub massikese koos tekkinud liitkehaga.
KONTROLLKÜSIMUS 7
Näidisülesanne 9-9 Arenda oma oskusi
Lahendus
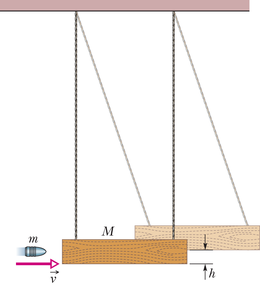
On selge, et klotsi kerkimise kõrgusele määrab kuuli kiirus . Aga me ei saa kasutada nende kahe suuruse vahelise seose leidmiseks energia jäävuse seadust, kuna kuuli puidu sisse tungimise käigus pidi osa tema kineetilisest energiast muutuma teisteks energialiikideks (nagu soojus või puidu lõhkumisel tehtud töö). Me võime selle keerulise liikumise aga jagada kaheks etapiks: (1) kuuli põrge klotsiga ja (2) kuulist ja klotsist koosneva liitkeha võnkumine, mille käigus mehaaniline energia jääb samaks.
Esimene etapp: Kuivõrd kuuli ja klotsi põrge on lühiajaline, võime teha kaks oletust: (1) põrke ajal on klotsile mõjuv gravitatsioonijõud ja nööride pinge tasakaalus. Seetõttu on põrke ajal süsteemile kuul–klots mõjuv väline jõuimpulss null, süsteem on isoleeritud ja tema summaarne liikumishulk jääv. (2) Põrge on ühemõõtmeline selles mõttes, et kuulist ja klotsist koosneva liitkeha liikumissuund vahetult pärast põrget langeb ühte kuuli esialgse liikumissuunaga.
Kuna põrge oli ühemõõtmeline ja klots seisis paigal seni, kuni temasse tungis kuul, siis on liikumishulga jäävuse seadus siin väljendatav valemiga 9-53. Asetades sellesse ülalkasutatud tähised, saame
Teine etapp: Kuivõrd pärast põrget võngub kuul koos klotsiga ülespoole, on süsteemi kuul–klots–Maa mehaaniline energia muutumatu. (Klotsile riputusnööride poolt mõjuv jõud tööd ei tee, kuna ta on kogu aeg risti klotsi liikumissuunaga; järelikult ei muuda ta ka süsteemi mehaanilist energiat.) Võtame klotsi algasendi tugitasandiks, kus loeme gravitatsiooni potentsiaalse energia nulliks. Nüüd tähendab süsteemi mehaanilise energia muutumatus seda, et süsteemi kineetiline energia võnke alguses peab olema võrdne süsteemi potentsiaalse energiaga võnke kõrgeimas punktis. Kuivõrd kuuli ja klotsi kiirus võnke algul on sama mis nende kiirus vahetult pärast põrget, võime energia jäävuse kirja panna kujul
Etapid koos võetuna: Pannes saadud valemisse valemist 9-57 saame
Ballistilise pendli põhimõte on selles, et ta võimaldab teisendada kerge keha (kuuli) suure kiiruse raskema keha (klotsi) väiksemaks ja seetõttu kergemini mõõdetavaks kiiruseks.
Kõige ohtlikumaks liiklusõnnetuseks loetakse autode laupkokkupõrget. Üllatav on seejuures asjaolu, et statistiliselt on autojuhi risk surma saada väiksem juhul, kui tal on kaassõitja. Püüame selgitada, miks.
Joonis 9-19 kujutab kahe ühesuguse auto laupkokkupõrget kui ühemõõtmelist täielikult mitteelastset põrget piki -telge. Kogu kokkupõrke vältel moodustavad autod suletud süsteemi. Lähtume suhteliselt tõepärasest eeldusest, et autodele mõjuv põrkest tingitud jõuimpulss on nii suur, et me võime jätta arvestamata väiksemad jõuimpulsid, mis on seotud rehvide hõõrdumisega teekatte vastu. Nii oletame, et kahest autost moodustatud süsteemile ei mõju välisjõud.
Esimese auto algkiiruse -komponent piki -telge on ja teisel autol . Põrke ajal autodele mõjuvad jõud (ja nende jõuimpulsid) muudavad autode kiirust võrra. Juhi hukkumise tõenäosus sõltub tema auto -st. Me peame välja arvutama kummagi auto kiiruse muutused ja .
(a)
Lahendus
JUHTMÕTE Kuivõrd tegu on suletud ja isoleeritud süsteemiga, siis peab selle summaarne liikumishulk olema jääv.
Arvutused: Valemist 9-51 saame, et
Kuna põrge on täielikult mitteelastne, siis autod ühinevad liitkehaks, mille kiirus pärast põrget on . Asendades valemis 9-58 nii kui lõppkiirusega , saame
Pannes siia algandmed, saame tulemuseks
Seega on esimese auto kiiruse muutus
Ja teise auto kiiruse muutus
(c)
Lahendus
Arvutused: Kirjutame kõigepealt valemi 9-58 ümber kujul
Asendades siia ning , leiame, et
Autojuhi riskifaktor sõltub tema kiiruse muutusest . Valemist 9-61 näeme, et väärtuste suhe on pöördvõrdeline masside suhtega ning see ongi põhjus, miks uurijad on riskifaktori valemis 9-60 seostanud masside suhtega.
Lähtudes osast (a) ja valemist 9-60 ilma kaasreisijata, on esimese autojuhi riskifaktor
Osast (b) ja valemist 9-60 koos kaasreisijaga on esimese autojuhi riskifaktor
Asendades siin c valemist 9-62, saame
Sõnades väljendatuna: autojuhi risk surma saada on võrra väiksem, kui ta autos on kaasreisija.
Nagu mainisime punktis 9-8, on tavaolukorras ette tulevad põrked mitteelastsed; siiski võime mõningatel juhtudel lugeda neid ligikaudu elastseteks. Sellistel juhtudel põrkuvate kehade kineetiline energia säilib ega muutu teisteks energialiikideks:
See ei tähenda, et muutumatuks jääb kõigi kehade kineetiline energia. Pigem tähendab see, et
elastsete põrgete käigus võib iga üksiku keha kineetiline energia muutuda, aga süsteemi kineetiline koguenergia jääb samaks.
Näiteks võib kiiga löödud piljardikuuli põrkumist löödava kuuliga vaadelda kui ligikaudu elastset põrget. Kui tegu on otsepõrkega (löödud kuul liigub täpselt löödava kuuli poole), läheb löödud kuuli kineetiline energia peaaegu tervenisti üle löödavale kuulile. (Fakt, et me kuuleme põrke ajal plaksatust, näitab, et vähemalt mingi osa kineetilisest energiast muutub helienergiaks.)
Joonis 9-20 kujutab kahte keha enne ja pärast ühemõõtmelist otsepõrget, nagu seda oli ülalkirjeldatud piljardikuulide põrge. Liikuva keha mass olgu ja tema kiirus , suunatud otse sihtmärgiks oleva keha poole, mille mass on ja mis seisab paigal (). Eeldame, et see kahe keha süsteem on suletud ja isoleeritud. Sellisel juhul süsteemi liikumishulk põrkel ei muutu ja valemi 9-51 alusel võime seda kirjutada kui
Kuna põrge on elastne, siis säilib ka summaarne kineetiline energia ja me võime kirjutada
Kõigis neis valemites viitab indeks kehade algkiirustele ja indeks lõppkiirustele. Kui me teame kehade masse ja keha algkiirust , siis jäävad ainsateks tundmatuteks ja – kehade lõppkiirused. Kuna meie käsutuses on kaks võrrandit, saame need kaks tundmatut leida.
Et seda teha, kirjutame valemi 9-63 kujul
ja valemi 9-64 kujul*
Jagame need võrrandid omavahel ja pärast algebralisi teisendusi saame
ning
Märgime, et valemis 9-68 on alati positiivne (algselt paigal seisnud keha massiga hakkab alati liikuma ettepoole). Valemist 9-67 näeme, et kiirus võib olla mõlema märgiga (keha massiga m1 hakkab liikuma ettepoole juhul, kui , ja põrkub tagasi juhul, kui ).
Vaatleme mõningaid erijuhte.
- Massid on võrdsed. Kui , siis viivad võrrandid 9-67 ja 9-68 tulemusele mida võib nimetada ka piljardisituatsiooniks. See ennustab, et pärast võrdsete massidega kehade otsepõrget keha (mis algselt liikus) jääb paigale ning keha (mis algselt seisis paigal) hakkab liikuma keha algkiirusega. Otsepõrkel vahetavad võrdse massiga kehad oma kiirused. See on õige ka siis, kui keha ei ole enne põrget paigal.
- Massiivne sihtmärk. Joonisel 9-20 tähendab massiivne sihtmärk fakti, et . Näiteks võime lüüa golfipalli vastu paigalseisvat suurtükikuuli. Valemid 9-67 ja 9-68 annavad sel juhul See tähendab, et keha 1 (golfipall) põrkub tagasi, tema kiirus jääb seejuures peaaegu endiseks. Algselt paigal seisnud keha 2 (suurtükikuul) hakkab edasi liikuma, aga väga väikese kiirusega, kuna valemi 9-69 sulgudes olev liige on väga palju väiksem kui üks. See kõik on ootuspärane.
- Massiivne viskekeha. See on eelmise vastandjuht: . Nüüd lööme suurtükikuuliga paigalseisvat golfipalli. Valemid 9-67 ja 9-68 annavad Valem 9-70 ütleb, et keha (suurtükikuul) jätkab pärast põrget liikumist esialgsest vaid pisut väiksema kiirusega. Keha (golfipall) aga sööstab ettepoole suurtükikuulist kaks korda suurema kiirusega.
Te võite imestada: miks kiirus kahekordistus? Asja üle järele mõtlemist alustades tuletame meelde valemiga 9-69 kirjeldatud juhtu, kus väikese massiga keha (golfipalli) kiirus muutus vahemikus kuni , seega oli muutuse väärtuseks . Täpselt niisama suur kiiruse muutus (aga nüüd nullist kuni ) toimus ka viimases näites.
Seni oleme uurinud viskekeha elastset põrget paigalseisva sihtmärgiga, nüüd asume vaatlema juhtu, kus mõlemad kehad enne põrkumist liiguvad.
Joonisel 9-21 kujutatud olukorras tuleks liikumishulga jäävuse seadus kirjutada kujul
ja kineetilise energia jäävus kujul
Selleks et leida neist võrranditest ja , teisendame kõigepealt valemit 9-71,
ja seejärel valemit 9-72:
Jagades saadud võrrandid omavahel, saame pärast mõningaid algebralisi teisendusi:
ja
Märgime, et sel korral on indeksite omistamine vaadeldavatele kehadele meelevaldne. Kui vahetaksime joonisel 9-20 ning valemites 9-75 ja 9-76 kehade indeksid, jõuaksime ikkagi samasugusele tulemusele. Veel märgime, et kui võtta , siis muutub keha 2 paigalseisvaks sihtmärgiks, nagu on kujutatud joonisel 9-20; valemid 9-75 ja 9-76 aga taanduvad valemiteks 9-67 ja 9-68.
KONTROLLKÜSIMUS 8
Näidisülesanne 9-11
Lahendus
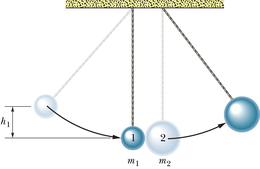
JUHTMÕTE Me jagame selle keerulise liikumise kaheks etapiks ja analüüsime neid eraldi: (1) kera laskumine, (mille käigus säilib mehaaniline energia) ja (2) kerade põrge (mille käigus säilib liikumishulk).
1. etapp: Kui kera liigub allapoole, peab süsteemi kera–Maa mehaaniline energia säilima. (Nööri poolt kerale mõjuv jõud ei saa mehaanilist energiat muuta, kuivõrd ta mõjub risti kera liikumissuunaga ning tema töö on null.)
Arvutused: Võtame süsteemi tugiolekuks kera nr madalaima asendi ja loeme tema gravitatsiooni potentsiaalse energia nulliks. Sellisel juhul peab selle kera kineetiline energia madalaimas asendis olema võrdne süsteemi gravitatsiooni potentsiaalse energiaga hetkel, kui kera on oma kõrgeimas asendis . Seega
mida lahendades leiame kera kiiruse vahetult enne põrget,
2. etapp: Lisaks oletusele, et põrge on elastne, peame siin tegema veel kaks oletust. Esiteks peame oletama, et põrge on ühemõõtmeline, kuna kerade liikumine on ligikaudu horisontaalne nii vahetult enne kui vahetult pärast põrget. Teiseks, kuna põrge kestab väga lühikest aega, oletame, et süsteem on suletud ja isoleeritud. Seetõttu peab süsteemi kogu liikumishulk olema jääv suurus.
Arvutused: Arvestades eelöeldut, võime kera kiiruse leidmiseks vahetult pärast põrget kasutada valemit 9-67:
Miinusmärk tähendab, et kera liigub vahetult pärast põrget vasakule poole.
Kui kaks keha põrkuvad, määrab nende vaheline jõuimpulss ka selle, mis suunas kehad pärast põrget liikuma hakkavad. Juhul kui tegu ei ole otsepõrkega, ei jätka kehad liikumist samas sihis, mis enne põrget. Kui niisugune põrge toimub suletud ja isoleeritud süsteemis, peab aga summaarne liikumishulk jääma endiseks:
Erijuhul, kui on tegu elastse põrkega, jääb muutumatuks ka süsteemi kineetiline energia:
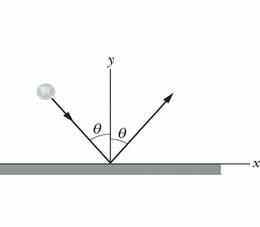
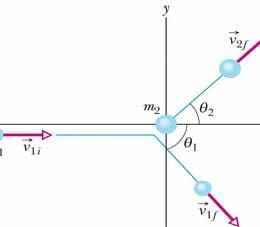
Valemit 9-77 on kahemõõtmelise põrke uurimisel kergem kasutada, kui me kirjutame ta lahti -komponentidena. Joonisel 9-23 on näitena toodud nn riivav põrge (see tähendab, et tegu ei ole otsepõrkega), kus viskekeha tabab paigalseisvat sihtmärki. Põrkel jaguneb liikumishulk nii, et kehad paisatakse laiali suundades, mis moodustavad esialgse liikumissuuna ehk -teljega nurgad θ1 ja θ2. Sellisel juhul võime kirjutada valemi 9-77 liikumishulga -telje suunaliste komponentide jaoks kujul
Samuti võime (erijuhul, kui põrge on elastne) kirjutada valemi 9-78 ümber kiiruste kaudu:
Kolm võrrandit 9-79 kuni 9-81 sisaldavad seitset muutujat: masse ja ; kolme kiirust , ja ning kaht nurka θ1 ja θ2. Kui neist neli on teada, saame leida kolm ülejäänut, lahendades viimasest kolmest võrrandist koosneva süsteemi.
KONTROLLKÜSIMUS 9
Siiani on meil tegu olnud süsteemidega, mille kogumass on jäänud muutumatuks. Mõningatel juhtudel, nagu näiteks raketi korral, ei ole see õige. Stardiseadmel seisva raketi massist moodustab suure osa kütus, mis kõik ära põletatakse ja rakettmootori düüsidest välja paisatakse.
Me käsitleme raketi massi muutumist kiirendamise käigus, rakendades Newtoni teist seadust mitte ainult raketile, vaid raketile koos düüsist välja paisatud põlemisgaasidega. Sellise süsteemi mass ei muutu raketi kiirendamise käigus.
Oletame, et jälgime raketi kiirendamist avakosmoses, kus talle ei mõju ei gravitatsioonijõud ega õhutakistus, sellisest inertsiaalsüsteemist, mille suhtes me ise oleme paigal. Liikumine olgu ühemõõtmeline ning mingil suvalisel ajahetkel olgu raketi mass ja tema kiirus (joonis 9-24a).
Joonis 9-24b kujutab asjade seisu pärast ajavahemiku möödumist. Raketi kiirus on nüüd ja tema mass , kus massi muutus on negatiivne suurus. Olgu raketist ajavahemiku jooksul väljapaisatud gaaside mass ja nende kiirus meie inertsiaalsüsteemi suhtes .
Süsteem, mida uurime, koosneb raketist ja ajavahemiku jooksul välja paisatud gaasidest. Süsteem on suletud ja isoleeritud, seega ei saa tema summaarne liikumishulk selle ajavahemiku jooksul muutuda; niisiis
kus indeksid ja viitavad muutuja väärtustele ajavahemiku algul ja lõpus. Kirjutame valemi 9-82 ümber kujul
kus parema poole esimene liige on aja jooksul väljapaisatud põlemisgaaside liikumishulk ja teine liige raketi liikumishulk pärast ajavahemiku möödumist.
Valemit 9-83 saab lihtsustada, kasutades väljalaskegaaside ja raketi suhtelist kiirust , mida saab arvutada taustsüsteemi suhtes mõõdetud kiiruste kaudu:
Sümbolites kirjapanduna on see
ehk
Pannes siit leitud avaldise valemisse 9-83 ning tehes mõned algebralised teisendused, saame
Asendame nüüd (raketi massi vähenemise kiirus) suurusega , kus on (positiivne) raketi kütusetarve (väljapaisatud gaasihulga massi kasvukiirus), ja tõdeme, et dv/dt ongi raketi kiirendus. Pärast neid asendusi saame:
Valem 9-87 kehtib igal suvalisel ajahetkel, kusjuures mass , kütuse põlemiskiirus ja kiirendus on vastavate suuruste väärtused sellel ajahetkel.
Märgime, et valemi 9-87 vasakul poolel oleva suuruse mõõtühikuks on jõuühik () ja see sõltub üksnes raketi mootori omadustest – nimelt gaaside väljavoolukiirusest ning nende liikumiskiirusest raketi suhtes . Korrutist nimetatakse rakettmootori veojõuks ja tähistatakse tähega . Kui kirjutame , siis näeme selgesti, et tegu on Newtoni teise seadusega, kus on raketi kiirendus hetkel, kui tema mass on .
Kuidas siis leida raketi kiirust sõltuvalt kütuse hulga kahanemisest? Valemist 9-85 saame
Integreerime seda avaldist:
kus on raketi algmass ja tema lõppmass. Integreerimise tulemusena saame
mis annab raketi kiiruse suurenemise selle aja jooksul, kus tema mass muutub väärtusest väärtuseni . (Sümbol „” valemis 9-88 tähendab naturaallogaritmi.) Me võime seda edasi arendada mitmeastmelistele liitrakettidele, kus vähendatakse raketi astmete äraviskamise teel pärast seda, kui nende kütus on lõppenud. Ideaalsel juhul viib rakett sihtkohta üksnes kasuliku koorma.
Rakett algmassiga kulutab kütust kiirusega . Mootori väljalaskegaaside kiirus raketi suhtes, , on .
(b)
Lahendus
JUHTMÕTE Me saame siduda rakettmootori veojõu tema poolt raketile antava kiirendusega ja raketi massiga valemi abil. Kütuse kulutamise käigus raketi mass väheneb ja vastavalt suureneb kiirendus. Kuna meil on vaja leida algkiirendus, peame raketi massi võtma võrdseks algmassiga .
Arvutused: Näeme, et
Kui rakett stardib maapinnalt, peab tema algkiirendus olema suurem kui g=9,8m/s2. Teiste sõnadega peab tema mootori veojõud olema suurem raketile mõjuvast gravitatsioonijõust, mille suuruseks on , mis käesoleval juhul teeb , ehk . Kuivõrd ei kiirenduse ega veojõu nõue pole siin täidetud (), siis ei saa meie rakett maapinnalt iseseisvalt startida. Selleks vajaksime teist, võimsamat raketti.
Ühemõõtmeline mitteelastne põrge
Kui toimub kahe keha mitteelastne põrge, siis sellise kahest kehast koosneva süsteemi kineetiline energia ei säili. Kui süsteem on suletud ja isoleeritud, siis peab süsteemi liikumishulk säilima ja seda saab vektorkujul kirjutada järgnevalt:<
Ühemõõtmeline elastne põrge
Elastseks põrkeks nimetatakse selliseid põrkeid, mille käigus põrkuvatest kehadest moodustatud süsteemi kineetiline energia säilib. Kui see süsteem on suletud ja isoleeritud, siis säilib ka süsteemi liikumishulk. Ühemõõ