Mõõdame näiteks, kui kõrgele põrkub üles tagasi ühe meetri (100 cm) kõrguselt lauale kukkuv pingpongipall. Pärast paari esialgset proovikatset, mis annavad oluliselt erinevaid tulemusi, veendume, et tegemist on A-tüüpi määramatusega. Eelmisest punktist teame, et sellisel juhul tuleb statistiliselt töödelda suurt arvu mõõtmisi. Kui proovikatsed annaksid ühesuguseid tulemusi, võiksime edasises A-tüüpi määramatuse hindamisest loobuda ning asuda B-tüüpi määramatust hindama.

Võtame mõõtmiste arvuks n = 100. Need mõõtmised on ka reaalselt läbi tehtud ja tulemusteks on saadud järgmised sada arvu, mõõtühikutes cm: 69, 75, 73, 72, 70, 72, 73, 72, 70, 75, 70, 74, 74, 75, 74, 76, 71, 70, 69, 77, 74, 69, 70, 75, 72, 75, 71, 72, 73, 69, 73, 71, 74, 73, 77, 72, 71, 73, 74, 74, 71, 72, 72, 72, 72, 74, 72, 73, 71, 71, 73, 74, 70, 70, 74, 73, 72, 71, 73, 76, 73, 71, 71, 68, 70, 73, 72, 71, 72, 72, 73, 72, 74, 70, 73, 71, 72, 72, 72, 74, 72, 73, 71, 73, 71, 75, 74, 75, 73, 71, 75, 73, 76, 74, 73, 72, 74, 72, 71, 73. 

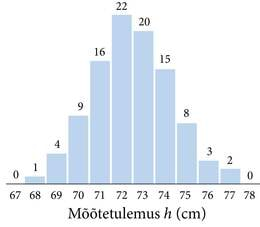
Kui neid arve uurima hakata, siis võib täheldada, et samad mõõtetulemused korduvad aeg-ajalt, kuid mitte ühesuguse sagedusega. Kui 68 cm kõrgusele on pall põrganud vaid ühel ja 77 cm kõrgusele kahel korral, siis 72 cm kõrgusele tervelt 22 korda. Võib oletada, et tulemus, mis sagedamini kordub, on õigem. Matemaatilise statistika teooria kinnitab seda oletust. Juhuslikel põhjustel hajuvate väärtustega suuruse mõõtmisel on mõõtesuuruse tõelise väärtuse parimaks hinnanguks keskväärtus ehk paljude mõõtetulemuste aritmeetiline keskmine (p.2.4.2). Aritmeetiline keskmine leitakse teatavasti kõikide tulemuste summa jagamisel tulemuste arvuga (valem 2.3). Meie saja mõõtetulemuse aritmeetiline keskmine on 72,46 cm. Näeme, et enamik mõõtetulemustest on tõepoolest selle keskmise lähedal. 

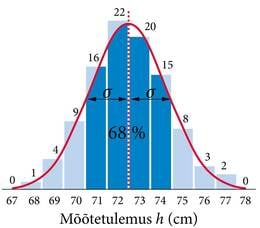
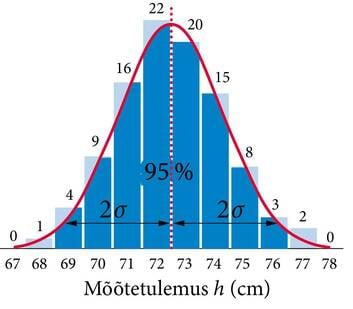
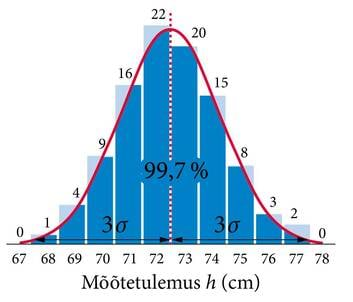
Uurime nüüd, kuidas meie mõõtmiste tulemused on jaotunud (joonis 2.3). Loeme kokku, kui mitu korda on saadud iga erinevat sentimeetrite arvu ning koostame vastava tulpdiagrammi. Sellist diagrammi nimetatakse mõõtetulemuste jaotumise histogrammiks. Näeme, et tulemuste jaotumise histogramm on üsna sümmeetriline. Paigutades histogrammile tulemuste keskmist tähistava joone, näeme, et see jagab histogrammi tõesti keskelt pooleks. Kui teeksime väga palju mõõtmisi ning paigutaksime mõõdiseid histogrammil üha kitsamatesse tulpadesse, siis saaksime tulpade tippude ühendamisel sujuva joone, mida nimetatakse jaotuskõveraks. Jaotuskõvera laius näitab mõõte­määramatust. Puhtjuhuslikult hajuvate mõõdiste jaotuskõvera laiust iseloomustab teatavasti üksikmõõtmise standardhälve σ, mille arvutamise eeskirjaga tutvusime eelmises punktis. Teatavasti me ei pea oskama ise selle eeskirja järgi arvutada. Me kasutame arvutit. Sisestame vastavasse kalkulaatorisse oma katseandmed ja saame teada, et meie katses σ = 1,83 cm. Veendume selles, et keskväärtusest ühe standardhälbe võrra vasakule ja paremale tõmmatud vertikaaljoonte vahele jääb histogrammil tõepoolest ligikaudu 68% kõigist tulemustest (68% kõigi tulpade kogupindalast). Laiendades selliste vertikaaljoonte vahele jäävat vahemikku kummalegi poole keskväärtust kuni kahe standardhälbeni, näeme et vahemikku satub juba ligikaudu 95% kõigist tulemustest. Keskväärtusest kolme standardhälbe (ca 5,5 cm) võrra kummalegi poole ulatuv vahemik (67 cm kuni 78 cm) hõlmab aga juba kõik tulemused (100%, teoreetiline väärtus 99,7%). 

Meie konkreetsel juhul tuleb arvestada, et üksikmõõtmised on tehtud täpsusega 1 cm. Ümardame ära tõenäosusega 95% kehtiva mõõtemääramatuse hinnangu 2σ = 3,66 cm ≈ 4 cm. Nüüd võiksime palli tagasipõrke kõrguse tõenäoseima (kõige sagedamini esineva) väärtuse h kui ühe kindla mõõdise kohta kirjutada h = (72 ± 4) cm. See tähendab, et igast sajast katsest põrkab pall 95 korral tagasi kõrgusele 68 kuni 76 cm. 

Kuid 4 cm pole enam korrektne mõõtemääramatuse hinnang keskväärtusele 72,46 cm. Tuleb ju arvestada, et keskväärtus on saadud saja mõõdise keskmistamisel, mistõttu valemi 2.6. kohaselt on standardmääramatus meie juhul

ja usaldatavust 95% omav mõõtemääramatuse hinnang vastavalt ligikaudu 0,4 cm. 

Mõõtetulemused, mis jäävad keskväärtusest kahe standardhälbega määratud vahemikku.	Mõõtetulemused, mis jäävad keskväärtusest kolme standardhälbega määratud vahemikku.

Seni oleme oma näites tegelenud ainult A-tüüpi hinnanguga mõõtemääramatusele. Kuna meie mõõtejoonlaua tootja pole skaalal esitanud infot mõõtejoonlaua täpsuse kohta, siis võtame B-tüüpi määramatuseks pool kasutatavast mõõtühikust (0,5 cm). Rangem statistiline käsitlus nõuaks küll veel selle täiendavat läbijagamist ruutjuurega kolmest (arvuga 1,73) ning seejärel kahekordistamist eesmärgiga viia usaldatavus 95% piirkonda. Kuna aga kaks viimast operatsiooni teineteist peaaegu tasakaalustavad (0,5 ^. 2 /1,73 ≈ 0,6) ning erinevust 0,5 cm ja 0,6 cm vahel me konkreetses katses nagunii ei tuvastaks, siis rahuldume B-tüüpi määramatuse hinnanguga 0,5 cm. Valemist 2.8 saame sel juhul usaldatavusega vähemasti 95% antud liitmääramatuseks

kusjuures ülespoole ümardamine on vajalik selleks, et tulemuse usaldatavus ei väheneks. Nüüd võime tagasipõrke kõrguse keskväärtuse kohta kirjutada

või realistlikumalt .