Füüsikas õppisin ma peagi välja nuuskima sügavusse viivaid radasid ja vältima kõike muud, kõiki neid arvutuid asju, mis ummistavad aru ja hälvitavad ta olulisest. Muidugi tõukas mind sellele protest sunduse vastu kuhjata eksamiks kõike seda kraami oma pähe, olgu siis meeleldi või vastutahtsi.
ALBERT EINSTEIN

Tavapäraselt väidavad tuntud teadlaste elulood, et nad olid väljapaistvad juba varajases lapsepõlves. Nagu paljud teisedki stereotüübid, ei sobi see üldsegi Albert Einsteini kohta. Olgugi ta XX sajandi kuulsaim teadlane, ainus, kelle pildi tunneb ära peaaegu iga haritud inimene maailmas, lapsepõlves iseloomustavad teda kõige paremini sõnad "tõsiselt alaarenenud".

Einstein sündis 1879 Lõuna-Saksamaal Ulmis üsna jõukas perekonnas. Üles kasvas ta Münchenis. Perekond oli seotud elektriasjandusega, mis tema noorusajal oli tehnika esirinnas. Üle kogu Euroopa mandri seati linnadesse elektrit. Tema elektriinsenerist onu ja tõeliseks bisnesmeniks ehk pisut liiga tagasihoidlik isa tegid ühiselt pingutusi, et leida kohake sellel paisuval turul.

Pisike Albert tegi vanematele peavalu vaevalise rääkimaõppimisega. Aga kui ta siis sellega ükskord hakkama sai, kõneles ta kohe täislausetes. Terane ja uudishimulik, ilmutas ta peagi muusikaannet. Onu märkas poisikese matemaatikataipu ja püüdis seda arendada. Varakult ilmnes tal võime ennastunustavalt mõtteisse süüvida.

Alberti õnnelik lapsepõli perekonna soojas ja leebes rüpes lõppes tema astumisega Müncheni Luitpoldi gümnaasiumisse. Seal olid juhtsõnadeks distsipliin ja autoriteet, kaks asja, mida Einstein jälestas kogu elu jooksul.

Kuigi ta jõudis enamikus ainetes hästi edasi, ajas Einsteini käitumine klassis õpetajad marru. Ta tavatses istuda tagapingis, unistavi silmi ja poolnaeratav, tegemata vähematki katset osutada õpetajatele oodatud austust ja teenistusvalmidust. Iseäranis riivatud oli direktor. Mänguplatsil hoidus nooruk kõrvale, põlates sportlikku rahmeldamist. Kergendustundega pöördus ta pärast tunde koju, armastatud viiuli ja "geomeetria pühakirja" juurde.

Enne Alberti viimase Õppeaasta algust kolisid vennaksed Einsteinid oma kiivakiskuva äri Paviasse Itaalias, jättes nooruki maha kooli lõpetama. Ilma jäetud hingelisest toetusest, ootas see värinal oma seitsmeteistkümnendat sünnipäeva: tollal oli see Saksamaal noormehele eriline tähtpäev. Sellest peale võis teda kutsuda väeteenistusse ja maalt lahkumise korral oleks ta tembeldatud väejooksikuks. Väeteenistuses oleks ta olnud perest hoopis ära lõigatud. Arvestades veel tema alalisi tülisid võimuritega, võis olla kindel, et koolivormi vahetamine välihalli vastu olnuks tõeline õnnetus.

Saanud arstist sõbralt vabastustõendi, lahkus Albert koolist ning Saksa kodakondsusest ja sõitis vanemate manu Itaaliasse. Kuid nende kolimine ei parandanud nimetamisväärselt majanduslikku seisu ega äriedu. Albert pidi vältimatult omandama mingi elukutse. Ta otsustas katsuda Õnne sisseastumiseksameil mainekasse Šveitsi Föderaalsesse Polütehnilisse Instituuti Zürichis. Seal võis ta jätkata õpinguid saksa keeles ilma Saksamaale naasmata. Eesmärk oli küllaltki tagasihoidlik: omandada keskkooli füüsika ja matemaatika õpetaja kutse.

Neis aineis olid ka eksamitulemused hiilgavad, kuid ta oli hirmus nõrk võõrkeeltes, keemias ja bioloogias. Polütehnikumi direktor andis nõu, et ta võiks eksameist mööda hiilida, kui ta saaks lõputunnistuse mõnest Šveitsi gümnaasiumist, kus eksaminõuded polnud nii kõrged. Ta juhatati Aarau kooli, mis oli tuntud oma sõbralikkuse poolest vaba vaimuga nooruse vastu. Kooli asutajaiks olid olnud haridusreformaatorid, kes eelistasid visuaalset kujutlusvõimet ja just see oli Alberti tugevaim külg. Hiljem on ta öelnud, et parimad ideed on talle ikka ilmunud kujutluspiltidena. Nende sõnadesse ja valemeisse panek on järgnenud kuid või koguni aastaid hiljem. Aarau osutus õnnelikult valitud siledaks teeks polütehnikumi.

Zürichis oli Einsteini edukus üpris ebaühtlane. Paljusid õppeaineid ei õpetatud tema meelest küllalt kaasaegselt. Seepärast puudus ta tihti loengutelt, et omal käel värskeimaid Õpikuid uurida. Oma sõbra Marcel Grossmanni hoolikaist konspektidest tuupis ta pähe vajaliku materjali kaheks kohustuslike eksamite rühmaks, vedades end niiviisi läbi. Lõpuks jõudis ta ka kooliõpetaja kutseeksamiteni. Õpingukaaslased pidasid teda sarmikaks ja teravmeelseks, mõned koguni lausa sädelevaks. Kuid lõpetamise ajaks oli tema vaevuvarjatud austusepuudus jõudnud ta vastuollu viia mõnede mõjukate professoritega. Lisaks ei olnud tal ikka veel Šveitsi kodakondsust. Väljavaated tööd leida polnud kaugeltki hiilgavad.

Kaks aastat ajas ta kuidagi läbi asendusõpetajana ja eratundidega, kuni Marcel Grossmann kasutas perekondlikke sidemeid, et hankida talle patendieksperdi tagasihoidlik koht Šveitsi pealinnas Bernis. Sel tavatult bürokraatlikul tööpostil sai ta nautida produktiivseimaid aastaid oma elus ja võib-olla kogu teadusloos. Seal leidis ta varju noorteadlast tavaliselt ahistava surve eest. Hilisemail aastail on ta märkinud:

Akadeemiline karjäär surub noore mehe ahistavasse kitsikusse, nõudes, et ta peab hulgiti tootma teaduspublikatsioone. See meelitab ta pealiskaudsusse, millele suudavad vastu seista ainult tugevad iseloomud. Seevastu on enamik praktilisi kutseid sellised, et normaalvõimetega inimene saab hõlpsasti nõutuga hakkama. Tema igapäevane eksistents ei sõltu mingitest erilistest inspiratsioonihetkedest. Kui tal on sügavamaid teaduslikke huve, võib ta sukelduda meelisprobleemidesse päevatöö kõrvalt. Teda ei ahista hirm, et tema pingutused ei pruugi kuhugi välja viia. Olen tänu võlgu Marcel Grossmannile, et võisin olla säärases õnnelikus olukorras.

Elu Bernis oli õdus. Ta sai hoopis paremat palka, kui võinuks teenida igatsetud koolmeistriametis. Peagi liitus ta väiksesse, kuid erksasse sõpraderingi, mis tavatses kohtuda napsutamiseks ja süvamõtete heietamiseks. Oma noorusuljuses kutsusid nad ringi Olümpiaakadeemiaks.

Selle idülli viljadeks oli relatiivsusteooria, küllap suurim ühe-mehe andam füüsikasse pärast Newtonit, ja olulised sammud kvantteooria poole. Tõhusalt aitas Einstein veenda ka viimaseid skeptikuid selles, et aatomid on tõepoolest olemas. PÕhiartiklid kogu selle temaatika kohta ilmusid palavikulisel llkuisel loomeõhinal 1905 ja 1906.

Einsteini kohta on muuhulgas käibel legend, et ta töötas aastaid tunnustuseta, enne kui maailm viimaks tema saavutusi hindama õppis. Tegelikult algas tema tähelend kohe pärast 1906. aastat. Selleks aitas tublisti kaasa Kesk-Euroopa kultuur, mis hindas kõrgelt just tema eriomadusi.

Tolleaegsed keskeurooplased olid näinud liiga palju sotsiaalset ja poliitilist segadikku, et veel uskuda varanduse, kuulsuse või poliitilise mõjuvõimu väärtusesse. Nad ei rajanud oma tulevikulootusi mitte kujunenud institutsioonidele, vaid mõistuse jõule. Nende silmis olid hea haridusega omandatud teadmised midagi, mida keegi ei saanud võõrandada. Lisaks kaldusid nad uskuma, et inimkonna progress johtus üksikute geeniuste tööst. Kui juba keegi sai otsaette potentsiaalse geeniuse märgi, olid talle kõik uksed valla ja tavakarjääri reeglistik lendas prügimäele.

Einsteinil vedas eriti sellepoolest, et mitte üksnes sõbrad, vaid ka mõned mõjukad teadlased, eriti Berliini ülikooli teoreetilise füüsika professor Max Planck, arvasid ta geeniuste kilda. Plancki arvamus kujunes üksnes Einsteini tollaseid artikleid lugedes, ammu enne nende kohtumist. Need tööd ilmutasid erakordset mõtteselgust, olgugi et autoril polnud veel mingeid ametlikke kraade ega positsiooni. Isegi Einsteini unelev, kuid ühtaegu läbitungiv pilk reetis tema geniaalsust. Nüüd juba kiirustas ta vormistama filosoofiadoktori väitekirja ja seadis sihid sootuks kõrgemale, kui oli senini söandanud.

1909. aasta tähistab Einsteini debüüti laias avalikkuses. Äsja saanud kolmekümneseks, sai ta esimese audoktori tiitli, kutsuti esinema oma ala juhtteadlastele kesksel teadusnõupidamisel, talle pakuti erakorralise professori kohta Zürichi ülikoolis. Hüpanud kähku üles akadeemilise trepistiku kahest astmest, kutsuti ta 1914 Berliini ülikooli erakorraliselt tema jaoks loodud kateedrit juhatama. Ta sai kõrget palka ja võis tegelda õppetööga vaid siis, kui ise soovis.

Einstein võttis neid austusavaldusi vastu segaste tunnetega. Ta oli õnnelik, et oli tõusnud oma kutse tippu. Päevast päeva sai ta nüüd suhelda oma ala parimatega, sest Saksamaa oli teadusuuringute esirinnas ja Berliini ülikool oli seal auväärseim. Kuid ühtlasi pelgas ta, et on nüüd "... hani, kellelt loodetakse ridamisi kuldmune". Ta otsustas jääda Šveitsi kodakondseks.

Teel Berliini peatus Einstein lapsepõlvekodus ja külastas oma kooli. Koolijuhataja kohtles teda reserveeritult, täis veendumust, et see kunagine lootusetu õpilane on nüüd puruvaene hädavares ja tuli tõenäoselt raha manguma.

Einsteini relatiivsusteooria põhipostulaat on petlikult lihtne:

Valguse kiirus on ühesugune kõikide vaatlejate jaoks, kõikvõimalikes suundades, hoolimata vaatleja või valgusallika liikumisest.

Eelmises peatükis käsitletud "eesõigustatud taustsüsteemi" valguses võib öelda, et Einsteini järgi olid kõik taustsüsteemid võrdselt privilegeeritud. Kuidas see saab nü olla?

Ilmselt tuleb arvestada Michelsoni-Morley katsetulemust kui kohustuslikku. Lihtsalt tuleb valida taustsüsteem, milles interferomeeter on paigal. Kuid paradoks on vältimatu: kui üks vaatleja tuvastab, et valguskiir liigub kiirusega c, kuidas saab siis teine vaatleja, kes liigub valgussignaali suunas, mõõta tema kiirust ja veel saada sama vastuse?

Kuigi Einstein tegi julge sammu, polnud ta ainus relativismist mõtleja. Umbes samal ajal jõudis Henri Poincare samalaadsetele järeldustele. Tema arvas, et Michelsoni nurjaläinud katse näitab, et on olemas üleüldine relatiivsusprintsiip, mis absoluutse liikumise tuvastamise keelab. Kuid Poincare oli juba vana, oma pikka väljapaistvat eluteed just lõpetamas, ja ta lootis probleemi lahendada eetri aluspõhjal. Oli vaja alles nõtke mõistusega nooremat meest, kes on küllalt tark tabamaks probleemi tuuma, kuid kes pole veel aheldatud tavalahenduste külge. Tarvis oli söakust võtta see printsiip arutluste lähteprintsiibiks, mitte aga tõestust vajavaks järelduseks.

Einstein taipas, et kuigi probleem näis olevat üksnes valguse liikumises, tõstatas ta hoopis sügavamaid küsimusi. Ta ei kohkunud ümber defineerimast näiliselt nii muutumatuid ja väljakujunenud mõisteid kui ruum ja aeg.

Einsteini arutlused pole matemaatiliselt rasked, kuid nende jälgimiseks tuleb end harjutada väga ebatavalise mõtlemisviisiga. Tuleb rangelt jälgida loogikat isegi siis, kui see näib argimõistusega vastuollu minevat. Enamik inimesi, isegi enamik teadlasi tavaliselt sedamoodi ei mõtle. Kuid viljakas mõtlemine liigub edasi kahel jalal, selles on ühendatud niihästi loogika kui ka intuitsioon. Leppige sellega, et te paratamatult, vähemalt esmatutvusel peate eelolevaid mõttekäike kummastavaks, niihästi järelduste veidruse kui ka mõtteviisi tavatuse tõttu.

Einstein ehitas relatiivsusteooria üles peaasjalikult mõtteliste katsete (sks. k. gedanken Experimented) varal. Kuigi põhimõtteliselt võimalikud, olnuks nood tegelikkuses sooritamatud. On tavaks saanud nende kaudu ka asja selgitada. Nii teeme siingi. Enne eesolevatesse loogikatihnikutesse murdmist on kasulik meelde jätta järgmised juhtnöörid:

1. Te võite alati eeldada, et just teie olete paigal ja valgus liigub kiirusel c teie suhtes.
2. Vaatlejal, keda teie peate liikuvaks, on täpselt samavõrd õigus pidada end paigalseisvaks ja sellele vastavalt kujundada oma kujutlus realiteedist.
3. Sellele vaatamata peavad kõik vaatlejad nii endi kui ka kõikide teiste vaatlejate tähelepanekuid pidama korrektseteks. Kui me relatiivsuspostulaadile toetudes võime kujutleda olukorda, milles saab vaidlustada vaatlustulemusi, siis on kas postulaat ise vale või siis ei saa sellist olukorda tegelikkuses ette tulla.
4. Vaidlused võivad käia üksnes nende seikade üle, mis vaatlustest järelduvad. Relatiivsusteooria õpetab meile, et teatavad omadused, mida me instinktiivselt omistame ümbritsevale maailmale, on tegelikult inimmõtte konstruktsioonid.

Kõik vaidlused kerkivad üht liiki järeldustest, nimelt eemal toimunud sündmuse toimumishetke hinnangutest, mida tehakse, arvutades, kui palju aega võtab sündmusest teavitamine valguse kiirusel.

Kaks Einsteini postulaadi otseseimat järeldust seisnevad selles, et (1) valguse kiirus on kõikvõimalike kiiruste ülempiir ja (2) kaks üksteise suhtes liikuvat vaatlejat ei pruugi jõuda üksmeelele selles, kas kaks sündmust toimusid ühtaegu või mitte. Esimene mõtteline katse, mida käsitleme, toob esile mõlemad punktid.

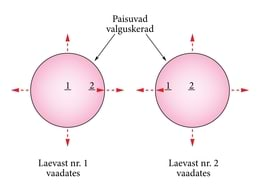
Kujutleme, et kaks kosmoselaeva mööduvad ilmaruumis üksteisest valguse kiirusele väga lähedase kiirusega. Sähvatagu nende lähenemisel laevade vahel ere välklamp (joon. 9-1). Eelmise punkti 1. juhtnööri järgi võib kummagi laeva meeskond uskuda, et ta on kiirusega c paisuva valguskera keskpunktis paigal. Teine laev on muidugi kusagil mujal. Kuid keral saab olla ainult üks keskpunkt. Juhtmõte 2 nõuab, et leiaksime, mil moel kummagi laeva mehed võiksid pidada end paigalpüsivaiks.

Laseme nüüd laevadel teha veel teise katse vastuolu lahendamiseks vaatluse teel. Peame nüüd eriti silmas 4. punkti, mis meile meenutab, et valguskera kui niisugune pole vaadeldav. Valgus levib küll igas suunas, kuid teda saab silmata üksnes ühes kohas ja ühel hetkel. Peame tõlkima väite "Ma olen kera keskel" millegi vaadeldava keelde. Siis võiks ta kõlada: "Välkest eemalduv valgus on minust igal hetkel ühekaugusel, olenemata suunast."

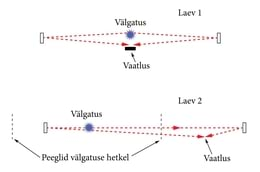
Lihtsaim viis seda väidet kontrollida on osa valgust tagasi peegeldada. Oletame, et suurel kaugusel ühest laevast on paigaldatud kaks peeglit, liikumissuuna suhtes ette ja taha. Kui välked jõuavad mõlemalt peeglilt laeva tagasi samaaegselt, peab ta olema kera keskpunktis. Sealsed vaatlejad võivad tõestuseks kiirkatikuga kaamera abil teha isegi foto, mis näitab kummagi peegelduse üheaegsust. Paraku ei lahenda see väitlust põhjusel, mida näitab joonis 9-2.

Teise laeva meestel on samuti juhtunu seletus valmis. Kuna nemad näevad laeva ja reflektoreid üksteise suhtes kärmelt liikumas, siis tagapoolne peegel tormas valgussähvatusele vastu, eespoolne aga eest ära. Selge see, et valgus põrkub kõigepealt tagumisele peeglile, alles pisut hiljem eesmisele. Peegeldumisel pöördus kumbki valguskiir tagasisuunas. Tagumine kiir peab nüüd tormama eemalduvale kosmosesõidukile järele, eesmisele kiirele kihutab laev ise vastu. Nagu skeemilt näha, kummagi kiire teekond koosneb lühikesest ja pikast harust. Tahapoole suunduv valguskiir läbib esmalt lühikese ja siis pika haru, eenduv kiir needsamad vastupidises järjekorras. Kuid mõlemal juhul on harude pikkused võrdsed, kogusummas kulub mõlemal kiirel ühepalju aega, olenemata lühikese ja pika haru järjekorrast.

Seega väidab see meeskond, et välked mõlemalt peeglilt jõuavad laeva samal hetkel. Kuid nad eitavad, et kiired põrkusid peeglitele samal ajal. Nad ei vaidlusta vaatlustulemusi, kuid eitavad, et need näitavad, nagu teine laev oleks olnud valguskera keskpunktis. Vaidlus taandub küsimusele, kas valgus jõudis mõlema peeglini samaaegselt. Seda aga ei saa lahendada vaatluse teel. Kumbki meeskond võib häirimatult jääda oma väidete juurde. Mitte keegi ei saa otseselt kogeda, mis juhtub kahes eri kohas, seepärast jääb vaidlus lahenduseta. Õigus on mõlemal. Relatiivsuspostulaat on esimesele proovile vastu pidanud. Kuid selle eest tuleb maksta. Peame loobuma mõttest, et väljendil "juhtus samal ajal" on ühene tähendus kõikide vaatlejate jaoks, kui kaks sündmust leiavad aset eri kohtades. See näiliselt süütu ajamäärang on nüüd kõrvaldatud faktide hulgast ja taandatud kokkuleppeks.

Kujutleme, et kahe kosmoselaeva suhteline kiirus eelmises näites oli suurem kui c. Sel juhul võib kumbki meeskond väita, et teine laev oli väljaspool paisuvat sfääri. Nad isegi ei pruukinud välgatust näha! Kuid arutlusreeglid 1 ja 2 nõuavad, et mõlemad meeskonnad peavad igal juhul välgatust nägema. Kuna 3. punkt ei luba lahkhelisid tegelike vaatluste suhtes, peavad c-st suuremad kiirused olema välistatud.

Eelmises peatükis kogesime, et γ arvutamiseks peab v olema c-st väiksem. Nüüd näeme selle võrratuse relativistlikku sisu. Tõsi, 3. juhtnöör lubab meil ka loobuda relatiivsuse postulaadist. Kuid kuna valguse kiirusest suuremaid kiirusi pole kunagi täheldatud, pole meil mingit põhjust seda teha.

Teisiti öeldes, kui miski liigub kõikides taustsüsteemides võrdse kiirusega, siis see on ainus säärane kiirus ja ta on kõikvõimalike kiiruste piirväärtus. Ei saa olla kaht erinevat kiirust, mis mõlemad alluksid Einsteini postulaadile. Oleme jõudnud väga olulise seigani: relatiivsuspostulaat ei käi mitte valguse enda, vaid nimelt valguse kiiruse kohta.

Nüüd hakkame valguse kiirusse hoopis teisiti suhtuma. Ta ei ole enam valguse juhuslik omadus ega ka valguse levikeskkonna omadus. Meie arutluskäik ei puudutanud ju üldse valguse loomust ega mingit keskkonda. Ainus asi, mida me eeldasime, on see, et valgus levib kõigis taustsüsteemides ühesuguse kiirusega. Oleme jõudnud millegi väga üldiseni. Järgmises peatükis veendume, et valguse kiirus pole pelgalt elektromagnetlainete omadus, vaid et ta on universumis fundamentaalne mastaabitegur ruumi ja aja vahel.

Siinkohal ei saa me veel öelda, mis on selle kiiruspiirangu peale pannud. Miks näiteks ei või rakett valguse kürusest edasi kiireneda? 11. peatükis, kui jõuame Newtoni seaduste muutusteni, mida nõuab relatiivsusteooria, leiame, et kiiruspiirang tingib enda ise.

Nüüd jõuame teise mõttelise katseni, mis oli Einsteini enda lemmikuks. Tegemist on liikuva objekti pikkuse mõõtmisega. Küllap talle turgatas see pähe, kui ta sõitis tööle patendiametisse mööda Berni kitsaid tänavaid. Muidugi asendus kolisev trammivagun tema vaimusilmas uhke ekspressiga, mille kiirus valguse omast ainult õige pisut maha jääb.

Siin tuleb silmas pidada, et liikuva objekti all mõistame siin objekti, mis liigub mõõdupuu suhtes, millega tema pikkust mõõdetakse. Kui mõõdupuu liiguks objektiga kaasa, mõõdaksime tema pikkust taustsüsteemis, milles objekt on paigal.

Kujutleme, et raudtee ääres on postidel telefoniliin, postid on püstitatud võrdsete vahemikega ja igal postil on hästinähtav number. See ongi meie mõõdupuu. Et rongi pikkust mõõta, tuleb lihtsalt tähele panna, milline post on samal hetkel kohakuti rongi esiotsaga ja milline tagaotsaga. Esimesest mõttelisest katsest juba teame, et nõue samal hetkel pole hoopiski lihtlabane.

Üht mõõtmisproovi illustreerib joonis 9-3. Paigutame rongi keskele välklambi, mis on nähtav mõlemasse otsa. Nähes sähvatust, panevad rongi kummaski otsas olevad vagunisaatjad tähele lähima posti numbri. Paraku röögatab maas seisev raudteevaht otsemaid: "Vale!" Mõõtmine on kehtetu, sest postide numbreid ei vaadatud samal hetkel.

Tema näeb asja nii, nagu kujutatud joonise alumisel poolel. Rongi lõpus olev saatja liikus välke poole ja nägi seda varem kui paariline rongi peas, kes liikus eemale ja tegi oma vaatluse hiljem. Vahepeal on rong liikunud ja reeperpostid on teineteisest kaugemal kui rongi pikkus. Raudteevaht peab rongi lühemaks kui saatjate täheldatud postide vahekaugus.

Loogiline on lahendada dilemmat, väites, et liikuvad objektid peavad liikumissuunas kokku tõmbuma. Siis võivad nii vaatlejad rongis kui ka maapinnal kokku leppida, et maaga seotud liikumatus taustsüsteemis on vahemik postide vahel suurem kui rongi pikkus.

Liikuvad vaatlejad leiavad, et põhjus on "mõõdupuu" lühenemises: postid on üksteisele lähenenud, nende vahemikke mahub rongi pikkusele rohkem. Raudtee kõrval seisev vaatleja jällegi selgitab, et vahemaa postide vahel on suurem kui seisva rongi pikkus, sest pole õige mõõta paljalt rongi. Tegemist on kahe vahemiku summaga: rongi pikkus pluss teepikkus, mille ta edasi liikus rongi peast ja sabast tehtud vaatluste vahel. Seega on rong lühem kui paigalseisus, kuid postide vahemik on ikkagi suurem kui seisva rongi pikkus.

Vaatluste õigsust ei vaidlustata. Raudteevaht soostub uskuma, et kumbki rongisaatja tabas lähima posti numbri õigesti sähvatuse nägemise hetkel. Ta ei ole nõus ainult sellega, et mõlemad tegid seda ühel ja samal hetkel. Kuid see on vaid järeldus: ei ole võimalik võrrelda ajahetki kahes eri kohas otsese vaatluse teel. Asi pole mitte ühegi asjaosalise meelte täpsuses ega mõõteriistade lugemites. Ei, see on osa sellest tegelikkuse pildist, mille me kujundame oma arus. Einstein andis piirile välise ja meie peas toimuva vahel uue määratluse. Loodus ei määratle taustsüsteeme, seda teeme vaid meie.

Kuigi taustsüsteemi valik on meelevaldne, on see Einsteini järgi ikkagi kehtiv ja kasulik, kui vaid arvestatakse valiku eriseiku. Kaks raudteevahti võivad ohutult ületada rööpmed üksteisest kaugusel, mis on väiksem seisva rongi pikkusest, tehes seda hetkel, mida nemad peavad samaaegseks.

Selliselt analüüsis Einstein Lorentzi kokkutõmmet. Järgnevas peatükis näeme, et ta jõudis ka kvantitatiivselt samale tulemusele kui Lorentz. Vahe on selles, et kui Lorentz nägi kontraktsioonis mehaanilist efekti, mis johtus liikumisest eetri suhtes, siis Einsteini käsituses oli see taustsüsteemi valiku tagajärg. Raudteevahi meelest on rong lühenenud, sõitjate arvates mitte. Lorentzi jaoks on v tema valemis kiirus eetri suhtes. Einsteinil on see objekti kiirus mingis suvaliselt valitud taustsüsteemis. Miks siis mitte teha asja endale lihtsamaks, valides süsteemi, milles v = 0?

Vaatame ses valguses uuesti üle Michelsoni-Morley katse. Kui taustsüsteemiks on Maa, siis kokku tõmme puudub, sest valgus liigub ühesuguse kiirusega interferomeetri mõlemas harus. Süsteemis, milles Maa liigub, tähendab kokkutõmme, et mõlemad kiired läbivad sama teepikkuse, nagu seda kirjeldas Lorentz. Mõlemad taustsüsteemid annavad sama vaatlustulemuse. Eelissüsteeme ei ole ja eetrit ei saa enam uskuda.

Argimõistusega läheb see vastuollu üksnes seetõttu, et me eeldame intuitiivselt, et see, mida me praegu näeme, ka praegu juhtub. Tavakogemusest lähtudes on see igati mõistlik. Mitte väga kauged objektid ei liigu ju märgatavalt nende mikrosekundite või veelgi lühemate ajavahemike jooksul, mil valgus jõuab nendelt meieni. Seevastu väga kiiresti liikuvate objektide puhul muutuvad need väikesed viivised oluliseks.

Võime kasutada Einsteini rongi, osutamaks veel ühele relativistlikule efektile. Kujutleme, et vagunisaatjad tahavad vältida valgussignaalidega kaasnevaid probleeme ja kohtuvad rongi keskel, kus nad seavad oma kellad ühte. Siis lähevad nad oma vaatluspunkti rongi peas ja sabas ning märgivad postinumbrid eelnevalt kokku lepitud hetkel. Kui maailm on endaga kooskõlas, peab tulemus olema sama kui äsja kirjeldatud meetodil. Raudtee ääres seisja peab ikka eitama, et poste fikseeriti samaaegselt. Järelikult peab kelladega midagi juhtuma ajavahemikul, mis möödus nende ühteseadmisest kuni vaatluste tegemiseni. Järgmises peatükis saame teada, mis nimelt.

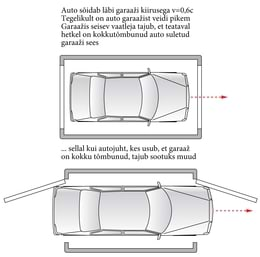
Lõpetame peatüki kolmanda mõttekatsega. Kujutleme garaaži, mille mõlemas otsas on uksed, mis avanevad automaatselt, kui auto läheneb, ja sulguvad, kui auto on uste vahelt möödunud. Olgu seisev auto garaažiga ühepikkune. Kihutagu auto läbi garaaži valguselähedasel kiirusel. Siis peab ta garaažis seisja meelest olema lühenenud. Tagumine uks avaneb, et autot läbi lasta ja siis sulgub tema taga, enne kui eesuks jõuab tema väljalaskmiseks lahti minna. Hetkeks on auto suletud graažis.

Kuid uljalt kihutava autojuhi arvates on garaaž lühenenud. Tema näeb asja nii, et mingil hetkel peab auto mõlemast otsast välja ulatuma ja mõlemad uksed korraga lahti olema. Joonisel 9-4 on toodud mõlemad konfliktsed pildid. Tavamõistuse järgi peab üks või teine olema vale.

Relatiivsusteooria järgi aga ei ole küsimusel ühest vastust. Vigur seisneb uste avanemise ja sulgumise järjekorras, nii nagu seda näevad eri vaatlejad. Võtame selle kokku:

Paneme tähele teise ja kolmanda sündmuse järjekorra vahetust. Garaaži kinni- ja lahtiolek on järjekordne näide eri kohtades aset leidvate sündmuste toimumisaja võrdlemisest. Tulevas peatükis analüüsime, mida juht ja seisja garaažis tegelikult näevad, siis ehk saame asjast täielikuma pildi.

Tuleb rõhutada, et relatiivsusteooria EI eita, et olemas on üksainus tegelikkus ega võta omaks erinevate vaatlejate vastakaid isiklikke realiteete. Einstein oli veendunud, et teadus kirjeldab asju, mis eksisteerivad olenemata mistahes vaatlejaist. Selles näites on niihästi auto kui ka garaaž reaalsed, samuti kui uste avanemised ja sulgumised ning kõik muu, mida juht ja teised näevad. Teatud mõttes ei ole reaalsed vaid meie joonistatud pildid joonisel 9-4. Nad on tegelikkuse kujutamise leppelised viisid. Järgnevast loeme, et need pildid ei esita hoopiski seda, mida kumbki vaatleja tegelikult näeb.

Kõige paremini kirjeldab sääraste piltide saamislugu sõna konstrueerima. Pildid ei esita vahetut kogemust. Nad on konstrueeritud vaatluste järgi, võttes arvesse ajavahemikku, mis kulub valgusel vaatlejani jõudmiseks. Nagu kord ja kohus saame neid konstruktsioone koostada üksnes eespool esitatava kvantitatiivse aparaadi varal.

Selles protseduuris ei ole midagi uut ega isegi eriti "teaduslikku". Kunstnik kujutab kolmemõõtmelist tegelikkust kahemõõtmelisel lõuendil, rakendades teatavat konventsiooni, nimelt perspektiivi. Insenerid eelistavad oma tehnilistes joonestustes garaazi taustsüsteemis auto taustsüsteemis esitada kolme vaadet. Loodus ei dikteeri meile, kumba eelistada. Kumbki ei hõlma objekti kogu tema olemuses, nii kui bilansiaruanne ei suuda esitada ärist kõike.

Kui äriraamatud ei peegelda äriseisu õigesti ja ülevaatlikult, võib valida uue raamatupidamissüsteemi. See on ka füüsikas nii. Seal nimetatakse “täiuslikumat raamatupidamist" neljamõõtmeliseks aegruumiks.

Albert Einsteini loomus, kasvatus ja haridus valmistasid teda uutmoodi mõtlema, kuid miski ei ennustanud tema hiilgavat edukäiku 1905. aastani, mil ta kirjutas viis erakordse väärtusega artiklit. Kahes neist esitas ta relatiivsusteooria. Selle lähtepunktiks on postulaat, et valgus levib kõikides taustsüsteemides ja kõikides suundades ühe ja sama kiirusega. Et see oleks võimalik, teisendas ta aja ja ruumi mõisteid. Seejuures seadis ta tingimuseks kooskõla vaatlustega. Rea mõtteliste katsete varal näitasime, et see postulaat välistab valguse kiirusest suurema kiirusega liikumise ja viib vastakatele arvamistele selle kohta, kas kaks sündmust eri paikades toimuvad samal ajal või mitte. Siit omakorda lähtuvad vastuolud liikuva objekti pikkuse määrangutes.

Alice naeris: "Pole mõtet proovida, võimatuid asju ei saa uskuda."
"Julgen arvata, et sa pole seda küllalt harjutanud," sõnas Kuninganna. "Kui ma olin sinuvanune, pühendasin sellele iga päev pool tundi. Või veel, mõnikord uskusin ma juba enne hommikueinet koguni kuut võimatut asja."
LEWIS CARROLL, Läbi peegli

Lahkheli saab lahendada kahte moodi. Esiteks võib lihtsalt harjutada end sellega leppima, kuni kõik osapooled mõistavad ja respekteerivad üksteise vaatekohti. Teine viis on leida ühine alus, millega osapooled võivad soostuda. Relatiivsusteooria pakub mõlemaid võimalusi lahendada vaatlejate vahel dispuute, mis järelduvad Einsteini postulaadist.

Lepitava lähenemise andis Einstein esimeses artiklis, mille ta saatis ajakirjale Annalen der Physik juunis 1905. Seal on esitatud viis, kuidas iga vaatleja saab oma tegelikkusepildi mistahes taustsüsteemis tõlkida millisesse tahes teise taustsüsteemi. Selles peatükis näitame kõigepealt, kuidas see tõlkimine käib.[*[Relatiivsusteooria standardterminoloogias nimetatakse vastavaid teisendusvalemeid Lorentzi transformatsioonideks e. teisendusteks.]*] Ühtlasi näeme, et looduse tavakirjeldus on tinglikum ja kunstlikum, kui oskame arvatagi. See osa valmistab teed ühisaluse, neljamõõtmelise aegruumi esitluseks.

Eelmises peatükis selgus, et alati, kui kasutame ühes taustsüsteemis saadud teavet selleks, et luua asjast pilti teises süsteemis, peame omaks võtma kolm sätet, mis on tunduvas vastuolus meie tavakujutlustega ajast ja ruumist:

1. Liikuvad kellad näivad aeglasemalt käivat.
2. Liikuvad objektid näivad oma liikumissihis lühenevat.
3. Sündmused, mis on samaaegsed ühes taustsüsteemis, ei pruugi seda olla teises süsteemis.

Et segadust leevendada, käsitleme neid efekte ühekaupa, ülaltoodud järjekorras.

Relatiivsuspostulaat nõuab, et valguse kiiruse mõõtmine peab alati andma sama tulemuse, vaatamata sellele, millises taustsüsteemis ta on sooritatud või mis suunas valgus levib. Et mõista, mis sellest postulaadist järeldub aja mõõtmise kohta, vaatame aja mõõtmist liikuvas rongis.

Tulemus peab näitama, et valgus liigub ettearvatud kiirusel rongi suhtes. Ühtaegu peab rongi kõrval seisev vaatleja saama kasutada sedasama mõõtmistulemust näitamaks, et valgus levib täpselt samal kiirusel ka Maa suhtes.

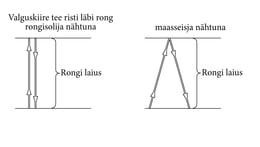
Teeme mõõtmise ainsa kellaga [*[Õieti stopperiga, mida relatiivsusteooria mõttelistes katsetes nimetatakse lihtsalt kellaks. (Tõlk.)]*], mis asub rongis, võttes rongi sõidusuunaga risti leviva valguse edasi-tagasi teekonna aega. Ühe kella kasutamine kõrvaldab eri kohas olevate kellade sünkroniseerimise raskuse. Edasi, ristsuunas leviva valguse puhul pole muret rongi laiusega, sest selles suunas puudub liikumiskomponent Maa suhtes.

Maas seisev vaatleja peab nõustuma kõigi rongis tehtud mõõtmiste õigsusega, kuid ta võib neid tõlgendada mistahes viisil, näitamaks, et valgus levib nii rongi kui ka Maa suhtes ühesuguse kiirusega.

Jooniselt 10-1 on näha, et kummagi vaatleja arvamused lähevad lahku valguse poolt läbitud teepikkuse suhtes. Kui sõitjale tundub, et kiir jõuab lähtepunkti tagasi, siis kõrvalseisja meelest jõuab ta hoopis edasi nihkunud punkti. Seepärast ei tehtudki mõõtmist Maa taustsüsteemis: siis oleks läinud vaja kahte kella. Geomeetriliselt on olukord täpipealt sama kui ujujaga (ptk. 8). Kui rongi laius on $w$, siis kaasasõitva vaatleja meelest läbib kiir vahemiku $2w$, maas seisva vaataja arvates aga vahemiku $2\gamma w$.

Laseme nüüd kummalgi vaatlejal arvutada valguse kiiruse. Vastavalt relatiivsuspostulaadile peavad mõlemad saama vastuseks $c$, mis on 300000 km/s. Sõitja jagab läbitud vahemikuajaga $t$, mida tema stopper-kell näitab:

Seisja rehkenduses peab lugejas olema $2\gamma w$. Kuidas siis saada vastuseks seesama $c$? Kuna vaatlejatel pole lahkarvamusi rongi laiuse $w$ suhtes, siis katsumegi sellest lähtuda. Õige vastuse saamiseks on vaid üks tee: korrutame ka lugejat $\gamma$-ga. Siis gammad taanduvad ja vastus tulebki sama,

Mis on $\gamma t$ tähendus nimetajas? Kuna lugejas on valguse teepikkus Maa taustsüsteemis, siis peab nimetajas seisma aeg, mis möödus sama taustsüsteemi kella järgi. Ainult siis annab jagatis valguse kiiruse Maa süsteemis. Kuna $\gamma$-ga korrutamine suurendab $t$-d, on seisvas taustsüsteemis kulunud rohkem aega, kui liikuv kell näitab. Seda tähendabki väide, et liikuv kell käib aeglasemalt, s.o. jääb maha.

Kuid sõitja suhtes liiguvad kõik maas olevad kellad, siis peavad just need maha jääma. Kummagi vaatleja meelest kasutab teine mahajäävat kella.

Kui te tõrgute omaks võtmast väidet, et kaks vaatlejat üheaegselt peavad teise kella mahajäävaks, siis pidage silmas seda olulist tõika, et üksteise suhtes lükuvail vaatlejail on ainult üks võimalus oma kelli vastakuti võrrelda, nimelt möödumishetkel. Seejärel kaugenevad nad kiiresti teineteisest. Siis võivad nad teateid vahetada üksnes valguse või raadiosignaalide kaudu. Nende levik aga võtab aega, seda enam, mida kaugemale nad üksteisest jõuavad. Kumbki arvutab teise kella lugemi, tehes paranduse sellele viivisele, eeldades, et nimelt teine liigub. Nende paranduste vahe aiva kasvab. Edaspidi toome selle kohta ka arvulise näite.

Tulles tagasi eelmise peatüki ronginäite juurde, laseme sõitjail kohtuda keset rongi ja seada seal oma kellad ühte. Seisev raudteevaht väidaks, et rongis vastassuunas liikudes muudavad sõitjad oma kiirust Maa suhtes. Rongi peasse suunduja liigub kiiremini, seepärast peab tema kella käik olema aeglasem kui rongis paigal oleval kellal. Rongi sappa mineja kellal aga peab olema kiirem käik, sest tema liigub aeglasemalt. Jõudes rongi otstesse, pole nende kellad enam sünkroonis. Jällegi tuleb välja, et rongi sabaga rinnastuvat posti täheldatakse varem kui rongi peaga kohakuti jõudvat.

Nüüd on meil olemas liikuva kella aeglustumise kvantitatiivne mõõt. Seda saame kasutada, et arvutada liikuva objekti näivat kokkutõmbumist liikumissuunas. Veeretame taas välja Einsteini rongi. Tema pikkust saame hõlpsasti mõõta, tehes kindlaks rongi kiiruse ja siis mõõtes stopperiga tema möödumisaja.

Rongis sõitja võib selle mõõtmise vaidlustada: "Mõõtmine on tehtud mahajääva kellaga, seepärast on pikkus lühem kui peaks." Samuti kui valguse kiiruse mõõtmiselgi, korrutab ta stopperi ajanäidu γ-ga, et saada temale usutavat tulemust. Kuna ta rongi pikkuse leidmiseks korrutab aja kiirusega, saab ta γ korda suurema pikkuse kui maas seisev vaatleja.

Kui relativism on endaga kooskõlas, peab see parandatud mõõtarv ühilduma rongi suhtes paigal seisva mõõdupuuga hinnatuga. Niisiis, kui rongis sõitev vaatleja teeb sellise mõõtmise ja teatab tulemuse seisjale, peab too jagama γ-ga, et saada liikvel rongi pikkust. Muidugi on see veider viis rongi mõõtmiseks, aga kui relatiivsusteooria on õige, on ta sama hea kui iga teine ja peab andma ka sama tulemuse.

Kokkuvõttes saame üleminekureeglid ühes taustsüsteemis tehtud mõõtmiste teisendamiseks teise süsteemi:

• Kui sinu suhtes liikuv vaatleja teatab mingi ajavahemiku, siis korruta seda γ-ga, et saada ajavahemikku omas süsteemis.
• Kui sinu suhtes liikuv vaatleja teatab mingi pikkuse piki liikumissuunda, siis jaga seda γ-ga, et saada pikkust omas süsteemis.

Kui lugeja eelistab valemeid (kui mitte, võib järgneva lõigu ja valemid vahele jätta), siis tähistame liikuva objekti pikkuse liikumissuunda mööda tähega L, objekti laiuse (risti liikumissuunaga) tähega W ja ajavahemiku t-ga. Märkigu alaindeks null suurust, mis on mõõdetud paigalolevas taustsüsteemis (L₀ ja W₀ on mõõdetud objekti suhtes liikumatute mõõdupuudega, t₀ – liikumatu kellaga). Siis taustsüsteemis, milles objekt või kell liiguvad, saame:

Kui olete nüüd läbinisti pahviks löödud (üleüldine tunne relatiivsusteooriaga tutvumisel) liikuvate objektide ahenemisest ja kelladest, mis lasevad ajal kaotsi minna, võiks mõnede arvude meenutamine mõjuda rahustavalt. Kiireimad suuremõõtmelised inimtooted, mandritevahelised raketid, liiguvad kiirustega umbes üks kümnetuhandik valguse kiirusest. Siis γ erineb ühest vaid sajamiljondiku võrra. Ülehelikiiruslike lennukite puhul kahaneb see arv ühe sajamiljardikuni.

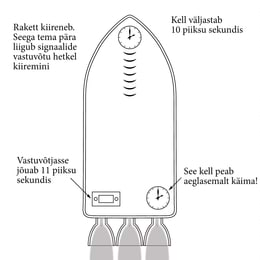
Esitame nüüd dialoogi kahe astronaudi vahel, mis näitab, kuidas kaks üksteise suhtes liikuvat isikut võivad mõlemad korraga arvata, et nimelt teise kell jääb maha. Rõhutagem, et kellade võrdlemine nõuab teabevahetust üle suurte ja ühtlasi muutuvate vahemaade. Seejuures peavad nad arvestama ajalisi viiviseid infovahetusel üle määratute distantside. Tahame näidata, et kui nad ei arvesta relativistlikke parandusi, ei jõua nad kokkuleppele selles, mida kummagi kellad peaksid näitama. Õigesti parandusi tehes on nad kellade lugemitega nõus, aga jäävad eriarvamusele toimuva üksikasjus.

Kaks astronauti, Jüri ja Juta, mööduvad ilmaruumis üksteisest suurel kaugusel suhtelise kiirusega 0,6c. Hetkel, mil nad läkitavad üksteisele välgatuse, ajavad nad kellad ühte ja Juta lubab saata kümme minutit hiljem raadioteate (mis lngub valguskiirul). Järgneb selline dialoog:

JUTA: Kui kõlab piiks, on kümme minutit möödunud.

JÜRI: Ahhaa! Täpselt nagu Einstein ütles, sul on kell taga! Kui sa tõesti oleksid 10 minuti pärast ühendust võtnud, oleksid pidanud olema 6 valgusminutit eemal ja ma oleksin saanud teate 10 + 6 = 16 minuti pärast. Paraku pean ütlema, et minu kell näitas sinu piiksul 20 minutit. Relatiivsusteooriast tuleb sinu liikumiskiirusel gamma 1,25. Tegelikult astusid sa kontakti 12,5 minuti pärast, kui olid 7,5 valgusminuti kaugusel. See annab kokku 20, nagu ma ütlesin.

JUTA: Okei, puupea, loe oma Einstein uuesti üle! Tema lubab seda mängu kahekesi mängida, ja ma võin samahästi põhjendada, et hoopis sinu kell on taga. Minu arvates liigud sina ja olid ainult 6 valgusminuti kaugusel kui ma läksin saatele. Kuid sa pagesid mu sõnumi eest, mis pidi su kinni püüdma suhtelisel kiirusel 0,4c. Läks 15 minutit, et teha tasa su 6 valgusminutit, nii et tegelikult said signaali 25 minuti pärast. Sina ütled aga, et 20 minuti pärast, nii et maha jääb sinu kell.

JÜRI: Minu meelest tead sa ainult seda, mida sinu kell näitas saatehetkel, ja mina tean, mida näitas minu oma, kui ma signaali vastu võtsin. Meie aga vaidleme selle üle, mida minu kell näitas saatehetkel või sinu oma vastuvõtuhetki. Sel pole ju midagi tegemist tegelike vaatlustega, sest me oleme üksteisest miljonite kilomeetrite kaugusel!

JUTA: Tõsi jah! Kas pole nadi, et me ei saa nõustuda nende arvestustega, selleks et nõustuda kellade tegelike näitudega!

Ilma relativistlike parandusteta pidanuks Jüri arvates tema kell Jutalt sõnumi saamise hetkel näitama 16 minutit, Juta arvates aga 25. Teinud parandused, nõustuvad mõlemad, et ta näitab 20.

Tuleb rõhutada, et kummalgi on täielik vabadus võtta omaks teise vaatepunkt, või ka eeldada, et mõlemad kosmoselaevad on liikvel (ainult siis tuleb arvutus palju tülikam). Tera on selles, et relatiivsusteooria järgi pole mingit vahet millist taustsüsteemi te kasutate – kõik on võrdväärsed kahe vaadeldava sündmuse tõlgendamiseks.

Mis aga juhtub siis, kui üks astronautidest pöördub tagasi kellade otseseks kõrvutamiseks? Selgub, et on oluline vahe, kumb just tagasipöörde teeb. See on kuulus kaksikute paradoks, millest kuuleme veel edaspidi lähemalt. Suhe 2:1 saatja ja vastuvõtja kellade näitude vahel jääb kehtima ka kõigi järgnevate sideseansside jaoks. Jüri vastus, saadetud, kui tema kell on 20 minuti peal, jõuab kohale, kui Juta kell näitab 40 minutit, ja tema vastus jõuab Jürini 80 minuti näidu hetkel. Kui v = 0,8c, on suhe 3:1.

Kummagi astronaudi täheldused ja arutlused on kokku võetud tabelis 10-1. Arvutuste lihtsustamiseks on kaugused antud valgusminutites, s.o. vahemikes, mida valgus läbib ühe minutiga (18000000 km). Kui nüüd mõõta kiirusi valgusminutites minuti kohta, tuleb valguse kiiruseks 1,0 ja kosmoselaevade suhteline kiirus on siis 0,6. Peame silmas, et kõikidest tabelis toodud arvudest esitavad ainuüksi kaks rasvaselt trükitut tegelikke vaatlusandmeid. Kõik ülejäänu kuulub pealisehitisse, mille püstitame, et saada seletatavat pilti tõelusest.

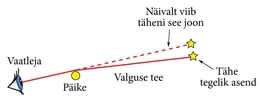
Oleks aeg seletada, mida me mõistsime "tegelikkuse piltide" all 2. juhtnööris. Kui tegemist on kiiresti liikuvate objektidega, siis ei ole need pildid sugugi see, mis on silmnähtav. Silmnähtavalt on asjade eri osad eri kaugustel ja seetõttu näha eri aegadel. Järgnevas mõttekatses näeme, kuidas kaks vaatlejat, teataval hetkel ühes ja samas kohas asudes näevad oluliselt sama kujutist, kuid kasutavad seda vasturääkivate piltide konstrueerimiseks.

Liikugu auto garaaži suhtes (9. ptk.) suhtkiirusega 0,6c ja olgu kumbki 20 jalga pikk. Inglise jalgade kasutamist ses näites õigustab lihtne seos: valguse kiirus on umbkaudu 1 jalg nanosekundis (ns, miljardik sekundit). Olgu meie vana sõbratar Juta roolis, kusjuures ta asub just auto keskkohas. Garaaži keskel seisab Jüri.

Hetkel, mil Juta möödub Jürist, on nad silmapilguks peaaegu samas kohas ja peaksid nägema ligilähedalt üht ja sama. Kui mõlemad vaatavad sõidusuunas, siis nad näevad, et auto esiots on garaažis poolel teel ukseni.[*[Seda saab tõestada, tehes läbi tabelis 10-2 toodud arvutused, ainult tagurpidi.]*]

Kumbki mõistab, et selles pole midagi uut: valgusel kulus aega nendeni jõudmiseks. Selle aja sees jätkas auto liikumist ja et tabada, kus miski on praegu, peab tegema parandusi, arvestamaks liikumist.

Jüri muretseb auto esiotsa pärast: kas on too jõudnud uksele küllalt lähedale, et automaatuks avaneks. Juta taustsüsteemis liigub uks ja teda huvitab, kas uks on juba jõudnud esipõrkerauani. Konks on selles, et parandusi teeb kumbki erinevalt, sest neil on eri mõõdupuud.

Kumbki peab oma süllapuud paigalseisvaks. Jüri hindab kaugusi ukse järgi, mida ta teab olevat 10 jala kaugusel. Järelikult peab auto esiots olema 5 jala kaugusel. Juta taustaks on auto, ja kuna esiots on temast 10 jala kaugusel, peab tema arust ukseni olema 20 jalga. Tabelis 10-2 on kokku võetud, kuidas kumbki korrigeerib nähtavat pilti, arvestades valguse leviaja jooksul toimuvat liikumist.

Kuna uks on kaugeim punkt garaažis ja auto esiraud auto kaugeim punkt, siis arvab Jüri, et auto on kokku tõmbunud, kuid Juta on sama kindel, et ahenenud on hoopis garaaž. Vahe tuleb sellest, et Jüri teeb paranduse auto esiotsa liikumise järgi. See paistab talle 5 jala kaugusel. Juta parandab ukse liikumise järgi ja seda näeb ta 20 jala kaugusel. Tema ajaparandus on siis Jüri omast 4 korda suurem, ja selle jooksul saab toimuda neljakordselt pikem suhtliikumine.

Siin peitub relatiivsusteooria tuum: kaugeid objekte ei näe me iial sellistena, kui nad on praegu, vaid nii, nagu nad olid mõni aeg tagasi. Kui nad on liikvel, tuleb sisse viia parandused sellele liikumisele, kuid selleks pole mingit ühest õiget vüsi. Lõigata "viilakuid ajas", eraldada suuri ruumiosasid samal ajahetkel, on vaid pettekujutlus, inimaru konstruktsioon, mis ei vasta meie tegelikule tajule.

Tõsi küll, argielus ei liigu esemed nii kiiresti kui mõttelistes katsetes ja nanosekundid on naeruväärselt lühikesed ajavahemikud. Seepärast töötab see kujutlus hästi ja intuitiivselt mõtleme ikka sedaviisi. Selline käsitus hõlbustab ka arvutusi. Einstein ütleb vaid seda, et me võime seda fiktsiooni ka edaspidi kasutada, kuid peame aduma, kui kaugele ta kõlbab ja mõistma, et erinevatel vaatlejatel võib ta isemoodi välja tulla.

Võidakse küsida: "Milleks küll muretseda nende paranduste pärast, kas ei piisa meile siis sellest pildist, mida me tegelikult näeme?" Vastust pakub käsilolev näide: mõtleme vaid, mida näeksid meie kaks vaatlejat, kui nad heidaks pilgu auto tagaosa poole.

Siis on kõik ümber pööratud, auto ulatub uksest läbi, ja uks asub auto tagumise poole keskel. Nii on see ikka: valguse kiirusele lähenevate kiirustega objektid, mis mööduvad vaatlejast küllalt ligidalt, näivad äärmiselt moonutatud. Juba möödunud osa näib kokku surutud, lähenev osa – välja venitatud. Seda seepärast, et näeme objekti kaugemaid osi sellistena, nagu nad olid varemalt. Kui nad liiguvad teie poole, näete neid kaugemal, kui nad teist eemalduvad, siis lähemal. Jüri näeb auto tagumist poolt neli korda pikemana kui eesmist poolt! Juta näeb jällegi garaaži samaviisi moonutatult.

Nähes neid moonutusi, eelistaksid nad ilmselt relativistlikke parandusi. See, mida nad näevad, on hoopis erinevam mõistlikust tegelikkusepildist kui parandatu. Einstein vähemalt laseb autol säilitada püsikuju!

Õieti öelda Einstein lihtsalt nihutas piiri selle vahel, mis on meist väljaspool ja mis seespool, meie peas. Varasemate teadlaspõlvkondade meelest võinuksid joonise 9-4 pildid ja parandatud asendid tabelis 10-2 näida sama reaalsetena kui vaatlusedki. Einstein taipas, et nad on ainult leppeliselt õiged, seda vaid meelevaldselt valitud taustsüsteemis. Kui kasulik ka ei oleks taustsüsteemi mõiste, ei tule see mitte loodusest, vaid meie vermime selle endale.

Peagi näeme, et on veel üks võimalus tegelikkuse esitamiseks. See on neljamõõtmelise aeg-ruumipilt. Intuitiivselt pakub too vähem rahuldust kui meie tavapildid, kuid tema eeliseks on see, et kõik vaatlejad võivad temaga ühtviisi nõustuda.

Meil on jäänud teha veel vaid üks samm relativistlike teisenduste arendamises: väljendada ajavahemik teises taustsüsteemis sündmuste vahel, mis on esimeses taustsüsteemis samaaegsed. Kui ühe vaatleja meelest toimus sündmus pikkuse L võrra eemal, läbis signaal seda ajavahemiku

jooksul. Selle aja sees liikus teine vaatleja teepikkuse vT. Seega kummagi vaatleja hinnagud ajavahemikule, mil signaal on teel, peavad erinema selle aja võrra, mis ta läbib lisateed vT. Jagades selle pikkuse c-ga, saame

Kaht sündmust, mis on üheaegsed taustsüsteemis, mis liigub teie tausta suhtes kiirusega v, eraldab teie taustsüsteemis ajavahemik t. c² tõttu nimetajas on see ajavahemik üldiselt väga lühike. Kuid valguse kiirustele lähenevatel kiirustel võib vahe muutuda üsnagi märgatavaks. Seda illustreerib hästi kaksikute paradoks, millega tutvume selle peatüki lõpul.

Einsteini esimesed artiklid relatiivsusteooriast olid nii põhjalikud, et teistel ei jäänud enam suurt midagi lisada. Erandiks oli vaid Hermann Minkowski, Einsteini Zürichi-aegne õpetaja.

Minkowskit häiris Einsteini käsitluses see, et üksainus realiteet võimaldas erinevaid kirjeldusi. Ta oli kindel, et asju peab saama esitada ka teisiti, tegelikkusele lähedasemalt. Ta leidis, et selleks tuleb käsitada aega, justkui see oleks ruumi neljas mõõde.

Sõnake justkui on siin oluline. Minkowskile ei tulnud pähegi väita, et aeg ja ruum on kaotanud kumbki oma identiteedi. Ta leidis vaid, et relatiivsuspostulaadist järeldub seos aja ja ruumi vahel, mis on analoogiline, kuid mitte identne seosega ruumi eri mõõdete vahel.

Ruumis on mõõtmed seotud Pythagorase teoreemi kaudu. Kui punkt on meist 3 km ida pool ja 4 km põhja pool, saame kauguse temani linnulennult, võttes

Kui objekt on ka meist erineval kõrgusel, tuleb lihtsalt juuremärgi alla lisada kolmanda mõõtme ruut.

Õigeid tulemusi annab see arvutus ainult siis, kui me mõõdame "põhja", "itta" ja "üles" samades ühikutes. Et käsitada aega neljanda mõõtmena, peame esmalt teda mõõtma pikkusühikutes. See on üsna lihtne: korrutame lihtsalt aja kiirusega c, et saada kaugust, millele valgus selle ajaga levib. Astronoomid kasutavad alatihti vastupidist teisendust, väljendades kaugust mingi täheni valgusaastates.

Minkowski leidis, et aega võib küll lisada Pythagorase valemisse, kuid eriviisil, mis meenutab, et meil ei ole tegemist lihtsalt veel ühe ruumimõõtmega. Selle asemel, et liita tema ruutu ruumidimensioonide ruutudele, tuleb see lahutada! Nõnda toimides saame suuruse, mis jääb samaks kõikides taustsüsteemides.

Meenutame näiteks rongi pikkuse mõõtmist 9. peatükis. Rongi taustal vaadeldi mõlemaid telefoniposte samal ajal, Maa taustal oli kahe vaatluse vahel ajaline viivis. Sellest johtus, et kaugus L kahe posti vahel ületas L₀-i, seisva rongi pikkust. Minkowski reegli järgi tuleb meil Maa süsteemis lahutada (ct)² L²-st. Rongi taustsüsteemis on ajavahemik null, seega aegruumiline intervall S on võrdne L₀-ga:

Sedaviisi saavad mõlemad vaatlejad nõustuda, et neljamõõtmelises aegruumis on kaugus mõlema vaatluse vahel L₀. Sõitjate meelest olid vaatlused üheaegsed, kaugus on rongi pikkus. Mida aga rongisaatjad nimetavad lihtsalt pikkuseks, on raudteevahile kombinatsioon pikkusest ja ajavahemikust.

Kui rong on 1000 meetrit pikk ja liigub kiirusega 0,6c, siis Maa süsteemis eraldab poste γ × 1000 = 1250 meetrit. Kasutades eelmises alalõigus saadud valemit, leiame ajavahemiku t = 1250 × 0,6/c = 2,5 μs (mikrosekundit). Korrutades c-ga, teisendame selle pikkuseks, saame 750 meetrit. Seega saab raudteevaht aegruumiliseks kauguseks (intervalliks)

s.o. seisva rongi pikkuse.

Tegelikkuse algelement neljamõõtmelises maailmas on sündmus, miski, mis juhtub teatud kohas ja ajal. Rongisaatjate postitäheldused olid kaks sellist sündmust. Kombineeritud neljamõõtmeline aeg-ruumiline vahemik (intervall) kahe sündmuse vahel jääb samaks kõikides taustsüsteemides, seepärast nimetatakse teda invariandiks. Rongi süsteemis olid mõlemad täheldused üheaegsed, ajavahemik nende vahel null ja sündmusi eraldab rongi pikkus. Maa süsteemis peab raudteevaht arvestama nullist erinevat ajavahemikku, siis saab ka tema tulemuseks rongi seisupikkuse. Rongi "kokkutõmme" on tema taustsüsteemi eriomadus, see pole invariantne ega kuulu meie neljamõõtmelisse pilti.

Mõistagi tuleb meil selle eelise eest maksta. On peaaegu võimatu kujutleda neljamõõtmelist maailma. Teda saab käsitleda üksnes algebrasümbolite varal. Seepärast suhtuski näitmudelite küljes rippuv Einstein alguses Minkowski ideesse tõrjuvalt. Ent taibanud eeliseid, võttis ta selle kahel käel vastu ja püüdis just sedakaudu avardada oma teooriat uutele nähtustele (lähemalt peatükis 12).

Relatiivsusteooria üllatuslikkust aitab süvendada meie ruumi- ja ajatunnetuse järsk erinevus. Silm võib eristada esemeid mõne sentimeetri kaugusel või haarata laiu vaatevälju palju kilomeetreid eemal. Kuid võime vaevu kujutleda tühiseid tuhandiksekundisi ajavahemikke, mis kuluvad valgusel selliste kauguste läbimiseks. Seepärast pole meil vajadust aiva meeles pidada, et me ei näe kaugeid esemeid praegusel hetkel. Kui meil oleks kogu aeg tegemist asjadega, mis tormavad valguselähedaste kiirustega, peaksime tingimata arvestama vüvitusi ja relatiivsusteooria näiks meile loomulikuna.

Meie harilik tegelikkusetaju sarnaneb filmiga. See on seeria kaadreid, mis näitavad sündmusi eri kohtades järjestikustel ajahetkedel. Raskusi teeb see, et eri filmid on tehtud erinevates taustsüsteemides. Mõlemad sisaldavad samu sündmusi, kuid need, mis on ühes süsteemis samadel kaadritel, võivad teises sattuda eri piltidele. Lisades neljanda mõõtme, paneme kõik sündmused ühele suurele pildile, millel on adekvaatselt esitatud aegruumilised seosed asjade vahel. Paraku on see pilt algusest peale abstraktne.

Käsitades aega neljanda dimensioonina, peame silmas pidama eesmärki. See on lihtsalt raamatupidamisvõte, mis lubab paremini arvet pidada kiirete objektide üle. Garaažiparadoks näitab, et ei see, mida me näeme, ega ka kolmemõõtmene pilt, mille konstrueerime viiviseid arvestades, pole täiesti rahuldavad. Neljamõõtmelisel pildil on uste avanemiste ja sulgumiste vahel sama vahemik, pisut alla 20 aegruumi jala, vaatamata taustsüsteemile.

Selle leppe taustal saab valguse kiirus pelgalt aja ja ruumi ühikute teisendusteguri tähenduse, justkui 2,54 oleks teisendustegur sentimeetrite ja tollide vahel. See arusaam on nüüd nii tavapärane, et ta on jäädvustatud koguni mõõdusüsteemis. Praegu võime aega mõõta ühe sajatriljondiku täpsusega. Pikkuste mõõtetäpsus ei pääse selle lähedalegi. Seepärast ei hoolitagi enam pikkuse etalonist. Rahvusvaheline Mõõtude ja Kaalude Büroo on võtnud aluseks valguse kiiruse täpseima väärtuse, 299792458 m/s, ja kuulutanud selle standardiks. Meeter defineeritakse nüüd kui kaugus, mille valgus läbib 1 /299792458 sekundiga. Michelson võiks pettumustki tunda, et pole enam põhjust üha korrata tema lemmikkatset, valguse kiiruse mõõtmist. Selle tulemus on alaliseks fikseeritud rahvusvahelise kokkuleppega.

Galilei relatiivsusõpetus annab lihtsa eeskirja kiiruste teisendamiseks ühest taustsüsteemist teise. See on lihtlabane liitmine. Kui ese liigub kiirusega u taustsüsteemis, mis kulgeb kiirusega v teie suhtes, näete teie teda liikuvat kiirusega

On selge, et relatiivsusteooriasse see valem enam ei sobi. Muuhulgas lubaks ta U-l kasvada üle c. Vastav relativistlik valem peab arvestama nii aja kui pikkuse teisenemist. Tulemuseks on

Sellest valemist johtub kaks olulist järeldust:

1. Kui kas u või v on palju väiksem kui c, on Galilei valem ligikaudselt õige.
2. Kui u = c, tuleb ka U = c. Seda pole raske näha, tehes selle asenduse ja korrutades nii lugejat kui ka nimetajat oga. Mõistagi on see sama, mis relatiivsuspostulaat kinnitab: kui kiirus on c ühes taustsüsteemis, on ta seda ka teises.

Kui nii u kui ka v on mõlemad võrdsed ½c-ga, leiame valemist, et U ei ole mitte c, nagu Galilei järgi tuleks, vaid 0,8c. Näidetes, kus uurisime rakette, mis liiguvad üksteise suhtes kiirusega 0,6c taustsüsteemis, kus mõlemad liiguvad üksteisele vastu, ei tuleks vastuliikumise kiiruseks mitte 0,3c, vaid ½c.[*[Asendage valemisse v  = ¹⁄₃c ja u =  –0,6c; saame U = –¹⁄₃c.]*]

Üht relatiivsusteooria kõige kummastavamat ennustust illustreerib järgmine ulmelooke.

Noor astronaut asub teekonnale tähe juurde, mis asub 25 valgusaasta kaugusel. Tema kosmoselaeva kiirus on 99,98% valguse kiirusest, mis annab Lorentzi teguriks 50. Astronaudil on kaksikvend, kes jääb koju Maale. Viiskümmend aastat on möödunud. Maine vennas, juba hallipäine, läheb kosmodroomile tervitama kosmoseseiklustest naasvat venda. Reipalt hüppab trapilt ikka nooruslik kaksikvend: astronaudi elus on möödunud vaid üks aasta!

Maale jäänud kaksikvenna vaatekohast on põhjuseks see, et aeg ise on tähelaeval aeglustunud. Niihästi mehaanilised kellad kui ka bioloogiline kell – vananemisprotsess on ülikiires kosmoselaevas aeglustunud ühe viiekümnendikuni oma normaalsest käigutempost. Astronaudile endale näib aga kõik korras olevat. Tema meelest liikusid Maa ja täht, kaugus nende vahel kahanes poole valgusaastani, nii et edasi-tagasi teekonnaks valgusligidasel kiirusel kulus parajasti aasta. Kuid mõlemad on ühel meelel selles, et astronaut on nüüd 49 aastat noorem kui ta kaksikvend!

Relatiivsusteooria algaastail pakuti seda lugu teooria ümberlükkamiseks. Miks pole Maale jäänud kaksikvend noorem? Lõppude lõpuks pidi astronaudi seisukohast aeglustuma Maale jäänud kell! Siin näib ilmnevat vastuolu.

Vastus peitub selles, et astronaut ja tema vend on eristatavad. Astronaut pidi tegema läbi kiirenduse meeletu kiiruseni, et lahkuda Maalt tähelennule ja siis tähe lähedal ümber pöörama, mis tähendab uut kiirendusperioodi. Seega ei olnud ta konstantse kiirusega ühtlases liikumises. Relatiivsuse sümmeetria, mis lubaks tal pidada maist kella aeglustunuks, pole enam rakendatav. Üksikasjalik analüüs näitab, et astronaudi vaatevinklist pidi suurem osa viiekümnest aastast Maal mööduma selle lühikese ajaga, kui ta tegi tagasipööret

Et paradoksi lahendus peitub just siin, võib taibata, kui kujutleme, et varem on tähe ümber tiirlema saadetud tehiskaaslane, millel on kell seatud Maa aega näitama. Kuna astronaut peab nü seda kella kui ka Maale jäänud kella liikuvateks ajanäitajateks, käivad nad tõesti üpris teosammul. Kuid kuna täheligidane kell on näiva liikumise joont mööda palju tagapool, on ka see Maa kellast ees. Valemis

on L 25 aastat korda c, ja v ainult pisut vähem kui c, seega on lugeja 25c². Astronaudi arvates on see kell umbes 25 aastat Maa ajast ees.

Kui astronaut jõuab täheni ja käivitab oma reaktiivmootori, et peatuda ja siis tagasi pöörduda, muudab ta olukorra vastupidiseks. Kaks Maa aega näitavat kella liiguvad nüüd vastassuundades, kusjuures liikvel on see, mis Maale jäänud. Seega on nüüd Maa aeg 25 aastat ees tähekella näidust. Kui eemal Maal olev kell hüppas olekust ~25 aastat taga seisu ~25 aastat ees, peab Maal olema möödunud ~50 aastat lühikese pöördeaja jooksul. Seepärast jääb astronaut kasikvennaga nõusse: Maal on möödunud palju enam aega kui ruumilaeval, ja tema on nüüd umbes 49 aastat vennast noorem.

See 50 aastane hüpe Maa ajas tekkis seepärast, et astronaut muutis teekonna keskel taustsüsteemi. Relatiivsusteooria oma algkujul ei suuda seda eriefekti seletada. 12. peatükis naaseme uuesti selle juurde, sest ta on üks neid lahtisi otsi, mis sundisid Einsteini minema senikäsitletud teooriast edasi.

Tänapäeval on kaksikute paradoks saanud lahutamatuks osaks meie ajateenistuse tavatehnoloogiast. Maailma ajateenistus rajaneb aatomkelladel, mis töötavad tseesiumiaatomite kimbul. Nende mõõteviga on mõni nanosekund ööpäevas. Kuid raadio teel antavaid ajasignaale võib usaldada üksnes kümnendik-millisekundi täpsuseni: raadiolainete teekond atmosfääris pole sirgjooneline ja seda ei saa täpselt määrata. Et teised kellad käiksid ühte maailma etalonkelladega, saadetakse portatiivsed aatomkellad teele lennukitel. Arvestades täpselt lennuki teekonda, tehakse relativistlikud ajaparandused, mis pikal lennul võivad ulatuda kümnete nanosekunditeni. Selle protseduuri kontrolliks saatis Ühendriikide Mereobservatoorium (Naval Observatory) 1972. a. kellad ümberilmalennule, võrreldes neid hiljem Washingtoni jäänud kelladega. Tulemused kinnitasid relativistlikke ennustusi.

Ulmekirjanikud on laialt kasutanud kaksikute paradoksi kirjanduslikke võimalusi. Üks lugudeseeria kujutab aega, mil inimkond on hajutatud asustatavatele planeetidele üle kogu Galaktika. Tsivilisatsiooni mõõtmed on paisunud üle tuhandete valgusaastate. Astronaudid ajavad oma võimsate kiirrakettidega äri selle hiigeltsivilisatsiooni saarekeste vahel, ise mõistetud veidrasse eksistentsi, milles nad naasevad kodusadamaisse 189 Robert H. March alles seal möödunud sajandite või koguni aastatuhandete järel, nautides normaalse eluea piires võõristavat poolsurematust.

Relatiivsusõpetus pakub kaht liiki leevendust konfliktsetele piltidele erinevates taustsüsteemides. Üks seisneb ühest süsteemist teise teisendamise eeskirjades, teine konstrueerib uue esitusviisi, millega kõik saavad nõusse jääda. Teisenduseeskirjad sisaldavad 8. peatükis sisse toodud Lorentzi tegurit g. Aja ja pikkuse teisenduste näidetest ilmneb, et need annavad pilte, mis erinevad vaid vaadeldamatute omaduste poolest. Uus esitusviis seisneb selles, et aega käsitatakse formaalselt nagu. see oleks ruumi neljas mõõde. Siit johtub kaks asja: ajad teisendatakse kaugusteks, korrutades neid valguse kiirusega, ja rakendatakse Pythagorase lauset. Aja ja ruumi erisuse vääramatust näitab see, et Pythagorase valemi ruutude summasse ajadimensiooni ei liideta, vaid lahutatakse. Kui see on sooritatud, jääb aegruumiline distants (intervall) kahe sündmuse vahel samaks kõikides taustsüsteemides. Analüüsisime ka tuntud kaksikute paradoksi, milles astronaut võtab ette pika edasi-tagasi kosmoserännaku valguslähedasel kiirusel ja naaseb tublisti nooremana kui tema kojujäänud kaksikvend. Tuli välja, et paradoksi lahendab asjaolu, et astronaut muudab oma taustsüsteemi rännaku keskel.

What is matter? – never mind.
What is mind? – it doesn't matter.[*[Sõnademäng, tõlkesumbes: Mis on aine? – pole lugu. Mis on lugu? – pole tähtis.]*]
ANONYMOUS

Einsteini lihtsa postulaadi omaksvõtmine on pannud meid maksma ränka tribuuti. Eksperimendid näitavad, et meil ei jää üle muud kui realtiivsusteooriaga leppida. Kuid see sunnib meid tavamõistuse kallal lausa metsikusi sooritama. Oleme pidanud otsustavalt muutma oma arusaamu ajast ja ruumist. Kuna need mõlemad on aluseks liikumise kirjeldamisel, võib oodata sama drastilist vägivalda ka Newtoni füüsika kallal. Kas tõesti peame maha kriipsutama kahesajandilise edukäigu, minema pühkima Newtoni seadused, energia ja impulsi jäävuse ja kõik seonduva?

Muidugi mitte. See pole ka ime, sest pidagem meeles, et Einsteini lähtepunktiks oli nimelt säilitada üht Newtoni füüsika rünnatavat põhijoont, nimelt inertsiaalsete taustsüsteemide ekvivalentsust. Suurem osa Newtoni ehitisest jääb seisma ka pärast Einsteini pöördelist sekkumist.

Tõsi, see sekkumine ei jäta kõike muutusteta. Põhilised muutused koonduvad massi mõistele. Ilmselt on Newtoni esimene ja kolmas seadus puutumatud. Kui me aga ei rõhuta, et mehaanika käsitleb liikumise muutusi, mida põhjustavad kehade vastastikmõjud, ei jää alles midagi, mille tõi sisse just Newton. Selgub, et impulsi jäävust ja Newtoni teist seadust saab päästa, kui laseme massil sõltuda kiirusest meile juba tuttava Lorentzi teguri kaudu. Mis puutub energia jäävuse seadusse, siis leiame, et see sõltuvus viib massi ja energia kaksiklusele, mida väljendab XX sajandi füüsika kõige tuntum valem

Kummatigi ei pane selle peatüki väited teie usaldust sellisele proovile nagu eelmise peatüki omad, sest nende järeldused ei paista niivõrd meeletud.

Püüame kõigepealt selgitada, kuidas mass sõltub kiirusest. Teeme seda mõttelise katse kaudu, milles laseme kaldu põrkuda kahel ühesugusel kosmoselaeval. Sellist põrget tunneb iga piljardimängija. Liikuva keha suund ei muutu kuigivõrd ja kiirustki kaotab ta vähe, aga pihtasaanu läheb aeglaselt liikvele algliikumisega peaaegu ristsuunas. Joonis 11-1 näitab, kuidas asi paistab kosmoselaevade meeskondadele.

Asjast saame aru paremini, kui vaatame ainult liikumise komponenti, mis on risti algselt liikuva keha suunaga. Selles suunas meil pole muret pikkuste ebakõladega. Silmas tuleb pidada ainuüksi liikuva kella efekte. Ja juba Galilei andis meile õiguse vaadelda liikumise ristuvaid komponente üksteisest eraldi.

Küsime, mida peame omaks võtma, et säiliks impulsi ristsuunaline komponent. Laseme kummalgi meeskonnal käivitada stopperi põrkehetkel ja mõõta, kui kaua läheb aega, et pihtasaanu eemalduks ristsuunas kaugusele x. Sümmeetriast järeldub, et stopperid kummaski laevas annavad sama näidu t ja mõlema laeva reisijad määravad kiiruse ristkomponendi ühtviisi. Kuna laevad on võrdse massiga, saavad mõlemad ka võrdse impulsi väärtuse 

Näib, nagu oleks kõik kombes, kuid peame meeles pidama, et kumbki meeskond ei pea teise mõõdetud aega kehtivaks oma taustsüsteemis. Kumbki korrutab t kohe läbi γ-ga. Kumbki lisab γ laeva impulsi nimetajasse, rikkudes niiviisi impulsside tasakaalu. Et seda taastada, on vaja γ-t ka lugejasse. Kuna kauguse x suhtes ollakse ühel nõul, pole seda tegurit võimalik lisada kuhugi mujale kui massile. 

Siit järeldub, et impulsi jäävus jääb jõusse vaid siis, kui kiirel kehal on rohkem massi kui aeglasel. Samal viisil saaks arutleda ka liikumissuunas, kuid arvutus oleks keerukam. Niisiis, kui räägime massist, peame kaasama sümboli m₀, et märgistada paigaloleva keha massi. Relativistlikku massi defineerib valem

Nagu seisupikkus L₀ nii on ka seisumass m₀ invariant. Mass m on seevastu määratud ainult ühes kindlas taustsüsteemis.

See modifikatsioon ei muuda massimõiste olemust. Ta jääb ikka "kalduvuseks vastu seista liikumise muutustele". Meid ei peaks liigselt hämmastama see, et kiired kehad on liikumise muutustele tõrksamad kui aeglased. Veelgi enam, see nähtus sõlmib kinni ühe lahtise otsa, mis jäi ripakile juba 9. peatükis: miks on c absoluutne piirkiirus?

3. peatükist lugesime, et Newtoni teine seadus määratleb jõu kui impulsi ülekande kiiruse. Kuna impulsi muutusi ei kutsu tavaliselt esile mitte massi, vaid kiiruse muutused, võib kirjutada valemi F = ma. Kuid relatiivsusteoorias on muutlikud nii kiirus kui ka mass. Newtoni definitsioon jääb jõusse, kuid lihtne valem taandub lähenduseks väikeste kiiruste puhul, kui γ ei muutu kiiresti.

Kiirenegu keha paigalseisust püsiva jõu mõjul. Alul muutub mass üpris vähe, kogu impulsi muutus johtub kiiruse muutusest. Kui aga kiirus läheneb valguse kiirusele, saab keha üha massiivsemaks ja tõrgub aiva enam kiirust muutmast. Impulss kasvab küll samas tempos edasi, kuid enamik sellest muutusest läheb massi kasvu arvele, kürus kasvab ülivähe.

Lähenedes valguse kiirusele, pürib Lorentzi tegur lõpmatusse. Mass saab kiirendusele ületamatuks barjääriks. Osakeste kiirendites mõjutavad võimsad elektromagnetjõud elektrone või prootoneid. Aastaks 1996 oli ühes neist masinaist saavutatud osakese kiirus 0,999999999987c. See rekordkiirendi (LEP – Large Electron-Positron [Accelerator]) töötab Genfi lähedal Šveitsis. See on 23 kilomeetrine ring magneteid ja vaakumtorusid, mis läks maksma enam kui miljard dollarit. Kui küllalt tugev või küllalt kestev tõuge suudaks kiiruspiirangut ületada, oleks see temp ammugi tehtud.

Võidakse küsida, mida siis need kiirendid õieti teevad? Kindlasti pole kogu see raha ja pingutused kulutatud selleks, et saada mingit tühist kiiruse kasvikut. Elektrijõud annab osakesele ikka edasi impulssi, tehes tööd. Töö läheb energiaks. Selle energia nähtavaks märgiks on just massi kasv. Elektronid LEP-i pöörises on 200 000 korda raskemad kui seisvad.

Siit järgneb sügavam ja üldisem järeldus: kõikidel energialiikidel on ka mass. Massi kasv kiirusega on vaid selle erijuht.

Saab näidata, et elektroni kallal tehtav töö LEP-is on just tema massi muutus korda c ruudus. Kuid energia jäävus käib liikumise enda kohta. Seepärast tuletagem seos massi ja energia vahel mõttelisest katsest, mis rõhutab energia jäävust.

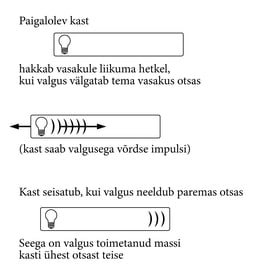
Peatükis 6 näitasime, et elektromagnetjõudude puhul on impulsi ja energia jäävus täidetud vaid siis, kui omistame neid kumbagi ka väljale endale (siis muidugi ka valgusele). Kui miski kiirgab valgust ühes suunas, peab ta saama tagsilöögi vastassuunas. Maxwelli teooria annab lihtsa seose valguse energia ja impulsi vahel: E = pc. Impulsi definitsiooni järgi p = mv. Kuna kiirus von siin valguse kiirus c, võime kirjutada p = mc ja asendada selle Maxwelli seosesse. Saamegi 

Kuna meil on tegemist valgusega, mida siis siin see mass tähendab? Ons ta midagi enamat kui matemaatiline fiktsioon? Vaatame joonist 11-2. Suletud kastis, mis hõljub ilmaruumis, on vasakus otsas patareitoitel välklamp. Laseme tal välgatada. Kui seejuures impulss säilib, peab kast veidi vasakule põrkuma. Valgusvälge neeldub kasti paremas otsas. Valguse impulss antakse kastile tagasi, kast seiskub.

Algul seisev kast nihkus vasakule, ilma et temale oleks mõjunud mingi välisjõud. Kuid see on ju täpselt sama, kui teatav mass oleks kastis liikunud vasakult paremale!

Võidakse vaielda, et katse näitab üksnes seda, et valguse abil võib teisaldada massi, mitte mingit üldist seost massi ja energia vahel. Kuid vaatame kasti olekut pärast peatumist. Valgust pole enam ollagi. Kübetki kasti materjalist ei kõrvaldatud vasakult ega viidud paremale, kuid ometigi transpordid massi tema kahe otsa vahel! Mis on veel muutunud? Mis jääb näitama valguse ülekannet?

Vastus: neeldunud valgus soojendas kasti parempoolset otsa. Teisipidi, vasakus otsas võeti energiat patareist. Vasakus otsas muundati teatav hulk keemilist energiat elektrienergiaks, edasi valgusenergiaks, ja lõpuks soojuseks paremas otsas. Samal ajal teisaldati massi vasakult paremale. Tähendab, kõik need energiavormid peavad täitma massi-energia seost. Tühjenenud patarei peab olema kergem laetust, kuum ese peab olema raskem kui sama ese külmast peast. Kuna soojus pole midagi muud kui molekulide liikumisenergia, peab seegi rahuldama seost massi ja energia vahel. Tänu energia jäävuse seadusele laieneb massi ja energia ekvivalentsus mistahes energiavormile.

Tuleb rõhutada, et

on relatiivsusteoorias üks ja ainus energiavalem. Mis saab siis meie endisest kineetilise energia määratlusest ½mv², mis peaks madalatel kiirustel ikkagi toimima? Vastuseks on, et kineetiline energia esitab üksnes aeglaselt liikuva keha massi pisikest juurdekasvu. Meenutame γ ligikaudset valemit 8. peatükist, mis kehtib väikestel kiirustel. Korrutades m₀c²- ga saame

Liige m₀c² kannab seisuenergia nime, see on energia, mis objektil on paljalt tema olemasolu tõttu. See peegeldab asjaolu, et aine tekitamine nõuab energiat. Teine liige on kineetilise energia tuttav definitsioon, liikumisest tulenev lisaenergia.

Pole kohatu küsida, kuidas valgus võib levida kiirusega c, kui tal on mass. Vastame: kogu valguse mass on "kineetiline", tal pole üldse seisumassi.

Hulkade teadvuses on see valem Hirošimast peale ikka olnud seotud tuumaenergiaga. Ometi tuleb alla kriipsutada, et see valem kehtib ühtviisi kõikide energialiikide jaoks. Universaalne ja ainulaadne, on ta jõus nii lõkke kui tuumarelva puhul. Tuumaenergia erisus seisneb vaid selles, et see on ainus energialiik, mille puhul massimuutused on tegelikult märgatavad.

Kui vett soojendada külmumispunktist keemistäpini, kasvab tema mass vaid ühe sajamiljardiku ehk 10^–11 osa võrra. Tavalises keemilises reaktsioonis, näiteks põlemisel, on põlemisproduktid kulutatud kütusest ja hapnikust kergemad miljardikosa (10^–9) võrra. Nii väikesed muutused pole muidugi mõõdetavad. Hoopis ägedamates tuumareaktsioonides leiavad aset juba tuhandikulised massimuutused. Kui füüsikul on käepärast tuumamasside tabel, võib ta Einsteini valemi järgi ennustada, kui palju energiat vabaneb seni uurimata tuumareaktsioonides.

Tuumaenergeetika ja tuumarelvade arendamises oli otsustav tuumalõhustumise ahelreaktsioonide avastamine. Nendes vallandab iga lagunev tuum laguprotsessi mitmetes naabertuumades. Valem E = mc² ei vihjanud üldse selliste reaktsioonide olemasolule. Pole tal tähtsust ka nende mõistmisel. Einsteinil polnud mingit osa ei tuumalõhustumise avastamises ega aatomipommi valmistamises, välja arvatud tema allkiri president Franklin D. Rooseveltile adresseeritud kirjal, mis hoiatas aatomipommi valmistamise võimalikkuse eest ja viitas Saksamaa pingutustele selle loomiseks. Kui selleks ajaks olnuks relatiivsusteooria veel loomata, poleks see tõenäoselt oluliselt pidurdanud Manhattani projekti edu.

Vahel peetakse seda valemit ekslikult energia massiks muundamise valemiks. Tegelikult on ta midagi enamat. Ta väidab, et praktiliselt kõikidel juhtudel on need kaks identsed. Kõikidel energiavormidel on ka mass ja see, mida tavatseme massiks kutsuda, nüüd siis seisumassiks, on vaid üks energiavorm. See on täiesti loomulik arendus XIX sajandi mõtetele energia säilivusest.

Kui näiteks lõke põleb kinnises kastis, mis omab täiuslikku soojusisolatsiooni, ei saa kasti kaal muutuda. Sellele vaatamata, et keemiline energia muundub soojuseks, mis esindab molekulide soojusliikumise energiat, ei muutu mass. Kui aga soojus kandub väljapoole, jääb kast õige pisut kergemaks.

Olgu massi ja energia ekvivalentsuse üldise kehtivuse viimaseks näiteks selle rakendus potentsiaalse energia juhul. Kui jõud seob kaht objekti, on nende ühendmass väiksem eraldi võetud masside summast. Negatiivne potentsiaalne energia ilmneb massidefekti kujul. Tuumaenergia tegelik allikas on nende võimsate jõudude potentsiaalne energia, mis seovad tuumaosakesi ühte. Suure nõrgalt seotud tuuma ümberkorraldus väiksemateks, kuid tugevamini seotud tuumadeks suurendab seosejõudu ja vähendab tuumade massi. Kuna see mass on ühtlasi välja energia, on ta ruumis jaotunud. Mida enam välja kontseptsioon füüsikas küpseb, seda enam lisandub talle omadusi, mida harjumuslikult seostame ainega.

Tüüpiline tuum "kaalub" umbes 0,8% vähem kui teda moodustavate osakeste masside summa. Aatomipommi õudustäratav vägi tuleb sellest, et raskeimad tuumad kaaluvad umbes 0,1% tuumaosakese kohta rohkem kui nende elementide tuumad, mis paiknevad perioodsustabeli keskosas, ja veel lõhustumisprotsessist, mis killustab teatavad rasked tuumad väiksemateks osadeks, kusjuures vabaneb tuhandikosa massist soojusena.

Väljaspool tuuma on massidefektid sootuks väiksemad. Näiteks kaalub vesinikuaatom ainult 1/600000 võrra vähem kui tema koostisosad prooton ja elektron kokku. Päikesesüsteem on umbkaudu triljondiku võrra kergem kui Päikese, planeetide ja teiste tema ümber tiirlevate kehade üksikmasside summa.

Energia ja massi ekvivalentsus illustreerib veel kord valguse kiiruse kui muundusteguri osa suuruste vahel, mida alul peeti täiesti erinevaiks. Oleks seda ekvivalentsust adutud algusest peale, polekski vahest kummagi jaoks eraldi ühikuid. Elementaarosakeste füüsikud kasutavadki päevast päeva massi jaoks energiaühikuid, sest gramm on nende jaoks päratu suur. Sellest seisukohast on c² midagi taolist kui teisendustegur 0,621 kilomeetritest miilide saamiseks.

Kummatigi on valguse kiiruse ruut üpris suur teisendustegur. Energia ei kaalu palju. Et saada kilogramm energiat, läheb

džauli! Pommid,mis hävitasid Hirošima ja Nagasaki, kaotasid kumbki umbes ühe grammi massi, et teha oma pöörast purustustööd.

Üks kilogramm energiat on parasjagu niipalju, kui suuremad soojuselektrijaamad toodavad aastas soojusena. Elektriks muundub sellest umbes kolmandik. Tuumajaamas tuleb see kilo ligikaudu 1 tonni lõhustuva tuumakütuse kulutamisest. See tuleb omakorda kütusekomplektist, mis kokku kaalub umbes 50 tonni. Kivisöekütusel elektrijaam annab sama energiahulga ligemale miljoni söetonni varal, see teeb enam kui 150 kilomeetrit söeronge aastas.

Massi sõltuvus kiirusest oli üks esimesi relatiivsusteooria ennustusi, mis sai katsekinnituse. Elektronid on nii kerged, et neid on hõlpus ülinobedaks kiirendada. Teleri kineskoobis tormavad nad umbes veerandiga valguse kiirusest. Siis on nende mass ligi 3% suurem seisumassist. Pole raske saavutada ka kaugelt suuremaid kiirusi. Elektronide massi kasvu mõõdeti juba 1906. aastal. Energia ja massi seos tuumareaktsioonides leidis kinnitust 1932 esimesel tuumade tehislikul lõhustamisel.

Nüüdseks on kõik relatiivsusteooria väited eksperimentaalselt sedastatud. Elementaarosakeste füüsikud töötavad päevast päeva objektidega, mille kiirus läheneb valguse omale. Põrgetel toovad need osakesed ilmsiks kõikide Einsteini ennustuste paikapidavuse. Nii näiteks on mõned osakesed nii lühiealised, et lagunevad aja jooksul, mis kulub valgusel mõne sentimeetri katmiseks. Et nad aga liiguvad lähi-valguskiirustel, võivad nad raskusteta jõuda meetrite kaugusele tänu oma "sisekella" käigu aeglustumisele.

Osakese vaatekohast ei johtu see efekt ajakulu aeglustumisest, vaid laboratooriumi kokkutõmbest. Lõpptulemus on sama: nad jõuavad registreerimisseadmesse. Ja kui paigalseisus väga kerge osake tormab suure kiirusega, toimib ta põrgetel raske partiklina. Osakese kiirenemisel saadud lisamass võib kuluda uute osakeste tekitamiseks, mida enne olemaski polnud.

Relatiivsusteooria lõppvõiduks oli Faraday ja Maxwelli töö lõpetamine elektri ja magnetismi ühendamisel. Einstein näitas, et kui liikuv vaatleja seirab puht-elektrivälja, ilmneb magnetväli, ja vastupidi, kui liikuvast vaatepunktist vaadelda magnetvälja, tekib elektriväli.

Einstein tundis Newtoni vastu sügavat austust ning juba loomu poolest oli talle igasugune revolutsioonilisus üpris vastumeelne. 1905. aasta artiklid relatiivsusteooriast säästsid Newtoni füüsikat, sõnastades selle ümber viisil, mis oli kooskõlas Maxwelli valgusõpetusega. Kuid Einstein jõudis edasi sügavama ja veelgi pöördelisema kaemuseni. Pärastpoole hakkas ta nimetama teooriat, millega oleme senini tutvunud, erirelatiivsusteooriaks. Aastal 1915, pärast kaheksa-aastast heitlust valemitega, saatis ta maailma teooria, mille nimetas üldrelatiivsusteooriaks. See laiendas relatiivsusprintsiipi üksteise suhtes kürenevalt liikuvatele taustsüsteemidele ja hõlmas ka gravitatsiooni.

Einsteini sihiks oli füüsika selline ümbersõnastus, et jõu mõiste sellest sootuks kaoks. Gravitatsiooni kirjeldas ta kui ruumi enda koetise moonutust, mis vüb selleni, et sirge lakkab olemast lühim tee kahe punkti vahel.

Just üldrelatiivsusteooria ajendas sageli korrutatud (kuid üdini vale) jutu, et vaid tosin inimest maailmas saab sotti Einsteini vaimusünnitustest. Tegelikult said sajad füüsikud ja matemaatikud Einsteinist aru tema teooriate ilmumise päevil, tänapäeval mõistavad seda tuhanded. Kuigi ta rajaneb ülikeerukal matemaatikal, ei ole üldrelatiivsusteooria põhimõtted põrmugi rasked ega ähmased. Võtame nad kõne alla järgmises peatükis.

Vaatamata aja ja ruumi relativistlikule ümbertõlgendusele säilib impulsi jäävus, kui eeldada, et mass kasvab koos kiirusega võrdeliselt Lorentzi tegurile. Siit johtub iseendast relativistlik kiirusepiirang, sest valguse kiirusel peab mass kasvama lõpmatuks. Käsitledes valgust suletud kastis, saime seose E = mc² energia ja massi vahel. Kuigi rahva hulgas seostatud tuumaenergiaga, rakendub see valem kõikidele energiavormidele, tähendades lihtsalt, et energial on mass. Ta on energia jäävuse seaduse loomulik edasiarendus.

Igas lihalikus olendis uinub kasutamatult, varjatult, tajumatult ja tundmatult Lõpmatu Aru. Kuid igavik on määranud ta lõpuks ärkama, rebima endalt aistiva tunnetuse viirastusliku võrgu, purustama alatiseks oma lihaliku tupe ja tormama vallutama Aega ja Ruumi.  LAFCADIO HEARN, Teemandilihvija

Kord 1907. aasta sügisel rabas tollast Šveitsi Patendibüroo teise klassi tehnilist assistenti Albert Einsteini miski, mida ta hiljem on nimetanud "minu elu kõige õnnelikumaks mõtteks". Ta enda jutustuse järgi oli see nii.

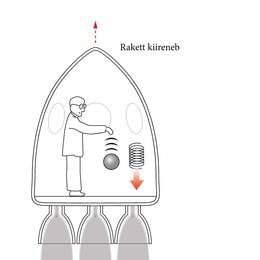
Istusin oma toolil Berni Patendiametis, kui mulle tuli äkitselt pähe niisugune mõte: "Kui keegi langeb vabalt, ei tunne ta omaenda kaalu." Olin üllatunud. See lihtne mõte jättis minusse sügava mulje. Ta tõukas mind gravitatsiooniteooria poole.

Kohe ei saanud sellest õnnelikust mõttest siiski midagi. Tema ja eesmärgi vahele astus kaheksa aastat eksirännakuid ja taasalustamist aga ka matemaatilise aparaadi loomine, mis kuulub kõige pöörasemate hulka, mis iganes leiutatud.

Tegelikult Einstein vaid "taasavastas" Galilei vaba langemise seaduse: kõik kehad langevad võrdse kiirendusega. Kui keegi langeb vabalt kinnises kabiinis (või sns tiirleb Maa ümber, mis on vaba langemise erijuht), langeb kõik kabiinis olev samakiirendusega. Pole vähimatki suhtelist liikumist, mis näitaks gravitatsiooni olemasolu. Tänapäeval, mil oleme harjunud televisiooni otseülekannetega mehitatud kosmoselaevadelt, tundub see meile endastmõistetav, kuid toona pidi selleks kujutlust pingutama.

Et seletada gravitatsiooni sellest küljest, luges Newton jõu võrdeliseks massiga. Kuid Einstein teisendas massi määratlust. Sellest sai suurus, mis erines eri taustsüsteemides. Polnud sugugi selge, kuidas see mõjub Newtoni gravitatsiooniseadusele. Edasi, gravitatsiooniseadus tuli ümber formuleerida Newtoni hetkelisest kaugmõjust väljaks, mille levi piirab valguse kiirus. Ja lõpuks pidi gravitatsioonivälja energial endalgi olema mass. Polnud põrmugi selge, kuidas kõige sellega toime tulla. Vähemasti oli tal üks selge pidepunkt, iga uue teooria katsekivi: Galilei seadus pidi kehtima jääma. Niisama kui relatiivsuspostulaati püstitades valis Einstein taas selle põhiseaduse oma teooria loogiliseks lähtepunktiks, mitte lõppsihiks.

Einsteini õnnelikemast mõttest järeldub loomulikult ka vastupidine: ühtlaselt kiirenevas suletud kabiinis näib mõjuvat gravitatsiooniväli. Joonisel 12-1 on rakett kaugel maailmaruumis. Reaktiivmootorid on käigus. Mistahes lahti lastud keha selles hakkab ühtlaselt kiirenevalt "langema" raketi saba poole. Newtoni käsituses ei mõju kehale mitte mingit jõudu. Tegelikult kiireneb ju rakett. Sellest ka kõikide kehade ühesugune kiirendus – raketi kiirendus. Kiirenevas taustsüsteemis toimib automaatselt Galilei seadus.

Einstein seadis eesmärgiks luua ühtne teooria, mis rakenduks ühthästi nii kiirenevates taustsüsteemides kui ka gravitatsiooniväljades.

Et jõuda oma gravitatsiooniteooriani, mida ta nimetas üldrelatiivsusteooriaks, lisas Einstein relatiivsusteooriasse veel teise postulaadi:

Mitte ühegi ühes kohas tehtud katsega ei saa eristada gravitatsioonivälja kiirenevast taustsüsteemist.

Sõnad "ühes kohas" on olulised. Einstein ei välistanud kõiki erinevusi gravitatsiooni ja kiirenevate taustsüsteemide vahel. Kui võrdleme esemete langemist eri kohtades Maa peal, siis leiame, et kõik nad pürivad maakera keskpunti poole. Seda moodust ei jäljenda ükski kiirenev taustsüsteem, kuigi pöörlevas süsteemis on kiirendus suunatud teljest eemale. Einstein ütleb vaid seda, et kõik esemed reageerivad gravitatsiooniväljale samal moel kui kiirenevas taustsüsteemis olekule.

Nagu juhtus juba erirelatiivsusteoorias, toob see näiliselt lihtne hüpotees, mis on tuntud ekvivalentsusprintsiibina, kaasa ootamatuid järeldusi. Enne kui asume neid uurima, täpsustame oma eesmärgi ja selleni jõudmise raja.

Arutluste lõpuks jõuame järeldusele, et pole mingit vajadust gravitatsioonijõu järele. Langevate kehade või planeetide kiirenemine on lihtsalt inertsiaalse liikumise erijuht: kehad kulgevad mööda lühimaid võimalikke teid. Ainult need teed pole mitte sirgjooned, sest aegruum ise ei ole tasane!

Nende sõnadega on see häda, et me ei suuda kuidagi kujutleda, mida nad tähendavad. Pole meil kerge sedagi omaks võtta, et maapind on kumer. Vaadates tasapinnalist kaarti, on raske uskuda, et lühim tee kahe punkti vahel maapinnal, matemaatilise nimega geodeetiline joon, on tegelikult kõver.

Kuid ikkagi võime uskuda, et Maa asub täiesti tasases ruumis ja kui saaksime temast tunneli läbi puurida, oleks see lühim tee. Kuid ruum ise on kõver? Mis on nende sõnade taga?

Üritame seda salapära hajutada juba läbiproovitud mõtteliste katsetega. Järjekorras peaksid nad näitama järgmist.

1. Kiirenevas taustsüsteemis on aegruum kõige labasemal viisil kõver.
2. Valgus kulgeb mööda kõverjooni kiirenevates süsteemides ja seega ka gravitatsiooniväljas.
3. Kui soostume, et see tähendab, et aegruum ise on kõver, seletub gravitatsioon täielikult, ilma et kordagi tuleks meenutada jõudu. 
4. Gravitatsioon mõjustab aega, moondades 50 aastase ajahüppe kaksikute paradoksis tõsinähtuseks. 
5. Inimesed, kes elavad ümaras maailmas, kuid usuvad selle olevat tasase, peavad leiutama jõude nagu gravitatsioon.
6. Kõik ülaltoodu on tõestatud ohtrate katsete-vaatlustega; on olulisi nähtusi, mida ei saagi teisiti seletada.

Tasuks sellest tihnikust läbimurde eest saame füüsika, milles on mõningaid hämmastavaid veidrusi nagu mustad augud. Lisaks saame kujutluse Universumi päritolust.

Liiklusreeglid on sellel teel lihtsamadki kui erirelatiivsusteoorias. Tuleb vaid möönda, et kui miski võib juhtuda kiirenevas taustsüsteemis, peab see juhtuma ka gravitatsiooniväljas.

Joonise 12-2 oleks võinud väga hästi sehkendada ka Galilei ise, tundnuks ta vaid graafikute joonestamist, mille leiutas Descartes. See aga on enam kui graafik. Meie vastses neljamõõtmelises keeles on see aegruumi kahemõõtmelise vülaku kaart, mis näitab kas kiirenevas süsteemis või gravitatsiooniväljas vabalt kulgeva eseme teekonda. Silmnähtavalt on see kõverjoon.

Newton oleks kohe küsinud, kas siis siin tegelikult gravitatsiooniväli mõjub või mitte. Kui mõjub, on teejoon tõesti kõver. Kui mitte, siis näeme lihtsalt sirgjoonelist teed kõveraks moonutatult, vaadeldes seda kiirenevast süsteemist. Einsteini jaoks on see vahetegemine ilma igasuguse tähenduseta. Igal juhul allub ese inertsiseadusele, nõnda kui see rakendub kohalikus taustsüsteemis. Siin on inertsiaalsed trajektoorid kõverad ja kõik.

Vaatame nüüd, kuidas oleks lugu valgusega. Kujutleme end joonise 12-1 raketti. Laseme selles ristipidi laserikiire seinast seina. Kuna vastassein kogub kiirust sellal kui valgus on teel, jõuab kiir seinani sihtpunktist allpool ja valguse teekond läbi raketi on tegelikult parabool. Ekvivalentsuse printsiibi kohaselt on gravitatsiooniväljas sama lugu.

Kõverus on nii väike, et selle tuvastamisega jääme kimpu. Kujutleme, et hästi selgel päeval läkitame valguskiire ühelt mäetipult teisele, mis on 30 km kaugusel. Valgus jõuab sinna kümnetuhandik-sekundiga. Selle ajaga läbib langev keha vahemiku, mis vaid väheke ületab aatomi läbimõõtu. Me ei suuda iganes kindlaks teha, et kiire tee kõverdub sirgjoonest nii tühiselt kõrvale.

Selles näites pole veel midagi, mis häirinuks Newtoni unerahu. Oma teises kuulsaimas raamatus, Optikas, arvas temagi, et gravitatsioon võiks mõjutada valguskiire teed. Tegelikult käib vaidlus selle üle, kuidas keegi kirjeldab nähtava põhjust. Vaatame kõigepealt tavalist langevat keha, et mõista, kuidas Einstein seletab tema liikumist.

Nüüd võidakse vastu vaielda, et säärane tühine kõverus vaevalt küll seletab langevate kehade liikumist. Kummatigi tuleb meeles pidada, et kõver ei ole mitte lihtsalt ruum, vaid aegruum. Kõveruse märkamatajäämine on veelgi üks järeldus meie ruumija ajataju disproportsioonist.

Kui pillame peost mündi, jõuab see põrandale umbes poole sekundiga. Peame seda lühikeseks ajavahemikuks, kuid tema ruumivaste neljamõõtmelises pildis on tohutu. Valgus katab sellega umbes 150 000 kilomeetrit. Joonise 12-2 kohaldus mündile oleks graafik, mis püstsuunas ulatub meetri kõrgusele, ent rõhtsuunas laiub 150 000 kilomeetrini. Oleme lõiganud päratu kahemõõtmelise viilaku neljamõõtmelisest aegruumist ja selle tühine kõverus on küllaldane seletamaks mündi liikumist.

Einsteini järgi pillatud münt lihtsalt järgib oma loomulikku kõverdatud teed aegruumis. Oma pika teekonna järel jõuab ta põrandapunkti aegruumilise teekonna joonele. Too on sirge, sest mitte kõike ei otsusta gravitatsioon. Mis ka ei annaks tahkele ainele jäikust, peab see suutma mõjutada ka aegruumi geomeetriat. See võib ületada gravitatsiooni ja sirgestada põranda rada aegruumis.

Newtonil ja Einsteinil ei teki lahkhelisid nende aegruumi teede kirjeldamises. Erinevad vaid kõverduspõhjuste seletused. Newton ütleks, et teid kõverdab jõu mõju. Einstein väidaks, et mingit jõudu pole vaja, sest aegruum ise on kõver.

Nüüd oleme teinud kolm esimest, kergeimat sammu oma arutlusplaanist, aga ikka ei mõista teha valikut gravitatsiooni njutoniaanliku ja relativistliku seletuse vahel. Lahenduse toovad ülejäänud kolm.

Oleme nüüd valmis üle selgitama segadust astronaudiga kaksikute paradoksis. Joonisel 12-3 on kiirenev rakett, mille ninas on kell, mis saadab kümme korda sekundis ajasignaale, mida raketi sabas vastu võetakse.

Rakett kiireneb, sellal kui signaalid on teel vastuvõtjani, kogub ta täiendavalt kiirust, suundudes signaalile vastu. Oletame, et ta saab juurde ühe kümnendiku valguse kiirusest. Lisades selle liikumise signaalide endi kiirusele, osutub, et vastuvõtja saab ühe täiendava signaali igas sekundis. Tuleb välja, et meil on kell, mis saadab kümme signaali sekundis, kuid vastuvõtja, mis saab neid üksteist.

Kuidas on see võimalik? Ei toodeta ju teel lisasignaale! On vaid üks pääsetee: nõustuda sellega, et sekund raketi sabas erineb sekundist tema peas. Kuna vastuvõtja saab 10% rohkem signaale, kui saadab kell, peab tema sekund olema 10% pikem. Seega käib kell raketi sabas 10% aeglasemalt kui kell raketi ninas. Ekvivalentsuse printsiibi kohaselt peab olema samuti gravitatsiooniväljas.

Et mõista, kuidas see aitab astronauti oma loost välja tulla, leiame kella aeglustumise valemi. See on lihtsalt raketi kiiruse juurdekasvu, mille ta saab signaali teeloleku vältel, ja valguse kiiruse suhe. Kui kiirendus on a ja püstise raketi kõrgus h, läheb ajavahemikus t ülemine kell alumisest ette

võrra.

Maa gravitatsiooniväljas on a võrdne raskuskiirendusega g (umbes 10 m/s²). Meie valemi nimetajas on hiigelnumber c², seega tuleb δt imeväike. Kui viia kell õhupallil 10 km kõrgusele, hakkab ta tunnis ette käima ainult 4 nanosekundit.[*[Valem kehtib ainult Maa raadiusest palju väiksemate kõrguste jaoks. Vastasel korral tuleb arvutada valemi

järgi.]*]

Kui lühike see aeg ka poleks, aatomkelladega saab seda mõõta. Tavalise reaktiivlennuki kiirendus annab umbes sama suure ajakao. Seepärast tuleb aatomkellade ümberilmareisil arvestada mõlemat efekti.

Kaksikute paradoksi astronaudi puhul on efekt juba vägagi tuntav. Selleks, et muuta valguslähedast kiirust mõne päevaga vastassuunaliseks, peab kiirendus miljardeid kordi ületama raskuskiirendust Maal. Seejuures on Maa "ülessuunas" kvadriljoneid meetreid eemal. Niisiis peab raketi pöörde jooksul kulgema Maa aeg palju kordi kiiremini kui aeg raketis. Kuna raketimootorite käigus olles seal ülikaugel ei saanud see mõjutada aega Maal, peab astronaut järeldama, et tema jaoks oli aeg pöörde jooksul "kinni külmutatud" ja viiskümmend aastat möödusid tema jaoks väga lühikese aja jooksul.

Tema kojujäänud kaksikvend võib nüüd vaid sõnada: "Minu meelest on sinust küll üsna veider kasutada säärast totrat taustsüsteemi, kuid ma pean nõustuma, et sinu seletus, olgu see nii imelik kui tahes, on vähemalt seesmiselt kooskõlaline." Märgime, et siin ei ole tegemist kahe vaatlejaga, kellest kumbki arvab, et teise kell jääb maha. Kumbki möönab, et kiirenevas taustsüsteemis sõltub kella käik selle asukohast ja "kõrgemal" olevad kellad käivad kiiremini.

Ärge liigselt muretsege selle pärast, kui te veelgi ei suuda hoomata kõverat aegruumi. Mõelge vaid, et veel nüüdki on inimesi, kes usuvad, et Maa on tasapinnaline!

Laseme kahel neist tumedatest inimlastest alustada reisi põhja suunas. Las üks alustab teisest 100 km ida pool, kusjuures mõlemad kulgevad sama kiirusega. Meie, kes usume ümarasse Maasse, teame, mis nendega juhtub. Nende teed lähenevad kogu aeg üksteisele, kuni nad lõpuks põhjapoolusel kokku saavad.

Kui nad teel olles kogu aeg jälgivad oma vahekaugust, ilmneb, et alul on lähenemine üsna aeglane, lõpupoole aga lähenemiskiirus muudkui kasvab. Seega siis kiirenev liikumine! Kui nad jonnakalt jätkavad tasapinnalise geomeetria rakendamist, ei taipa nad kuidagi, mis siis on untsu läinud. Üks võimalus oleks arvata, et neid lükkas üksteise poole mingi jõud. Nende "kiirendused" ei sõltu massist nagu gravitatsiooni puhulgi, seega peaks see jõud olema massiga võrdeline.

Näitasime lihtsustatult, milleni viib aegruumi kõveruse eiramine. Et asja kujuteldavaks teha, piirdusime kahe mõõtmega, meie planeedi kõvera pinnaga. Näitest puudus ajadimensioon. Et seda korvata, asendasime aja harjumuspärase ühtlase kulgemise rändurite ühtlase edasiliikumisega. Muus osas on analoogia täielik.

Et siiamaani jõuda, vajas Einstein abi. See tuli tuntud kandist. Kõverpindade geomeetria kuulub raskeimate matemaatikaosade hulka. Einsteini koolitusest jäi siin vajaka. Aastal 1912, kui ta naasis Prahast Zürichisse, et asuda oma alma mater´is professoritoolile, läks ta oma vana sõbra Grossmanni juurde, kes oli samas matemaatikaprofessoriks. "Grossmann," anus ta, "aita mind, muidu ma lähen arust ära!"

Õnneks oli ravim käepärast. Viiskümmend aastat varem oli matemaatik Bernhard Riemann loonud geomeetria, mis täpselt passis Einsteinile. Ta oli väljendanud isegi arvamust, et tasuks uurida meie ruumi geomeetriat suurtes mastaapides, et selgitada, kas see ikka on eukleidiline. Kuigi Grossmann polnud ses valdkonnas kodus, ta vähemalt teadis, et Riemanni geomeetria on olemas. Mõneks kuuks ühendati jõud, kuni Einsteini lahkumine Berliini taas koostöö katkestas. Kuid sellestki piisas, et juhtida viimast õigele teele.

Abi oli üpris teretulnud, sest sel ajal ei töötanud Einstein enam üksinduses. Tema teooriad olid algkujul trükist ilmunud. Jäi vaid nendest loobuda, kui nad poleks hakanud toimima. Ta jooksis võidu teistega, kellest mõned, nagu matemaatikud David Hilbert ja Emmy Noether, olid sedasorti matemaatikaga temast hoopis paremini kursis. Kuid sellest hoolimata jäi ta võitjaks tänu oma hiilgavale füüsikatajule ja erakordsele keskendumisvõimele.

Saime selgeks, et ruumi kõverus Maa lähedal on liiga väike, et avaldada mõõdetavat mõju valguskiirtele. Päikese gravitatsiooniväli on tublisti tugevam, vähemalt tema läheduses. Joonis 12-4 näitab, mis juhtub tähe näiva asendiga, kui tema valgus peab Päikesest lähedalt mööduma, et meieni jõuda.

Ruumi kõverus Päikese ligiduses on küllaldane, et kallutada valguskiirt 1,7 nurgasekundi võrra. Olgu see nurk küll tilluke, kuuemeetrise pikkusega teleskoobis vastab ta süski tähe kujutise 0,05 millimeetrisele nihkele, mis jääb headel fotoplaatidel mõõtetäpsuse piiresse.

Muidugi oleks ka Newton lootnud näha taolist nihet. Tõepoolest, aastal 1801 arvutas astronoom Johann von Soldner Newtoni gravitatsiooniseaduse põhjal valguse kiirusel liikuva eseme tee, kui see möödub Päikesest viimase pinda puudutades. Tema sai hälbeks 0,84 sekundit. Einstein polnud sellest tööst kuulnud ja kordas 1911. a. Soldneri tulemust. Ta arvutas tookord valguskiirte hälvet tänu gravitatsioonilisele kellaefektile tasases, eukleidilises ruumis. Siis ta veel ei teadnud, et aegruum on kõver. Kõveras ruumis on efekt kaks korda suurem, nii et Einsteini gravitatsiooniteooria õigsuse näitamine nõuab umbes poolesekundiliste nurkade usaldatavat mõõtmist.

Tähtede pildistamine Päikese lähedal on muidugi võimalik ainult täieliku päikesevarjutuse ajal. Loomulikult peab ka teleskoop olema viidud täisvarju piirkonda. Toetudes Einsteini reputatsioonile, suundus Saksa ekspeditsioon 1914. aastal Krimmi täielikku päikesevarjutust pildistama. Paraku jäid pildid tegemata: varjutuse ajaks olid Saksamaa ja Venemaa juba sõjajalal ja astronoomid jäid ajutisse sõjavangi kui vaenuriigi alamad.

Aasta hiljem oli Einsteinil juba oma teooria kujundatud. Selle alusel tegi ta ka uue ennustuse, mille järgi hälbenurk kahekordistus. Kui Saksa ekspeditsioon oleks korda läinud, oleks Einsteini õigele teooriale juhtinud tema varasema ennustuse ootamatu nurjumine. Kuid siis oleks ka mõnevõrra tuhmunud ta aupaiste. Einsteinil oli taas õnne.

Esimene maailmasõda hakkas juba lõpule jõudma, kui briti astronoom Arthur Eddington sai Einsteini uuest ennustusest kuulda neutraalse Hollandi kaudu. Tekkis võimalus kahe teooria laupvastanduseks, ja see lõhnas ajaloosündmuse järgi. Ta sedastas kohe, et 1919. a. kevadel on täielik päikesevarjutus nähtav Atlandi lõunaosas. Edasi, varjutuse ajal pidi Päike asuma Hüaadide tähtkujus, tihedas täheparves, milles on hulgi heledaid, varjutuse ajal hästi nähtavaid tähti. See oleks kontrolli täpsust tublisti tõstnud.

Ekspeditsioonid saadeti nii Aafrikasse kui ka Lõuna-Ameerikasse: Eddington ei tahtnud riskida sellega, et pilvitus võinuks temalt au röövida. Kui fotosid võrreldi varasematega, milles Päike polnud mängus, leidis Einsteini ettekuulutus kinnituse.

Nüüd, raadioteleskoopide ajastul, oleme märksa õnnelikumas seisus, sest Päike on suhteliselt nõrk raadiotäht ja pole enam vaja varjutusi oodata. Alates seitsmekümnendatest aastatest on tehtud korduvalt mõõtmisi ja iga uus täpsustus kinnitab Einsteini tulemust üha paremini.

Niipea kui Eddington oli tulemuses kindel, edastas ta uudise, jällegi Hollandi kaudu, Berliini. Einstein suhtus sellesse oma tavalise külma rahuga. Kui tema sekretär küsis, kuidas ta oleks end tundnud, kui ennustus osutunuks valeks, vastas ta: "Siis oleks mul armsast Issandast kahju olnud, sest teooria on õige!"

Newtoni gravitatsiooniteooria sai veelgi tõsisema löögi, kui väike kosmoselaev Mariner 9 saadeti 1972–1973 tiirlema Marsi ümber. Ta oli tolle planeedi esimene tehiskaaslane. Tema pardal oli seadis, mis peegeldas tagasi Maalt saadetud radarisignaale. Kui Maaja Marsi ühendussirge läheb Päikese lähedalt, lisandub joonisel 12-4 visandatule uus, ajamõõde. Radarisignaal läbib tee Maalt Marsile umbes 20 minutiga.

Eukleidese tasases ruumis on arvutused lihtsad. Tuleb joonestada signaali kõverdunud tee tasapinnale ja leida, kui palju pikem on see sirgest. Selgub, et umbes 10 meetrit (30 jalga), järelikult peaks signaal saabuma 30 nanosekundit hiljem, kui võiks arvata Maa, Marsi ja kosmoselaeva teadaolevate asendite järgi.

Paraku on see hinnang Einsteini kõveras aegruumis sama kasutu, kui katse leida New Yorgi ja Londoni täpset vahekaugust mõõtmistega tasapinnalisel kaardil. Päikese lähedal aeg aeglustub, elektromagnetsignaal saab täiendava viivise. Kõvera aegruumi valemitest tuleb ajaviivis 200 mikrosekundit, mis on üle 6000 korra rohkem kui tasase ruumi puhul. Uurimisrühm Massachusettsi Tehnoloogiainstituudist Irwin Shapiro juhtimisel leidis, et õige on pikem viivis.

Nüüdseks on loodud teisigi gravitatsiooniteooriaid peale Einsteini oma. Võib-olla ei võidakski Einsteini teooria lõplikul iludusvõistlusel. Kuid kõik sõelale jäävad on kõvera aegruumi teooriad. Tasase ruumi teooriate aeg on läbi.

Kõvera aegruumi omaksvõtuga on mehaanikateadus taandunud puhtaks triviaalsuseks. Füüsika kaob, jääb vaid geomeetria. Liikumisseadusi pole enam vaja, jääb vaid ainus tõdemus:

Kõik esemed liiguvad mööda kõvera aegruumi geodeetilisi jooni.

Või nagu sõnastas Ameerika füüsika teoreetik John Archibald Wheeler, "aine ütleb ruumile, kuidas kõverduda, ja ruum ainele, kuidas liikuda."

Kuid milline geomeetria! Et saada aimu, kui keeruline ta on, arutleme nii. Et iseloomustada ühemõõtmelise joone kõverust mingis punktis, on tarvis vaid üht arvu, kõverusraadiust. Kahemõõtmelist lehte saab painutada kahes suunas, kusjuures nende suundade vahel võib olla suvaline nurk. Tema kõverust saab väljendada kolme numbriga. Kuigi me ei suuda kujutleda, kuidas näevad välja kõverdunud kolme- ja neljamõõtmelised ruumid, teame, mitu numbrit vajame nende kõveruse täpsustamiseks: vastavalt kuus ja kümme.

Kümme numbrit! Newtoni gravitatsiooniteooria sai hakkama vaid ühe numbriga, mis näitas jõudu. Ilmselt on Einsteini teooria palju keerulisem. Selle kirjeldamiseks tarvitseme hirmus ränka matemaatilist keelt, tensor-diferentsiaalgeomeetriat.

Enamikuks praktikajuhtudeks teda tema keerukuse tõttu ei sünni kasutada. Tema osa füüsikas sarnaneb püha tekstiga, mis on salajas enamuse eest ja mida vaid kõrged preestrid usutalitustel avavad. Teda tarvitatakse, et kontrollida valemeid, mis kõlvulised lihtolukordades, või siis ligikaudseid valemeid, millest tulenevad kõvera aegruumi efektid kui väikesed parandused Newtoni gravitatsiooniseadusele.

Ärge lootkegi, et intuitsioon võiks olla usaldatav teejuht kõveras neljamõõtmelises maailmas. Te põrkute inimese kesknärvisüsteemi sadade miljonite aastate pikkusele evolutsioonile. Silmad on meie täiuslikemad meeleorganid ja aju on kohanenud töötlema silmitsi saadud teavet Eukleidese geomeetria kohaselt. Võime hoomata Maa kahemõõtmelise pinna kõverust üksnes tänu kolmandale mõõtmele, millesse ta saab painduda. Ekslik oleks arvata, et kui neljamõõtmeline aegruum on kõver, siis peab olema ka viies mõõde, millesse ta kõverduda saab. Kogu lugu on üksnes ülalmainitud kümnes numbris. Pole vaja mingit välistausta. Ruum, mille oleme konstrueerinud, on olemuslikult ja kaheldamatult kõver.

Uue geomeetrilise ilmavaate viimase tehtena torkame sisse massi ja energia ekvivalentsuse ja vaatame, mida imet see kaasa toob:

1. Kõver aegruum näitab välja olemasolu.
2. Väljad salvestavad potentsiaalset energiat.
3. Energial on mass.
4. Mass on gravitatsioonivälja allikas, niisiis – punkti 1 tagasi!

Kui kaugele on viinud meid Faraday jõujoonekesed! Nad said alguse sellest, et taheti vältida kaugmõju probleemi. Nüüd tekitavad nad ise mateeriat. Ühtaegu moodustavad nad aegruumi koe.

Alustasime füüsikast, mis nõudis nelja tõelusevormi: ruumi, aega, mateeriat ja liikumise põhjust, alul jõudu, siis energiat. Erirelatiivsusteooria lõi sideme aja ja ruumi ning aine ja energia vahel. Nüüd on ühtlustus täielik:

Mateeria on energia on aegruum.

Neis mõnes sõnas on küllalt harmooniat, et võluda mõnd zeni guru. Kuid imetledes selle maailmapildi kristalset lihtsust, mõelgem ka sellele, mille jaoks ta polegi nii täiuslik. Ta pole ülesande terviklik lahendus, vaid pigem projektülesanne, raam, millesse suruda meie pilt Universumist. See pilt ei ole täielik, sest gravitatsioon ei ole ainus maailmas eksisteeriv väli. Oma elu viimased 25 aastat veetis Einstein üritades elektromagnetismi oma geomeetriasse sisse viia. See ei läinud tal korda.

Aine ehitust ohjab elektromagnetism ning teised jõud, mis toimivad subaatomilises mõõtkavas. Universumit ei saa mõista, mõistmata aatomit.

Nüüdisfüüsika sai alguse gravitatsiooni uurimisest. Tema esimene saavutus lahendas vaidluse selle üle, kas Maa liigub. Nüüd, Einsteini teooria valguses, võime väita, et kogu vaidlus läks aia taha! Einstein ei tunnusta mingeid eesõigustatud taustsüsteeme. Vähemalt põhimõtteliselt saab seletada kõiki Päikese ja planeetide näivaid liikumisi taustsüsteemis, milles Maa on paigal. Sama käib kogu ülejäänud kosmose kohta. Ometigi oleks säärase aegruumi geomeetria kohutavalt väändunud. Einstein ütleks: "Olgu, jäage oma Päikese-keskse süsteemi juurde. Siis on geomeetria Eukleidese omale lähedasem." See, mis oli põhimõtte küsimus, on nüüd saanud pelgalt mugavusasjaks.

On kaks kenakest juhtu, mil aegruumi geomeetria annab täpseid lahendeid. Üks neist on Universum tervikuna, teine on hiiglaslik kerakujuline mass nagu Päike või Maa. Viimasest johtub üks üldrelatiivsusteooria kummalisimaid ennustusi, mida John Wheeler nimetas 1963. a. mustaks auguks.

Kujutlus mustadest aukudest on palju vanem kui nende nimi. Laplace osutas juba 1796. aastal, et kui täht on mõõtmeilt küllalt väike ja küllalt suure massiga, võib paokiirus tema pinnalt ületada valguse kiirust. Valgus ei pääse siis tähest välja, küll aga võib nii valgus kui aine sisse langeda.

Aastal 1916, paar kuud pärast seda, kui Einstein sai valmis üldrelatiivsusteooria, näitas Karl Schwarzschild, et sama efekt ilmneb ka selles. Selle teooria järgi ei lange küll valgus lihtsalt tagasi, vaid järgib kõverjoonelisi teid, mille mõõtmed on tähe omast väiksemad. Kuna valguse kiirus on kõikide kiiruste piiriks, ei saa mustast august mitte miski välja. Täht on igas suhtes aegruumist välja lülitatud.

Selleks vajalik aine tihedus on pöörane. Et Päike muutuks mustaks auguks, peaks ta diameeter olema mõni kilomeeter. Rõhk, mida tekitab tuumatuli ta südamikus, hoiab teda kokku langemast. Isegi siis, kui Päikesel tema tuumakütus lõpuks otsa saab, ei arvata, et ta moonduks mustaks auguks. Ta kahaneb aegamööda umbes Maa suuruseks valgeks kääbuseks.

Valge kääbus ei saa olla rohkem kui umbes 30% raskem Päikesest. Massiivsem täht kahaneb edasi, kuni muutub neutrontäheks. See on sisuliselt üksainus mõnekümnekilomeetrise läbimõõduga aatomituum. Too moodustis pöörleb nobedasti, kiirates elektromagnetlainete perioodilisi välkeid justkui tuletorn. Välked sisaldavad kõiksugu lainepikkusi raadiolainetest röntgenikiirteni. Kui Maa juhtub selliste kiirtevihkude teele, täheldatakse signaale, mis rütmiliselt korduvad nagu täppiskella tiksumine. Sellist taevakeha kutsutakse pulsariks.

Esimesed pulsarid avastas 1967 Jocelyn Bell, tollal alles üliõpilane, töötades Inglismaal Jodrell Banki raadioteleskoobiga. Sest ajast on neid leitud sadade kaupa. Neiu Bell arvas esialgu õhinal, et on püüdnud maaväliste tsivilisatsioonide signaale, mida saadavad "väikesed rohelised mehikesed".

Pulsarit võib kasutada kui väljaspool Päikesesüsteemi asuvat ülitäpset kella. See annab veel ühe võimaluse aja relatiivsuse järelekatsumiseks. Maa orbiit ei ole ring, vaid ellips, jaanuari alguses tuleb ta Päikesele kõige lähemale. See aeglustab maapealseid kelli kahel kombel: Maa liigub kõige kiiremini ja ta on Päikese gravitatsiooniväljas kõige päikeselähemas seisus. Gravitatsiooni toime on kaks korda suurem kui Maa liikumise mõju. Võrreldes aatomkelli Maal ühe eriti täpse "pulsarkellaga", sai see kõik kinnitust.

Neutrontähe tekkel vabaneb mõne sekundiga sama palju energiat kui seda annavad kõik meie Galaktika tähed kokku. Seeläbi "puhutakse" tähe väliskihid eemale. Neist saab helendav paisuv pilv, supernoova. Udukogu Krabi tähtkujus on jäänus Hiina astronoomide poolt 1054. a. vaadeldud supernoovast. Tema keskmes, samuti kui Tycho Brahe ja Kepleri silmatud supernoovade jäänuste keskpunktiski, asub pulsar. Supernoova, mida vaadeldi Suures Magalhäesi Pilves 1987, andis neutrontähe sünnist märku ka hiiglasliku neutriinode puhanguga. Neutriinodest tuleb juttu 19. peatükis.

Kui tähe mass ületab umbes 1,5 korda Päikese massi, ei saa neutrontäht enam gravitatsioonile vastu ja kollaps jätkub kuni musta augu tekkeni. Kuna selleks vajalik lisamass pole suur, võib arvata, et paljud supernoovad lähevad seda teed.

On selge, et musta auku avastada on äärmiselt raske. Parimal juhul võiksime leida mõne, mis imeb küllaldase kiirusega ainet endasse. Seda võiks täheldada, kui must auk kuulub kaksiktähte, milles tema partner on tavatäht. Must auk kisub endasse kuumi gaase kaaslase atmosfäärist. Hiidkiirendus langemisel sunnib gaasi valgust kiirgama. Mida suurem kiirendus, seda kõrgem on kiirguse sagedus. Musta augu gravitatsioon on küllaldane, et tekitada röntgenikiiri.

Neid saab täheldada üksnes Maa tehiskaaslaste paigutatud teleskoopidega väljaspool atmosfääri, mis "röntgenivalgust" tugevasti neelab.

Sedaviisi on leitud palju kaksikallikaid, mille üks komponent on raske ja nähtamatu. Need võivad olla kas neutrontähed või mustad augud. Nende toime järgi nähtava partneri liikumisele saab arvutada nähtamatu massi. Mitmel juhul on see tublisti üle neutrontähe massipiiri. Tõenäoselt on siis tegemist musta auguga.

Lisateavet pakuvad nn. aktiivsed galaktikad, mis saadavad tohutuid kiirgushulki ainetihenditest oma keskosas. Selle ainsaks mõeldavaks allikaks võiks olla päratu must auk, mille mass ületab saja miljoni kordselt Päikese oma. Meie kodugalaktika keset varjutavad tolmupilved. Astronoomid, kel on õnnestunud piiluda läbi selle hägu, väidavad nägevat vihjeid väiksematele mustadele aukudele Galaktika südamikus.

Niisiis võime olla kaunis kindlad, et mustad augud on üsna laialt levinud. Kuid seda, mis juhtub nende ligikonnas, ei saa kaugeltki pidada tavanähtuseks.

Aja suhe musta augu piiril ja väljaspool seda osutub lõpmata suureks! Soovitame lugejal millestki toekast kinni võtta, enne kui hakata mõtisklema selle pisukese kõmuteate tähenduse üle. Nimelt väljastpoolt vaadates ei saa must auk eales päris valmis! Viimane massiraas, mis tõukaks ta üle tekkeläve, jääb piiril kinni. Ometi jõuab ta mõne tuhandiksekundiga väga lähedale "päris" mustale augule, nii et "peaaegu" must auk käitub samuti kui täisküps.

Kuid see, mida näeb mustale augule langeja, on juba liiga rabav. Augu piirde ületamise hetkel välismaailm kiireneb pööraselt, lipsab läbi kogu oma ajaloo ja kaob olematusse! Mis puutub meie vaatlejast sõbra saatusse, siis selle peame küll jätma ulmekirjanike hooleks.

Võite üllatuda, et Universum tervikuna kuulub aegruumi geomeetria lihtsaimate objektide hulka. Seletus on lihtne: Universum on nii päratu suur, et üksiktähed ja isegi galaktikad on sama tühised kui aatomid. Võime mateeria jaotumust pidada ühtlaseks ja pidevaks.

Kui Einstein lahendas küsimust aastal 1915, sai ta üpris üllatava tulemuse: Universum ei saa olla staatiline. Ta peab kas paisuma või kokku tõmbuma. Tollal oli inimteadvusse tugevasti juurdunud mõte igavesest muutumatust Universumist. Einsteingi ei suhtunud tulemusse tõsiselt ja võttis valemis appi sobitusliikme, nn. kosmoloogilise liikme, et lepitada arvutusi staatilise Universumiga. Hiljem pidi ta seda nimetama oma "elu suurimaks veaks", sest 1927 näitas ameerika astronoom Edwin Hubble, et Universum tõepoolest paisub.

Hubble leidis, et kõik kauged galaktikad eemalduvad meie omast, justkui see oleks mingi kosmiline peletis. Mida kaugemal nad on, seda kiiremini nad eemale kihutavad. Üldrelatiivsusteooria õpetab, et mateeria ja aegruum on lahutamatud. Galaktikad ei haju lihtsalt lõpmatusse tühja ruumi, vaid ruum ise on lõpliku ulatusega, mis seejuures kasvab.

Joonise 12-5 õhupall näitab, kuidas see on võimalik. Olgu galaktikad täpid pallil. Kui pall paisub, eemaldub iga täpp oma naabreist. Mida kaugemale nad üksteisest jäävad, seda kiiremini nad eemale liiguvad.

Võrdlus on muidugi kahemõõtmeline. Ruumil on kolm mõõdet. Neljas mõõde, aeg, on paisumine ise. Neljandat ruumimõõdet ei ole olemas, meie kosmilisel õhupallil ei ole sisemust.

Gravitatsioonitõmbe tõttu see paisumine järk-järgult aeglustub. Kas siis lõpuks asendub paisumine ahenemisega? Seda me ei tea, sest meil puuduvad täpsed teadmised Universumi kogumassist. Laias laastus võib öelda, et nähtav mass ei saaks selle tembuga hakkama. Kuid kergesti võib olla ka nähtamatut massi, mis alles ootab avastamist.[*[Nähtamatu massi e. varjatud aine probleemiga on palju tegelnud ka eesti astrofüüsikud akadeemik Jaan Einasto juhtimisel – vt. nt. kogumik Universum, Tallinn 1998, lk. 36. (Tõlk.)]*] Tähtede liikumised galaktikates ilmutavad gravitatsiooninähteid, mis viitavad nähtamatu massi oreoolile, mis paljukordselt ületab nähtavat massi. Oma andami võivad anda nii mustad augud kui ka tundmatud kiirgusliigid. Universumi kogumassi näitav arv võib üksnes kasvada. Praeguste kõige optimistlikumate kogumassi hinnagute järgi peaks massi olema siiski umbes kümme korda vähem, kui tarvitsetaks pöördeks paisumiselt kahanemisele.

Sellest hoolimata püüavad paljud teadlased uskuda, et paisumine ükskord lõpeb. Seda suuresti seepärast, et alternatiiv - hajuda mittemillekski - pole põrmugi veetlev.

Projitseerides paisumise 12 miljardit aastat ajas tagasi, näeme Universumi sündi hiigelplahvatuses, mida kosmoloogid kutsuvad Suureks Pauguks. Kosmoloogid on spetsid kõigi asjade alguse üle mõtisklemise esoteerilises kunstis.

Siinkohal peame hoiatama. Enamikul teadusaladel välditakse spekulatsioone, mida ei saa katse ega vaatluse teel kontrollida. Paraku on usaldusväärseid vaatlusi, mis annaks teavet Universumi varajastest arengujärkudest, üpris vähe ja neid tehakse harva. Oleks ebainimlik vältida spekulatsioone millegi olemuselt nii lummava üle. Seepärast lendab kosmoloogias tavaline teaduslik ettevaatus aknast välja ja haaratakse ka kuitahes fantastiliste teooriate järele.

Kõik kiiresti paisuv peab jahtuma. Universum pole erandiks. Sündides pidi ta olema uskumatult tuline. Sellises seisundis juhib aine vabalt elektrit ja ei lase läbi mingit valgust. Sääraseks jäi Universum mõnesajaks tuhandeks aastaks. Viimaks küllalt jahtununa pidanuks valgus ja aine kokku andma ereda sähvatuse, mis peaks siiamaani uitama mööda Universumit. Seda ongi nähtud. Ta paistab täpselt sellisena, nagu seda ennustas 1948 vene päritolu ameerika füüsik George Gamow, kellest loeme lähemalt 17. peatükis.

Paisudes jahtub ka valgus. See tähendab, et tema lainepikkus suureneb. Tänaseks hõlmab see Suure Paugu kaja laineala mikromeetritest millimeetriteni infravalguse ja raadiolainete diapasoonis. Seda tuntakse 2,8 K taustkiirgusena, sest tema efektiivne temperatuur [*[Kiirguse efektiivne temperatuur tähendab temperatuuri, mille juures peaks olema keha, mille õõnsuses valdab vastava lainepikkuste koostisega kiirgus. (Tõlk.)]*] on 2,8 kelvinit (K), s.t. 2,8 sentikraadi (võrdne Celsiuse kraadiga) üle absoluutse nulli. Suure Paugu teooria viitab otse samale temperatuurile. Tema mõõtmisest tuleb lähemalt juttu 15. peatükis. Tõsiasi, et teooria seda nii täpselt ennustab, on samasugune määrav tõik, nagu Kuu kiirendus oli Newtoni gravitatsiooniteoorias.

On huvitav tõdeda, et 2,8 K taustkiirgus määrab taustsüsteemi, mida võib käsitada kui mõneti eelistatut. Kuigi seegi kiirgus levib sama kiirusega kõikides taustsüsteemides, on ometi vaid üks süsteem, milles teda tuleb igast suunast ühepalju, et koguimpulss jääks nulliks. Kui liigume selle tausta suhtes, siseneme liikumissuunas pisut suuremasse kiirgusvoogu. Seda on tõepoolest täheldatud ja selle põhjal võib väita, et selles süsteemis liiguvad Päike ja Maa kiirusega 600 km/s. Kui see süsteem oleks Michelsoni mõttes eelistatud, oleks ta kohanud kolossaalset efekti, neljakümne lainepikkuse suurust nihet.

2,8 K tausta teine oluline omadus on see, et ta ei ole mitte kõikides suundades täpselt võrdne. 1992. aastast peale tehtud täppismõõtmised on näidanud, et ta on pisut ebaühtlane. Ebaühtlus on üksnes 1 /100 000 tasemel. Tuleb välja, et see on väga hea uudis: ta näitab, et teda kiiranud aine ei olnud ilmaruumis päris ühtlaselt jaotunud.

Täiesti ühtlases ainepilves oleks gravitatsioon tirinud igas suunas ühtviisi. Siis ei oleks aine saanud koonduda kamakateks, millest lõpuks said galaktikad ja tähed. Et nende tekkeprotsess algaks, pidid olema tihedamad "idud", mille suunas sai tõmbuda aine naaberpiirkondadest.

Galaktikate tekkekiirus sõltub Universumi kogumassist. Mida rohkem seda on, seda tugevamad on gravitatsioonijõud ja seda kiiremini moodustuvad galaktikad. Esimesed galaktikad tekkisid mõne miljardi aasta jooksul pärast Suurt Pauku. Et nad üldse said tekkida neist tühistest ebaühtlustest, mida näeme 2,8 K taustkiirguses, pidi ainet olema hoopis rohkem, kui seda näha on. Veel üks vihje toetamaks neid, kes tahavad uskuda, et Universumi paisumine ei või kesta lõputult.

Kuidas aga jääb selle päris loomishetkega, kui meie Universum paiskus välja lausa geomeetrilisest punktist? Ja mis saab siis, kui paisumine seiskub ja kõik variseb tagasi garvitatsioonilises kollapsis, tohutus kosmilises kataklüsmis, Hiiglama Raksus? Võime vaid mõistatada. Kuid me teeksime seda märksa arukamalt, tutvunud kvantteooriaga, mikromaailma füüsikaga. Seepärast jätkem vahepeal see paeluv teema, et tulla tema juurde tagasi lõpupeatükis.

Nagu Newton enne teda, nii sai Einsteingi veel oma eluajal müüdiks. Ta on ainus XX sajandi teadlane, kelle näopildi igaüks sedamaid ära tunneb. Samuti kui Newtoni puhul, oli üheks ajendiks teadlaskogukonna tungiv vajadus leida kangelane, keda võiks eksponeerida laiale üldsusele. Einstein sobis sellesse rolli ideaalselt. Nii tema tagasihoidlikkuses, räpakas riietuses, äraolevas ilmes kui ka, ja eelkõige, tema soojas inimlikkuses kehastusid teaduse helgemad küljed.

Kuulsus tuli Einsteinile 1919, varjutuse-ekspeditsiooni jälil. Eddington oli meister avastust laiale hulgale suupäraseks maitsestama. Tookord oli tal ka poliitiline kirves ihuda. Maailmasõda oli teaduse rahvusvahelise koe tükkideks rebinud. Uute relvadega korraldatud veresauna järel olid teadus ja tehnoloogia vereplekkidega kaetud. Eelkõige oli teadusel vaja näidata maailmale oma palet humanistlikust küljest ja taaskuulutada traditsioone, mis seisid kõrgemal rahvaid üksteise vastu ässitanud väiklasest vihkamisest.

Päikesevarjutuse mõõtmised tehti teatavaks kõrgema näitekunsti hiilgeviisil. Rahvarohkel teaduskogunemisel Cambridge´i ülikoolis kuulutati täismajale, et Einsteinil oli õigus. Kõnetooli kohal kõrgus Newtoni büst ja Eddington pöördus dramaatilise žestiga selle poole. Paari järgneva päeva jooksul kirendasid maailma ajalehed sensatsioonilistest pealkirjadest, mis pasundasid revolutsioonist teaduses: "Kõik tähed taevas on kiivas... Miski pole seal, kus ta paistab olevat... Korrutustabelgi kahtluse all... Kuid ärge muretsege, dr. Einstein selgitab kõike."

Eddington uhkustas, et briti õpetlased olid rännanud tuhandeid miile, et kontrollida saksa kolleegi ideid. Ekspeditsioon võeti ette sellal, kui mõlemad rahvad olid veel ametlikult sõjajalal. Teati, et Einstein oli Saksamaal mõneti põlu all vastuseisu eest sõjale, samuti kui kveekerist Eddington Inglismaal. Maailm oli aldis sellistele sangaritele. Pealegi nägi Einstein välja nagu auväärne tark mägedest, kes mõistatab taevasaladusi.

Kuidas ka Einstein poleks ossa sobinud, loomuldasa ei kõlvanud see talle mitte. Oma parimaid töid tehes oli ta olnud tundmatu ja ta tundis oma üksildusest heameelt. Kuulsusega kaasnevad hüved ei vastanud tema pretensioonitule maitsele. Triumfaalse maailmaturnee lõpul, aastal 1921, mil ta sai Nobeli preemia, veeti Einsteini läbi Hispaania kuninga enda erivagunis. See tundus talle sedavõrd tülgastav, et ta jätkas teed Berliinini kolmandas klassis.

Sotsiaalsed vabamõtlejad üritasid hüpata Einsteini reele, üritades tema teoorias näha nende endi moraalse ja kultuurilise relativismi peegeldust. Kuidas võis keegi veel otsida absoluutseid väärtusi moraalis, kommetes või poliitikas, kui isegi füüsika täppisilmas polnud neile enam ruumi? Einstein pareeris: teda on võõriti mõistetud. Relatiivsusteooria polnud hüljanud absoluutset tõtt, vaid üksnes aja ja ruumi võltsabsoluute. Võtnud omaks Minkowski neljamõõtmelised invariandid, tegi Einstein koguni abitu katse muuta oma teooria nimetus invariantide teooriaks (sks. Invariantstheorie).

Oma erialal jäi Einstein üksiklaseks, eemale peavoolustest. Parimad füüsikud kodunesid relativistlikes arvutustes, vähemasti erirelatiivsusteoorias, imetledes selle ilu. Kuulus ja austatud Einstein aga ei üritanud eales võtta endale füüsikute kogukonna juhi osa.

Osaliselt oli see üksildus seotud ka Einsteini ametikäiguga, mis viis teda harva või üldse mitte kokku õpilastega. Teiseks tõkkeks olid tema tööharjumused, miä takistasid nooremaid kolleege tema stiili omaks võtmast. Osalt olid süüdi ka teooriad ise. Erirelatiivsusteooria sai täielikult valmis mõne aastaga pärast 1905ndat. Polnud vaja suurt koolkonda ennustusi lihvima ega eksperimentaatorite jõuke neid järele proovima. Üldrelatiivsusteooriaga oli lugu veelgi kehvem, sest alles pärast tema surma sai see katsega laiemalt hõlmatavaks.

Eelkõige isoleeris Einsteini tema enda maailmavaade, mis ujus vastu toonaseid vaimseid vooluseid. Albert Einstein oli kompromissitu ratsionalist, kel oli sügav usk, et Universum rajaneb loogilisel alusel. Seda usku personifitseeris ta tihti Jumala või Vana Enda nimega, olgugi et ta vankumatult keeldus mistahes religiooni kombeid täitmast.

Nooruses mõjustas Einsteini tugevasti positivistlik füüsikust filosoof Ernst Mach, kes sisendas, et füüsikas peab tugevasti juurduma vaatlusprotsessi kriitiline läbivaatus. See oli ilmseks teeviidaks relatiivsusteooria arendamisel. Küpsedes hakkas Einstein suhtuma puhtempiirilisse teadusse kui "Machi väiksesse ratsusse", olesesse, "kes võib küll kitkuda kahjulikke umbrohte", kuid "kes ei suuda sünnitada midagi elavat". Siit ilmneb, et Einsteini vaim oli Galilei omast platonistlikumgi.

Einsteini Universumis ei olnud kohta meelevaldsustele. Inimmõistuse võimel selgitada, miks maailm on just selline, nagu ta on, ei pidanud olema mingeid piire. Niels Bohr ja tema jüngrid, kelle tööd peagi vaatluse alla võtame, lükkasid selle vaate kategooriliselt tagasi. Nemad väitsid end näidanud olevat, et inimmõistuse võimel loodust täielikult hoomata on piirid.

Kuigi ta jäi üksi, klammerdus Einstein visalt oma seisukohtade külge. Oma hilisaastail võttis ta oma lähenemisviisi loodusele kokku ainsas fraasis: "Tõeliselt huvitab mind vaid üks asi: kas Jumalal oli maailma luues üldse midagi valida."

Üldrelatiivsusteooria kasvab välja erirelatiivsusteooriast, lisades sellele ekvivalentsuse printsiibi, mis vormistab seose gravitatsiooni ja kiirenevate taustsüsteemide vahel. See viib sellisele mehaanika ümberkujundamisele, milles gravitatsiooni seletab kõvera aegruumi geomeetria, ilma et oleks tarvis mingit jõudu. Siit lähtub omakorda aja sõltuvus kõrgusest gravitatsioonivälja tekitava keha kohal. See teooria ennustab ka valguskiire kallet Päikese gravitatsiooniväljas, mis on kaks korda suurem kui Newtoni gravitatsiooniteooria järgi arvutatu. Kalde mõõtmine päikesevarjutuse ajal andis Einsteini teooriaga ühtiva tulemuse ja tegi temast kuulsa mehe. Teooriast järeldub ühtlasi, et Universum ei saa olla staatiline. Seda kinnitasid järgnenud vaatlused. Järelduvad ka aegruumi äärmuslikud moonded, mida praegu tuntakse mustade aukudena. Kuigi üldrelatiivsusteooria on aluseks nüüdsele kosmoloogiale, jääb ta ebatäielikuks, kuni teisi jõude peale gravitatsiooni pole suudetud viia geomeetria alla.