Eelmises osas kirjeldasime tööd, mida teeb elektriväli laengute liigutamisel. 9. klassist tuttav mõiste pinge on otseselt seotud elektrivälja poolt tehtud tööga.
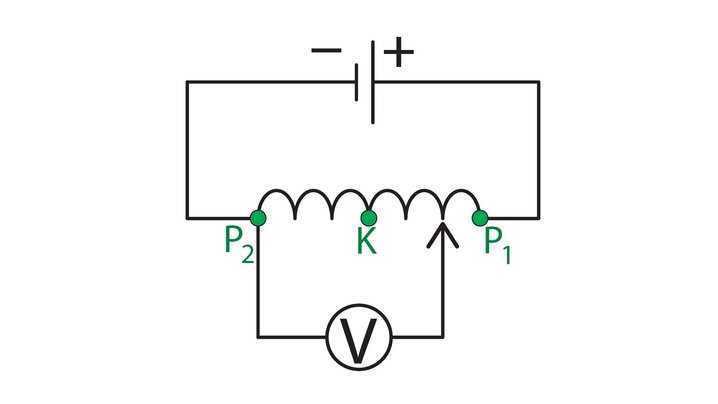
Joonisel 1.22 on kujutatud vooluringi ühendatud reostaadi mähist. Pinget reostaadil saab mõõta voltmeetriga, mille üks klemm on ühendatud püsivalt reostaadi mähise ühe otsaga ja mille teist klemmi saame nihutada reostaadi mähise keerdudel.
Kõige suurem on pinge väärtus reostaadi mähise otstel, st punktide ja vahel. Kui nihutame liugkontakti punktist punkti K suunas, siis pinge väärtus väheneb.
Kui mõtleme tööst, mida elektriväli teeb laengute liigutamisel, siis ilmselt on see suurim, kui laengud liiguvad läbi terve reostaadi. Seda mõttekäiku saab üldistada ja öelda, et suurema pingega töötavad seadmed teevad rohkem tööd – nii on vaja röntgenlambis elektronide kiirendamiseks vähemalt , et toota suure energiaga röntgenkiirgust, aga LED-lambi põlemiseks piisab pingest .
Pinge mistahes kahe punkti vahel on arvuliselt võrdne tööga, mida tehakse ühekulonilise laengu nihutamisel ühest punktist teise. Pinge definitsioonvalem on
Vooluringis mõõdetakse pinget mistahes kahe punkti vahel voltmeetriga.
Võrgupinged maailma riikides jäävad vahemikku –230V. Kõige madalam on pinge Jaapanis: , Eestis ja Euroopas on pinge vooluvõrgu klemmidel keskmiselt 230V, Ameerika Ühendriikides . Kui osta seadmeid välismaalt, tuleb uurida seadme tehnilisi andmeid, sealhulgas ka nimipinget.
Elektrivälja kirjeldamiseks kasutatakse ka elektrivälja potentsiaali mõistet.
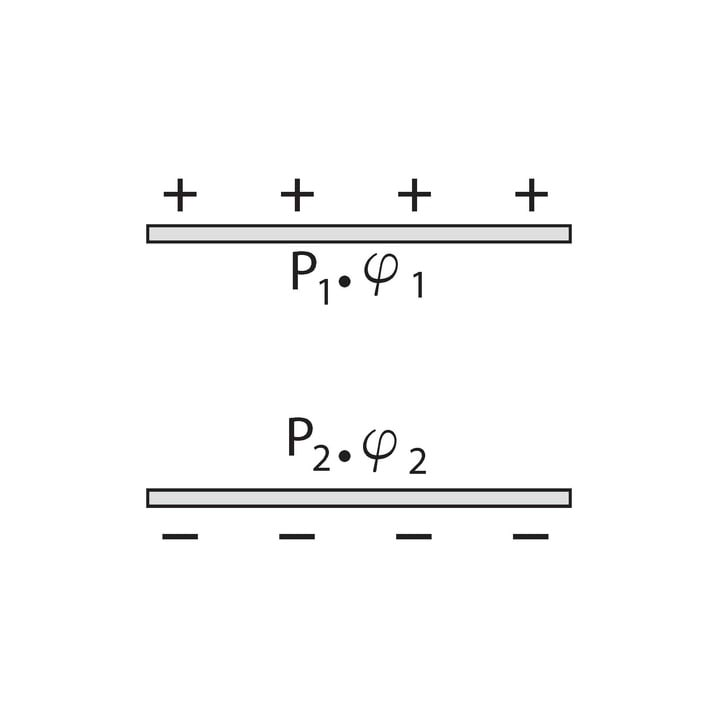
Joonisel 1.23 oleme laetud plaatide tekitatud elektriväljas märkinud punktid ja . Neid punkte iseloomustab ka elektrivälja potentsiaal, mille tähistame kreeka tähega (fii). Elektrivälja potentsiaal on seotud elektrivälja asetatud laengu potentsiaalse energiaga antud punktides. Kuna punktis on laengu potentsiaalne energia suurem kui punktis , saame sama öelda ka elektrivälja potentsiaali kohta: .
Elektrivälja potentsiaal näitab, kui suur on elektrivälja potentsiaalne energia mingis punktis positiivse ühiklaengu kohta.
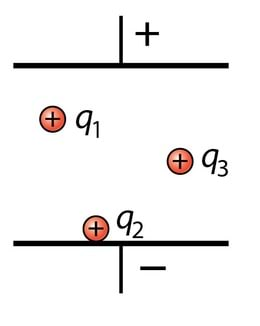
Miks just ühiklaengu kohta? Aga sellepärast, et elektrivälja potentsiaal on välja omadus, see ei sõltu sellest, kui suur laeng seal väljas paikneb. Nii mitu korda, kui erinevad kehade laengud, erinevad ka laetud kehade potentsiaalsed energiad antud elektrivälja punktis.
Elektrivälja potentsiaal on väljendatav valemiga:
Rõhutame, et elektrivälja potentsiaal iseloomustab elektrivälja sõltumata sellest, kas seal on laetud keha või mitte.
Füüsikas on suurema tähendusega elektrivälja kahe punkti potentsiaalide erinevus, sest see määrab ära, kui palju teeb elektriväli tööd laengu nihutamisel elektrivälja ühest punktist teise.
Kui mõõdame pinget elektriseadme kahe punkti vahel, siis mõõdame nende punktide potentsiaalide erinevust . Pinge ja elektrivälja potentsiaali vahelist seost väljendab valem
Näiteks kui mõõdame vooluringis vooluallika klemmipingeks , saame öelda, et klemmide potentsiaalide erinevus on 9V.
Nii pinge kui ka elektrivälja potentsiaali ühikuks on 1V.
Pinget ja potentsiaali ei tohi omavahel segamini ajada. Erinevus nende kahe füüsikalise suuruse vahel:
- pinge võrdleb kahe punkti potentsiaali ja annab võimaluse arvutada näiteks elektrivälja poolt tehtavat tööd laengute nihutamisel ühest punktist teise, potentsiaal aga kirjeldab olukorda ühes punktis;
- pinget mõõdetakse voltmeetriga otseselt, potentsiaali kaudselt. Kasutusele on võetud ka erinevad tähised: pinge tähis on ja elektrivälja potentsiaali tähis on (fii).
Enamik traditsioonilisi tähiseid on eesti keelde tulnud saksa kultuuriruumist ja sageli vene keele kaudu, mistõttu eestikeelsed füüsikaliste suuruste tähistused erinevad ingliskeelses erialakirjanduses kasutatavatest tähistustest. Inglise keeles on võetud tähiseks vastava sõna esimene täht. Näiteks tiheduse tähis on meil , aga inglise keeles (density), meil on töö tähis , inglise keeles (work), meil on pinge tähis , inglise keeles (voltage). Samuti tähistatakse inglise keeles -tähega elektrilist potentsiaali. Nii võime leida ingliskeelsetes õpikutes üleskirjutuse , mis näitab, et pinge on võrdne potentsiaalide vahega klemmide otstel ja selle väärtus on volti.
Uurime elektrivälja potentsiaali kahe sirge traatelektroodi vahel, mis on asetatud ammoniaagi vesilahusega immutatud paberile ja ühendatud alalisvooluallikaga pingeväärtusega . (Vt joonis 1.24.)
Potentsiaalide mõõtmiseks kasutame voltmeetrit, mille üks klemm on ühendatud negatiivse elektroodiga. Sellel elektroodil on potentsiaal vähima väärtusega ja potentsiaali nullnivoo on kokkuleppeline, loeme selle võrdseks nulliga . Voltmeetri teise klemmi saame ühendada mistahes välja punktiga. Kasutame valemit . Kui
asendame , saame öelda, et voltmeetri näit on ühtlasi ka antud punkti potentsiaali väärtus:
Katses uurime elektrivälja potentsiaale kuues erinevas punktis. Kui ühendada liikuv klemm punktiga (joonis 1.24a), näitab voltmeeter . Sama potentsiaali väärtuse saame ka siis, kui ühendame liikuva klemmi punktiga . Nende kahe punkti potentsiaalide erinevus on seega . Meie mõõtmised ja arvutused näitavad, et pinge elektroodi ja punkti vahel on , aga pinge punkti ja vahel on .
| Elektrivälja punkt | Elektrivälja punkti potentsiaal |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
Kui mõõta sarnaselt kõikide teiste punktide potentsiaalid (vt tabel 1.2) ja arvutada potentsiaalide erinevused, märkame, et
a) punktide ja vahel ning ka punktide ja vahel on pinge ;
b) pinge punktide ja vahel on , samuti punktide ja ning ja vahel;
c) punktide ja ning ja vahel on pinge ;
d) suurim on pinge kahe elektroodi vahel, kus .
Elektriväli teeb tööd ainult siis, kui on olemas potentsiaalide erinevus (pinge). Mida suurem on elektrivälja punktide potentsiaalide erinevus, seda suurem on pinge ja elektrivälja töö. Kui ehk potentsiaalide erinevus puudub, siis ei tehta ka tööd.
Valemina saab selle kirja panna kas
või
Potentsiaali mõiste on kesksel kohal näiteks närvirakkude toimemehhanismi seletamisel
bioloogias ja vooluallika parameetrite väljaarvutamisel elektrokeemias.
Mikromaailma füüsikas kasutatakse energiaühikut elektronvolt (). Kuidas on see seotud energia põhiühikuga 1J? Loogiline oleks arvata, et kui on tegu üliväikeste osakestega, näiteks elektronide, prootonite või footonitega, siis on ka nende energia võrreldes makromaailma objektidega väga väike. Nii ta ongi, sest . Milline osake omab energiat ? Sellises suurusjärgus on nähtava valguse footoni energia. Tuumaosakeste energiat mõõdame megaelektronvoltides (). Näiteks et eraldada raua aatomi tuumast üks tuumaosake, tuleb kulutada energiat u .
Ühik on tuletatud meile tuttavast valemist . Kui kasutame elektrilaengu ühikut ja pinge ühikut 1V, on nii töö kui ka energia ühik 1J. Kui kasutame ühe kuloni asemel elementaarlaengut , ongi töö ja energia ühikuks , mis on väga sobilik mikromaailma energia ja töö ühikuks.
on võrdne tööga, mida teeb elektriväli elektroni viimisel ühest väljapunktist teise, kui nende punktide potentsiaalide erinevus on 1V. Makromaailmas on see suurus üliväike.