Et määrata tähistaeva objekte täpsemalt, on vaja taevasfääril defineerida koordinaadid.

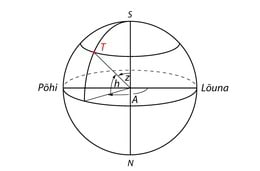
Horisondilised koordinaadid on intuitiivselt lihtsad – üks koordinaat sarnaneb oma olemuselt tavalise geograafilise asimuudiga ja teine on kõrgus horisondist  (joonis 11). Siin kasutatakse juba meile tuttavaid mõisteid seniit, nadiir ja horisont. Kõike seda on loomulikult võimalik ka matemaatiliselt rangelt määratleda, seda me siin aga ei tee. 

Niisiis on asimuut $A$ nurk lõuna- (mõnikord siiski ka põhja) suuna vahel horisondi tasandis, kõrgus $h$ on nurk tähele mineva vaatesuuna ja horisondi vahel ning horisondilised koordinaadid on $(A,h)$. Astronoomias loetakse asimuudi nurka enamasti lõunasuunast ning päripäeva (kellaosuti liikumise) suunas. Näiteks lõunasuuna asimuut on $0^{\circ }$, läänesuuna asimuut on ${90}^{\circ }$. Horisondi kõrgus on $0^{\circ }$, seniidi kõrgus on $+{90}^{\circ }$. Kui objektid on allpool horisonti, siis on nende kõrgus negatiivne.

Siiski esineb ka sellised käsitlusi (ja arvutiprogramme), kus horisondiliste koordinaatide asimuuti loetakse põhjasuunast ja päripäeva, nii et igaks juhuks tuleb alati vaadata definitsioone.  

Öö jooksul tõusevad tähed ida poolt, jõuavad suurima kõrguseni ning laskuvad (loojuvad) ligikaudu läände. Suurima ja vähima kõrguseni jõudmist nimetatakse kulminatsiooniks või täpsemalt ülemiseks ja alumiseks kulminatsiooniks. Nende tähtede puhul, mis antud laiuskraadil ei looju, näemegi nii ülemist kui alumist kulminatsiooni.

Niimoodi defineeritud koordinaatide väärtused aga muutuvad pidevalt ning lisaks sellele on need ka lokaalsed, st sõltuvad vaatleja asukohast (erinevas asukohas vaatlejal on ju erinev horisont).

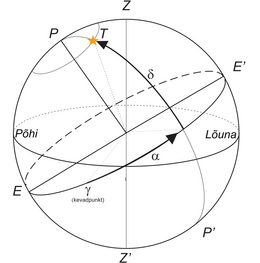
Ekvaatorilised koordinaadid. Kui tahame konstrueerida koordinaate, mis oleksid sõltumatud tähistaeva pöörlemisest ja vaatleja asukohast, siis tuleb koordinaadid siduda üldise tähistaeva pöörlemisega. Lähtume taevaekvaatori diagonaaljoonest $EE\text{'}$ ja sellele vastavast taevaekvaatori tasandist (joonis 12). Üks sobiv koordinaat on tähe nurkkaugus taevaekvaatori tasandist pooluse $P$ suunas: kääne $\delta$. Võrreldes Maa geograafiliste koordinaatide süsteemiga sarnaneb see laiuskraadile. Seega omab taevaekvaator käänet $0^{\circ }$, taeva põhjapoolus käänet $+{90}^{\circ }$ ja lõunapoolus käänet $-{90}^{\circ }$ . Teine koordinaat peab olema nurk piki taevaekvaatorit. Ehkki matemaatiliselt võttes on ükskõik, milline punkt taevasfääril piki ekvaatorit fikseerida nullpunktiks, on selleks punktiks siiski valitud nn kevadpunkt või pikemalt kevadise võrdpäevsuse punkt ${\rm Y}$ – suund, kus ekliptika (vt p. 1.4.1) lõikub taevaekvaatoriga ehk lihtsamalt Päikese asukoht kevadisel pööripäeval. Teiseks koordinaadiks, otsetõusuks $\alpha$, nimetatakse nurka selle kevadpunkti ning taevaekvaatorile projekteeritud tähesuuna vahel*. Otsetõus kasvab vastupäeva. Otsetõusu koordinaat sarnaneb geograafiliste koordinaatide pikkuskraadiga, mille puhul nullpunkt on Greenwitchi meridiaalil (vt joonis 13). Ekvaatorilised koordinaadid on seega $(\alpha ,\delta )$.

Otsetõusu koordinaatide väärtuseid väljendatakse astronoomias sageli nn ajamõõdus. Lähtekohaks on see, et ööpäevaga pöörleb tähistaevas täispöörde võrra 24 tunniga. Seega ${360}^{\circ }$ vastab 24 tunnile (kirjutatakse ${24}^h$) ehk $1^h={15}^{\circ }$. Sarnaselt saame, et $1^m={15}^{\prime }$ ja $1^s={15}^{\prime \prime }$, kus "m" ja "s" tähistavad vastavalt ajalist minutit ja sekundit. Näiteks heleda tähe Veega ekvaatorilised koordinaadid on $(\alpha ,\delta )=({18}^h{37}^m,+{38}^{\circ }{47}^{\prime })$. Arvutage, milline on otsetõusu koordinaat tavalistes nurgaühikutes.

Need koordinaadid tähistaeva ööpäevasel pöörlemisel ei muutu (niivõrd kuivõrd Maa pöörlemise telg ei muutu) ja on sõltumatud vaatleja asukohast.

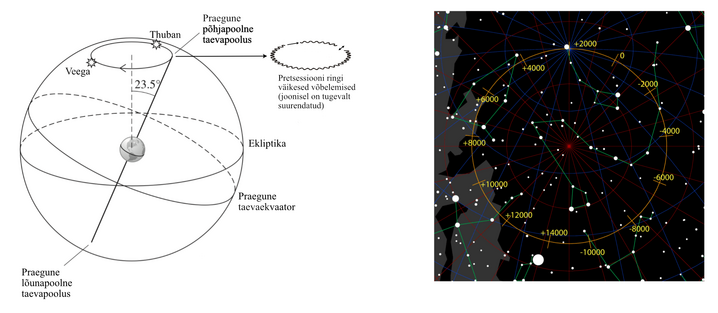
Kuid siiski, Maa ei ole ideaalselt kerakujuline, vaid on pisut lapik. See asjaolu ning Kuu, Päikese ja Jupiteri poolt mõjuvad gravitatsioonijõud tingivad Maa pöörlemistelje ja sellega seotud pooluse asukoha aeglase muutumise (güroskoobi efektist tingitud pretsessioon – meenutage füüsikakursuse vastavaid valemeid). Selle tulemusena kirjeldab pooluse asend taevasfääril umbes  $26000$ aasta jooksul ringi raadiusega umbes $23,5^{\circ }$ – see on nurk Maa pöörlemistelje ja Maa orbiidi tasandi normaali vahel (joonis 14). Ka kevadpunkti asukoht ekliptikal muutub aeglaselt, nihkudes lääne suunas kiirusega umbes ${50}^{\prime \prime }$ aastas. Seetõttu on praegu kevadpunkt Kalade tähtkujus, ehkki seda tähistatakse antiikastronoomia tavade kohasel Jäära tähtkuju märgiga ${\rm Y}$. Pooluse ja kevadpunkti liikumise tõttu muutuvad ka tähtede koordinaadid (koordinaatide nullpunktid muutuvad), mistõttu on tihti vaja täpsustada, millise aja koordinaatidega on tegemist.