Olete kindlasti märganud, et prilliklaasid ei ole tasapinnalised, vaid kumerad ning erinevatest kohtades erineva paksusega. Vaadates esemeid läbi prillide, paistavad nad meile teistsuguse suurusega, kui nad tegelikult on. Miks see nii on?

Kuna prilliklaaside pind on kumer, siis sealt läbi läinud valgus muudab murdudes oma suunda. Prilliklaasid on konstrueeritud nii, et neid läbiv paralleelne valgusvihk muutub koonduvaks või hajuvaks valgusvihuks. Füüsikas nimetatakse selliseid kehasid läätsedeks.

Läätsede pinnad on tehtud sfäärikujulised. Nende sfääride kõverusraadiused määravad ka läätse omadused. Läätsed võivad olla kas kumerläätsed või nõgusläätsed.

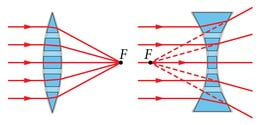
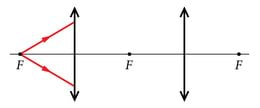
Kumer- ja nõgusläätse omadusi on kõige lihtsam seletada, kui kujutame neid koosnevana lõigatud tippudega prismadest ning ühest klaasplaadist keskel, mis ligikaudselt jäljendavad läätse kuju (vt joonist). Sellisel juhul – näiteks kumerläätse puhul – ülemistele prismadele langenud kiired murduvad allapoole, keskmist klaastahvlit läbivad kiired ei murdu ning alumist klaasprismat läbinud kiired murduvad ülespoole. Sealjuures on klaasprismad valitud sellised, et kõik paralleelse kiirtekimbu kiired koonduvad punktis F. Nõguspeegli korral saab arutleda analoogiliselt.

Läätsede kirjeldamiseks on vaja teada olulisi läätsi iseloomustavaid mõisteid.

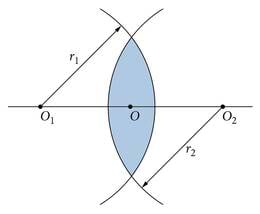
• Läätse optiliseks peateljeks nimetatakse läätse pindasid moodustavate sfääride keskpunkte ühendavat sirget (vt joonist lehekülje keskel).
• Läätse optiliseks keskpunktiks O nimetatakse läätse keskel optilisel peateljel asetsevat punkti.
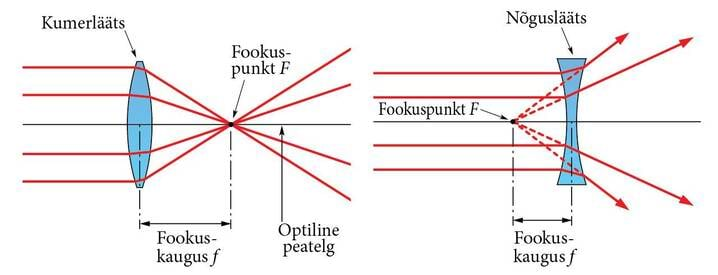
• Kumerläätse fookuseks F nimetatakse punkti, kus koondub läätsele langev paralleelne valgusvihk.
• Fookuskauguseks nimetatakse fookuse F ja optilise keskpunkti O vahelist kaugust. Fookuskaugust tähistatakse tähega f. Nõgusläätse korral nimetatakse läätse fookuseks punkti, kus koonduvad läätse läbinud hajunud kiirte pikendused. Kuna hajunud kiirte pikendused koonduvad teisel pool läätse, on nõgusläätse fookuskaugus kokkuleppeliselt miinusmärgiga.
• Läätse optiliseks tugevuseks (D) nimetatakse läätse fookuskauguse pöördväärtust:

Seega

Läätse optilise tugevuse mõõtühikuks on dioptria (lühend dpt). Üks dioptria on sellise läätse optiline tugevus, mille fookuskaugus on 1 meeter: 1 dpt = 1/1 m. Läätse optilise tugevuse määramiseks tuleb mõõta läätse fookuskaugus meetrites ning arvutada selle pöördväärtus

Kumerläätse fookuskauguse määramiseks tuleb leida koht, kus läätsele langenud paralleelne valgusvihk muutub punktiks. Paralleelse valgusvihu tekitab näiteks päike – lääts tuleb asetada risti päikesekiirtega ning viia pinnast sellisele kaugusele, kus lääts tekitab pinnale valgustäpi. Läätse ja pinna vaheline kaugus ongi sellisel juhul kumerläätse fookuskaugus.

Tavaliselt kasutatakse optilistes seadmetes mitut läätse korraga. Kahest või mitmest lähestikku asetsevast läätsest koosnevat optilist süsteemi nimetatakse liitläätsedeks. Liitläätse optiline tugevus on võrdne üksikute läätsede optiliste tugevuste summaga:

Näiteks kui liitlääts koosneb kahest kumerläätsest, mille optilised tugevused on vastavalt 2 dpt ja 3 dpt, siis nendest läätsedest koosneva liitläätse optiline tugevus on 5 dpt.