Mõõtmine

Füüsiku pilguga

Kui maavärin tabab asustatud piirkonda, võib ta maju purustada või ümber paisata. Kuid mõnel pool paneb maavärin maju poolenisti maasse vajuma, otsekui seisaksid need püdela vedeliku, mitte kindla maa peal. Kuidas saab maja maasse vajuda? Vastus on selles peatükis.

Teadus ja tehnika põhinevad mõõtmistel ja võrdlustel. Niisiis on meil tarvis reegleid, kuidas asju mõõta ja võrrelda, ning katseid, et panna paika nende mõõtmiste ja võrdluste ühikud. Üks füüsika (ja tehnika) eesmärke on nende katsete kavandamine ja läbiviimine.

Näiteks püüavad füüsikud luua erakordselt täpseid kelli, et iga ajahetke või ajavahemikku täpselt mõõta ja võrrelda. Võib küsida, kas säärast täpsust on tegelikult vaja või kas on ta üldse vaeva väärt. Toome ühe näite: ilma erakordselt täpsete kelladeta poleks olnud võimalik luua globaalset positsioneerimissüsteemi (GPS), mis tänapäeval on ülemaailmses mere- ja lennunavigatsioonis hädavajalik.

NB Selles peatükis kirjeldatakse SI ühikute põhiühikute definitsioone, mis kehtisid kuni 2019. aastani. Õpiku seda peatükki on kavas uuendada.

Asjade mõõtmine

Me avastame füüsikat, õppides tundma sellega seotud suurusi. Füüsikalised suurused on näiteks pikkus, aeg, mass, temperatuur, rõhk ja elektrivoolu tugevus.

Iga füüsikalist suurust mõõdetakse omaette ühikutes, võrreldes teda tema etaloniga. Ühik on nimi, mille me teatud mõõtu suurusele anname – näiteks meeter (m) on pikkuse ühik. Etalon vastab täpselt suuruse ühele ühikule. Nagu varsti näeme, on täpselt 1 meetrile vastava pikkuse etaloniks kaugus, mille valgus läbib vaakumis sekundi teatud kindla murdosa jooksul. Me võime ühikut ja tema etaloni defineerida meelevaldselt, ent on oluline teha seda nõnda, et terve maailma teadlased peaksid meie definitsioone nii mõistlikuks kui ka praktiliseks.

Kui oleme sisse seadnud näiteks pikkuse etaloni, peame me välja töötama protseduurid, mille abil saab suvalist pikkust, olgu selleks vesiniku aatomi raadius, rularatta läbimõõt või kaugus täheni, väljendada etaloni kaudu. Ligikaudu pikkusetalonile vastava joonlauaga mõõtmine on üks võimalikke sääraseid protseduure. Ent paljud võrdlused, mida me teeme, on paratamatult kaudsed. Joonlauda kui sellist ei saa kasutada aatomi raadiuse või tähe kauguse mõõtmiseks.

Füüsikalisi suurusi on nõnda palju, et nende korrastamine on omaette probleem. Õnneks pole nad kõik sõltumatud, näiteks kiirus on pikkuse ja aja suhe. Nõnda me valime välja – rahvusvahelise kokkuleppega – väikese arvu füüsikalisi suurusi, nagu on pikkus ja aeg, ning määrame etalonid ainult neile. Siis defineerime kõik muud füüsikalised suurused valitud baassuuruste ja nende etalonide kaudu. Näiteks kiirust defineeritakse baassuuruste pikkuse ja aja ning nende etalonide kaudu.

Etalonid peavad olema nii kättesaadavad kui ka muutumatud. Kui me defineerime pikkuse etaloni väljasirutatud käe nimetissõrme ja ninaotsa vahelise kaugusena, on meie etalon kahtlemata kättesaadav – kuid mõistagi pole see kõigil inimestel ühesugune. Teaduse ja tehnika täpsusetaotlus sunnib kõigepealt nõudma etalonide muutumatust. Seejärel nähakse suurt vaeva kättesaadavusega, tehes etalonidest kasutajatele vajalikud koopiad.

Rahvusvaheline mõõtühikute süsteem

1971. aastal valis XIV kaalude ja mõõtude peakonverents seitse suurust baassuurusteks ja moodustas neist aluse rahvusvahelisele mõõtühikute süsteemile, mida selle prantsuskeelse lühendi järgi nimetatakse SI-ks ja mis kõnekeeles on tuntud ka kui meetermõõdustik. Tabelis 1-1 on esitatud kolme baassuuruse – pikkuse, massi ja aja – ühikud, mida me käesoleva raamatu esimestes peatükkides kasutame. Need ühikud defineeriti „inimliku mõõdupuu” järgi.

TABEL 1-1 SI kolme baassuuruse ühikud

Suurus	Ühiku nimi	Ühiku tähis
Pikkus	meeter	$m$
Aeg	sekund	s
Mass	kilogramm	s

Paljud SI tuletatud ühikud on defineeritud nende baasühikute kaudu. Näiteks SI võimsusühik nimega vatt (W) on defineeritud massi, pikkuse ja aja ühikute kaudu. Nagu näete 7. peatükis,

(1-1)

1 v a t t = 1 W = 1 k g \cdot \frac{m^{2}}{s^{3}}

kus ühikuid viimases võrduses loetakse kilogramm korda ruutmeeter sekundi kuubi kohta.
Et esitada füüsikas sageli ette tulevaid suuruste väga väikesi ja väga suuri väärtusi, kasutame arvude standardkuju 10 astmete kaudu. Selles tähistuses

(1-2)

3560000000 m = 3, 56 \times 10^{9} m

ja

(1-3)

0, 000000492 s = 4, 92 \times 10^{- 7} s

Arvutites on arvu standardkuju mõnikord veelgi lakoonilisem, nagu 3,56 E9 ja 4,92 E-7, kus E tähendab „kümne astet (eksponenti)”. Mõnedes kalkulaatorites, kus E-d asendab tühik, on see lakoonilisemgi.
Kui tegemist tuleb mõõtmistulemuste väga suurte või väga väikeste väärtustega, kasutame mugavuse mõttes eesliiteid, mis on kirjas tabelis 1-2. Nagu näete, tähendab iga eesliide arvu 10 teatud astet, mida kasutatakse tegurina. SI ühikule eesliite lisamine tähendab, et ühik korrutatakse vastava teguriga läbi. Nõnda võime teatud võimsuse kirja panna kui

(1-4)

1, 27 \times 10^{9} v a t t i = 1, 27 g i g a v a t t i = 1, 27 G W

või teatud ajaintervalli kui

(1-5)

2, 35 \times 10^{- 9} s = 2, 35 n a n o s e k u n d i t = 2, 35 n s

Mõned eesliited, näiteks ühikutes milliliiter, sentimeeter, kilogramm ja megabait, on teile küllap tuttavad.

SI ühikute eesliited

Ühikute teisendamine

Tihti on vaja ühikuid, milles füüsikalised suurused on esitatud, muuta. Me teeme seda ahelmeetodi abil, korrutades algse mõõtmistulemuse väärtuse teisendusteguriga (ühikute jagatisega, mis on võrdne ühega). Kuna näiteks $1 m i n$ ja $60 s$ on võrdsed ajavahemikud, on meil

\frac{1 m i n}{60 s} = 1

ja

\frac{60 s}{1 m i n} = 1

Niisiis saab jagatisi $(1 m i n) / (60 s)$ ja $(60 s) / (1 m i n)$ kasutada teisendusteguritena. See pole sama, kui kirjutada $1 / 60 = 1$ või $60 = 1$ ; mõõtmise iga arvväärtust ja tema ühikut tuleb vaadelda koos. Et mingi suuruse korrutamine ühega jätab suuruse samaks, võime me teisendustegurid sisse tuua iga kord, kui neid vajame. Ahelteisenduses kasutame tegureid, et vabaneda soovimatutest ühikutest. Näiteks et $2 m i n$ teisendada sekunditesse, peame korrutama

(1-6)

2 m i n = (2 m i n) (1) = (2 m i n) (\frac{60 s}{1 m i n}) = 120 s

Kui soovimatud ühikud ei taandu teisendusteguriga välja, võib proovida tema pöördväärtust. Teisendustes alluvad ühikud samadele algebrareeglitele nagu muutujad ja arvud. Lisas D on toodud teisendustegurid SI ja teiste mõõtühikute süsteemide vahel, kaasa arvatud SI-välised ühikud, mida Ameerika Ühendriikides siiani kasutatakse. Kuid teisendustegurid on seal kirjutatud laadis $1 m i n = 60 s$ , mitte suhtena. Järgmine näidisülesanne näitab, kuidas sääraseid suhteid kokku panna.

Legendi järgi jooksis Pheidippides 490. aastal eKr Marathonist Ateenasse viima sõna kreeklaste võidust pärslaste üle ning tema kiirus oli seejuures tõenäoliselt

23

hippikoni tunnis (

23 h i p p i k o n i / h

). Hippikon on Vana-Kreeka pikkusühik, nagu ka staadion ja plethron:

1 h i p p i k o n

oli

4 s t a a d i o n i t

,

1 s t a a d i o n

6 p l e t h r o n i t

; praegusaegsetes ühikutes on

1 p l e t h r o n

30, 8 m

. Kui kiiresti jooksis Pheidippides kilomeetrites sekundis (

k m / s

)?

Lahendus

JUHTMÕTE Ahelteisendustes kirjutame teisendustegurid suhetena, mis lubavad välja taandada soovimatud ühikud.

Arvutused: Meil on

23 h i p p i k o n i / h = (23 \frac{h i p p i k o n i}{h}) (\frac{4 s t a a d i o n i t}{1 h i p p i k o n}) (\frac{6 p l e t h r a t}{1 s t a a d i o n}) \times (\frac{30, 8 m}{1 p l e t h r o n}) (\frac{1 k m}{1000 m}) (\frac{1 h}{3600 s}) = 4, 7227 \times 10^{- 3} k m / s \approx 4, 7 \times 10^{- 3} k m / s - ---------------- - - ---------------- -

Heeringatünder on Inglise mahuühik äsja püütud heeringate jaoks:

1 t ¨ u nder = 170, 474

liitrit} (

l

) kala, s.o umbes 750 heeringat. Oletame, et Saudi-Araabias tuleb

1255

tündrist koosnev last tollis klaarimiseks deklareerida kuupkovidotes, kus kovido on araabia pikkusühik (araabia küünar):

1 k o v i d o = 48, 26 c m

. Mitu kuupkovidot see teeb?

Lahendus

JUHTMÕTE Lisast D näeme, et $1 l$ on sama mis $1000 c m^{3}$ . Et teisendada kuupsentimeetrid kuupkovidoteks, peame sentimeetrite ja kovidote vahelise teisendusteguri kuupi tõstma.

Arvutused: Paneme kirja järgmise ahelteisenduse:
$1255 t ¨ u ndrit$

= (1255 l i i t r i t) (\frac{1704741}{1 t ¨ u nder}) (\frac{1000 c m^{3}}{11}) {(\frac{1 k o v i d o}{48, 26 c m})}^{3} = 1, 903 \times 10^{3} k o v i d o - ------------------- - - ------------------- -

Ülesannete lahendamise juhised

Tähendusega numbrid ja kümnendkohad. Kui su kalkulaator näidisülesande 1-1 arvutatud vastust automaatselt ei ümardanud, võis näidikule ilmuda $4, 72266666667 \times 10^{- 3}$ . Enamikul neist kümnendkohtadest pole mõtet. Me ümardasime vastuse $4, 7 \times 10^{‑ 3} k m / s$ , et mitte jätta muljet, et see on täpsem kui algandmed. Antud kiiruse $23 h i p p i k o n i / h$ arvväärtuses on kaks numbrit, mida nimetatakse tüvenumbriteks. Me ümardasime vastuse kahe tüvenumbrini. Käesolevas raamatus ümardatakse arvutuste lõpptulemused tihti kõige väiksema tüvenumbrite arvuni, mis on lähteandmetes. (Mõnikord esitatakse siiski veel üks tüvenumber.) Kui viimane ärajäetav number on $5$ või suurem, ümardatakse viimane allesjääv number ülespoole, muul juhul jäetakse ta muutmata. Näiteks $11, 3516$ ümardatakse kolme tüvenumbrini kui $11, 4$ ja $11, 3279$ ümardatakse kolme tüvenumbrini kui $11, 3$ . (Näidisülesannete vastused käesolevas raamatus on tavaliselt antud sümboliga $=$ , mitte $\approx$ , isegi kui vastus on ümardatud.)

Kui ülesandes on antud näiteks arv $3, 15$ või $3, 15 \times 10^{3}$ , on tüvenumbrite arv silmanähtav, aga kuidas on arvuga $3000$ ? Kas see on teada ainult ühe tüvenumbrini ( $3 \times 10^{3}$ )? Või on see teada koguni nelja tüvenumbrini ( $3, 000 \times 10^{3}$ )? Käesolevas raamatus me eeldame, et kõik nullid lähteandmete arvudes nagu $3000$ on tüvenumbrid, kuid muudes raamatutes võib olla teistsuguseid kokkuleppeid.

Ärge ajage tüvenumbreid segamini kümnendkohtadega. Pikkustel $35, 6 m m$ , $3, 56 m$ ja $0, 00456 m$ on kõigil kolm tüvenumbrit, kuid vastavalt üks, kaks ja viis kümnendkohta.

Pikkus

1792. aastal seadis äsja sündinud Prantsuse Vabariik sisse uue kaalude ja mõõtude süsteemi. Selle nurgakivi oli meeter, mida defineeriti kui üks kümnemiljondik põhjapooluse ja ekvaatori vahemaast. Hiljem loobuti sellest Maaga seotud etalonist praktilistel põhjustel ja meeter määratleti kaugusena kahe peene kriipsu vahel, mis on graveeritud plaatina-iriidiumisulamist varva – meetrietaloni – otste lähedale. Meetrietaloni säilitatakse Rahvusvahelises Mõõtude ja Kaalude Büroos Pariisi lähedal. Etaloni täpsed koopiad saadeti etalonilaboritele üle maailma. Neid sekundaaretalone kasutati teiste, lihtsamini kättesaadavate tugi- ja tööetalonide valmistamiseks, nii et viimaks oli iga mõõdupuu usaldusväärsus tagatud meetrietalonist lähtuva keeruka võrdluste ahela abil.

Aja jooksul tekkis tarvidus täpsema etaloni järele kui kaks peent kriipsu metallvardal. 1960. a võeti kasutusele valguse lainepikkusel põhinev uus meetri definitsioon. Täpsemalt, meetrit defineeriti kui $1650763, 73$ lainepikkust oranžikaspunases valguses, mida kiirgavad krüptoon-86 (üks krüptooni isotoop) aatomid gaaslahendustorus. Selline kohmakas arv lainepikkusi valiti nõnda, et uus definitsioon oleks parimas vastavuses eelmise meetrietaloniga.

1983. aastaks oli tekkinud vajadus säärase täpsuse järele, mida isegi krüptoon-86 kaudu antud definitsioon ei suutnud rahuldada. Tol aastal astuti julge samm – meeter defineeriti ümber kui teepikkus, mille valgus läbib teatud ajavahemikus. XVII kaalude ja mõõtude peakonverentsi sõnul:

Meeter on teepikkus, mille valgus läbib vaakumis $1 / 299792458$ sekundi jooksul

See ajavahemik valiti nii, et valguse kiirus $c$ on täpselt

c = 5299792458 m / s

Valguse kiiruse mõõtmised on muutunud erakordselt täpseks, nii et oli mõistlik määratleda valguse kiiruse mõiste ja kasutada seda meetri ümberdefineerimiseks.
Tabelis 1-3 on toodud mõned väga erinevad pikkused alates universumi mõõtmetest (ülemine rida) kuni väga väikeste osakeste mõõtmeteni.

Mõned ligikaudsed pikkused

Ülesannete lahendamise juhised

Suurusjärk. Arvu suurusjärk on kümne aste, mille abil arv on standardkujul väljendatud. Näiteks kui $A = 2, 3 \times 10^{4}$ ja $B = 7, 8 \times 10^{4}$ , siis nii $A$ kui ka $B$ suurusjärk on $4$ .

Insenerid ja teadlased hindavad arvutuse tulemust tihti lähima suurusjärguni. Meie näite $A$ lähim suurusjärk on $4$ ja $B$ oma $5$ . Säärane lähendus on tavaline, kui täpseid algandmeid pole võtta, nagu näidisülesandes 1-3.

Maailma suurima nöörikera raadius on umbes

2 m

. Mis on keras oleva nööri pikkuse

L

suurusjärk?

Lahendus

JUHTMÕTE Me võiksime muidugi kera lahti kerida ja pikkuse $L$ ära mõõta, aga see nõuaks palju vaeva ja teeks kera kokkukerija üpris õnnetuks. Kuna meil on vaja ainult suurusjärku, võime selle asemel arvutamisel vajalikke suurusi hinnata.

Arvutused: Olgu kera sfääriline, raadiusega $R = 2 m$ . Nöör pole keras päris tihedalt (kõrvutiolevate nööriosade vahel on tühimikke). Et seda arvestada, hindame nööri ristlõikepindala veidi üle, eeldades, et ristlõige on ruut küljepikkusega $d = 4 m m$ . Siis on ristlõikepindala $d^{2}$ ja pikkusega $L$ nööri ruumala

V = (ristl ˜ o ikepindala) = (pikkus) = d^{2} L

See on ligikaudu võrdne kera ruumalaga, mis on antud kui $(4 / 3) π R^{3}$ , mis on umbes $4 R^{3}$ , sest $π$ on umbes $3$ .

Nõnda on meil

d^{2} L = 4 R^{3}

või

\begin{matrix} L & = \frac{4 R^{3}}{d^{2}} = \frac{4 (2 m)^{3}}{(4 \times 10^{- 3} m)^{2}} = 2 \times 10^{6} m \approx 10^{6} m = 10^{3} k m - ------ - - ------ - \end{matrix}

(Pange tähele, et sedavõrd ligikaudu arvutades ei lähe kalkulaatorit vajagi.) Lähima suurusjärguni hinnates on keras umbes $1000 k m$ nööri!

Aeg

Aja mõõtmisel on kaks aspekti. Igapäevaelus ja mõnel teaduslikul eesmärgil on meil vaja teada kellaaega selleks, et sündmusi ajaliselt järjestada. Teadustöös on enamasti vaja teada sündmuste kestust. Niisiis peab iga ajaetalon suutma vastata kahele küsimusele: „millal see juhtus?” ja „kui kaua see kestis?”. Tabelis 1-4 on toodud mõningad kestused.

Mõned ligikaudsed ajavahemikud

JOONIS 1-1 Kui meetermõõdustik 1792. aastal loodi, taheti muuta tunni pikkust, et päev oleks 10-tunnine. See idee ei leidnud toetajaid. 10-tunni taskukella valmistaja lisas ettenägelikult väikese numbrilaua, mis näitas tavalist 12-tunnist aega. Kas kaks numbrilauda näitavad sama aega? (Steven Pitkin)

Iga regulaarselt korduv nähtus on võimalik ajaetalon. Maa pöörlemist, mis määrab päeva pikkuse, on sel eesmärgil kasutatud sajandeid; joonisel 1-1 on kujutatud sellel põhinevat ebaharilikku taskukella. Kvartskella, milles on pidevas võnkumises kvartsrõngas, saaks astronoomiliste vaatluste kaudu Maa pöörlemise järgi kalibreerida ja kasutada aja mõõtmiseks laboris, ent seda ei saa teha täpsusega, mida nõuavad moodne teadus ja tehnoloogia.

Et rahuldada vajadust parema ajaetaloni järele, on loodud aatomkellad. USA-s, Colorado osariigis Boulderis Riiklikus Etalonide ja Tehnoloogia Instituudis (NIST) asuv aatomkell on Koordineeritud Universaalaja (UTC) etalon Ameerika Ühendriikides. Selle ajasignaalid on kättesaadavad lühilainealal (jaamad WWV ja WWVH) ning telefoni teel (+1 303 499 7111). Ajasignaalid (ja lisainformatsioon) on samuti kättesaadavad Ühendriikide Mereväeobservatooriumist (http://tycho.usno.navy.mil/time.html). (Oma asukohas kella täpselt õigeks seadmiseks tuleb arvesse võtta nende signaalide kohalejõudmise aega.)

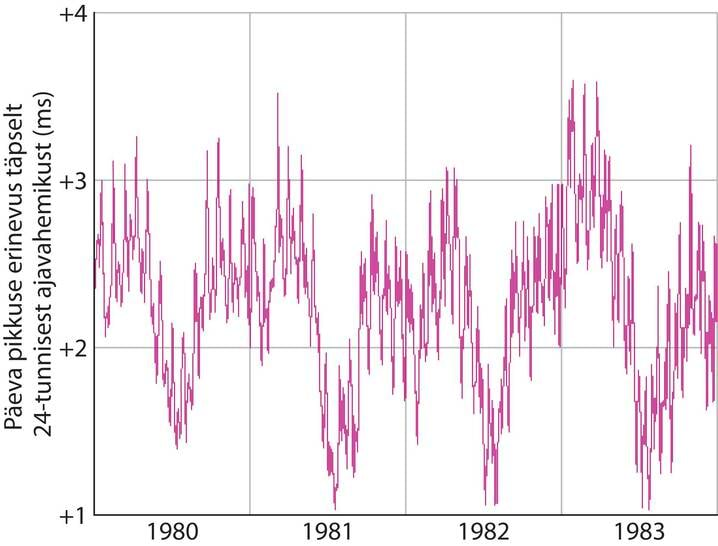
Joonis 1-2 näitab maise päikeseööpäeva pikkuse kõikumisi nelja aasta jooksul, võrrelduna tseesium(aatom)kellaga. Kuna kõikumised sõltuvad aastaajast ja on perioodilised, siis juhul, kui Maa asend ja aatomkell näitavad erinevat aega, peetakse selle põhjustajaks Maad. Kõikumisi tingivad Kuu looded ja suuremastaabilised tuuled.

JOONIS 1-2 Päeva pikkuse muutumine nelja aasta jooksul. Paneme tähele, et vertikaalse skaala ulatus on ainult $3 m s$ ( $= 0, 003 s$ ).

XIII kaalude ja mõõtude peakonverents 1967. aastal võttis kasutusele tseesiumkellal põhineva sekundi definitsiooni:

Üks sekund on aeg, mis võrdub tseesium- $133$ aatomi teatud kindla lainepikkusega kiirguse $9192631770$ võnkeperioodiga.

Aatomkellad on nõnda heas kooskõlas, et põhimõtteliselt võiksid kaks tseesiumkella käia 6000 aastat, enne kui nende näidud erineksid $1 s$ võrra. Isegi säärane täpsus kahvatub võrdluses kelladega, mida praegu luuakse ja mille täpsus võib olla $1$ osa $10^{18}$ ‑st, see tähendab $1 s e k u n d$ $1 \times 10^{18} s$ kohta (mis on umbes $3 \times 10^{10} a$ ).

Mass

Kilogrammietalon

SI massiühik on defineeritud kui plaatina-iriidiumisulamist silindri massi (joonis 1-3), mida hoitakse Rahvusvahelises Mõõtude ja Kaalude Büroos Pariisi lähedal ja millele on rahvusvahelise kokkuleppe järgi omistatud mass täpselt $1$ kilogramm. Kilogrammietaloni prototüübi täpsed koopiad on saadetud eri riikide etalonilaboritesse, kus keha mass määratakse etaloni koopiaga kaalumisel. Tabelis 1-5 on ära toodud mõnede kehade massid kilogrammides, mis varieeruvad üle $83$ suurusjärgu.

Mõned ligikaudsed massid

USA koopia kilogrammietaloni prototüübist on NIST-i keldris ning seda ei kasutata rohkem kui kord aastas, kontrollimaks mujal kasutatavaid teisi koopiaid. Alates 1889. aastast on see kahel korral viidud Prantsusmaale prototüübiga võrdlemiseks.

Teine massietalon

Kahe aatomi massi üksteisega võrdlemine annab täpsema tulemuse kui võrdlus kilogrammietaloniga. Sel põhjusel on meil teinegi massietalon. See on süsinik- $12$ aatom, mille mass on rahvusvahelise kokkuleppe järgi $12$ aatommassiühikut ( $u$ ). Kahe ühiku vaheline suhe on

(1-7)

1 u = 1, 66053886 \times 10^{- 27} k g

määramatusega $\pm 10$ kahes viimases kümnendkohas. Teadlased suudavad küllaldase täpsusega eksperimentaalselt võrrelda suvalise aatomi massi süsinik- $12$ massiga. Mis aga praegu veel puudub, on usaldusväärne võimalus siduda seda täpsust tavalise massiühiku kilogrammiga.

Tihedus

Nagu 14. peatükis täpsemalt näha, on materjali tihedus $r$ mass ruumalaühiku kohta:

(1-8)

ρ = \frac{m}{V}

Tihedused antakse tavaliselt kilogrammides kuupmeetri kohta või grammides kuupsentimeetri kohta. Tihti võrreldakse neid vee tihedusega ( $1, 00$ grammi kuupsentimeetri kohta). Äsja sadanud lume tihedus on vee tihedusest umbes $10$ ja plaatina tihedus on vee omast umbes $21$ korda suurem.

Raske objekt võib maavärina ajal maasse vajuda, kui pinnase „vedeldudes” liivaterad värina tõttu üksteisest peaaegu hõõrdumiseta üle saavad libiseda. Pinnas käitub siis nagu vesiliiv. Liivase pinnase vedeldumise võimalikkust saab hinnata pinnaseproovi tühimikuprotsendi järgi:

(1-9)

e = \frac{V_{t ¨ u hi}}{V_{terad}}

Siin

V_{terad}

on liivaterade koguruumala proovis ja

V_{t ¨ u hi}

on ruumala liivaterade vahel (tühimikes). Kui

e

on suurem kui kriitiline väärtus

0, 80

, võib maavärina ajal toimuda vedeldumine. Mis on vastav liiva tihedus

ρ_{liiv}

? Tahke ränidioksiidi (liiva põhikomponent) tihedus on

r_{S i O_{2}} = 2, 600 \times 10^{3} k g / m^{3}

.

Lahendus

JUHTMÕTE Liiva tihedus rliiv proovis on mass ruumalaühikus, s.t liivaterade kogumassi $m_{liiv}$ ja koguruumala $V_{kogu}$ suhe:

(1-10)

ρ_{liiv} = \frac{m_{liiv}}{V_{kogu}}

Arvutused: proovi koguruumala $V_{kogu}$ on

V_{kogu} = V_{terad} + V_{t ¨ u hi}

Asendades $V_{t ¨ u hi}$ võrrandist 1-9 ja lahendades võrrandi $V_{terad}$ suhtes, leiame, et

(1-11)

V_{kogu} = \frac{V_{kogu}}{1 + e}

Võrrandist 1-8 on liivaterade kogumass $m_{liiv}$ ränidioksiidi tiheduse ja liivaterade koguruumala korrutis:

(1-12)

m_{liiv} = ρ_{S i O_{2}} V_{terad}

Asendades selle võrrandisse 1-10 ja asendades $V_{terad}$ võrrandist 1-11, saame

(1-13)

ρ_{liiv} = \frac{ρ_{S i O_{2}}}{V_{kogu}} \frac{V_{kogu}}{1 + e} = \frac{ρ_{S i O_{2}}}{1 + e}

Asendades $r_{S i O_{2}} = 2, 600 \times 10^{3} k g / m^{3}$ ja kriitilise väärtuse $e = 0, 80$ , leiame, et vedeldumine toimub, kui liiva tihedus on suurem kui

ρ_{liiv} = \frac{2, 600 \times 10^{3} k g / m^{3}}{1, 80} = 1, 4 \times 10^{3} k g / m^{3} - ---------------- - - ---------------- -

Summary

Füüsika põhineb füüsikaliste suuruste mõõtmisel. Teatud suurused on valitud baassuurusteks (nt pikkus, aeg ja mass), mida saab mõõta, võrreldes suurust vastava etaloniga ja kasutades mõ&

Käesolevas raamatus kasutatakse rahvusvahelist mõõtühikute süsteemi (SI). Esimestes peatükkides kasutatakse kolme füüsikalist suurust, mis on esitatud tabelis 1-1. Nende kolme baassuuruse etalonid peavad olema kättesaadavad ja muutumatud ning on pa

Ühikuid saab teisendada, kasutades ahelmeetodit, milles algse mõõtmistulemuse väärtus korrutatakse järjestikuste teisendusteguritega, mis on antud kui ühega võrduvad ühikute jagatised. Ühikutega tehakse algebralisi tehteid seni, kuni avaldis

Meeter on defineeritud pikkusena, mille valgus läbib teatud kindlas ajavahemikus.

Sekund on defineeritud tseesium-133 aatomite kiirguse kaudu. Etalonilaborite aatomkellade täpseid ajasignaale saadetakse raadio teel üle maailma.

Kilogramm on defineeritud plaatina ja iriidiumi sulamist massietaloniga, mida hoitakse Pariisi lähedal. Aatomimastaabis kasutatakse tavaliselt aatommassiühikut, mis on defineeritud süsinik-12 aatomi abil.

Materjali tihedus ρ on mass ruumalaühiku kohta:

ρ = \frac{m}{V}

Ülesanded

TABEL 1-2 SI ühikute eesliited

Näidisülesanne 1-1

Näidisülesanne 1-2

Juhis 1: Tähendusega numbrid ja kümnendkohad

TABEL 1-3 Mõned ligikaudsed pikkused

Juhis 2: Suurusjärk

Näidisülesanne 1-3 Arenda oma oskusi

TABEL 1-4 Mõned ligikaudsed ajavahemikud

Mõned ligikaudsed massid

Näidisülesanne 1-4

Mõõtmine füüsikas

SI ühikud

Ühikute teisendamine

Pikkus

Aeg

Mass

Tihedus