Lennukid II

Sissejuhatus

Me peame uurima võimalusi lennuliikluse efektiivsemaks muutmiseks ning selliste uute kütuste välja töötamiseks, mis lubaksid meil vähem kütust põletada ning vähem saastada.
Tony Blair

Parimale lootma jäämine ei ole poliitiline otsus, see on hullumeelsus.
Emily Armistead, Greenpeace

Millised on lendamisega seotud põhimõttelised piirangud? Kas lendamise füüsika määrab pääsematult ära iga lennukilomeetri või lennukiga transporditud tonni kohta kuluva energiahulga? Milline on maksimaalne vahemaa, mille suudab läbida $300$ tonni kaaluv Boeing 747? Aga $1$ kilogrammi kaaluv vöötsaba-vigle või $100$ -grammine randtiir?

Täpselt nii, nagu peatükis Autod II hindasime autode poolt kulutatud energiat, pakkudes mudelit ja vastuseid küsimusele „kuhu autos energia kulub?“ on selle peatüki teemaks lennukid ning me otsime vastust küsimusele „kuhu lennates energia kulub?“ Ainuke füüsika, mida sellele küsimusele vastamiseks vajame, on Newtoni seadused -vajaduse tekkides kirjeldan ma neid ka lähemalt.

See mõtterada annab vastuse sellistele küsimustele nagu „kas kulutaksime lendamisel vähem energiat kui kasutaksime aeglasemaid propelleritega lennukeid?" Meid ootab ees palju valemeid, loodan, et te naudite neid!

Joonis C.1: Linnud: kaks randtiiru, vöötsaba-vigle ja Boeing 747.

Kuidas lennata

Lennukid (ja linnud) liiguvad läbi õhu, nii et sarnaselt autode ja rongidega mõjub neile õhutakistus ja enamus lennukite poolt neelatavast energiast kulub nende lükkamisele läbi õhu, ületades selleks õhutakistuse tekitatud jõu. Lisaks sellele peavad lennukid erinevalt autodest ja rongidest kulutama energiat õhus püsimiseks.

Lennukid püsivad õhus (üleval), sest paiskavad õhku alla. Kui lennuk surub õhku alla, surub õhk lennukit üles (sest Newtoni kolmas seadus ütleb seda). Lennuk ei söösta alla, kui see ülespoole suunatud jõud, mida kutsutakse tõstejõuks, tasakaalustab allapoole suunatud raskusjõu.

Kui lennuk paiskab õhku alla, saab õhk kineetilist energiat. Nii et tõstejõu tekitamine nõuab energiat. Lennuki lendamiseks vajalik koguenergia on tõstejõu tekitamiseks vajaliku energia ja tavapärase õhutakistuse ületamiseks vajaliku energia summa. (Muide, tõstejõu tekitamiseks vajalikku võimsust nimetatakse tavaliselt indutseeritud takistuseks. Aga mina kutsun seda tõstejõu võimsuseks, $P_{lift}$ .)

Lendamise teooria läbitöötamiseks on meil vaja kahte võrrandit: Newtoni teist seadust:

(C.1)

j ˜ o ud = impulsi muutumise kiirus

ja Newtoni kolmandat seadust, mida just mainisin:

(C.2)

A poolt B-le avaldatav j ˜ o ud = - B poolt A-le avaldatav j ˜ o ud

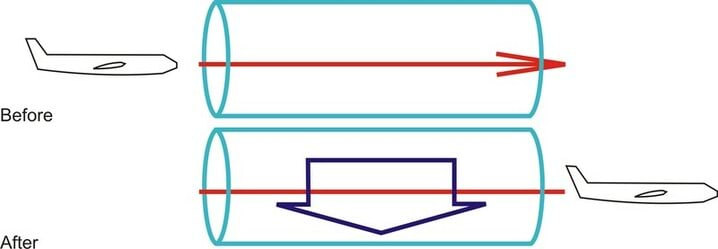
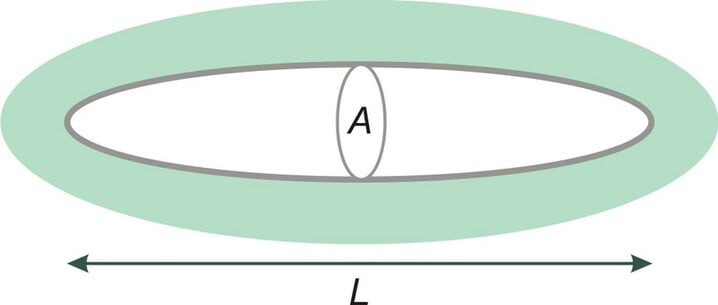
Ütlen selle loo puändi ära neile, kellele valemid üldse ei meeldi: me saame teada, et tõstejõu tekitamiseks vajaminev võimsus on võrdne võimsusega, mida on vaja takistusjõu ületamiseks. Nii et vajadus „püsida õhus" kahekordistab vajamineva võimsuse. Teeme joonise kiirusega $v$ lendavale lennukile mõjuvast tõstejõust. Aja $t$ jooksul liigub lennuk vahemaa $v t$ ja jätab enda taha allapoole liikuva õhusilindri (joonis C.2).

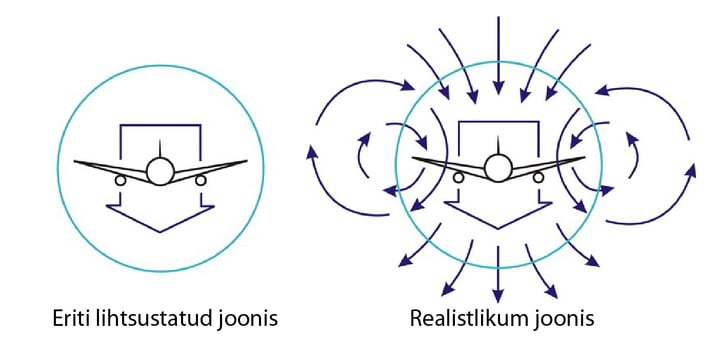
Joonis C.2: Lennuk lendab läbi paigalseisva õhu silindri. Lennuki läbimisel surutakse õhk selles allapoole. Jõud, millega lennuk mõjub allapoole suunatud õhule on võrdne ja vastassuunaline jõuga, millega mõjub õhk lennukile.

Me tähistame selle õhusilindri ristlõikepindala kui $A_{v}$ . Silindri diameeter on ligikaudu võrdne lennuki tiivaulatusega $w$ . (Selle suure silindri sees on väiksema diameetriga keeriseid ja turbulentse sisaldav silinder, mille ristlõike pindala on ligikaudu võrdne lennuki esiotsa pindalaga.) Tegelikult on õhu voolamine palju huvitavam kui see silindri pilt: iga tiib jätab enda taha keerise, kus tiiva all olev õhk liigub kiiresti alla ja õhk tiiva otstest kaugemal liigub üles (joonised C.3 C.4).

Joonis C.3: Meie mudel eeldab, et lennuk jätab enda taha allapoole liikuva õhu silindri. Tegelikult on pilt keerulisem ja sisaldab keeriseid. Reaalset asja saab vaadata jooniselt C.4.

Joonis C.4: Õhu voolamine lennuki taga. Foto NASA Langley Research Centre

Seda ülespoole liikuvat õhku kasutavad ära linnud, kui nad lendavad V-kujulistes parvedes: täpselt tiiva otsa taga on kena väike tõusev õhuvool. Aga pöördume tagasi õhusilindrite juurde.

Silindris oleva õhu mass on

(C.3)

m_{silinder} = tihedus \times ruumala = ρ v t A_{v}

Oletame, et kogu õhusilinder liigub allpoole kiirusega $u$ , ja leiame, kui suur peab $u$ olema selleks, et tekkiv tõstejõud tasakaalustaks lennukile mõjuva raskusjõu $m g$ . Aja $t$ jooksul tekkinud õhusilindri allapoole suunatud impulss on

(C.4)

mass \times kiirus = m_{silinder} u = ρ v t A_{s} u

Ja Newtoni seaduste kohaselt peab see impulss olema võrdne lennukile selle kaalu poolt antud impulsiga

(C.5)

m g t

Teisendades nii saadud võrrandit

(C.6)

ρ v t A_{s} u = m g t

saame avaldada õhusilindri allapoole suunatud kiiruse

(C.14)

u = \frac{m g}{ρ v A_{s}}

See on huvitav! Õhusilindri kiirus on pöördvõdeline lennuki kiirusega $v$ . See tähendab, et aeglaselt liikuv lennuk peab võrreldes kiire lennukiga õhusilindrit tugevamalt allapoole suunama, sest ajaühikus läbib lennuk lühema õhusilindri. See on ka põhjus, miks aeglaselt liikuvad maanduvad lennukid peavad oma klappe suurendama: nii tekivatavad nad suuremad ja järsemad tiivad, mis suunavad õhusilindrit tugevamalt allapoole.

Kui palju kulub energiat õhusilindri nõutud kiirusega $u$ allapoole surumiseks? Vajalik võimsus on

(C.7 - C.10)

\begin{matrix} P_{t ˜ o ste} & = \frac{silindri kineetiline energia}{a e g} = \frac{1}{t} \frac{1}{2} m_{silinder} u^{2} = \frac{1}{2 t} ρ v t A_{s} (\frac{m g}{ρ v A_{s}})^{2} = \frac{1}{2} \frac{(m g)^{2}}{ρ v A_{s}} \end{matrix}

Lennuki liigutamiseks vajalik koguvõimsus on takistusjõu võimsuse ja tõstejõu võimsuse summa:

(C.11 - C.12)

\begin{matrix} P_{kogu} & = P_{takistus} + P_{t ˜ o ste} = \frac{1}{2} c_{d} ρ A_{p} v^{3} + \frac{1}{2} \frac{(m g)^{2}}{ρ v A_{s}} \end{matrix}

kus $A_{p}$ on lennuki esipinna pindala ja $c_{p}$ on õhutakistustegur (nagu ka peatükis Autod II). Lennuki kütuse kasutamise kasutegur, väljendatuna läbitud tee kohta kulutatud energiana, on:

(C.13)

\frac{energia}{vahemaa} {∣ ∣ ∣}_{ideaal} = \frac{P_{kogu}}{v} = \frac{1}{2} c_{d} ρ A_{p} v^{2} + \frac{1}{2} \frac{(m g)^{2}}{ρ v^{2} A_{s}}

seda juhul, kui lennukikütuse energia muudetakse ideaalselt, st kadudeta tõukejõuks ja tõstejõuks. (Muide, „energia läbitud teepikkuse kohta" on jõud ja kaks liiget valemis on tegelikult takistusjõud $\frac{1}{2} c_{d} ρ A_{p} v^{2}$ ja tõstejõud $\frac{1}{2} \frac{(m g)^{2}}{ρ v^{2} A_{s}}$ . Nende kahe jõu summa on „tõukejõud", mis näitab, kui tugevalt peavad mootorid tõukama.)

Reaalsete reaktiivmootorite kasutegur on umbes $ε = \frac{1}{3}$ , nii et kiirusel $v$ lendava lennuki poolt teepikkuse kohta kulutatud energia on

(C.14)

\frac{e n e r g i a}{v a h e m a a} = \frac{1}{ε} (\frac{1}{2} c_{d} ρ A_{p} v^{2} + \frac{1}{2} \frac{(m g)^{2}}{ρ v^{2} A_{s}})

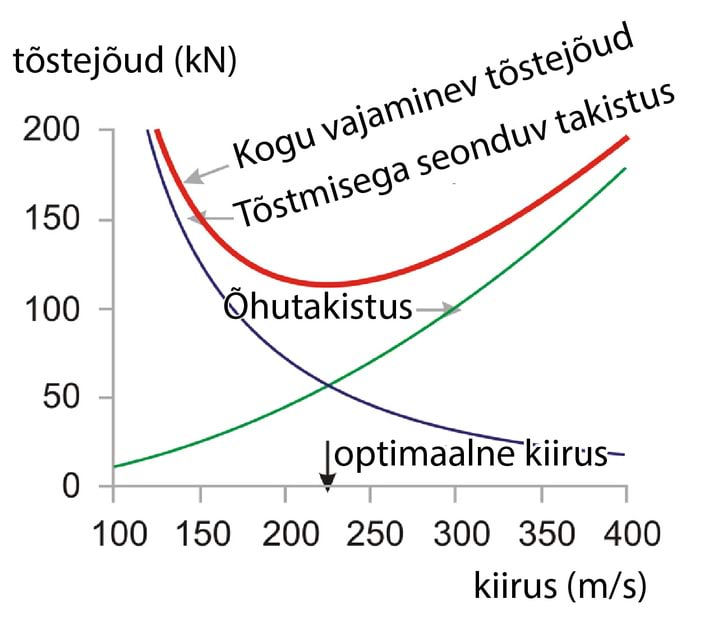
Selline teepikkuse kohta kulutatud energia avaldis on üsna keeruline, aga see lihtsustub oluliselt, kui me eeldame, et lennuk on ehitatud lendama kiirusel, millel teepikkuse kohta kulutatav energia on minimaalne. Sest kui vaadata teepikkuse kohta kulutatavat energiat kiiruse $v$ funktsioonina, siis on sellel üks hea koht (joonis C.5).

Joonis C.5: Lennuki liikumas hoidmiseks vaja minev energia sõltuvana kiirusest $v$ on takistusjõu $\frac{1}{2} c_{d} ρ A_{p} v^{2}$ – mis suureneb kiiruse kasvades – ja tõstmiseks kuluva jõu (tuntud ka kui indutseeritud takistus) $\frac{1}{2} \frac{(m g)^{2}}{ρ v^{2} A_{s}}$ – mis väheneb kiiruse suurenedes – summa. Ón olemas kiirus $v_{optimaalne}$ , mille korral vajalik jõud on minimaalne. Jõud on energia teepikkuse kohta, nii et minimiseerides jõu minimiseerime me ka teepikkuse kohta kuluva kütuse hulga. Et kütuse kasutust optimiseerida peame me lendama kiirusel $v_{optimaalne}$ . See joonis näitab kilonjuutonites meie lihtsa mudeli hinnangut, millist jõudu on erinevate kiiruste $v$ korral tarvis $317$ tonni kaaluva, $64$ -meetrise tiivaulatusega, $0, 03$ takistuskoefitsiendiga ja $180 m^{2}$ esiosa pindalaga Boeing 474 lendamiseks, kui õhutihedus on $ρ = 0, 41 k g / m^{3}$ ( $10 k m$ kõrgusel). Meie mudel pakub optimaalseks kiiruseks $v_{optimaalne} = 220 m / s$ ( $540 m i i l i / t$ ). Õhusilindriga tegeleva mudeli jaoks on see võrdluses tegelikkusega väga hea tulemus!

Suuruste $\frac{1}{2} c_{d} ρ A_{p} v^{2}$ ja $\frac{1}{2} \frac{(m g)^{2}}{ρ v^{2} A_{s}}$ summal asub miinimum kohas, kus need kaks suurust on võrdsed. See nähtus on füüsikas ja inseneerias rõõmustavalt sagedane: kaks suurust, mis justkui ei peaks võrdsed olema, on seda siiski, või siis erinevad üksteisest kaks korda.

Niisiis, see võrdsuse printsiip ütleb meile, et lennuki optimaalne kiirus on selline, et kehtiks

(C.15)

c_{d} ρ A_{p} v^{2} = \frac{(m g)^{2}}{ρ v^{2} A_{s}}

(C.16)

ρ v_{optimaalne}^{2} = \frac{m g}{\sqrt{c_{d} A_{p} A_{s}}}

Kui meie lennuki lihtsustatud mudel on õige, siis defineerib selline avaldis lennuki optimaalse kiiruse: mudel ei tööta, kui mootorite efektiivsus $ε$ sõltub olulisel määral kiirusest või kui lennuki kiirus ületab helikiirust ( $330 m / s$ ); ülehelikiirustel vajame takistuse ja tõste jaoks erinevat mudelit.

Kontrollime oma mudelit ja vaatame, mida see ennustab 747 ja albatrossi optimaalseks kiiruseks. Peame olema tähelepanelikud ja arvestama õige õhutihedusega: kui tahame hinnata 747 optimaalset kiirust $3000$ jala kõrgusel, siis peame arvestama, et õhu tihedus kõrguse $z$ kasvades käitub nagu $e x p (\frac{- m g z}{k T})$ , kus $m$ on lämmastiku ja hapniku molekulide mass ja $k T$ on soojusenergia (Boltzmanni konstant korda absoluutne temperatuur). Õhutihedus sellel kõrgusel on ligikaudu $3$ korda väiksem.

Ennustatud optimaalsed kiirused (vt tabel) on täpsemad, kui meil oleks põhjust oodata! 747 optimaalseks kiiruseks saame $540 m i i l i / t$ ja albatrossile $32 m i i l i / t$ – mõlemad väärtused on väga lähedal nende lindude tõelistele lennukiirustele (vastavalt $560 m i i l i / t$ ja $30$ – $55 m i i l i / t$ ).

Tabel 4.8: Lennuki ja albatrossi optimaalse kiiruse hinnangud.

Lind		747	Albatross
Konstruktor		Boeing	looduslik valik
Mass (täislast)	$m$	$363000 k g$	$8 k g$
Tiivaulatus	$w$	$64, 4 m$	$3, 3 m$
Pindala^∗	$A_{p}$	$180 m^{2}$	$0, 09 m^{2}$
Tihedus	$ρ$	$0, 4 k g / m^{3}$	$1.2 k g / m^{3}$
Takistustegur	$c_{d}$	$0, 03$	$0, 1$
Optimaalne kiirus	$v_{opt}$	$220 m / s = 540 m i i l i / t$	$14 m / s = 32 m i i l i / t$

*747 esiosa pindala hindamiseks on võetud selle kabiini laius ( $6.1 m$ ) ja korrutatud see kere ligikaudse kõrgusega ( $10 m$ ), pärast seda on tulemus tiibade, mootorite, ja saba arvestamiseks korrutatud kahega. Albatrossi esiosa pindala hinnang on saadud fotodelt.

Teeme oma mudeli põhjal veel mõned ennustused. Me saame näiteks kontrollida, kas valemist C.13 leitud jõud on samasugune, kui 747 reaalne tõukejõud. Teades, et optimaalse kiiruse korral on seal kaks jõudu (tõukav ja lennukit õhus hoidev) võrdsed, peame lihtsalt ühe välja valima ja selle kahega korrutama:

(C.17-C.20)

\begin{matrix} j ˜ o ud = \frac{e n e r g i a}{v a h e m a a} {∣ ∣ ∣}_{ideaal} & = \frac{1}{2} c_{d} ρ A_{p} v^{2} + \frac{1}{2} \frac{(m g)^{2}}{ρ v^{2} A_{s}} = c_{d} ρ A_{p} v_{opt}^{2} = c_{d} ρ A_{p} \frac{m g}{ρ (c_{d} A_{p} A_{s})^{\frac{1}{2}}} = (\frac{c_{d} A_{p}}{A_{s}})^{\frac{1}{2}} m g \end{matrix}

C.7: Boeing 747 eestvaade, mille abil me hindame lennuki esiotsa pindala $A_{p}$ . Ruudu pindala on $A_{s}$ (tiivaulatuse ruut).

Defineerime pindalade suhte $f_{A}$ :

(C.21)

f_{A} = \frac{A_{p}}{A_{s}}

(Mõelge sellest kui joonisel C.7 kujutatud ruudu lennuki poolt hõivatud osast.) Siis

(C.22)

j ˜ o ud = (c_{d} f_{A})^{\frac{1}{2}} (m g)

Huvitav! Nõutud tõukejõud ei sõltu selle keskkonna tihedusest, milles lennuk lendab (eeldades, et lennuk lendab optimaalse kiirusega), ja võrdub dimensioonitu konstandi ( $c_{d} f_{A}^{\frac{1}{2}}$ ) ja lennuki kaalu korrutisega. Muide, see konstant on tuntud kui lennuki takistusjõu ja tõstejõu suhe (drag-to-lift ratio või glide number). (Tõstejõu ja takistusjõu suhet nimetatakse eesti keeles aerodünaamiliseks väärtuseks, selle tüüpilised väärtused on esitatud tabelis.)

Tabel 4.9: Lindude tõstejõu ja takistusjõu suhted.

Airbus A320	$17$
Boeing 767-200	$19$
Boeing 747-100	$18$
Jõgitiir	$12$
Albatross	$20$

Boeing 747 kohta käivate arvude põhjal ... ja ... ning seega on vajaminev tõukejõud

(C.23)

(c_{d} f_{A})^{\frac{1}{2}} (m g) = 0, 036 m g = 130 k N

Joonis C.9: Cessna 310N: $60 k W h$ $100$ reisija-kilomeetri kohta. Cessna 310 Turbo liigutab kiirusega $370 k m / h$ kuute reisijat (seehulgas pilooti). Foto: Adrian Pingstone.

Kui lähedal on see tulemus 747 tehnilistele andmetele? Tegelikkuses on kõigi nelja mootori maksimaalne tõukejõud ligikaudu $250 k N$ , kuid seda maksimaalväärtust kasutatakse vaid õhkutõusu ajal. Reisilennu tavakõrgusel on vajatav tõukejõud palju väiksem: 747 keskmine tavakõrguse tõukejõud on $200 k N$ – see on meie poolt joonise abil ennustatud väärtusest vaid $50 %$ rohkem. Meie lihtne mudel on veidi ebatäpne, sest alahindasime takistusjõu ja tõstejõu suhet.

Selle tõukejõu abil saame leida otseselt ükskõik millise lennuki transpordiefektiivsuse. Võimalik on arvutada välja kahte sorti transpordiefektiivsust: massi liigutamise energiakulu, mida mõõdetakse ühikutes $k W h$ tonn-kilomeetri kohta, ning inimeste liigutamise energiakulu, mida mõõdetakse ühikutes $k W h$ $100$ reisija-kilomeetri kohta.

Massi transportimise efektiivsus

Tõukejõud on jõud ehk energia ühikpikkuse kohta. Ühikpikkuse läbimiseks kuluv koguenergia korrutatakse teguriga $1 / ε$ kus $ε$ on mootori efektiivsus, mille väärtuseks võtame $1 / 3$ .

Kogu transpordikulu ehk energia, mis kulub (kogu lennuki) ühikmassi liigutamiseks ühikulise pikkusega vahemaa võrra, on:

(C.24-C.26)

\begin{matrix} transpordikulu & = \frac{1}{ε} \frac{j ˜ o ud}{mass} = \frac{1}{ε} \frac{(c_{d} f_{A})^{\frac{1}{2}} m g}{m} = \frac{(c_{d} f_{A})^{\frac{1}{2}}}{ε} g \end{matrix}

Seega on transpordikulu lihtsalt üks ühikuta suurus (mis sõltub lennuki kujust ning mootori efektiivsusest), mis korrutatakse $g$ ehk gravitatsioonikiirendusega. Pangem tähele, et see transpordi kogukulu kehtib kõikidele lennukitele, kuid sõltub vaid lennuki kolmest lihtsast omadusest: selle hõõrdetegurist, kujust ning mootori efektiivsusest. See ei sõltu aga üldse lennuki suurusest ning kaalust ja kohe üldse mitte õhutihedusest. Kui me kasutame $ε$ väärtusena $1 / 3$ ning eeldame, et takistus- ja tõstejõu suhe on $20$ , siis leiame, et ükskõik millise lennuki transpordi kogukulu on vastavalt meie mudelile

0, 15 g

ehk

0, 4 kWh/tonn-km

Kas on võmalik ehitada efektiivsemaid lennukeid?

Joonis C.10: „Kinnitage turvavööd.“ 8 reisijaga Bombardier Learjet 60XR, lennukiirusega $780 k m / h$ – transpordikulu $150 k W h$ $100$ reisija-kilomeetri kohta.

Kui lennukite efektiivsust saab tulevaste tehnoloogiliste läbimurrete abil vaid veidi parandada ning kui nende kuju on juba praegu praktiliselt täiuslik, siis ei saa me seda ühikuta suurust eriti palju paremaks muuta. Transpordi efektiivsus on juba praegu oma füüsikalisele piirile lähedal. Aerodünaamika asjatundjate sõnul saaks lennukite kuju veidi parandada, kui võtaksime kasutusele ühendatud tiibadega kered (ingl k blended-wing bodies). Hõõrdetegurit saaks veidi vähendada laminaarse voolukontrolli abil – selle tehnoloogia abil saaks tiiva kohal tekkivat turbulentsi vähendada tiiva pinnal asuvatest väikestest aukudest õhu sissepumpamise abil (Braslow, 1999). Olemasolevatele lennukitele laminaarse voolukontrolli tehnoloogia lisamisega väheneks hõõrdetegur $15 %$ võrra ning ühendatud tiibadega lennukikerede abil eelduste kohaselt $18 %$ võrra (Green, 2006). Valem (C.26) ütleb meile, et transpordikulu on võrdeline hõõrdeteguri ruutjuurega, mistõttu kahaneks $c_{d}$ $15$ - ja $18$ -protsendilise vähenemise tõttu transpordikulu vastavalt $7, 5 %$ ja $9 %$ võrra.

See transpordi kogukulu on energia, mis kulub massi liigutamisele – siia alla käib ka lennuki enda mass. Et leida kaupade liigutamiseks kuluv energiahulk kauba ühikmassi kohta, tuleb meil eelnevalt leitud suurus jagada kauba osakaalu näitava murdarvuga. Kui 747 kogumassist näiteks $1 / 3$ moodustab kaup, siis on selle transpordikulu

0, 45 g

ehk ligikaudu $1, 2 kWh/tonn-km$ . See on tavalise kaubaveoki transpordikulust ( $1 kWh/tonn-km$ ) vaid veidi suurem.

Inimeste transportimise efektiivsus

Sarnaselt saame hinnata ka 747 reisijate transportimise efektiivsust.

(C.27-C.30)

Transpordi efektiivsus (reisija-km 1 liitri k ¨ u tuse kohta) = \begin{matrix} = reisijate arv \times \frac{energia liitri kohta}{\frac{t ˜ o ukej ˜ o ud}{ε}} = reisijate arv \times \frac{ε \times energia liitri kohta}{t ˜ o ukej ˜ o ud} = 400 \times \frac{1}{3} \frac{38 M J / l i i t e r}{200000 N} = 25 reisija-km liitri kohta \end{matrix}

See on ühe liitri kütuse kohta veidi efektiivsem kui tavaline ühe reisijaga auto (kütusekulu $12 k m$ liitri kohta). Seega on lennukiga lendamine energia poolest efektiivsem kui autosõit olukorras, kus autos on vaid üks või kaks reisijat. Autosõit on efektiivsem, kui selles on kolm või enam reisijat.

Olulised punktid

See oli päris pikk arutelu! Võtame põhiideed kiirelt kokku. Pool lennuki poolt tehtavast tööst kulub õhus püsimiseks, teine pool kulub edasi liikumiseks. Optimaalsel kiirusel lendamise kütuseefektiivsuse (energia läbitud vahemaa kohta) leidsime jõu abil (C.22) – see oli võrdeline lennuki kaaluga. Seda võrdetegurit nimetatakse takistusjõu ja tõstejõu suhteks ning see sõltub lennuki kujust.

Seega – kuigi autosõidu kiiruspiirangute vähendamine kahandaks ühikulise teepikkuse läbimiseks kuluvat energiahulka, ei ole kiiruspiirangute kasutamine lennukite puhul eriti mõttekas. Igal õhus lendaval lennukil on oma optimaalne kiirus, mis on iga lennuki jaoks erinev, sõltudes selle kaalust – lennukid lendavad oma optimaalse kiirusega juba praegu. Kui otsustaksime, et lennukid peaksid lendama aeglasemalt, nende energiakulu hoopiski suureneks. Ainus viis lennukeid efektiivsemalt kütust põletama panna oleks käskida neil maanduda ning paigale jääda. Lennukite tehnoloogiat on läbi aegade kõvasti täiustatud ning tulevikus suurt efektiivsuse kasvu ilmselt ei saavutata. (Lehekülgedel 37 ja 132 on arutatud selle üle, kas uued hiigellennukid on vanematest hiigellennukitest tõepoolest „palju efektiivsemad“ ning kas turbomootorid on „palju efektiivsemad“ kui reaktiivmootorid.)

Joonis C.11: Boeing 737-700: 30 kWh 100 reisija-kilomeetri kohta.

Lennuulatus

Veel üks võimalus midagi ennustada on leida lennuki või linnu lennuulatus – suurim vahemaa, mille see saab ilma kütust tankimata lennata. Võiks arvata, et suuremate lennukite lennuulatus on suurem, kuid meie mudeli abil tehtav ennustus on üllatavalt lihtne. Lennuki lennuulatus ehk maksimaalne vahemaa, mille see saab ilma kütust juurde tankimata läbida, on võrdeline selle kiiruse ning kütuse koguenergiaga ning pöördvõrdeline selle kütusekuluga:

(C.31)

\begin{matrix} Lennuulatus & = v_{opt} \times energia v ˜ o imsus = \frac{energia \times ε}{j ˜ o ud} \end{matrix}

Kütuse koguenergia all peame silmas kütuse kütteväärtuse $C$ (džaulides kilogrammi kohta) ning massi korrutist. Kütuse mass moodustab mingi murdosa $f_{k ¨ u tus}$ lennuki kogumassist. Seega

(C.32)

\begin{matrix} Lennuulatus & = \frac{energia \times ε}{j ˜ o ud} = \frac{C m ε f_{k ¨ u tus}}{(c_{d} f_{A})^{\frac{1}{2}} (m g)} = \frac{ε f_{k ¨ u tus}}{(c_{d} f_{A})^{\frac{1}{2}} g} \end{matrix}

Veelgi lihtsamat ennustust on raske ette kujutada: mingi linnu või lennuki lennuulatus on mootori efektiivsusest, hõõrdetegurist ning linnu kujust sõltuva ühikuta teguri ... ning fundamentaalse vahemaa

\frac{C}{g}

korrutis. See viimane tegur sõltub vaid kütusest ning gravitatsioonist – linnu suurus, mass, pikkus, laius ning keskkonna tihedus ei oma selle puhul tähtsust.

Mis maagiline vahemaa see selline on? See vahemaa on sama nii hanerasva kui reaktiivkütuse puhul: mõlemad kütused on oma olemuselt süsivesinikud $(C H_{2})_{n}$ . Reaktiivkütuse kütteväärtus $C = 40 M J / k g$ . Reaktiivkütuse jaoks on see vahemaa

(C.33)

d_{k ¨ u tus} = \frac{C}{g} = 4000 k m

Linnu puhul tuleb see väärtus, $4000 k m$ , korrutada teguriga

(\frac{ε f_{k ¨ u tus}}{(c_{d} f_{A})^{\frac{1}{2}}})

Kui meie linnu mootori efektiivsus on $ε = 1 / 3$ ning takistus- ja tõstejõudude suhe on

(c_{d} f_{A})^{\frac{1}{2}} ≃ \frac{1}{20}

ning kui peaaegu pool linnu massist moodustab selle kütus (täiskoormaga Boeing 747 massist moodustab kütus $46 %$ ), siis leiame, et ükspuha millise suurusega linnu või lennuki jaoks on lennuulatus sama: umbes kolm korda suurem kui kütuse vahemaa: ligikaudu $13000 k m$ .

Võime tegurist $d_{k ¨ u tus}$ mõelda kui vahemaast, mille kaugusele kütus ennast viiks, kui see suudaks järsku muundada kogu oma keemilise energia kineetiliseks energiaks ning heita end paraboolsel trajektooril õhku, millel puudub takistus. (Täpsemini öeldes on optimaalse parabooltrajektoori abil saavutatav vahemaa tegurist $C / g$ kaks korda suurem.) See vahemaa on ka sama mis vertikaalne kõrgus, milleni kütus hüppaks juhul, kui puuduks õhutakistus. Lisaks on põnev tähele panna, et kütuse kütteväärtus $C$ , mille ma esitasin ühikutes džauli kilogrammi kohta, on esitatav ka kiiruse ruuduna (täpselt nagu energia ja massi suhe $E / m$ Einsteini kuulsas valemis $E = m c^{2}$ sisaldab kiiruse ruutu $c^{2}$ ): $40 \times 10^{6} J / k g$ on sama mis $(6000 m / s)^{2}$ . Seega võime rasvast mõelda järgnevalt: „rasv tähendab $6000$ meetrit sekundis.“ Kui soovite sörkimise abil kaalu kaotada – ning seda vaid ühe korraga – tuleks teil joosta kiirusega $6000 m / s$ ( $12000 m i i l i / t$ ).

Ka see suurus on täpsele väärtusele üpriski lähedal: Boeing 747 pikima lennu rekord (23-24 märts 1989) on $16560 k m$ .

Ning väidet, mille kohaselt lennuulatus ei sõltu linnu suurusest, kinnitavad vaatlusandmed: igas suuruses linnud, nii suured haned kui ka väikesed pääsulased ja randtiirud, rändavad kontinentidevahelisi vahemaid. Pikim mõõdetud linnu poolt peatusteta läbitud vahemaa on $11000 k m$ – selle lendas vöötsaba-vigle.

Kui kaugele lendas Steve Fosset oma spetsiaalselt ehitatud lennukis Scaled Composites Model 311 Virgin Atlantic GlobalFlyer? $41467 k m$ . [33ptcg] Tegu oli ebatavalise õhusõidukiga: $83 %$ selle stardikaalust moodustas kütus; lennu jooksul kasutati teepikkuse suurendamiseks hoolikalt ka jugavoole. Oma hapra ehituse tõttu esines sel teekonnal lennukil ka mitmeid tõrkeid.

Selle lihtsa mudeli abil jõuame ka ühe huvitava järelduseni: kui küsime „milline on lendamiseks optimaalne õhutihedus?“ siis leiame, et optimaalsel kiirusel ei sõltu vajatav tõukejõud (C.20) keskkonna tihedusest. Seega oleks meie kujuteldaval lennukil ükskõik, mis kõrgusel see asuks – optimaalset tihedust ei ole olemas. Lennuk saavutaks optimaalse energiakulu (miili galloni kohta) igal kõrgusel, kuid optimaalne kiirus sõltub tihedusest ( $v^{2} \sim \frac{1}{ρ}$ , valem C.16)). Seega, kui kõik muud näitajad on samad, lendaks meie lennuk kõige kiiremini keskkonnas, mille õhutihedus oleks võimalikult madal. Päris mootorite efektiivsused aga sõltuvad nii kiirusest kui ka õhutihedusest. Kuna lennuk muutub kütuse põletamise tagajärjel kergemaks, järeldub meie mudelist, et selle lennuki optimaalne kiirus mingi kindla õhutiheduse korral kahaneks

v^{2} \sim (\frac{m g}{ρ (c_{d} A_{p} A_{s})^{\frac{1}{2}}})

Seega peaks ühtlase õhutihedusega keskkonnas lendav lennuk kergemaks muutumise tagajärjel veidi aeglasemalt liikuma. Kuid ei ole võimalik, et lennuk lendab korraga ühtlase kiirusega ning optimaalse kiirusega, kui see tõuseb õhutiheduse langetamise eesmärgil ülespoole. Järgmine kord pikalt lennates pane tähele, kas piloot tõstab lennu hilisemas faasis lennukit kõrgemale – näiteks $9450$ meetrilt $11890$ meetrini.

Kui efektiivne oleks vesinik-lennuk?

Jõudsime juba järelduseni, et lendamise efektiivsus (ühikutes energia tonn-kilomeetri kohta) on lihtsalt ühe ühikuta numbri ning $g$ korrutis. Kütuse muutmine seda põhimõtet ei muudaks. Vesiniku jõul lendavate lennukite teemal arutlemine peaks toimuma vaid kliimat mõjutavate emissioonide vähendamise kontekstis. Sellistel lennukitel oleks võib-olla ka suurem lennuulatus. Kuid mingit radikaalselt suuremat energiaefektiivsust pole meil mõtet oodata.

Lennukite efektiivsemaks muutmise võimalused

Sarnaselt haneparvele lendamise abil saaks kütuseefektiivsust kuni $10 %$ võrra tõsta (sest parve tõste- ja takistusjõu suhe on suurem kui üksiku lennuki vastav väärtus), kuid see trikk sõltub muidugi sellest, kas kõik haned tahavad täpselt samal ajal täpselt samasse kohta lennata.

Korraga läbitava vahemaa optimeerimine: pika lennuulatusega lennukid (mis on mõeldud näiteks korraga $15000 k m$ läbimiseks) on oma kütuseefektiivsuselt lühimaa lennukitega võrdsed, sest neil on pardal rohkem kütust ning seega vähem kaupa ja reisijaid. Veidi efektiivsem on jagada pikem vahemaa lühikesteks, vahepeatustega reisideks. Ideaalseks ühe lennu vahemaaks on umbes $5000 k m$ , mis tähendaks tavaliste pikamaa-lennuliinide jaoks ühte või kahte tankimispeatust (Green, 2006). Mitmeetapilised pikamaa-lennuliinid oleksid oma kütusekulu poolest umbes $15 %$ efektiivsemad, kuid sellega seostuksid muidugi mõista muud kulud.

Keskkonnasõbralikud lennukid

Aeg-ajalt kirjutatakse inimestest, kes ehitavad keskkonnasõbralikke lennukeid. Jõudsime selles peatükis juba eelnevalt oma mudeli abil aga järelduseni, mille kohaselt on ükskõik millise lennuki transpordikulu ligikaudu

0, 4 kWh/tonn-km

Meie mudelist järeldub, et ainsad viisid, mille abil üks lennuk saaks seda numbrit paremaks muuta, on vähendada õhutakistust (näiteks võiks lennuki tiibades kasutada mingeid uue põlvkonna tolmuimejaid) või muuta lennuki kuju (muutes seda rohkem hõljuki sarnaseks: selle tiivad peaksid kerega võrreldes palju laiemad olemad; või siis võiks kere üldse olemata jätta). Vaatame siis neile viimase aja „keskkonnasõbralike lennukite“ uudistele otsa, et näha, kas mõni neist õhusõidukitest ka tegelikkuses meie $0, 4 kWh/tonn-km$ piirväärtuseni küündib. Kui lennuk kasutab tonn-kilomeetri kohta vähem kui $0, 4 k W h$ , tuleks meil järeldada, et meie mudel ei tööta.

Joonis C.12: Electra F-WMDJ: $11 k W h$ $100$ reisija-kilomeetri kohta.

Puidust ja kangast ehitatud üheistmeline Electra läbis lõunapoolsete Alpide kohal $48$ minuti jooksul $50$ kilomeetrit [6r32hf]. Electra tiivaulatus on $9$ meetrit ning selle $18$ -kilovatist elektrimootorit hoiavad töös $48$ kilogrammi kaaluvad liitium-polümeer akud. Stardihetkel oli õhusõiduki kaaluks $265$ kilogrammi (sellest $134 k g$ moodustas lennuk ise, $47$ kilogrammi kaalusid selle akud ning piloot kaalus $84 k g$ ). 2007. aasta 23ndal detsembril lendas see sõiduk $50$ kilomeetrit. Kui eeldame, et akude energiatihedus oli $130 W h / k g$ ning et selle lennu jooksul kasutati täislaengust ära $90 %$ ( $5, 5 k W h$ ), oli selle lennuki transpordikulu umbkaudu

0, 4 k W h / t o n n - k m

ehk täpselt sama, mida me oma mudeli põhjal ennustasime. See elektriline õhusõiduk pole tavapärasest fossiilkütust neelavast lennukist efektiivsem. See ei tähenda muidugi, et elektrilennukid poleks huvitavad. Kui me suudaksime traditsioonilised lennukid asendada selliste alternatiivsete õhusõidukitega, mille energiakulu oleks sarnane kuid millel puuduksid heitgaasid, oleks tõepoolest tegu kasuliku tehnoloogiaga. Reisijate transpordi aspektist saavutab Electra auväärse tulemuse $111 k W h$ $100$ reisija-kilomeetri kohta – see on meie transpordijoonisel toodud elektriautoga võrreldav suurus. Kuid selles raamatus küsime me alati: „Kust on see energia pärit?“

Ka mitmed veesõidukid on linnud

Veidi pärast selle lendamist kirjeldava mudeli kirjutamist mõistsin, et seda saab rakendada laiemalt kui lihtsalt õhulindudele – see kehtib ka tiiburlaevade ja muude ülikiirete veesõidukite puhul: igas olukorras, milles veesõiduk suurel kiirusel vee kohal hõljub.

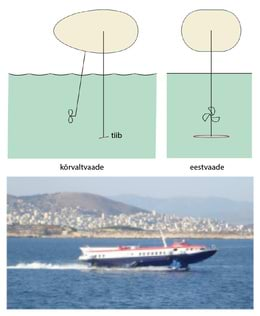
Joonisel C.13 on püütud seletada tiiburlaeva tööpõhimõtet. Sõiduki massi toetab kaldenurga all paiknev veealune tiib, mis tihtipeale on sõidukist endast palju väiksem. See tiib tekitab vett allapoole surudes ülespoole suunatud tõukejõu – täpselt nagu joonisel C.2 kujutatud lennuk. Kui eeldame, et takistusjõust moodustab enamuse just tiivale mõjuv takistusjõud ning et tiiva mõõtmed ning veesõiduki liikumiskiirus on kütusekulu efektiivsuse osas juba optimeeritud, siis on parim saavutatav transpordikulu (tonn-kilomeetri kohta vajaminev energiahulk) täpselt sama nagu leidsime valemist C.26:

(C.34)

\frac{(c_{d} f_{A})^{\frac{1}{2}}}{ε} g

milles $c_{d}$ on veealuse tiiva takistustegur, $f_{A}$ on juba varem defineeritud pindalade suhet kirjeldav ühikuta suurus, $ε$ on mootori efektiivsus ning $g$ on gravitatsioonikiirendus.

Võib-olla pole $c_{d}$ ning $f_{A}$ täpselt samad mis optimeeritud lennukil, kuid selle teooria üks hämmastavaid omadusi on fakt, et see ei sõltu selle keskkonna tihedusest, milles meie sõiduk liigub. Seega on meie transpordikulu umbkaudne hinnang (energiakulu läbitud vahemaa ja kaalu – seehulgas sõiduki enda kaalu – kohta) tiiburlaeva puhul sama mis lennuki puhul! Seega ligikaudu $0, 4 kWh/tonn-km$ .

Selliste sõidukite puhul, mis veepinda vaid aeg-ajalt puudutavad (näiteks katamaraanid ja veesuusad), peaks täpne mudel sisaldama ka lainete tekitamiseks kuluvat energiat. Siiski on mul tunne, et meie tiiburlaeva teooria on vähemasti ligikaudselt täpne.

Seni pole mul õnnestunud tiiburlaevade transpordikulu kusagilt leida, kuid kiirusel $41 k m / h$ liikuva reisijatetranspordiks mõeldud katamaraani andmed paistavad meie ennustusega üpris hästi kooskõlas olevat: sellise sõiduki energiakulu on ligikaudu $1 k W h$ tonn-kilomeetri kohta. Minu jaoks tundub üpriski üllatav, et laeva asemel lennukiga saarelt saarele rändav reisija ei kuluta mitte ainult vähem aega vaid tõenäoliselt ka vähem energiat!

Teisi õhus püsimise viise

Õhulaevad

Joonis C.14: $239$ meetri pikkune USS Akron (ZRS-4) Manhattani kohal lendamas. See kaalus $100$ tonni ning selle kandevõime oli $83$ tonni. Mootorite koguvõimsus oli $3, 4 M W$ , kusjuures kiirusel $93 k m / h$ lennates mahtus selle pardale $89$ meeskonnaliiget ning suurel hulgal relvi. Lisaks kasutati sõidukit ka lennukikandjana.

Selles peatükis rõhutasime, et lennukid ei oleks madalama lennukiiruse korral efektiivsemad, sest väiksemast õhutakistusest põhjustatud võit tasakaalustuks selle lisaenergiaga, mis kuluks õhu tugevamini allasurumiseks. Kas saame selle probleemi ületada, kui muudame oma strateegiat: lõpetame õhu alla surumise ning muutume selle asemel sama kergeks kui õhk? Õhulaev, zeppelin ehk tirižaabel kasutab õhus püsimiseks hiigelsuurt heeliumiga täidetud õhupalli. Heelium on kergem kui õhk, mistõttu aitab see tasakaalustada õhulaeva väikese kabiini massi.

Selle strateegia miinuseks on tõsiasi, et hiigelsuur õhupall suurendab märgatavalt sõidukile mõjuvat õhutakistust.

Õhulaeva energiakulude madalal hoidmiseks (kaalu ja läbitava vahemaa kohta) tuleb sel liikuda aeglaselt, selle kuju peab olema kala-sarnane ning lisaks peab see olema väga suur ning pikk. Proovime koostada mudeli, mis aitaks meil kirjeldada ideaalse õhulaeva energiakulu.

Ma eeldan, et meie õhupall on ellipsoidaalne; olgu selle ristlõikepindala $A$ ning pikkus $L$ . Õhupalli ruumala on seega $V = 2 / 3 A L$ . Kui õhulaev liigub ühtlaselt õhus tihedusega $ρ$ , on sõiduki kogumass (seehulgas nii selle kaup kui ka heelium) $m_{total} = ρ V$ .

Kui meie õhulaev liigub kiirusega $v$ , on õhutakistuse poolt sellele avaldatav jõud

(C.35)

F = \frac{1}{2} c_{d} A ρ v^{2}

milles $c_{d}$ on õhutakistustegur - lennukite andmetele põhinedes on see ligikaudu $0, 03$ . Ühikulise vahemaa läbimiseks kuluv energiahulk on $F$ jagatud mootorite efektiivsusega $ε$ . Seega on kogu transpordikulu ehk ühikulise vahemaa läbimiseks kuluv energiahulk ühikmassi kohta:

(C.35, C.36)

\begin{matrix} \frac{F}{ε m_{total}} & = \frac{\frac{1}{2} c_{d} A ρ v^{2}}{ε ρ \frac{2}{3} A L} = \frac{3}{4 ε} c_{d} \frac{v^{2}}{L} \end{matrix}

Pean ütlema, et see on üpriski kena tulemus! Selle ideaalse õhulaeva transpordikulu sõltub ainult selle kiirusest $v$ ning pikkusest $L$ , kuid mitte õhutihedusest $ρ$ ega õhupalli esipinna pindalast $A$ .

Meie mudel kehtib muutmata kujul ka allveelaevade kohta. Õhulaeva transpordikulu ( $k W h$ tonn-kilomeetri kohta) on sama mis täpselt sama pikal ning sama kiirusega liikuval allveelaeval. Allveelaev aga sisaldab $1000$ korda rohkem massi, sest vesi on õhust $1000$ korda tihedam, ning selle edasiliigutamine on $1000$ korda kulukam. Ainus erinevus nende kahe sõiduki vahel on reklaamikulud.

Hea küll – paneme meie valemisse nüüd ka mõned numbrid sisse. Eeldame, et me soovime liikuda kiirusega $80 k m / h$ (tänu millele kuluks meil Atlandi ookeani ületamiseks kolm päeva). SI ühikutes teeb see $22 m / s$ . Võtame efektiivsuseks $ε = 1 / 4$ . Kui pikk peaks meie õhulaev olema et saavutada parim võimalik transpordikulu? Hindenburg oli $245$ meetrit pikk. Kui võtame $L = 400 m$ , on meie transpordikulu:

\begin{matrix} \frac{F}{ε m_{kogu}} & = 3 \times 0, 03 \frac{22 m / s^{2}}{400 m} = 0, 1 m / s^{2} = 0, 03 k W h / t o n n - k m \end{matrix}

Kui kasulik kaup moodustab meie õhulaeva massist poole, on selle hiiglasliku sõiduki transpordi kogukulu $0, 06 k W h / t o n n - k m$ – see on võrreldav näiteks rongidega.

Laugurid

Laugur ehk ekranoplaan on pinnaefektil töötav veesõiduk: laugur ei püsi õhus mitte tänu õhu ega vee allapoole surumisele vaid kasutab hõljumiseks selle tiibade ning veepinna vahel oleva kokkusurutud õhu „patja.“ Seda pinnaefekti saame näha, kui laseme mängukaardil üle lameda lauapinna liuelda. Selle õhupadja hoidmine nõuab väga vähe energiat, mistõttu on pinnaefektil töötavad veesõidukid oma energiakulu poolest justkui tavasõidukid, millele ei mõju veeretakistust. Lauguri liikumisel kulub suurem osa energiast õhutakistuse ületamisele. Pidagem meeles, et optimaalse kiirusega lendava lennuki puhul kulub pool selle energiast õhutakistuse ületamisele ning pool õhu allapoole surumisele.

Joonis C.16: Laugur nimega Lun – veidi pikem ja raskem kui Boeing 747.

Ekranoplaan töötati välja Nõukogude Liidus Hrustšovi ajal sõjaväe transpordivahendina ning raketiheitjana. Ekranoplaan Lun lendas kiirusega $500 k m / h$ ning selle kaheksa mootori kogutõukejõud oli $1000 k N$ – pärast veepinna kohale kerkimist kulus sel aga palju vähem energiat. Kui eeldame, et lennu ajal oli vajalik tõukejõud vaid veerand maksimumist, et mootorite efektiivsus oli $30 %$ ning et selle $400$ -tonnisest massist moodustas transporditav kaup $100$ tonni, oli selle sõiduki kogu transpordikulu $2 k W h$ tonn-kilomeetri kohta. Kujutan ette, et mittesõjaväelises kasutuses oleva transpordivahendina moodustaks ekranoplaani transpordikulu umbes pool tavalise lennuki transpordikulust.

Müütarusaamad

Lennuk lendas ju nagunii – seega oli minu reis energianeutraalne.

See väide on vale kahel põhjusel. Esiteks nõuab sinu tõttu lisanduv mass lennukilt lisaenergia kasutamist. Teiseks vastavad lennufirmad nõudluse kasvule väljumiste lisamisega.

Märkused ja edasine lugemine

Boeing 747. 747 õhutakistustegur: www.aerospaceweb.org. Ülejäänud 747 andmed [2af5gw]. Albatrossi andmed [32judd].

Tegelike reaktiivmootorite efektiivsus on ligikaudu $ε = 1 / 3$ . Tavalise mootori energiaefektiivsus jääb vahemikku $23 %$ - $36 %$ [adg.stanford.edu/aa241/p]. Tavalise lennuki puhul jääb mootorite efektiivsus kusagile $20$ ja $40$ protsendi vahele, kusjuures parimad turboventilaatormootorid saavutavad optimaalsel lennukõrgusel $30$ – $37$ protsendilise efektiivsuse [www.grida.no/climate/ipcc/aviation/097.htm]. Siinkohal pole aga lahenduseks lihtsalt kõige efektiivsema mootori valimine, sest see võib kaaluda palju rohkem (st selle mass avaldatava tõukejõu kohta on suurem), mistõttu kannatab kogu lennuki üleüldine efektiivsus.

Pikim mõõdetud linnu lennuulatus...

New Scientist 2492. “Vöötsaba-vigle on taeva valitseja.” 26 märts, 2005. 11 September, 2007: Vigle lendas peatusteta $11500 k m$ Alaskast Uus-Meremaale. [2qbquv]

Korraga läbitava vahemaa optimeerimine: ideaalseks ühe lennu vahemaaks on umbes $5000 k m$ . Allikas: Green (2006).

Reisijatetranspordiks kasutatava katamaraani andmed. Allikas: [5h6xph]. Veeväljasurve (täiskoormaga): $26, 3$ tonni. $1050$ meremiili pikkusel reisil tarbis see vaid $4780$ liitrit kütust. Minu arvutuste kohaselt teeb see transpordikuluks $0, 93 k W h$ tonn-kilomeetri kohta. Siinkohal arvestasin ma muide sõiduki kogumassi. Sama sõiduki transpordiefektiivsus reisija kohta on ligikaudu $35 k W h$ $100$ reisija-kilomeetri kohta.

Ekranoplaan Lun. Allikad: www.fas.org, (Taylor, 2002a).

Edasine lugemine: Tennekes (1997), Shyy et al. (1999).