Kõik aatomitest

Füüsiku pilguga

Peagi pärast laserite leiutamist 1960ndatel aastatel võeti need uurimislaboreis kasutusele uudsete valgusallikatena. Tänapäeval on laserid üldlevinud paljudes valdkondades, nagu näiteks salvestustehnikas ja andmesides, maamõõtmises, keevitamises, vöötkoodi lugemises kassaautomaatides jne. Fotol valmistatakse patsienti ette laser-silmaoperatsiooniks: selle naise silma sarvkesta töödeldakse ultravioletse laserkiirega, et korrigeerida tema nägemisteravust. Nii laseri kui ka kõikide teiste valgusallikate valgust kiiratakse aatomitest. Mis siis on laserivalguses nii erilist?

JOONIS 40-1 Sinine täpp on baariumi üksikaatomi kiiratud valguse fotojäädvustus. Aatomit hoiti Washingtoni ülikoolis kestvalt püünises. Seda sunniti korduvalt kiirgama siirdel ühe ja sama energiatasemete paari vahel. Täpp on kujunenud paljude footonite kuhjumisest. (Foto avaldatud Warren Nagourney loal)

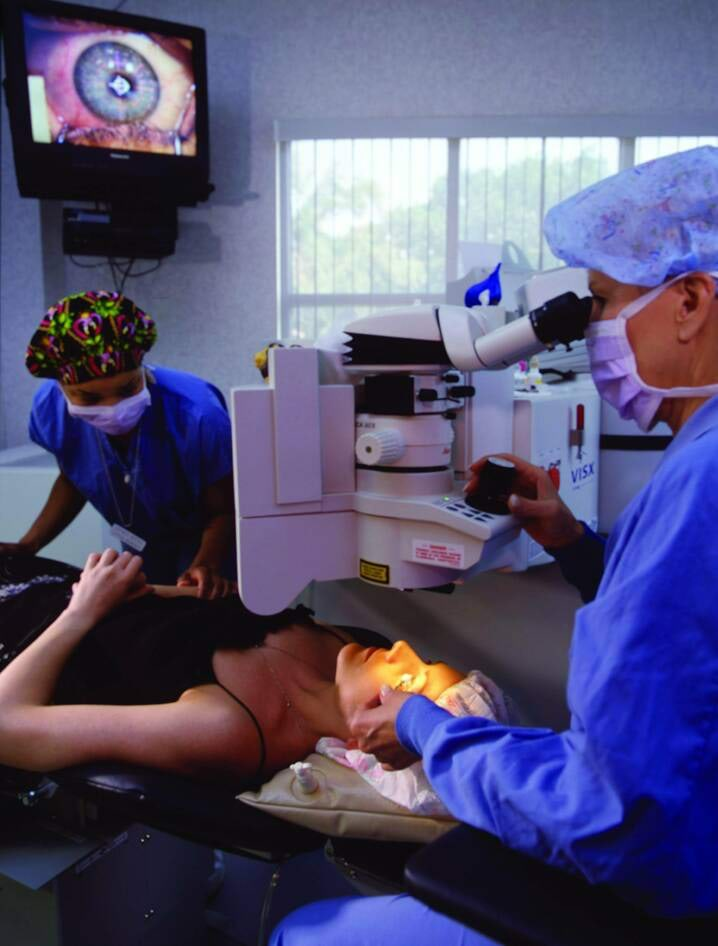
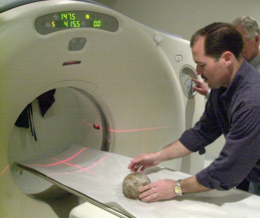
Selles peatükis jätkame juttu sellest, kuidas jõuti füüsika ühe põhieesmärgini: aatomite olemasolu ja omaduste väljaselgitamiseni. Umbes sada aastat tagasi ponnistasid füüsikud jõudu, et leida katset, mis vaieldamatult tõestaks aatomite olemasolu. Tänapäeval ei kahtle keegi selles, et aatomid olemas on. Tunnelmikroskoobis me lausa näeme üksikaatomeid. Võime neid nihutada mööda pindu, näiteks selleks, et moodustada kvantkopleid, nagu 39. peatüki avafotol kujutatud. On kogunisti võimalik hoida üksikaatomit kuitahes kaua püünises (joonis 40-1), et uurida teistest täielikult isoleeritud aatomi omadusi.

Aatomi mõningatest omadustest

Võidakse arvata, et aatomifüüsika on argielust üpris kaugel. Kummatigi, kas olete mõelnud, kuidas meid mõjutavad aatomite järgmised omadused?

Aatomite püsikindlus. Valdav osa aatomeid, mis moodustavad meie maailma, on eksisteerinud muutumatult miljardeid aastaid. Maailm oleks ju lausa pöörane, kui aatomid alatasa teistsugusteks muutuksid.

Aatomid ühinevad üksteisega. Need „kleepuvad” kokku molekulideks ja kuhjuvad tahkisteks. Suurem osa igast aatomist on tühi ruum, kuid ometi võime julgesti seista aatomeist moodustunud põrandal ega kuku sellest läbi.

Kvantfüüsika annab seletuse nii nendele kui ka aatomite järgmistele omadustele.

Aatomite ehituses ilmneb süsteem

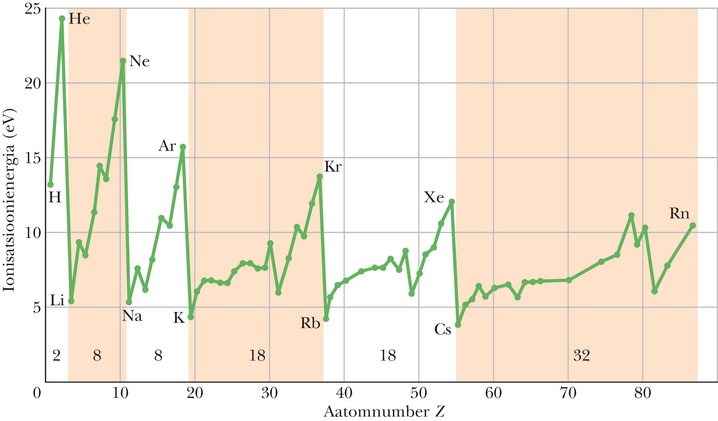
Joonisel 40-2 on näide aatomite omaduste korduvusest nende perioodilisussüsteemis (Lisa G). Graafikul on elementide ionisatsioonienergia sõltuvus nende aatomnumbrist ehk teisisõnu elemendi asendist perioodilisussüsteemis. Ionisatsioonienergia on minimaalne energia, mis kulub kõige nõrgemini seotud elektroni eemaldamiseks aatomist. Elementide keemiliste ja füüsikaliste omaduste silmatorkav sarnasus perioodsustabeli igas püsttulbas näitab veenvalt, et aatomid koostuvad reeglipäraselt.

JOONIS 40-2 Elementide ionisatsioonienergiate sõltuvus nende aatomnumbrist. Joonis näitab omaduste korduvust elementide perioodilisustabeli kuues täielikult täidetud horisontaalses perioodis. Alaservas on märgitud elementide arv igas perioodis.

Perioodilisussüsteemis on elemendid järjestatud kuude täielikku horisontaalsesse perioodi (seitsmes periood ei ole täielik). Kui esimene periood välja arvata, siis algab igaüks neist vasakul ägeda reaktsioonivõimega leelismetalliga (liitium, naatrium, kaalium jne) ja lõpeb paremal inertse väärisgaasiga (neoon, argoon, krüptoon jne). Kvantfüüsika annab seletuse nende elementide omadustele. Elementide arv kuues perioodis on järgmine:

2, 8, 8, 18, 18 ja 32

Ka need arvud johtuvad kvantfüüsikast.

Aatomid kiirgavad ja neelavad valgust

Veendusime juba, et aatomid võivad olla üksnes diskreetsetes kvantolekutes, milledest igaühel on kindel energia. Aatom võib siirduda ühest olekust teise, kiirates (hüpates madalamale tasemele $E_{madalam}$ ) või neelates valgust (hüpates kõrgemale tasemele $E_{k ˜ o rgem}$ ). Punktis 39-3 selgitati, et valgust kiiratakse või neelatakse footonina, mille energia on

(40-1)

h f = E_{k ˜ o rgem} - E_{madalam}

Seega taandub aatomi poolt kiiratava või neelatava valguse sageduse leidmine aatomite kvantseisundite energia arvutamisele; seda võimaldab kvantfüüsika, vähemalt põhimõtteliselt.

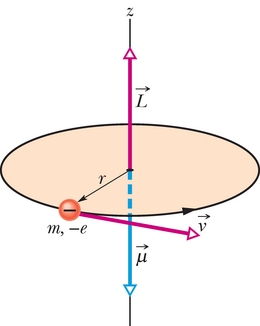
Aatomitel on impulsimoment ja magnetomadused

JOONIS 40-3 Klassikaline mudel: osake massiga $m$ ja laenguga $- e$ tiirleb kiirusega $v$ ringjoonel raadiusega $r$ . Osakesel on impulsimoment $\to L = \to r \times \to p$ , kus $\to p$ on impulss $m \to v$ . Osakese liikumine on võrdväärne vooluringiga, mille magnetmoment $\to μ$ on vastassuunaline vektorile $\to L$ .

Joonisel 40-3 on negatiivse laenguga osake, mis tiirleb ringorbiidil paigaloleva keskme ümber. Nagu selgus punktis 32-7, on orbiidil tiirleval osakesel nii impulsimoment $\to L$ kui ka magnetiline dipoolmoment $\to μ$ . (Viimane seepärast, et selle trajektoor on ekvivalentne miniatuurse vooluringiga). Joonis 40-3 näitab, et mõlemad vektorid $\to L$ ja $\to μ$ on risti orbiidi tasandiga, kuid, kuna laeng on negatiivne, siis on need vastassuunalised. Joonis 40-3 kujutab klassikalist mudelit, seepärast ei esita see elektroni aatomis õigesti. Kvantfüüsikas tuleb elektron asendada tõenäosustiheduse mudeliga, mida kõige paremini näitlikustab täpp-pilt. Kuid ka kvantfüüsikas kehtib tõik, et elektroni igal kvantseisundil on (üldiselt) impulsimoment ja sellele vastassuunaline magnetdipoolmoment (öeldakse, et need on seostatud suurused).

Einsteini ja de Haasi katse

Aastal 1916 sooritasid Albert Einstein ja Hollandi füüsik W.J. de Haas ühiselt nutika katse näitamaks, et üksikaatomite impulsimoment ja magnetmoment on omavahel seotud.

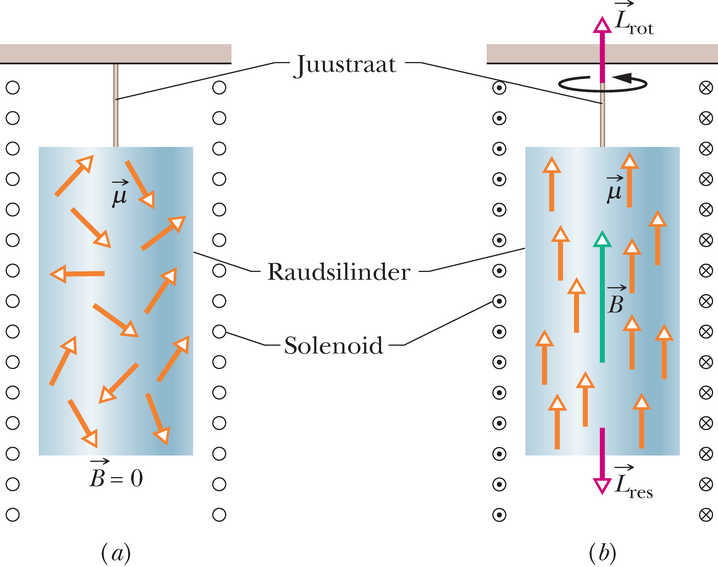
Katse skeem on toodud joonisel 40-4. Nad riputasid raudsilindri peene traadi otsa ja paigutasid selle siis solenoidi. Kui solenoidis puudub vool, on aatomite magnetmomendid kaootilised, kindla suunata, ning tühistavad üksteist vastastikku (joonis 40-4a). Niipea kui solenoidi lülitatakse vool, mis tekitab solenoidi telje suunas magnetvälja $\to B$ , pöörduvad aatomite magnetmomendid välja suunaga paralleelseks. Ühtlasi peavad siis pöörduma ka magnetmomendiga seostatud impulsimomendid ${\to L}_{r e s}$ .

JOONIS 40-4 Einsteini ja de Haasi katseseade. (a) Algselt puudub raudsilindris magnetväli, aatomite magnetdipoolmomendid $\to μ$ (nagu ka impulsimomendid) on orienteeritud kaootiliselt. (b) Kui solenoidi lastakse vool, mis tekitab pooli telje suunas magnetvälja, pöörduvad magnetmomendid $\to μ$ välja $\to B$ suunas, impulsimomendid vastassuunas. Kuna silindrile ei mõju algselt välisjõude, peab selle impulsimoment (pöörlemishulk) säilima ja see pöördub tervikuna nii nagu joonisel näidatud.

Silindrile ei mõju mingit välist jõumomenti, seepärast peaks selle impulsimoment jäämagi nulliks. Kuid aatomite impulsimomente $\to L$ suunav magnetväli tekitab silindrile mõjuva makroskoopilise momendi ${\to L}_{r o t}$ (joonis 40-4b). Et säilitada impulsimomenti (mis alguses oli null), siis pöördub silinder ümber oma telje, et tekitada vastassuunalist momenti.

Kui silinder ei ripuks elastse juustraadi otsas, jääkski see pöörlema seniks, kuni magnetväli mõjub. Kuid traadi vääne tekitab vastassuunalise momendi, mis peagi silindri peatab ja seda vastassuunas pöörama hakkab, seni kui vääne kaob. Sedasi hakkab silinder telje ümber harmooniliselt võnkuma. (Võnkumisi hoitakse solenoidi vahelduvvoolu suunates.) Silindri pöördvõnkumine tehakse nähtavaks traadi külge kinnitatud peeglilt peegelduva valguskiire suunamuutuse kaudu.

See katse näitas ilmekalt, et aatomite kvantseisunditega seotud impulsimomendid on makroskoopilise objekti pöörde järgi lausa silmaga vaadeldavad.

Elektroni spinn

Punktis 32-7 seletati, et elektronil on alati siseomane spinnimpulsimoment ehk lihtsalt spinn $\to S$ . See on elektroni püsiomadus, sama moodi kui mass ja elektrilaeng. Järgmises punktis näitame, et spinn on kvanditud, s.t määratud spinnkvantarvuga $s$ , mis on elektronidel, prootonitel ja neutronitel alati $\frac{1}{2}$ . Lisaks on kvanditud ka spinni $\to S$ komponent piki suvalist telge. See sõltub spinni magnetkvantarvust $m_{s}$ , mis omandab üksnes väärtusi $+ \frac{1}{2}$ ja $- \frac{1}{2}$ .

Elektroni spinni olemasolu postuleerisid katsele tuginedes kaks Hollandi doktoranti, George Uhlenbeck ja Samuel Goudsmit. Teoreetiliselt tõi spinni sisse Inglise füüsik P.A.M. Dirac, kes rajas 1929. aastal elektroni relativistliku kvantteooria.

Tihti tekib kiusatus tõlgendada elektroni spinni käsitades elektroni kerakesena, mis pöörleb ümber oma telje (sellest nimetuski: ingl to spin – ketrama, pöörlema). Kuid see klassikaline mudel, niisamuti kui orbiitide mudelgi, pole pädev. Õigem on pidada spinni elektroni mõõdetavaks siseomaduseks. Seda ei saa näitlikustada.

Punktis 39-9 tõime välja kvantarvud, mis tulevad esile Schrödingeri võrrandi rakendamisel vesiniku aatomile (tabel 39-2). Nüüd võime kvantarvude tabelit laiendada, võttes hulka ka arvud $s$ ja $m_{s}$ (tabel 40-1). Viie kvantarvu komplekt iseloomustab täielikult elektroni kvantseisundit vesiniku aatomis või mistahes teiseski aatomis. Kõik seisundid, millel on ühine kvantarv $n$ , moodustavad
elektronkihi. Loendades $ℓ$ ja $m_{ℓ}$ väärtusi ja siis korrutades selle tulemuse kahega, et arvestada ms kaht lubatud väärtust, leiame, et elektronkiht sisaldab $2 n^{2}$ seisundit. Kõik seisundid ühesuguse $n$ ja $ℓ$ väärtusega moodustavad alamkihi. Selles on kõikidel elektronidel üks ja sama energia. Võite rehkendada, et alamkiht, mida iseloomustab kvantarv $ℓ$ , sisaldab $2 (2 ℓ + 1)$ olekut.

Impulsimomendid ja magnetilised dipoolmomendid

Aatomi iga kvantseisundiga on seotud orbitaalne impulsimoment ning temale vastav magnetiline dipoolmoment. Igal elektronil, ükskõik kas aatomisse lõksustatul või vabal, on spinnmoment ja temaga seotud magnetmoment. Käsitleme neid suurusi esiteks ühekaupa, siis kõiki koos.

Orbitaalne impulsimoment ja magnetism

Orbitaalse impulsimomendi $\to L$ suurus $L$ on aatomis kvanditud, s.t see omandab vaid väärtusi

(40-2)

L = \sqrt{ℓ (ℓ + 1)} ℏ

kus $ℓ$ on orbitaalkvantarv ja $ℏ$ tähistab suurust $h / 2 π$ . Tabelist 40-1 on näha, et $ℓ$ on kas null või positiivne täisarv, väiksem kui $n - 1$ . Näiteks kui $n = 3$ , siis on $ℓ$ lubatud väärtused $2, 1$ ja $0$ .

Punktis 32-7 nägime, et magnetiline dipool on seotud aatomis oleva elektroni orbitaalse impulsimomendiga $\to L$ . Magnetdipoolil on orbitaalne magnetiline dipoolmoment ${\to μ}_{o r b}$ , mis on seotud impulsimomendiga seose 32-28 kaudu:

(40-3)

{\to μ}_{o r b} = - \frac{e}{2 m} \to L

Miinusmärk on valemis seepärast, et ${\to μ}_{o r b}$ ja $\to L$ on vastassuunalised. Kuna $\to L$ on kvanditud, peab ka ${\to μ}_{o r b}$ olema kvanditud:

(40-4)

{\to μ}_{o r b} = \frac{e}{2 m} \sqrt{ℓ (ℓ + 1)} ℏ

Ei ${\to μ}_{o r b}$ ega ka $\to L$ ole mõõdetavad. Mõõdetavad on üksnes nende kahe vektori komponendid mistahes suunas. Kujutleme, et aatom asub magnetväljas $\to B$ ; eeldame, et
$z$ -telg on suunatud piki magnetvälja jõujooni kohas, kus aatom asub. Siis saame mõõta nii ${\to μ}_{o r b}$ kui ka $\to L$ $z$ -komponente.

Orbitaalse magnetilise dipoolmomendi komponendid $m_{o r b, z}$ on kvanditud ning avalduvad kujul:

(40-5)

m_{o r b, z} = - m_{ℓ} μ_{B}

Siin on $m_{ℓ}$ magnetkvantarv (vt tabel 40-1) ja $μ_{B}$ on Bohri magneton:

(Bohri magneton, 40-6)

μ_{B} = \frac{e h}{4 π m} = \frac{e ℏ}{2 m} = 9, 274 \times 10^{- 24} J / T

Joonis 40-5 Seisundis $ℓ = 2$ oleva elektroni $L_{z}$ lubatud väärtused. Igale orbitaalse impulsimomendi vektorile $\to L$ vastab vastassuunaline orbitaalse magnetilise dipoolmomendi vektor ${\to μ}_{o r b}$ .

kus $m$ on elektroni mass.

Impulsimomendi $z$ -komponendid on samuti kvanditud ja avalduvad järgnevalt:

(40-7)

L_{z} = m_{ℓ} ℏ

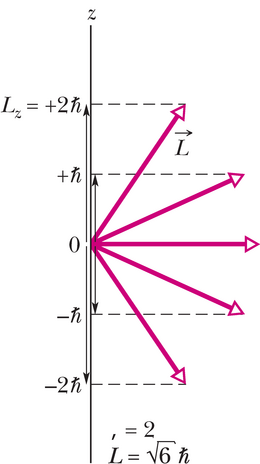
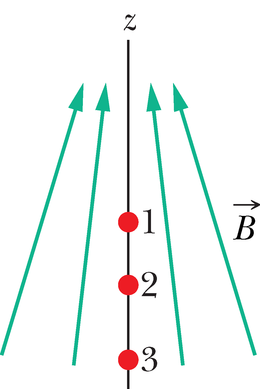
Joonisel 40-5 on näidatud viis orbitaalmomendi kvanditud komponenti $L_{z}$ elektronil, mille $ℓ = 2$ . Ühtlasi on toodud ka impulsimomendi $\to L$ orientatsioonid. Kuid joonist ei maksa ülearu usaldada, sest $\to L$ pole mingil moel määratav. Seepärast võib joonist käsitada üksnes kui visuaalset abivahendit. Võime kokkuleppeliselt öelda, et $\to L$ asetub $z$ -telje suhtes teatava nurga $θ$ all, mis rahuldab seost

(40-8)

cos θ = \frac{L_{z}}{L}

Nurka $θ$ võiksime nimetada poolklassikaliseks nurgaks vektori $\to L$ ja $z$ -telje vahel, sest $θ$ on millegi sellise klassikaline mõõt, mis kvantteooria järgi mõõdetav pole.

Spinnimpulsimoment ja magnetiline spinndipoolmoment

Spinnimpulsimomendi $\to S$ suurusel $S$ saab nii vaba kui ka sulustatud elektroni korral olla vaid üks kindel väärtus:

(40-9)

S = \sqrt{s (s + 1)} ℏ = \sqrt{(\frac{1}{2}) (\frac{1}{2} + 1)} ℏ = 0, 886 ℏ

Siin on $s$ ( $= \frac{1}{2}$ ) elektroni spinnkvantarv ehk spinn.

Nagu märgitud punktis 32-7, on elektronil siseomane magnetiline spinndipoolmoment, mis on seotud selle sisemise spinnimpulsimomendiga (spinnpöörlemishulgaga) avaldise 32-22 kaudu:

(40-10)

{\to μ}_{s} = - \frac{e}{m} \to S

Miinusmärk tuleneb vektorite ${\to μ}_{s}$ ja $\to S$ vastassuunalisusest. Kuna $\to S$ on kvanditud (vt valem 40-9), peab ka ${\to μ}_{s}$ olema kvanditud:

(40-11)

μ_{s} = \frac{e}{m} \sqrt{s (s + 1)} ℏ

JOONIS 40-6 Komponentide $S_{z}$ , $m_{z}$ lubatud väärtused elektroni korral.

Ei $\to S$ ega ${\to μ}_{s}$ pole otseselt mõõdetavad. Kuid mõõta saab nende komponente mistahes telge pidi. Kui võtame teljeks $z$ -telje, siis

(40-12)

S_{z} = m_{s} ℏ

kus $m_{s}$ on spinni magnetkvantarv (vt tabel 40-1), millel saab olla vaid kaks väärtust: $m_{s} = + \frac{1}{2}$ (tinglikult öeldakse „spinn üles”) ja $m_{s} = - \frac{1}{2}$ („spinn alla”).

Kvanditud on ka magnetilise spinndipoolmomendi komponendid $m_{s, z}$ :

(40-13)

μ_{s, z} = - 2 m_{s} μ_{B}

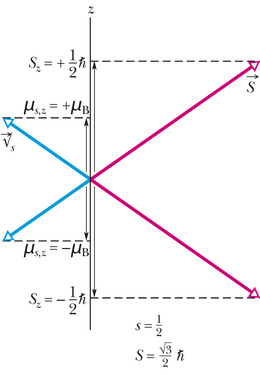
Joonisel 40-6 on kujutatud spinnimpulsimomendi kaks kvanditud komponenti $S_{z}$ ning vektori $\to S$ vastavad orientatsioonid. Jooniselt on näha ka magnetilise spinndipoolmomendi ${\to μ}_{s}$ komponendid $μ_{s, z}$ .

Orbitaalse ja spinnimpulsimomendi liitumine

Aatomile, milles on üle ühe elektroni, saab defineerida summaarse impulsimomendi $\to J$ . See on üksikelektronide orbitaal- ja spinnimpulsimomentide vektorsumma. Elemendi koha perioodilisussüsteemis määrab prootonite arv selle tuumas: aatomnumber ehk laenguarv $Z$ . Kuna neutraalses aatomis on prootonitega võrdne arv elektrone, siis kasutame laenguarvu $Z$ elektronide impulsimomentide summeerimisel ja määratleme $\to J$ järgmiselt:

(40-14)

\to J = ({\to L}_{1} + {\to L}_{2} + {\to L}_{3} + \dots + {\to L}_{Z}) + ({\to S}_{1} + {\to S}_{2} + {\to S}_{3} + \dots + {\to S}_{Z})

JOONIS 40-7 Klassikaline mudel: summaarne impulsimomendi vektor $\to J$ ja efektiivse magnetmomendi vektor ${\to μ}_{e f}$ .

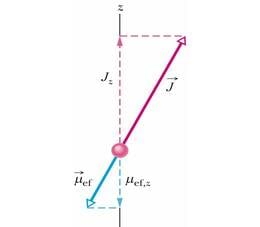
Niisamuti on paljude elektronidega aatomi magnetiline dipoolmoment selle üksikelektronide orbitaalsete magnetiliste dipoolmomentide ja magnetiliste spinndipoolmomentide vektorsumma. Kuid kuna valemis 40-13 (erinevalt valemist 40-5) esineb tegur $2$ , siis ei ühti summaarse magnetilise dipoolmomendi suund vektori $- \to J$ suunaga, vaid moodustab sellega teatava nurga. Seepärast määratletakse aatomi efektiivne magnetiline dipoolmoment $μ_{e f}$ kui üksikute magnetdipoolmomentide vektorsumma komponent $- \to J$ sihis (joonis 40-7). Tavaliselt on aatomis enamiku elektronide orbitaal- ja spinnimpulsimomentide vektorsumma null. Siis annavad $\to J$ ja $μ_{e f}$ summasse panuse vaid suhteliselt väike arv elektrone, tihti üksainus valentselektron.

Elektron on kvantseisundis, milles selle orbitaalse impulsimomendi

\to L

absoluutväärtus on

2 \sqrt{3} ℏ

. Mitu elektroni orbitaalse magnetdipoolmomendi projektsiooni

z

-teljele on võimalikud?

Sterni ja Gerlachi katse

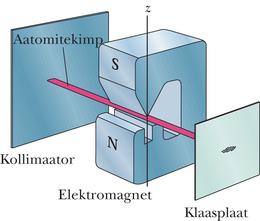
Aastal 1922 näitasid Otto Stern ja Walter Gerlach Hamburgi Ülikoolis katseliselt, et hõbeda aatomite magnetmoment on kvanditud. Katses aurustati hõbe elektriahjus. Ahju seinas oli kitsas pilu, mille kaudu osa auru aatomeid pääses õhutühja torusse. Et aatomitekimpu kitsendada, oli selle teel veel teinegi pilu, kollimaator (joonis 40-8). Kimp juhiti elektromagneti pooluste vahelt läbi ja seejärel sadestus hõbe klaasplaadile.

Kui elektromagnet on sisse lülitamata, sadestub hõbe väikese täpina. Arvutused näitavad, et elektromagneti sisselülitamisel peaks hõbe sadestuma püsttriibuna, sest hõbeda aatomid on magnetdipoolid ja magnetjõud suunavad neid, hälvitades neid veidi üles või alla. Hõbedalaiku analüüsides saab määrata, kui palju aatomid magnetväljas hälbisid. Seejuures tabas Sterni ja Gerlachi üllatus. Enne selle üllatuse ja selle kvantfüüsikaliste järelduste kirjeldust vaatame lähemalt, milline hälvitusjõud aatomitele magnetväljas mõjub.

Hõbeda aatomitele mõjuv hälvitusjõud

Sterni ja Gerlachi katses ei mõju liikuvale osakesele tavapärane hälvitusjõud, mida kirjeldab valem 28-2 ( $\to F = q \to v \times \to B$ ), sest aatomid on neutraalsed, $q = 0$ . Neile rakendub vastastikmõju magnetvälja $\to B$ ja hõbeda aatomi magnetdipooli vahel. Selle saab arvutada dipooli potentsiaalsest energiast $U$ magnetväljas (valem 28-38):

(40-15)

U = - μ \cdot \to B

kus $\to μ$ on aatomi magnetiline dipoolmoment. Joonisel 40-8 on $z$ -telg ja väli $\to B$ suunatud üles. Siis saab valemi 40-15 väljendada aatomi dipoolmomendi projektsiooni $μ_{z}$ kaudu välja $\to B$ suunale:

(40-16)

U = - μ_{z} B

Kasutame valemit 8-22 ( $F = - d U / d x$ ) jõu $z$ -komponendi leidmiseks:

(40-17)

F_{z} = - \frac{d U}{d z} = μ_{z} \frac{d B}{d z}

Seda magnetjõudu, mis hälvitab aatomit magnetvälja läbimisel, me otsimegi.

Tuletis $d B / d z$ on välja gradient piki $z$ -telge. Kui see gradient on null (näiteks homogeenses väljas), siis aatomeid välja läbimisel ei hälvitata. Kirjeldatud katses olid magnetpoolused töödeldud nii, et välja gradient oleks maksimaalne ja aatomite nihe klaasplaadil tuleks selgelt ilmsiks.

Klassikalise füüsika järgi peaks joonisel 40-8 kujutatud magnetvälja läbivate hõbeda aatomite $μ_{z}$ muutuma väärtusest $- μ$ (kui dipoolmoment $\to μ$ on suunatud piki $z$ -telge otse alla) kuni väärtuseni $+ μ$ ( $\to μ$ on suunatud piki $z$ -telge otse üles). Niisiis peaks valemi 40-17 kohaselt aatomitele mõjuv jõud ja seega ka nende hälve lihtsalt muutuma suurimast allapoole suunatust kuni suurima ülespoole suunatuni ja aatomid peaksid sadestuma klaasile piki püstjoont. Aga nii ei juhtu.

Üllatav katsetulemus

Stern ja Gerlach leidsid, et hõbe sadestus klaasplaadile kahe selgelt eraldunud laiguna, üks ülalpool seda kohta, kuhu aatomid pidanuks langema ilma hälvitamata, ja teine tollest hälvitamata kohast niisama kaugel allpool. Õblukesed hõbedalaigud polnud algul nähtavadki ja katsetulemuse ilmutas õnnelik juhus. Nimelt suitsetas Stern odavat sigarit ja kui ta juhtus hingama plaadile, ühines sigarisuitsus leiduv väävel hõbedaga mustaks hõbesulfiidiks, mis oli hästi nähtav.

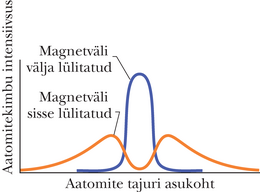
JOONIS 40-9 Sterni ja Gerlachi täiustatud katse tulemus. Kui elektromagnet on välja lülitatud, ilmneb ainult üks aatomite kimp. Kui magnet lülitatakse sisse, lahkneb kimp kaheks. Need vastavad tseesiumi aatomite magnetmomentide orientatsioonile välja suunas ja sellele vastu.

Joonisel 40-9 on hiljem täiuslikuma aparaadiga saadud graafikud. Kasutati tseesiumi aatomeid, mis on samuti magnetdipoolid, ja magnetvälja suurt gradienti $d B / d z$ . Magnetvälja sai lülitada sisse ja välja ning aatomitekimbus nihutati ülesalla tundlikku aatomite detektorit, mille signaalid ongi joonisel kuvatud.

Kui magnetväli oli välja lülitatud, siis aatomid muidugi ei hälbinud ja detektor registreeris üheainsa laigu nagu näidatud joonisel 40-9. Kui väli oli sisse lülitatud, siis lahknes algne kimp kaheks väiksemaks kimbuks, üks ülalpool ja teine allpool esialgset kimpu. Kui detektorit nihutati vertikaalselt läbi nende kimpude, siis registreeris see kaks eraldiasuvat laiku nagu näidatud joonisel 40-9.

Mida need katsetulemused tähendavad

Sterni ja Gerlachi originaalkatses tekkis klaasplaadile kaks hõbedalaiku mitte vertikaalne hõbejälg. Sellest järeldub, et vastupidi klassikalise füüsika ennustusele ei saa magnetmomendi komponendil $μ_{z}$ piki $\to B$ -vektori (ühtlasi $z$ -telje) suunda olla mistahes väärtust $- μ$ ja $+ μ$ vahemikust. Võimalikud on ainult kaks väärtust, milledest kumbki vastab ühele laigule klaasil. Seega on $μ_{z}$ (siis ka $\to μ$ ) kvanditud. Kuna aatomi impulsimoment $\to L$ on magnetmomendiga $\to μ$ seotud, peab seegi ja selle komponent $L_{z}$ olema kvanditud.

Kaasaegsest kvantteooriast teame, et paljuelektronilises hõbeda aatomis on igal elektronil nii orbitaalne kui ka spinnmagnetmoment. Teame ka, et need vektorid summeeruvad nulliks, kui välja arvata üks elektron, mille orbitaalne dipoolmoment on null. Järelikult moodustab aatomi summmaarse magnetmomendi $\to μ$ üksnes tolle ühe elektroni spinnmoment. Valemi 40-13 järgi saab projektsioonil $μ_{z}$ piki $z$ -telge joonisel 40-8 olla ainult kaks väärtust: üks kvantarvuga $μ_{s} = + \frac{1}{2}$ („spinn üles”), teine $μ_{s} = - \frac{1}{2}$ („spinn alla”). Asendus avaldisse 40-13 annab

(40-18)

μ_{s, z} = - 2 (+ \frac{1}{2}) μ_{B} = - μ_{B} ja μ_{s, z} = - 2 (- \frac{1}{2}) μ_{B} = + μ_{B}

Edasi, asendades need $μ_{z}$ valemisse 40-17, leiame, et aatomeid magnetväljas hälvitava
jõu komponendil $F_{z}$ saab olla üksnes kaks väärtust:

(40-19)

F_{z} = - μ_{B} (\frac{d B}{d z}) ja F_{z} = + μ_{B} (\frac{d B}{d z})

Seepärast tekibki klaasile kaks hõbedalaiku.

Sterni ja Gerlachi katses (joonis 40-8) läbib hõbeda aatomite kimp

z

-telje suunalise magnetvälja gradiendi

d B / d z = 1, 4 T / m m

. Gradiendiala pikkus w algkimbu suunas on

3, 5 c m

. Aatomite kiirus on

750 m / s

. Millisele kaugusele

d

on aatomid hälvitatud, kui need gradiendi piirkonnast väljuvad? Hõbeda aatomi mass on

1, 8 \times 10^{- 25} k g

.

Lahendus

JUHTMÕTTED (1) Hälvituse tingib aatomi magnetdipooli ja magnetvälja vastastikmõju gradiendi tõttu. Hälvitusjõud (valem 40-19) mõjub gradiendi ( $z$ -telje) suunas. Arvutame üksnes hälbe $z$ -telje positiivses suunas, s.t on tarvis teada $F_{z} = μ_{B} (d B / d z)$ . (2) Eeldame, et välja gradient on ühesugune kogu piirkonnas, mida hõbeda aatomid läbivad. Siis on jõud $F_{z}$ ja Newtoni teise seaduse järgi ka aatomi kiirendus seal konstantne.

Arvutused: öeldust lähtudes saame kiirenduseks

a_{z} = \frac{F_{z}}{M} = \frac{μ_{B} (d B / d z)}{M}

Et kiirendus on konstantne, võime kasutada valemit 2-15 tabelist 2-1, et arvutada $z$ -telje suunaline hälve $d$ :

d = v_{0 z} t + \frac{1}{2} a_{z} t = 0 t + \frac{1}{2} (\frac{μ_{B} (d B / d z)}{M}) t^{2}

Kuna hälvitusjõud mõjub aatomile risti selle esialgse liikumissuunaga, siis aatomi algkiiruse komponent algses liikumissuunas $v$ ei muutu. Aatom vajab aega $t = w / v$ , et läbida teepikkust $w$ selles suunas. Asendame valemis 40-2 aja $t$ avaldisega $w / v$ , leiame

d = \frac{1}{2} (\frac{μ_{B} (d B / d z)}{M}) {(\frac{w}{v})}^{2} = \frac{μ_{B} (d B / d z) w^{2}}{2 M v^{2}} = (9, 27 \times 10^{- 24} J / T) (1, 4 \times 10^{3} T / m) \times \frac{(3, 5 \times 10^{- 2} m)^{2}}{(2) (1, 8 \times 10^{- 25} k g) (750 m / s)^{2}} = 7, 85 \times 10^{- 5} m \approx 0, 08 m m - -------- - - -------- -

Kahe lahknenud kiire nihe on sellest kaks korda suurem: $0, 16 m m$ . Vahe on pisike, kuid mõõdetav.

Magnetresonants

JOONIS 40-10 Prootoni magnetilise spinndipoolmomendi vektori $\to μ$ $z$ -komponent (a) väiksema energiaga $↑$ ja (b) suurema energiaga $↓$ seisundis. (c) Seisundite energiatasemete diagramm, millel on märgitud kvanthüpe, mille prooton sooritab, kui selle spinn teeb pööraku seisundist $↑$ seisundisse $↓$ .

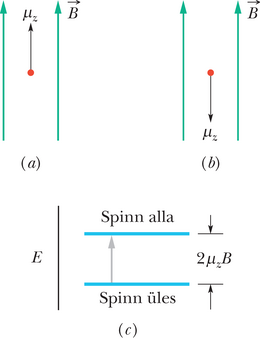
Punktis 32-7 mainisime, et prootonil on magnetiline spinndipoolmoment $\to μ$ , mis on seotud selle siseomase spinnimpulsimomendiga $\to S$ . Kuna prooton on positiivse laenguga, on mõlemad vektorid samasuunalised. Kui prooton asub $z$ -telje suunalises magnetväljas $\to B$ , siis on vektoril $\to μ$ kaks võimalikku orientatsiooni: $+ μ_{z}$ , kui $\to μ$ on väljaga
$\to B$ ühes suunas (joonis 40-10a), või $- μ_{z}$ , kui see on vastassuunas (joonis 40-10b).

Valem 28-38 $(U (θ) = - μ \cdot \to B)$ näitab, et magnetdipooli potentsiaalne energia sõltub $\to μ$ orientatsioonist väljas $\to B$ nõnda, et energia on seotud kahe vastassuunaga joonisel 40-10. Orientatsioon 40-10a („spinn üles”, $↑$ , $S_{z}$ on $\to B$ suunas) on madalama ja orientatsioon 40-10b („spinn alla”, $↓$ ) kõrgema energiaga. Nende kahe seisundi energiate vahe on

(40-21)

Δ E = μ_{z} B - (- μ_{z} B) = 2 μ_{z} B

Kui viime ampullitäie vett magnetvälja, siis püüavad vesinikus leiduvad prootonid minna üle madalama energiaga seisundisse. (Hapniku jätame praegu mängust välja.) Iga prooton võib hüpata kõrgema energiaga seisundisse, kui sellele anda footon energiaga

(40-22)

h f = 2 μ_{z} B

Sellist neeldumist nimetatakse magnetresonantsiks, täpsemalt tuumamagnetresonantsiks (TMR; ingl nuclear magnetic resonance, NMR). Seejuures toimuvat spinni komponendi $S_{z}$ pööret nimetatakse spinni pöörakuks (ka spinni kummutuseks; ingl spin flip).

JOONIS 40-11 Etanooli $C H_{3} C H_{2} O H$ tuumamagnetresonantsi spekter. Spektrijooned vastavad energia neeldumisele prootonite spinni pöörakutel. Joonisel on näidatud millistele aatomrühmadele spektrijooned vastavad. Pange tähele, et prootonid rühmas $C H_{2}$ hõlvavad neli erinevat lähiümbrust. Kogu horisontaaltelg vastab magnetvälja piirkonnale, mis on väiksem kui $10^{- 4} T$ .

Pöörakut tingivad footonid langevad raadiosageduste piirkonda. Raadiosagedus rakendatakse katseobjektile väikese pooli abil, mis on mähitud näidise ümber. Raadiosagedusgeneraator tekitab poolis sinusoidaalse voolu sagedusega $f$ . Sama sagedusega võngub muidugi ka elektromagnetväli poolis. Kui $f$ rahuldab seost 40-22, siis saab võnkuv väli edastada objektis olevale prootonile energiakvandi, mis põhjustab spinni pööraku.

Magnetväli $\to B$ valemis 40-22 on tegelikult summaarne magnetväli prootoni asukohas. See on katseseadme tekitatud välise välja ${\to B}_{v ¨ a li}$ ja prootoni lähikonnas asuvate aatomite ja tuumade magnetiliste dipoolmomentide tekitatud sisevälja ${\to B}_{sise}$ vektorsumma. Tehnilistel põhjustel on mugavam varieerida TMRspektromeetris magnetvälja ${\to B}_{v ¨ a li}$ , jättes raadiosageduse $f$ konstantseks. Mõõdetakse raadiogeneraatori energiat. Raadiogeneraatori energiakadude sõltuvus väljast ${\to B}_{v ¨ a li}$ on TMR-spekter. Spektris ilmuvad resonantspiigid neil ${\to B}_{v ¨ a li}$ väärtustel, kus toimub spinni pöörak.

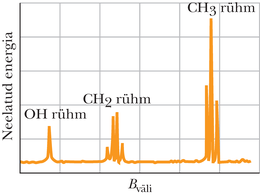
JOONIS 40-12 MRI-aparaati asetatakse hadrosauruse (pardinoka taolise nokaga taimetoitlase) $70$ miljonit aastat vana fossiilne muna, et uurida selle sisemust. Uurimus näitas, et kui muna muiste mattus, pidi see olema värske. (© AP/ Wide World Photos).

Joonisel 40-11 on etanooli ( $C H_{3} C H_{2} O H$ ) TMR-spekter. Etanooli molekul koosneb aatomirühmadest $C H_{3}$ , $C H_{2}$ ja $O H$ . Magnetresonants hõlmab iga rühma prootoneid, kuid igat rühma iseloomustab ${\to B}_{v ¨ a li}$ eri väärtus, sest molekulis ümbritseb igaüht erinev ${\to B}_{sise}$ . Seepärast annavad resonantspiigid joonisel 40-11 etanoolile ainuomase spektri - molekuli signatuuri ehk „sõrmejälje”.

Kuna paljudel ainetel on üksnes neile omane TMR-signatuur, siis kasutatakse tuumamagnetresonantsi ainete identifitseerimiseks, näiteks kriminalistikas. Tuleb märkida, et meditsiinilises diagnostikas rakendatakse laialdaselt magnetresonantskuvamist (magnetic resonance imaging, MRI). Inimkeha eri kudedes leiduvad prootonid asuvad erisugustes magnetkeskkondades. Kui keha või kehaosa on viidud tugevasse magnetvälja, saab neid erinevusi TMR järgi tuvastada. Arvutitöötlusega moodustatakse nende erinevuste järgi kujutis, mis meenutab röntgenkiirte abil saadud kujutisi. Joonis 40-12 esitab selle tehnika kasutusnäite 40-6 | Magnetresonants paleontoloogias.

TMR-katseseadmes hõljub veetilk homogeenses välises magnetväljas

{\to B}_{v ¨ a li}

. Eeldame, et sisevälja

{\to B}_{sise}

võib arvestamata jätta. Vee molekulides sisalduvate prootonite magnetilise dipoolmomendi

z

-komponent

m_{z} = 1, 41 \times 10^{- 26} J /

T. Magnetresonants ilmneb, kui

{\to B}_{v ¨ a li} = 1, 80 T

. Milline on raadiosagedus

f

, mis sunnib prootonite spinni pöörduma ja milline on neelatud footonitele vastav sagedus?

Lahendus

JUHTMÕTTED (1) Kui prooton asub välises magnetväljas $B_{v ¨ a li}$ , on sel oma magnetilise dipoolmomendi tõttu potentsiaalne energia. (2) Sellel potentsiaalsel energial saab olla vaid kaks väärtust, väärtuste vahega $2 μ_{z} B$ . (3) Kui prooton läheb ühelt neist energiatest teisele (spinni pöörak), peab valemi 40-22 kohaselt footoni energia $h f$ olema võrdne selle energiavahega $2 μ_{z} B$ .

Arvutused: asendame valemis 40-22 $B = B_{v ¨ a li} = 1, 80 T$ , leiame

f = \frac{2 μ_{z} B}{h} = \frac{(2) (1, 41 \times 10^{- 26} J / T) (1, 80 T)}{6, 63 \times 10^{- 34} J \cdot s} = 7, 66 \times 10^{7} H z = 76, 6 M H z - --------- - - --------- -

See on spinni pöörakuprotsessis neelatud footonite sagedus; see peab olema ka raadiogeneraatori sagedus ja samuti ka genereeritud elektromagnetvälja sagedus. Nende footonite lainepikkus on

λ = \frac{c}{f} = \frac{3, 00 \times 10^{8} m / s}{7, 66 \times 10^{7} H z} = 3, 92 m - ------ - - ------ -

See sagedus on FM-raadio lainealas.

Pauli keeluprintsiip

Eelmises, 39. peatükis, käsitlesime elektronide mitmesuguseid püüniseid, alates fiktiivsetest ühemõõtmelistest ja lõpetades kolmemõõtmelise reaalse vesiniku aatomiga. Kõigisse neisse sulustasime üheainsa elektroni. Enne, kui asuda tutvuma lõksudega, millesse on püütud mitu elektroni, peame omandama printsiibi, mis kehtib kõikide osakeste kohta, millede spinnkvantarv s ei võrdu nulli ega ka mõne täisarvuga. See ei kehti üksnes elektronide, vaid ka prootonite ja neutronite kohta, milledel kõikidel on $s = \frac{1}{2}$ . Printsiibi püstitas 1925. aastal Wolfgang Pauli ja seda tuntakse Pauli keeluprintsiibina ehk välistusprintsiibina. Elektronide kohta kõlab see nii:

ühte ja samasse püünisesse sulustatud kahel elektronil ei saa olla ühesugust kvantarvude komplekti.

Sellest printsiibist järeldub, et aatomis ei saa olla kahte elektroni, mille nelja kvantarvu väärtused $n$ , $ℓ$ , $m_{ℓ}$ ja $m_{s}$ oleksid ühed ja samad. Vähemalt üks neljast peab olema erinev. Kuid kõikidel elektronidel on üks ja sama spinnkvantarv $s = \frac{1}{2}$ . Kui see nii ei oleks, tabaks aatomeid kollaps ja ei meid teiega ega ka kogu maailma poleks olemas.

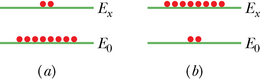
Mitu elektroni nelinurkses lõksus

Sissejuhatuseks vaatame kaht elektroni nelinurkses püünises, mida kirjeldati 39. peatükis. Lisaks seal sissetoodud kvantarvudele arvestame nüüd ka kummagi elektroni spinnimpulsimomente. Oletame, et püünis asub homogeenses magnetväljas. Siis, vastavalt valemile 40-12 ( $S_{z} = m_{s} ℏ$ ), võib elektron olla kas seisundis $↑$ või $↓$ , vastavalt $m_{s} = + \frac{1}{2}$ või $m_{s} = - \frac{1}{2}$ . (Eeldame, et väli on nii nõrk, et me ei pruugi väljast tingitud potentsiaalset energiat arvesse võtta.)

Elektrone püünistesse paigutades peame arvestama Pauli keeluprintsiipi: elektronidel ei tohi olla ühesugused kvantarvude komplektid.

Ühemõõtmeline püünis (joonis 39-2). Elektroni seisundi potentsiaaliaugus laiusega $L$ määrab üksainuke kvantarv $n$ . Seega peab sulustatud elektron olema olekus, millel on teatud kvantarv $n$ ja $m_{s}$ võib olla kas $+ \frac{1}{2}$ või $- \frac{1}{2}$ . Kahel elektronil võib olla kas sama $n$ ja erinev $m_{s}$ või sama $m_{s}$ ja erinev $n$ .
Ristkülikukujuline koppel (joonis 39-13). Et sobitada elektroni lainet mõõtmetega $L_{x}$ ja $L_{y}$ , on vaja kahte kvantarvu $n_{x}$ ja $n_{y}$ ; $m_{s}$ võib olla $\pm \frac{1}{2}$ , kokku on siis vaja kolme kvantarvu. Pauli printsiibi järgi peab kummalgi elektronil vähemasti üks kvantarv kolmest olema erinev.
Risttahukas (joonis 39-14). Kolme mõõtmega $L_{x}$ , $L_{y}$ ja $L_{z}$ sobitamiseks kulub kolm kvantarvu $n_{x}$ , $n_{y}$ ja $n_{z}$ , ja $m_{s} = \pm \frac{1}{2}$ , kokku siis neli kvantarvu. Vähemalt üks kolmest peab iga elektroni puhul olema erinev.

Kujutleme, et paneme eelloetletud püünistesse rohkem kui kaks elektroni. Esimesed elektronid hõivavad muidugi madalaimad energiatasemed. Kuid Pauli keeluprintsiip piirab nende arvu. Mis üle lubatu, peavad hõivama juba kõrgemad tasemed. Öeldakse, et madalaim tase on täis ehk täielikult hõivatud. Kui mingil tasemel pole ühtki elektroni, siis on see tühi ehk hõivamata. Vahepealseil juhtudel võib tase olla osaliselt hõivatud. Sulustatud elektronide süsteem, elektronkonfiguratsioon, on esitatav kas tasemete skeemi või kvantarvude
loeteludena.

Koguenergia leidmine

Seame eesmärgiks leida kahe või enama sulustatud elektroni süsteemi summaarse energia iga konfiguratsiooni jaoks.

Lihtsustuseks eeldame, et elektronide vahel pole elektrilist vastastikmõju, s.t jätame arvestamata elektronpaaride potentsiaalse energia. Niisiis, arvutame iga konfiguratsiooni summaarse energia, leides iga elektroni energia eraldi, nii nagu tegime 39. peatükis. Lõpuks liidame leitud energiad. Niiviisi teeme näidisülesandes 40-3 arvutused seitsme elektroni kohta, mis on sulustatud ruudukujulisse koplisse.

Sobiv on näitlikult esitada süsteemi energiad tasemete diagrammil, nii nagu tegime varem ainsa elektroni jaoks. Madalaim tase $E_{p}$ vastab süsteemi põhitasemele, $E_{e e}$ esimesele ergastustasemele, $E_{t e}$ teisele ergastustasemele ja nõnda edasi.

Näidisülesanne 40-3

JOONIS 40-13 (a) Ruudukujulisse kvantkoplisse küljepikkusega $L$ sulustatud elektroni energiatasemete diagramm (energia $h^{2} / 8 m L^{2}$ kordsetes.) Madalaima taseme on hõivanud elektron spinniga alla ( $↓$ ). (b) Kaks elektroni, $↓$ ja $↑$ , täidavad madalaima taseme. (c) Kolmas elektron on asunud kõrguselt järgmisele tasemele. (d) Süsteemi põhioleku konfiguratsioon kõigi seitsme elektroniga. (e) Kolm kvantüleminekut, mis võiksid viia seitsme elektroni süsteemi selle esimesse ergastusseisundisse. (f) Süsteemi energiatasemete diagramm, millel on näidatud kolm madalaima koguenergiaga olekut ( $h^{2} / 8 m L^{2}$ kordsetes).

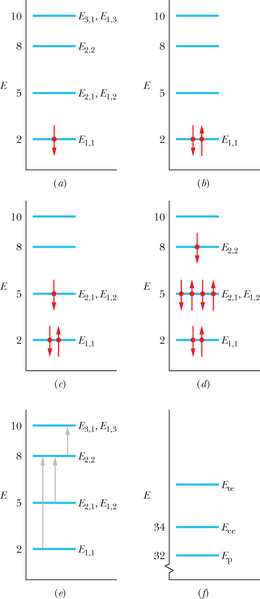
Seitse elektroni on sulustatud ruudukujulisse kvantkoplisse nagu näidisülesandes 39-5, ruudu külgedega $L_{x} = L_{y} = L$ (joonis 40-13). Eeldatakse, et elektronide vahel puudub elektriline vastastikmõju.

Milline on seitsme elektroniga konfiguratsiooni põhiseisund?

Lahendus

Ühe-elektroni-diagramm: võime määrata elektronkonfiguratsiooni, kui paigutame elektrone ühekaupa kvantkoplisse. Kuna me eirame elektronide elektrilist vastastikmõju, võime lähtuda ühe sulustatud elektroni energiatasemete skeemist, mis on toodud joonisel 39-15 ja osaliselt reprodutseeritud joonisel 40-13a. Meenutame, et tasemed on märgistatud kujul $E_{n x, n y}$ . Näiteks on madalaim tase $E_{1, 1}$ ( $n_{x} = 1$ ja $n_{y} = 1$ ).

Pauli printsiip: ühelgi sulustatud elektronil ei tohi olla teistega kokkulangevat kvantarvude $n_{x}$ , $n_{y}$ ja $m_{s}$ komplekti. Esimene elektron läheb madalaimale tasemele $E_{1, 1}$ ja tal võib olla $m_{s} = + \frac{1}{2}$ või $m_{s} = - \frac{1}{2}$ . Valime (meelevaldselt) teise võimaluse ja märgime $↓$ tasemele $E_{1, 1}$ joonisel 40-13a. Samale tasemele „mahub” veel teinegi elektron, kuid sellel peab $m_{s} = + \frac{1}{2}$ , mida joonisel 40-13b tähistab $↑$ tasemel $E_{1, 1}$ .

Lükime elektrone ühekaupa juurde: esimene tase on nüüd täis, kolmas elektron peab minema kidunud tasemele $E_{2, 1} = E_{1, 2}$ kvantarvudega $n_{x} = 1$ ja $n_{y} = 2$ , või $n_{x} = 2$ ja $n_{y} = 1$ . Sellelgi võib olla $m_{s} = + \frac{1}{2}$ või $m_{s} = - \frac{1}{2}$ . Omistame sellele $n_{x} = 2$ , $n_{y} = 1$ ja $m_{s} = - \frac{1}{2}$ ning märgime $↓$ tasemele $E_{2, 1} = E_{1, 2}$ joonisel 40-13c. Samale tasemele mahuvad ka järgmised kolm elektroni tingimusel, et komplekt ( $n_{x}$ , $n_{y}$ , $m_{s}$ ) ei oma duplikaati. Tasemel on siis kokku neli elektroni kvantarvude kogumitega

(2, 1, - \frac{1}{2}), (2, 1, + \frac{1}{2}), (1, 2, - \frac{1}{2}), (1, 2, + \frac{1}{2})

ja tase on nüüd täis. Järgmine elektron peab asuma järgmisele kõrgemale tasemele $E_{2, 2}$ . Olgu selle spinn $m_{s} = - \frac{1}{2}$ .

Joonis 40-13d näitab kõiki seitset elektroni üheelektroni- energiatasemete pildil. See on madalaima energiaga konfiguratsioon, mis rahuldab Pauli keeluprintsiipi. Sama põhioleku konfiguratsioon on koondatud tabelisse 40-2.

Kui suur on seitsme elektroni süsteemi koguenergia

h^{2} / 8 m L^{2}

kordsetes?

Lahendus

JUHTMÕTE Koguenergia $E_{p}$ süsteemi põhiolekus võrdub üksikelektronide energiate summaga süsteemi põhioleku konfiguratsioonis.

Põhioleku energia: iga elektroni energia leiame tabelist 39-1, mis on osaliselt reprodutseeritud tabelis 40-2, või siis näeme seda joonisel 40-13d. Kuna madalaimal tasemel on kaks elektroni, järgmisel neli ja kolmandal üks, saame

E_{p} = 2 (2 \frac{h^{2}}{8 m L^{2}}) + 4 (5 \frac{h^{2}}{8 m L^{2}}) + 1 (8 \frac{h^{2}}{8 m L^{2}}) = 32 \frac{h^{2}}{8 m L^{2}} - ------ - - ------ -

Kui palju energiat peab süsteemile manustama, et see suudaks teha hüppe esimesse ergastusolekusse ja milline on tolle seisundi energia?

Lahendus

JUHTMÕTTED (1) Et süsteemi ergastada, peab üks seitsmest elektronist sooritama kvanthüppe üles energiatasemete skeemil joonisel 40-13d. (2) Võimaldamaks hüpet, peab elektroni (ja seega kogu süsteemi) energiamuut olema $Δ E = E_{k ˜ o rgem} - E_{madalam}$ , kus $E_{madalam}$ on hüppe lähtetaseme ja $E_{k ˜ o rgem}$ lõpptaseme energia. (3) Arvestada tuleb Pauli keeluprintsiipi. Näiteks ei saa elektron hüpata täielikult hõivatud tasemele.

Esimese ergastustaseme energia: käsitleme kolme hüpet joonisel 40-13e. Kõiki neid lubab Pauli printsiip, sest need lõppevad tühjadel või osaliselt hõivatud tasemetel. Ühel näidatuist hüppab elektron $E_{1, 1}$ tasemelt osaliselt täidetud tasemele $E_{2, 2}$ . Energiamuut on

Δ E = E_{2, 2} - E_{1, 1} = 8 \frac{h^{2}}{8 m L^{2}} - 2 \frac{h^{2}}{8 m L^{2}} = 6 \frac{h^{2}}{8 m L^{2}}

(Eeldame, et hüppava elektroni spinni orientatsioon muutub nii, kuidas tarvis.)

Teisel võimalikul hüppel siirdub elektron kidunud tasemelt $E_{2, 1}$ ja $E_{1, 2}$ osaliselt hõivatud tasemele $E_{2, 2}$ . Energiamuut on

Δ E = E_{2, 2} - E_{2, 1} = 8 \frac{h^{2}}{8 m L^{2}} - 5 \frac{h^{2}}{8 m L^{2}} = 3 \frac{h^{2}}{8 m L^{2}}

Kolmandal juhul toimub hüpe $E_{2, 2} \to E_{1, 3}$ , $E_{3, 1}$ . Energiamuut on

Δ E = E_{1, 3} - E_{2, 2} = 10 \frac{h^{2}}{8 m L^{2}} - 8 \frac{h^{2}}{8 m L^{2}} = 2 \frac{h^{2}}{8 m L^{2}}

Neist kolmest kvantsiirdest nõuab viimane kõige vähem energiat. Võime vaadata veel teisigi võimalikke hüppeid, kuid ükski neist ei tarbi vähem energiat. Seega selle süsteemi viib põhiolekust esimesse ergastatud olekusse kvanthüpe $E_{2, 2} \to E_{1, 3}$ , $E_{3, 1}$ ja vajalik energiahulk

Δ E = 2 \frac{h^{2}}{8 m L^{2}} - ----- - - ----- -

Seega on süsteemi esimese ergastusoleku energia $E_{e e}$

E_{e e} = E_{p} + Δ E = 32 \frac{h^{2}}{8 m L^{2}} + 2 \frac{h^{2}}{8 m L^{2}} = 34 \frac{h^{2}}{8 m L^{2}} - ------ - - ------ -

Selle energia ja põhioleku energia $E_{p}$ võime esitada tasemete diagrammil süsteemi jaoks nagu näidatud joonisel 40-13f.

Perioodilisussüsteemi koostamine

Neli kvantarvu $n$ , $ℓ$ , $m_{ℓ}$ ja ms identifitseerivad üksikelektronide kvantseisundeid paljude elektronidega aatomis. Kummatigi pole nende seisundite lainefunktsioonid samasugused kui vesiniku aatomite lainefunktsioonid vastavates olekutes, sest mitmeelektronilises aatomis ei määra elektroni potentsiaalset energiat üksnes tuuma laeng ja asend, vaid ka aatomi kõikide teiste elektronide laengud ja asukohad. Paljuelektroniliste aatomite Schrödingeri võrrandit saab lahendada numbriliselt arvuti abil, vähemasti põhimõtteliselt.

Punktides 39-9 ja 40-3 määratlesime, et kõik seisundid, millede kvantarvud $n$ ja $ℓ$ ühtivad, moodustavad alamkihi. Iga kvantarvu $ℓ$ väärtuse korral on $2 ℓ + 1$ võimalikku magnetkvantarvu $m_{ℓ}$ väärtust ja iga $m_{ℓ}$ kohta tuleb kaks spinnkvantarvu $m_{s}$ väärtust. Seega on alamkihis $2 (2 ℓ + 1)$ seisundit. Kõigil teatava alamkihi seisunditel on üks ja sama energia. Selle suuruse määrab eeskätt arv $n$ , väiksemal määral $ℓ$ .

Et alamkihte mugavamalt tähistada, on kokku lepitud tähistada $ℓ$ väärtusi tähtedega:

Näiteks tähendab alamkiht $3 d$ alamkihti, mille $n = 3$ ja $ℓ = 2$ .

Jagades elektrone paljuelektronilises aatomis alamkihtidesse tuleb muidugi arvestada Pauli keeluprintsiipi (punkt 40-7), mis nõuab, et kahel elektronil aatomis ei või olla ühesugune kvantarvude $n$ , $ℓ$ , $m_{ℓ}$ ja ms komplekt. Kui see ülitähtis printsiip ei kehtiks, siis langeksid kõik elektronid madalaima energiaga olekusse. Ei saaks tekkida erinevaid aatomeid ja molekule, poleks olemas ei keemiat ega biokeemiat ning poleks ka meid teiega. Järgnevalt vaatame mõningate elementide aatomeid, et näha, kuidas Pauli printsiip toimib elementide perioodilisussüsteemi koostamisel.

Neoon

Neooni aatomis on $10$ elektroni. Ainult kaks neist asetub madalaima energiaga $1 s$ alamkihti. Mõlemal on $n = 1$ ja $ℓ = 0$ , $m_{ℓ} = 0$ , kuid ühel neist on $m_{s} = + \frac{1}{2}$ ja teisel $m_{s} = - \frac{1}{2}$ . $1 s$ alamkiht sisaldab $2 [2 (0) + 1] = 2$ seisundit. Kuna sellesse alamkihti Pauli printsiibi järgi rohkem elektrone ei mahu, on see täidetud alamkiht.

Kaks ülejäänud kaheksast elektronist hõivavad järgmise madalaima energiaga $2 s$ alamkihi. Jääb $6$ elektroni, mis asuvad alamkihti $2 p$ ( $ℓ = 1$ ), kuhu mahub $2 [2 (1) + 1] = 6$ elektroni.

Täidetud alamkihis esinevad kõikvõimalikud impulsimomendi $\to L$ projektsioonid $z$ -teljele. Nagu võib kontrollida jooniselt 40-5, on need projektsioonivektorid vastassuunalised ja kompenseeruvad vastastikku. Kompenseeruvad ka kõik spinnimpulsimomendi projektsioonid. Seega pole täidetud alamkihil ei impulsimomenti ega ka magnetmomenti. Alamkihi tõenäosustihedus on kerasümmeetriline. Üheski kolmest täidetud alamkihist ( $1 s$ , $2 s$ ja $2 p$ ) pole „ripakil” elektrone, mis võiksid teiste aatomitega keemilisi sidemeid moodustada. Seepärast on neoon, nagu ka teisedki perioodilisustabeli äärmisse parempoolsesse tulpa kuuluvad väärisgaasid ehk inertgaasid, keemiliselt inertsed.

Naatrium

Neoonile järgneb perioodilisussüsteemis naatrium oma $11$ elektroniga. Kümme neist moodustavad täidetud neoonilaadse südamiku, mille impulsimoment on $0$ . Ainus väljapoole jääv elektron, valentselektron, jääb sellest südamikust kaugele, energeetiliselt järgmisesse $3 s$ alamkihti. Kuna $s$ -kihis on orbitaalne impulsimoment null, siis annab naatriumi aatomi impulsimomendi ja magnetmomendi tervenisti valentselektroni spinn.

Tänu sellele „ripakil” elektronile ühineb naatrium hõlpsasti teiste aatomitega, millede elektronkattes on tühik, kuhu valentselektron sobib. Seepärast on naatrium, nagu ka teisedki perioodilisustabeli vasakpoolse tulba elemendid ehk leelismetallid, keemiliselt aktiivne.

Kloor

Kloori aatomis on $17$ elektroni. Sel on $10$ -elektroniline neoonilaadne täidetud südamik. Üle jääb $7$ elektroni. Kaks neist täidab $3 s$ alamkihi, viis jääb järgmisse, $3 p$ alamkihti. Kuna sellesse mahuks $2 [2 (1) + 1] = 6$ elektroni, siis jääb sinna üks tühik.

Nõnda seostub kloor meelsasti teiste aatomitega, milledel on valentselektron, mis kõlbab selle tühiku täiteks. Näiteks on keedusool $N a C l$ väga püsiv ühend. Kloor, nagu ka teisedki perioodilisustabeli VIIA veergu langevad halogeenid, on keemiliselt aktiivne.

Raud

Raua aatomi $26$ elektroni paigutust alamkihtidesse saab esitada niiviisi:

1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6}      3 d^{6} 4 s^{2}

Alamkihid on järjestatud kvantarvude kasvu kohaselt. Ülaindeks, nagu tavaks, tähistab elektronide arvu alamkihis. Tabelist 40-1 on näha, et $s$ -alamkiht ( $ℓ = 0$ ) mahutab $2$ elektroni, $p$ -alamkiht ( $ℓ = 1$ ) võtab vastu $6$ ja $d$ -alamkiht ( $ℓ = 2$ ) $10$ elektroni. Niisiis moodustavad raua $18$ esimest elektroni viis täidetud alamkihti (neid märgistab allakriipsutus). Tuleb veel leida koht kaheksale elektronile. Kuus neist asub $3 d$ alamkihti, ülejäänud kaks $4 s$ alamkihti.

Miks ei asetu ka viimased kaks elektroni $3 d$ alamkihti? „Ruumi” ju neile seal jätkuks. Põhjus on selles, et konfiguratsioon $3 d^{6}$ $4 s^{2}$ tagab aatomile tervikuna madalama energia kui konfiguratsioon $3 d^{8}$ . Kui elektronid paigutunukski kõik $d$ -kihti, toimuks kähku siire $3 d^{8} \to 3 d^{6} 4 s^{2}$ koos vastava energiaga footoni kiirgumisega. Siit võib õppida seda, et kui lihtsaimad aatomid välja arvata, siis ei täitu seisundid mõnikord nii, nagu nende loogiline järjekord näib dikteerivat.

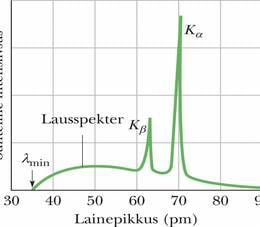
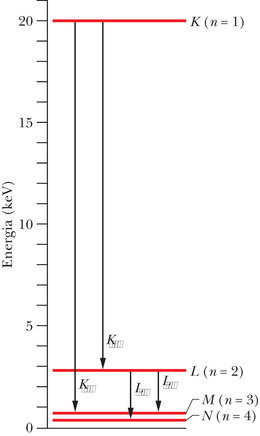
Röntgenkiired ja elementide järjestamine

JOONIS 40-14 Molübdeenile langevate $35 k e V$ energiaga elektronide tekitatud röntgenkiirte jaotus lainepikkuste järgi. Lausspektri ja piikide tekkemehhanism on erinev.

Kui tahkismärklauda (näiteks vaske või volframit) pommitada elektronidega, mille energia on kiloelektronvoltide suurusjärgus, siis tekib lühilaineline elektromagnetkiirgus – röntgenkiirgus. Selle kiirguse paljud rakendused meditsiinis ning tehnikas on hästi tuntud. Järgnevalt selgitame, mida võib röntgenkiirtest välja lugeda aatomite kohta, mis neid neelavad või kiirgavad. Joonisel 40-14 on molübdeenile langevate $35 k e V$ energiaga elektronide tekitatud röntgenkiirte spekter. Näeme laia lausspektrit, millest ulatub välja kaks teravat piiki. Pidev lausspekter ja piigid tekivad eri mehhanismide läbi. Käsitleme neid eraldi.

Röntgenkiirte lausspekter

JOONIS 40-15 Möödudes märklaua aatomist võib elektron kineetilise energiaga $K_{0}$ tekitada röntgenfootoni. Elektron kaotab siis osa oma energiast. Niiviisi kujuneb röntgenkiirguse lausspekter.

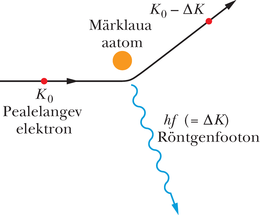
Põrkugu kineetilise algenergiaga $K_{0}$ elektron ühega märklaua aatomitest (joonis 40-15). Elektron võib kaotada energiahulga $Δ K$ , mis muundub põrkepunktist kiirguvaks röntgenfootoniks. (Me ei arvesta siin tühist energiahulka, mis antakse põrkel aatomile, sest aatomi mass on suhteliselt suur.)

Hajutatud elektron (joonis 40-15), mille energia on nüüd juba väiksem kui $K_{0}$ , võib uuesti põrkuda mõne aatomiga, tekitades uue, erineva energiaga footoni. See protsess jätkub seni, kuni elektron jääb peaaegu paigale. Kõik põrgetel genereeritud footonid lisanduvad lausspektrisse.

Selle spektri oluline erisus on piirlainepikkus $λ_{m i n}$ , millest lühemaid laineid ei tekitata. See minimaalne lainepikkus vastab põrkele, milles elektron kaotab kogu oma algse kineetilise energia $K_{0}$ lauppõrkes aatomiga. Vastav minimaalne lainepikkus väljendub seosest

K_{0} = h f = \frac{h c}{λ_{m i n}}

ehk

(piirlainepikkus, 40-23)

λ_{min} = \frac{h c}{K_{0}}

See lainepikkus ei sõltu üldse märklaua materjalist. Kui näiteks vahetada molübdeenist märklaud vasest märklauaga, muutuks kogu spekter, ainult piirlainepikkus jääks samaks.

Kas piirlainepikkus

λ_{m i n}

kasvab, kahaneb või jääb samaks, kui (a) suurendada märklauaga põrkuvate elektronide kineetilist energiat, (b) pommitada elektronidega massiivse märklaua asemel samast ainest õhukest kelmet, (c) valida märklauaks suurema aatomnumbriga element?

Elektronide kimp energiaga

35, 0 k e V

põrkub molübdeenist märklauaga, tekitades röntgenkiiri, mille spekter on joonisel 40-14. Leida piirlainepikkus.

Lahendus

JUHTMÕTE Piirlainepikkus $λ_{m i n}$ vastab elektronile, mis edastab (ligikaudselt) kogu oma energia röntgenfootonile ja seetõttu on footonil suurim võimalik sagedus ja minimaalne lainepikkus.

Arvutus: valemi 40-23 järgi

λ_{m i n} = \frac{h c}{K_{0}} = \frac{(4, 14 \times 10^{- 15} e V \cdot s) (3, 00 \times 10^{8} m / s)}{35, 0 \times 10^{3} e V} 3, 55 \times 10^{- 11} m = 35, 5 p m - ------- - - ------- -

Röntgenkiirte karakteristlik spekter

Pöörame nüüd tähelepanu piikidele $K_{α}$ ja $K_{β}$ joonisel 40-14. Need (ja teised jooniselt välja jäänud piigid) moodustavad märklaua materjali röntgenkiirte karakteristliku spektri.

JOONIS 40-16 Molübdeeni aatomi energiatasemete lihtsustatud skeem. Näidatud on mõningad aukude siirded, mis annavad osa karakteristliku röntgenkiirguse spektrist. Horisontaaljooned esitavad sellise aatomi energiat, mille märgitud elektronkihis on auk.

Piigid tekivad kaheastmelise protsessi kaudu. (1) Elektron põrkub ühega märklaua aatomitest ja hajub sellelt, lüües aatomist välja ühe sügavama elektronkihi ( $n$ väikese väärtusega) elektroni. Kui see süvaelektron juhtub olema kihis, mille $n = 1$ (seda kihti kutsutakse ajaloolistel põhjustel $K$ -kihiks), jääb kihti tühi koht ehk „auk”. (2) Üks elektronidest suurema energiaga kihist siirdub $K$ -kihti ja täidab selle augu. Sel siirdel kiirgab aatom karakteristliku röntgenfootoni. Kui elektron tuleb kihist, mille $n = 2$ (nn $L$ -kihist), siis tekib $K_{α}$ -joon; kui see tuleb kihist $n = 3$ (nn $M$ -kihist), ilmneb $K_{β}$ -joon ja nõnda edasi. $L$ - või $M$ -kihti jääv auk täidetakse elektroniga mõnest tuumast kaugemast kihist.

Röntgenspektrite uurimisel on elektronide hüpete asemel kohasem jälgida augu asendit aatomi elektronpilves. Sedaviisi on joonestatud ka molübdeeni energiatasemete ja siirete skeem joonisel 40-16. Alusjoon $E = 0$ vastab neutraalse aatomi põhiolekule. $K$ -tase vastab molübdeenile auguga $K$ -kihis, $L$ – $L$ -kihis jne.

Noolte $K_{α}$ , $K_{β}$ tähistus joonisel 40-16 vastab spektrijoonte tähistusele joonisel
40-14. Näiteks $K_{α}$ joon tekib, kui $L$ -kihi elektron täidab augu $K$ -kihis. $K_{α}$ -ga tähistatud nool vastab $K$ -kihi augu siirdumisele $L$ -kihti.

Elementide järjestus

Aastal 1913 tekitas Briti füüsik H. G. J. Moseley karakteristlikke röntgenkiiri $38$ elemendist, mis talle sel ajal kättesaadavad olid. Ta ehitas röntgentoru, milles sai eri aineist märklaudu järjestikku nihutada elektronkimpu ilma toru avamata. Röntgenkiirte lainepikkuse määras ta punktis 36-10 kirjeldatud difraktsioonmeetodil, kasutades kristalle difraktsioonivõredena.

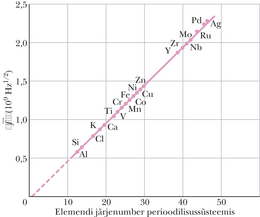
JOONIS 40-17 Moseley graafik $21$ elemendi $K_{α}$ -joone jaoks. Sagedus on arvutatud mõõdetud lainepikkuse järgi.

Nihutades ette järjest uusi elemente, otsis ja leidis Moseley saadud spektreis seaduspärasust. Ta tuvastas, et kui ta kandis graafikule näiteks $K_{α}$ -joonele vastava sageduse $f$ ruutjuure sõltuvuse elemendi järjenumbrist perioodilisussüsteemis, siis langesid punktid sirgele (joonis 40-17). Moseley tegi järelduse:

„Oleme näidanud, et aatomil on mingi siseomadus, mis kasvab korrapäraste astmete kaupa, kui liigume ühelt elemendilt järgmisele. See omadus saab olla ainult selle keskel asuva tuuma laeng.”

Moseley uurimuse järel sai hakata karakteristlikku röntgenspektrit käsitlema elemendi signatuurina. Nüüd oli võimalik lahendada mitmed perioodilisustabeli mõistatused. Varem määrati elemendi asukoht tabelis selle aatomi massi järgi, kuid mitme elemendipaari puhul tuli järjestust muuta, sest seda nõudsid ilmsed keemilised tõigad. Moseley näitas, et elementide õigeks järjestamiseks tuleb aluseks võtta tuumalaeng (aatomnumber $Z$ ). Aastal 1913, enne Moseley tööd, oli perioodilisustabelis mitmeid tühje lahtreid. Ennustati hulgiti uusi elemente. Röntgenspekter andis sellistele ennustustele usaldusväärse kontrollvõimaluse. Lantaniidide hulka kuuluvate elementide (vahel nimetatud ka haruldasteks muldmetallideks) liigitamises oli tublisti segadust, sest nende keemilised omadused on üpris sarnased. Alles Moseley metoodika lubas need õigesti paika panna.

Pole raske mõista, miks elementide karakteristlikud röntgenspekterid reastuvad range regulaarsusega nagu joonisel 40-17, nähtava kiirguse spektrid (optilised spektrid) aga mitte. Elemendi määrab ära selle tuumalaeng. Näiteks iseloomustab kulda tuumalaeng $+ 79 e$ ( $Z = 79$ ). Kui tuumalaeng on ühe võrra suurem, on juba tegemist elavhõbedaga, kui ühe võrra väiksem, siis plaatinaga. $K$ -kihi elektronid, mis määravad oluliselt karakteristliku röntgenspektri väljanägemise, asuvad tuuma lähedal ja on seepärast selle laengu tundlikuks näitajaks. Seevastu optiline spekter tekib väliselektronidevahelistel siiretel. Need on vahepealsete elektronkihtide poolt tuumast eraldatud ja ei ole seepärast tuumalaengu indikaatoriteks.

Moseley graafiku seletus

Moseley eksperimentaalandmeid saaks kasutada elementide korrektseks paigutamiseks perioodilisustabelisse isegi siis, kui selleks puuduks teoreetiline alus. Kummatigi on selline alus olemas.

Vastavalt valemeile 39-32 ja 39-33 on vesiniku aatomi energia

(40-24)

E_{n} = - \frac{m e}{8 ε_{0}^{2} h^{2}} \frac{1}{n^{2}} = - \frac{13, 60 e V}{n^{2}} kus n = 1, 2, 3, \dots

Vaatame nüüd üht paljuelektronilise aatomi $K$ -kihi elektroni. Kuna aatomis on veel teinegi $K$ -kihi elektron, siis „tunnetab” vaatlusalune elektron efektiivset tuumalaengut ligikaudse suurusega $(Z - 1) e$ ; kus $e$ on elementaarlaeng ja $Z$ elemendi aatomnumber. Tegur $e^{4}$ valemis 40-24 on vesiniku tuumalaengu ruudu $e^{2}$ ja elektroni laengu ruudu $(- e)^{2}$ korrutis $e^{2} (- e)^{2}$ . Paljuelektronilise aatomi korral võime arvutada aatomi efektiivset energiat, kui asendame teguri $e^{4}$ korrutisega $(Z - 1)^{2} e^{2} \times (- e)^{2}$ ehk teguriga $e^{4} (Z - 1)^{2}$ . Saame

(40-25)

E_{n} = - \frac{(13, 60 e V) (Z - 1)^{2}}{n^{2}}

Nägime, et $K_{α}$ -footon tekib, kui elektron siirdub $L$ -kihist ( $n = 2$ , $E_{2}$ ) $K$ -kihti ( $n = 1$ , $E_{1}$ ). Siis saame valemi 40-25 järgi energiamuudu

Δ E = E_{2} - E_{1} = \frac{- (13, 60 e V) (Z - 1)^{2}}{2^{2}} - \frac{- (13, 60 e V) (Z - 1)^{2}}{1^{2}} = (10, 2 e V) (Z - 1)^{2}

Siit saame $K_{α}$ -joone sageduseks

(40-26)

f = \frac{Δ E}{h} = \frac{(10, 2 e V) (Z - 1)^{2}}{(4, 14 \times 10^{- 15} e V \cdot s)} = (2, 46 \times 10^{15} H z) (Z - 1)^{2}

Võttes mõlemast poolest ruutjuure, saame

(40-27)

\sqrt{f} = C Z - C

kus konstant $C = 4, 96 \times 10^{7} H z^{1 / 2}$ . Avaldis 40-27 on sirge võrrand. Just see oligi Moseley tulemus (vt joonis 40-17).

Elektronidega pommitatakse koobaltist märklauda ja registreeritakse karakteristliku röntgenkiirguse spekter. Lisaks ilmub teinegi, nõrgem spekter, mille annab koobaltis sisalduv lisand. Spektris ilmnenud Ka-joonte lainepikkused on

178, 9 p m

(koobalt) ja

143, 5 p m

(lisand). Koobaltiaatomis on

27

prootonit (

Z_{C o} = 27

). Määrata neist andmetest lisand.

Lahendus

JUHTMÕTE Nii koobalti ( $C o$ ) kui ka lisandi ( $X$ ) Ka-joonte lainepikkused langevad Ka Moseley sirgele, mille võrrand on 40-27.

Arvutus: asendades $c / λ = f$ valemis 40-27, saame

\sqrt{\frac{c}{λ_{C o}}} = C Z_{C o} - C ja \sqrt{\frac{c}{λ_{X}}} = C Z_{X} - C

Elimineerime $C$ jagades esimese võrrandi teisega, saame

\sqrt{\frac{λ_{C o}}{λ_{X}}} = \frac{Z_{X} - 1}{Z_{C o} - 1}

Paneme sisse algandmed, saame

\sqrt{\frac{178, 9 p m}{143, 5 p m}} = \frac{Z_{X} - 1}{27 - 1}

Lahendame tundmatu suhtes. Leiame, et

Z_{x} = 30, 0 - --- - - --- -

Pilk perioodilisussüsteemi tabelile näitab sedamaid, et lisandiks on tsink. Paneme tähele, et kuna tsingi aatomnumber $Z$ on koobalti omast suurem, on tsingi $K_{α}$ -joone
lainepikkus väiksem.

Laserid ja nende kiirgus

1960ndate aastate alguses andis kvantfüüsika ühe oma olulisima panuse tehnikasse: loodi laserid. Nagu tavalise lambi valguski, tekib laserivalgus siis, kui aatomid siirduvad kõrgema energiaga kvantseisundist madalama energiaga olekusse. Kuid laseris on siirded kooskõlastatud. See tingib laserivalguse järgmised eripärad:

Laserivalgus on ülimalt monokroomaatne. Tavalise elektripirni valgus langeb laia lausspektrisse ja pole üldse monokroomaatne. Tõsi, neoonreklaami valguski on monokroomaatne, kiirgub kitsukesse spektriribasse, mis moodustab $10^{- 6}$ nähtavast spektrist, kuid laserist kiiratu on veelgi kitsamas sagedusribas, mille täpsus on $1 / 1015$ .
Laserivalgus on ülimalt koherentne. Laserist tulevad üksikud lainerodud (lainepaketid, ingl wave trains) võivad olla kilomeetrite pikkused. Kui kaks eraldi kiirt, mis on läbinud nii pikki vahemaid, uuesti kokku juhtida, „mäletavad” need oma ühist päritolu ja võivad moodustada interferentsimustri. Vastav koherentsuspikkus on tavalise elektripirni korral vähem kui meeter.
Laserivalgus on ülimalt suunatud. Laseri kiirtekimp ei lahkne pea üldse; see hälbib rangest paralleelsusest üksnes difraktsiooni tõttu laseri väljundaval. Kui näiteks laserikiir suunati Kuule, et mõõta kaugust Maast Kuuni, tekitas see Kuu pinnal vaid mõnemeetrise läbimõõduga valguslaigu. Ka elektripirni valgust võib koondada läätsede abil ligikaudu paralleelseks kimbuks, kuid see lahkneb siiski laserikiirest palju rohkem. Iga punkt pirni hõõgniidist kiirgab eraldi kiirt ja kogu valgusvihu lahknevuse määravad hõõgniidi mõõtmed.
Laserivalgust saab teravustada üliväikeseks täpiks. Kui kaks valguskiirt kannavad edasi ühesugust energiahulka, siis kiir, mida saab teravustada väiksemaks täpiks, annab täpile suurema heleduse. Laserivalgust saab fokuseerida nii pisikeseks täpiks, et võib kergesti saavutada täpi intensiivsuse $10^{17} W / c m^{2}$ . Võrdluseks: atsetüleenhapnikleegi intensiivsus on vaid $10^{3} W / c m^{2}$ .

Laseritel on palju rakendusi

JOONIS 40-18 Ajulõikuse eel skaneeritakse ja kaardistatakse patsiendi pea laserikiirega (punane). Operatsiooni kestel ühitatakse pea laserkujutis kuvariekraanile kuvatava aju mudeliga, et operatsioonirühm leiaks kätte mudelil rohelisega märgitud alad. (Sam Ogden/ Photo Researchers)

Kõige pisemad laserid, mida kasutatakse heli jm teabe ülekandmiseks kiudoptiliste juhtmete kaudu, on vaid nõelapea suurused. Isegi nii tillukesed laserid võivad olla võimsusega $200 m W$ . Suurimad laserid, mida rakendatakse termotuumasünteesi uuringutes, astronoomilistes kaugusmõõtmistes ning sõjanduses, täidavad terve hoone. Suurimad sedalaadi laserid võivad genereerida lühikesi laserivälkeid, millede võimsus on $10^{14} W$ . See ületab mõnisada korda Ameerika Ühendriikide kõikide elektrijaamade summaarse võimsuse. Et välgatuse ajal ei kustuks kogu riigis valgus, kogutakse nende pikal vaheajal energiat spetsiaalsetesse akumulaatoritesse.

Laserite mitmekesistest rakendustest võiks nimetada vöötkoodi lugejaid kaubamajades, laserplaatide (CD, DVD, BD) valmistamist ja mahamängimist, mitmesuguseid kirurgilisi operatsioone (vt selle peatüki avafotot ja joonist 40-18), maamõõdistust, kangaste juurdelõikust (mitmesajakihilisest kangapaketist), autokerede keevitamist, hologrammide valmistamist.

Kuidas laserid toimivad

Sõna „laser” on lühendsõna, akronüüm ingliskeelsest sõnaühendist

Light
Amplification by
Stimulated
Emission of
Radiation

(Valguse võimendumine stimuleeritud kiirguse kaudu.)

Nagu nimetusestki näha, on stimuleeritud kiirgus laserite funktsioneerimise alus. Stimuleeritud kiirguse mõiste tõi aastal 1917. aastal sisse Albert Einstein. Kuigi maailm pidi ootama 1960. aastani, et näha esimest laserit kiirgamas, oli selle alus rajatud aastakümneid varem.

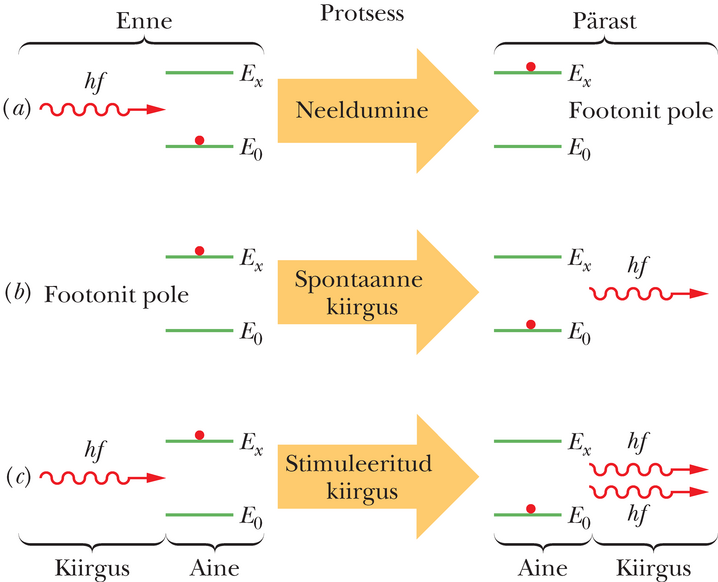
Võtame vaatluse alla isoleeritud aatomi, mis võib eksisteerida kas oma madalaimas, põhiolekus energiaga $E_{0}$ või kõrgemas, ergastatud seisundis energiaga $E_{x}$ . On kolm protsessi, mille kaudu aatom võib neid olekuid vahetada:

Neeldumine. Joonisel 40-19a on aatom algul põhiolekus. Kui aatom on asetatud elektromagnetvälja, mis võngub sagedusega $f$ , võib aatom neelata väljast energiakvandi $h f$ ja tõusta kõrgema energiaga seisundisse. Energia jäävusest järeldub, et
(40-28)
$h f = E_{x} - E_{0}$

See protsess on neeldumine.

JOONIS 40-19 Kiirguse ja aine vastastikmõju (a) neeldumisel, (b) spontaansel kiirgusel ja (c) stimuleeritud kiirgusel. Aine aatomit tähistab punane täpp. Aatom võib olla kas madalamal energiatasemel $E_{0}$ või kõrgemal tasemel $E_{x}$ . Joonise osas (a) neelab aatom footoni $h f$ langevast valguslainest. Osas (b) kiirgab see valguslaine (footoni energiaga $h f$ ). Joonise osas (c) sunnib langev valguslaine (footon $h f$ ) aatomit kiirgama sama energiaga footonit, suurendades valguslaine energiat.

Spontaanne ehk vabakiirgus. Joonisel 40-19b on aatom ergastatud olekus. Väline kiirgus puudub. Hetke pärast siirdub see iseenesest põhiolekusse, kiirates footoni energiaga $h f$ . See on spontaanne kiirgus – spontaanne (ld spontaneus – isetekkeline), sest sündmust ei vallandanud mingi väline mõjur. Tavalise elektripirni valgus tekib just sel moel. Tavaliselt on ergastatud aatomis ergastuse keskmine püsimisaeg ehk ergastuse keskmine eluiga suurusjärgus $10^{- 8} s$ . Kuid mõnedel ergastusseisunditel on eluiga isegi kuni $10^{5}$ korda pikem. Selliseid seisundeid nimetatakse metastabiilseteks; laserites mängivad need seisundid olulist osa.
Stimuleeritud ehk indutseeritud kiirgus. Joonisel 40-19c on aatom taas ergastusseisundis. Kuid nüüd on olemas ka kiirgus valemiga 40-28 määratud sagedusel. Footon energiaga $h f$ saab sundida, stimuleerida (ld stimulare – ergutama, virgutama; stimulus – astel, kepp, näiteks eesliajaja sunniriist) aatomit kiirgama lisafootonit, mille energia on samuti $h f$ . See protsess kannab stimuleeritud kiirguse nime; stimuleeritud, sest kiirgumise ajendab väline footon. Kiiratud footon on igapidi sarnane stimuleerivaga. Kummagi footoniga kaasnevad valguslained on ühisfaasis, neil on sama polarisatsioon ja need kulgevad samas suunas. Joonis 40-19c näitlikustab üksikaatomi stimuleeritud kiirgust.

Kujutleme nüüd, et meil on koos suur arv aatomeid, mis on soojuslikus tasakaalus temperatuuril $T$ . Olgu neid $N_{0}$ põhiolekus energiaga $E_{0}$ ja $N_{x}$ ergastatud olekus energiaga $E_{x}$ . Ludwig Boltzmann andis valemi, mis kirjeldab aatomite jaotumist energiatasemetel:

(40-29)

N_{x} = N_{0} e^{- (E_{x} - E_{0}) / k T}

kus $k$ on Boltzmanni konstant. Valem näib intuitiivseltki igati mõistlik. Korrutis $k T$ on aatomi keskmine kineetiline energia temperatuuril $T$ . Mida kõrgem temperatuur, seda enam aatomeid heidetakse soojusergastuse (s.t aatomite vaheliste põrgete) toimel kõrgema energiaga seisundisse $E_{x}$ . Kuna $E_{x} > E_{0}$ , siis on valemi kohaselt $N_{x} < N_{0}$ : ergastatud olekus on alati vähem aatomeid kui põhiolekus. Skemaatiliselt näitab seda soojusliku tasakaalu seisundit joonis 40-20a.

JOONIS 40-20 (a) Soojuslikus tasakaalus olevate aatomite jaotus põhiseisundi $E_{0}$ ja mingi ergastatud seisundi $E_{x}$ vahel. (b) Erivõtetega saavutatav pöördhõive, millel põhineb laserite talitlus.

Kui nüüd kiiritada joonisel 40-20a kujutatud aatomeid footonitega, millede energia on $E_{x} - E_{0}$ , siis neelavad põhiseisundis olevad aatomid ohtrasti footoneid. Mõnevõrra need genereerivad ka uusi footoneid, stimuleerides väheste ergastatud aatomite kiirgust. Einstein näitas, et mõlema protsessi tõenäosused aatomi kohta on võrdsed. Kuna põhiseisundis on aatomeid rohkem, on neeldumine ülekaalus.

Et genereerida laserivalgust, peab stimuleeritud kiirgus olema ülekaalus. Selleks peab lähtuma seisundist, milles ergastatud aatomite hulk ületab põhiseisundis olevate hulga (joonis 40-20b). Sellist seisundit nimetatakse pöördhõiveks ehk populatsiooni inversiooniks. Kuna leidsime, et seda pole võimalik saavutada soojusergastuse teel, tuleb selleks leiutada kavalaid kaudteid.

Gaaslaser: heelium-neoonlaser

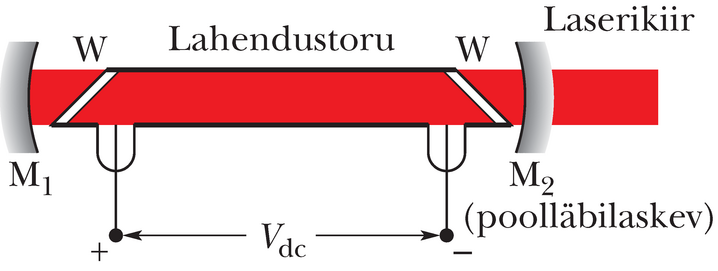
Joonisel 40-21 on heeliumi ja neooni segul töötav laser. See laseritüüp on levinuim üliõpilaste praktikumides. Selle laseri leiutas aastal 1961 Ali Javan koos oma töökaaslastega. Laseri klaastorus on heeliumi ja neooni segu vahekorras $1 : 4$ . Laserikiirgust eritab neoon.

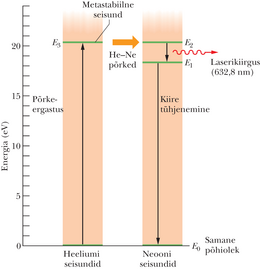
JOONIS 40-21 Heelium-neoonlaseri skeem. Elektroodidele rakendatud pinge $V_{d c}$ kiirendab elektrone läbi lahendustoru, mis sisaldab heeliumi ja neooni gaasisegu. Elektronid põrkuvad gaasis ülekaalus olevate heeliumi aatomitega, mis põrkuvad neooni aatomitega, andes üle oma ergastusenergia. Neooni aatomid kiirgavad footoneid, mis liiguvad piki toru. Läbinud aknad $W$ , peegeldub valgus peeglitelt $M_{1}$ ja $M_{2}$ , stimuleerides uusi aatomeid kiirgama. Osa valgust väljub poolläbipaistva peegli $M_{2}$ kaudu, moodustades laserikiire.

JOONIS 40-22 Heeliumi ja neooni aatomite viis olulist energiataset heeliumneoonlaseris. Laserikiirgus tekib neoonis siiretel $E_{2} \to E_{1}$ , kui tase $E_{2}$ on asustatum kui $E_{1}$ .

Joonisel 40-22 on kummagi gaasi aatomite energiatasemete lihtsustatud skeem. Lahendustorus tekitatakse elektrivool ja selles kihutavad elektronid ergastavad põrgetel heeliumiaatomeid hulgiti metastabiilsele tasemele $E_{3}$ .

Heeliumi seisundi $E_{3}$ energia ( $20, 61 e V$ ) on väga lähedane neooni taseme $E_{2}$ energiale ( $20, 66 e V$ ). Kui metastabiilne ( $E_{3}$ ) heeliumi aatom põrkub põhiseisundis ( $E_{0}$ ) oleva neooni aatomiga kokku, kandub heeliumi ergastusenergia tasemete ligiduse tõttu hõlpsasti neooni aatomile, mis tõuseb olekusse $E_{2}$ . Niiviisi saavutatakse pöördhõive: neooni taseme $E_{2}$ asustatus ületab taseme $E_{1}$ hõivet.

Pöördhõivet on suhteliselt lihtne saavutada, sest (1) algselt puuduvad neooni aatomid olekus $E_{1}$ ; (2) heeliumi taseme $E_{3}$ metastabiilsus tagab seisundis $E_{2}$ olevate neooni aatomite ohtra varu ja (3) neooni tase $E_{1}$ tühjeneb nobedasti neooni põhiolekusse $E_{0}$ (joonisel märkimata vahetasemete kaudu).

Kui neooni aatomi spontaansel siirdel $E_{2} \to E_{1}$ kiiratakse footon, vallandab see
stimuleeritud siirete kaskaadi. Kähku kujuneb laseritoru telge mööda kulgev koherentne punane valgusvoog lainepikkusel $632, 8 n m$ . See hakkab pendeldama peeglite $M_{1}$ ja $M_{2}$ vahel, ajendades iga käiguga üha uusi stimuleeritud kiirgusakte. Kuna $M_{2}$ on poolläbipaistev, siis väljub selle kaudu osa valgust, moodustades laseri kiire.

Laseri

A

(heelium-neoonlaseri) valguse lainepikkus on

632, 8 n m

, laseri

B

(süsinik-dioksiidlaseri) oma

10, 6 m m

, laseril

C

(gallium-arseniidpooljuhtlaseri)

840 n m

. Järjesta laserid nende kvantolekute vahemike järgi, millelt kiirgus tekib, alates suurimast.

Näidisülesanne 40-6

Heelium-neoonlaseris tekib neooni aatomi kahe ergastatud seisundi vahelistel siiretel laserikiir. Paljudes laseritüüpides aga tagavad laseritoime siirded ergastusoleku ja põhioleku vahel, nagu joonisel 40-20b.

Võtame vaatluse alla viimati mainitud tüüpi laseri, mis kiirgab lainel

λ = 550 n m

. Kui pöördhõivet pole veel tekitatud, siis milline on seisundite

E_{x}

ja

E_{0}

asustatuse suhe, kui aatomid on toatemperatuuril?

Lahendus

JUHTMÕTTED (1) Asustatuse suhe $N_{x} / N_{0}$ , mille määrab soojuslik ergastus, on arvutatav valemist 40-29, mille kirjutame ümber kujul

N_{x} / N_{0} = e^{- (E_{x} - E_{0}) / k T}

Et siit Nx/N0 leida, tuleb määrata energiate vahe Ex – E0 nende seisundite vahel. (2) Selle saab määrata laserikiirguse lainepikkusest $550 n m$ .

Arvutus: laserikiirguse lainepikkusest leiame

E_{x} - E_{0} = h f = \frac{h c}{λ} = \frac{(6, 63 \times 10^{- 34} J \cdot s) (3, 00 \times 10^{8} m / s)}{(550 \times 10^{- 9} m) (1, 60 \times 10^{- 19} J / e V)} = 2, 26 e V

Valemi 40-30 kasutamiseks on vaja veel aatomite keskmist soojusenergiat $k T$ toatemperatuuril ( $300 K$ ):

k T = (8, 62 \times 10^{- 5} e V / K) (300 K) = 0, 0259 e V

kus $k$ on Boltzmanni konstant.

Asetades saadud arvud valemisse 40-30, saame

N_{x} / N_{0} = e^{- (2, 26 e V) / (0, 0259 e V)} \approx 1, 3 \times 10^{- 38} - ---------- - - ---------- -

See on üliväike arv, kuid selle väiksus on igati mõistetav, sest ilmselt ei edasta aatomid keskmise soojusenergiaga $0, 0259 e V$ just sageli energiahulka $2, 26 e V$ põrkel teise aatomiga.

Kui tingimused jäävad samaks mis ülesande osas (a), siis millisel temperatuuril on suhe

N_{x} / N_{0} = \frac{1}{2}

?

Lahendus

Arvutus: nüüd tahame teada temperatuuri, millel soojusliikumine on põrgatanud märgatava osa aatomitest kõrgemale energiatasemele. Asendame suhte $N_{x} / N_{0} = \frac{1}{2}$ valemisse 40-30 ja võtame kummastki poolest naturaallogaritmi, leiame $T$ :

T = \frac{E_{x} - E_{0}}{k (ln 2)} = \frac{2, 26 e V}{(8, 62 \times 10^{- 5} e V / K) (ln 2)} = 38000 K - ------- - - ------- -

See on palju kõrgem kui Päikese pinnatemperatuur. Selge siis, et pöördhõive saavutamiseks on vaja mingit erimehhanismi, et aatomeid „üles pumbata”. Soojusliku ergastusega pole pöördhõive saavutatav.

Summary

Aatomite energia on kvanditud, eri kvantseisunditele vastavad erinevad energiad. Aatomid võivad siirduda ühest kvantseisundist teise, kiirates või neelates footoni. Vastava footoni sageduse $f$ määrab seos

h f = E_{k ˜ o rgem} - E_{madalam}

kus $E_{k ˜ o rgem}$ on siirdes osaleva kõrgema ja $E_{madalam}$ madalama taseme energia. Ka aatomite impulsimomendid ja magnetilised dipoolmomendid on kvanditud.

Aatomisse sulustatud elektronil on orbitaalne impulsimoment $\to L$ , mille suurus avaldub valemiga

L = \sqrt{l (l + 1)} ℏ

kus $l$ on orbitaalkvantarv (võib omandada tabelis 40-1 esitatud väärtusi) ja konstant $ℏ = h / 2 π$ . Vektori $\to L$ projektsioon $L_{z}$ suvalisele z-teljele on kvanditud; see on mõõdetav ja võib omandada väärtusi

L_{z} = m_{l} ℏ

kus $m_{l}$ on orbitaalne magnetkvantarv (võimalikud väärtused on toodud tabelis 40-1). Elektroni impulsimomendiga on seotud orbitaalne magnetiline dipoolmoment ${\to μ}_{orb}$ , mis on vektoriga $\to L$ vastassuunaline.

{\to μ}_{orb} = - \frac{e}{2 m} \to L

kus miinusmärk vihjab vastassuunalisusele. Vektori ${\to μ}_{orb}$ projektsioon z-teljele ${\to μ}_{orb, z}$ on kvanditud, mõõdetav ja võib omandada väärtusi

μ_{orb, z} = - m_{l} μ_{B}

kus $m_{B}$ on Bohri magneton

μ_{B} = \frac{e h}{2 π m} = 9, 27 \times 10^{- 24} J/T

Elektronil, olgu see siis sulustatud või vaba, on spinnimpulsimoment (ehk lihtsalt spinn) $\to S$ , mille suuruse annab valem

S = \sqrt{s (s + 1)} ℏ

kus $s$ on elektroni spinnkvantarv, mis on alati $1 / 2$ . Vektori $\to S$ projektsioon $S_{z}$ suvalisele z-teljele on kvanditud, mõõdetav ja omandab väärtusi

S_{z} = m_{s} ℏ

kus $m_{s}$ on elektroni spinnmagnetkvantarv, kas $+ 1 / 2$ või $- 1 / 2$ . Nii vabal kui ka sulustatud elektronil on spinnimpulsimomendiga $\to S$ seotud siseomane magnetdipool magnetiline spinndipoolmomendiga ${\to μ}_{s}$ , mis on vektoriga $\to S$ vastassuunaline:

{\to μ}_{s} = - \frac{e}{m} \to S

Vektori ${\to μ}_{s}$ projektsioon suvalisele z-teljele on kvanditud, mõõdetav ja väärtustega

μ_{s, z} = - 2 m_{s} μ_{B}

Prootonil on siseomane spinnimpulsimoment $\to S$ ja sellega seotud magnetiline spinndipoolmoment, mis on alati spinnimpulsimomendiga $\to S$ samasuunaline. Kui prooton asub magnetväljas $\to B$ , siis vektori $\to μ$ projektsioon z-teljele (mis suunatakse piki $\to B$ suunda) $m_{z}$ omandab üksnes kaks kvanditud väärtust: väljaga $\to B$ samasuunaline ja vastassuunaline. Energiavahe nende orientatsioonide vahel on $2 m_{z} B$ . Et pöörata spinni ühest orientatsioonist teise (spinni pöörak), on vaja footonit energiaga

h f = 2 μ_{z} B

Üldiselt on vektor $\to B$ magnetresonantsi seadme tekitatud välise välja ${\to B}_{v ¨ a li}$ ja prootonit ümbritsevate aatomite ja nende tuumade tekitatud sisevälja ${\to B}_{sise}$ vektorsumma. Spinni pöörakuid registreerides saadakse tuumamagnetresonantsi (TMR) spektrid, millede järgi saab aineid identifitseerida.

Aatomites või muudes lõksudes olevad elektronid järgivad Pauli keeluprintsiipi ehk välistusprintsiipi: ühte ja samasse püünisesse sulustatud kahel elektronil ei saa olla ühesugust kvantarvude komplekti.

Perioodilisustabelis on elemendid järjestatud aatomnumbri $Z$ kasvu järjekorras. Aatomi tuumalaeng on $Z e$ . Prootonite arv tuumas ja elektronide arv neutraalses aatomis on $Z$ .

Seisundid kvantarvu $n$ ühesuguse väärtusega moodustavad elektronkihi, ühesuguse $n$ ja $l$ väärtusega seisundid aga alamkihi. Täidetud kihtidel ja alamkihtidel, mis sisaldavad maksimaalset võimalikku arvu elektrone, puudub impulsimoment ja magnetmomendid (s.t need on võrdsed nulliga).

Röntgenkiirte lausspekter (pidev spekter) tekib, kui suure energiaga elektronid kaotavad tuumadega põrkudes energiat. Piirlainepikkus $λ_{min}$ kiiratakse, kui elektronid kaotavad kogu oma energia ainsas põrkes; see võrdub

λ_{min} = \frac{h c}{K_{0}}

kus $K_{0}$ on põrkuvate elektronide algne kineetiline energia. Karakteristliku röntgenspektri annavad suure energiaga elektronid, mis löövad elektrone aatomi sügavamaist elektronkihtidest välja. Kui sügavamasse kihti tekkinud augu täidab elektron mõnest välimisest kihist, kiiratakse karakteristliku kiirguse footon.

Briti füüsik H.G.J. Moseley mõõtis aastal 1913 ära terve rea elementide karakteristlikud röntgenkiirguse spektrid. Ta tuvastas, et kui kanda graafikule ruutjuur röntgenkiirguse footoni sagedusest sõltuvana elemendi aatomnumbrist $Z$ , saadakse sirge joon (Moseley graafik, joonis 40-17). Siit järeldas Moseley, et elemendi asendit perioodilisustabelis ei määra mitte selle aatomi mass vaid aatomnumber $Z$ .

Laserivalgus tekib stimuleeritud siiretel, see on stimuleeritud kiirgus, mis kiiratakse, kui footon sagedusega

h f = E_{x} - E_{0}

sunnib aatomit siirduma kõrgemalt energiatasemelt $E_{x}$ madalamale tasemele $E_{0}$ . Siis kiiratakse sundivale footonile lisaks sellega identne footon sagedusega $f$ . Et stimuleeritud kiirgus saavutaks ülekaalu neeldumise üle, peab kahe energiataseme vahel laserkiirguri aatomites olema pöördhõive, s.t kõrgemal tasemel peab olema rohkem aatomeid kui madalamal.

Küsimused

Elektron on elavhõbedaaatomi alamkihis

3 d

. Millised

m_{ℓ}

väärtustest on võimalikud:

- 3

,

- 1

,

0

,

1

,

2

?

Uraani aatomis on täidetud

6 p

ja

7 s

alamkihid. Kummas on rohkem elektrone?

Hõbeda aatomis on täidetud

3 d

ja

4 d

alamkihid. Kummas on rohkem elektrone või on mõlemas ühepalju?

Kulla aatomis on üks elektron seisundis, mille

n = 4

. Millised järgmistest

ℓ

väärtustest talle kõlbavad:

- 3

,

0

,

2

,

3

,

4

,

5

?

Kui palju (a) alamkihte, (b) elektroni seisundeid on

n = 2

kihis? (c) Aga

n = 5

kihis?

Joonisel 40-23 on näidatud kolm punkti, milles elektron spinniga üles võib asuda mittehomogeenses magnetväljas (gradiendiga piki z-telge). (a) Järjesta punktid elektroni sisemise magnetdipoolmomendi

{\to μ}_{s}

potentsiaalse energia

U

järgi, alates kõige positiivsemast. (b) Mis suunas mõjub elektronile spinniga üles jõud punktis

2

?

Märgi, kas järgmised väited on tõesed või väärad. (a) Üks (ja ainult üks) järgmistest alamkihtidest on võimatu:

2 p

,

4 f

,

3 d

,

1 p

. (b) Kvantarvu

m_{ℓ}

lubatud väärtuste hulk sõltub üksnes kvantarvust

ℓ

, mitte aga kvantarvust

n

. (c) On neli alamkihti, mille

n = 4

. (d) Antud

ℓ

jaoks on vähim

n

väärtus

ℓ + 1

.(e) Kõikides olekutes, mille

ℓ = 0

, on ka

m_{ℓ} = 0

. (f) Iga

n

väärtuse kohta on

n

alamkihti.

On antud kolm aatomite paari. Kummast aatomist igas paaris on kergem eemaldada elektroni: (a) krüptoon või broom, (b) rubiidium või tseerium, (c) heelium või vesinik?

Millistest kvantarvudest sõltub elektroni energia (a) vesiniku aatomis, (b) vanaadiumi aatomis?

Joonisel 40-14 on

35, 0 keV

elektronidega pommitatava molübdeeni (

Z = 42

) röntgenspekter. Kui molübdeeni asemel valida märklauaks hõbe (

Z = 47

), kas siis (a)

_{min}

, (b)

K_{α}

-joone lainepikkus, (c)

K_{β^{-}}

joone lainepikkus kasvab, kahaneb või jääb muutumatuks?

Joonisel 40-22 on heelium-neoonlaseris toimivate aatomite energiatasemete osalised skeemid. On teada, et heeliumi aatom seisundis

E_{3}

põrkub põhiseisundis neooni aatomiga ja tõstab selle tasemele

E_{2}

. Heeliumi aatomi energia tasemel

E_{3}

(

20, 61 eV

) on lähedane, kuid mitte täpselt võrdne neooni aatomi energiaga tasemel

E_{2}

(

20, 66 eV

). Kuidas on energia ülekanne võimalik, kui need energiad pole täpselt võrdsed?

Vaatame elemente krüptoon ja rubiidium. (a) Kumb neist on sobivam kasutamiseks Sterni ja Gerlachi katses (joonis 40-8)? (b) Kumb ei kõlba üldse, või ei kõlba kumbki?

Röntgenjoon

K_{α}

tekib tänu siirdele

K

-kihi (

n = 1

) ja

L

-kihi (

n = 2

) vahel. Joonisel 40-14 näib, et see joon (molübdeenilt) vastab ainsale lainepikkusele. Kõrgema lahutusvõimega spektromeetris lõheneb see joon mitmeks komponendiks, sest

L

-kiht vastab mitmele energiaväärtusele. (a) Mitu komponenti on

K_{α}

-joonel? (b) Aga

K_{β}

-joonel?

Milline (või kas ükski) järgnevaist seikadest siiretel kahe energiataseme vahel on oluline laseri toimimiseks. (a) Ülemisel tasemel on rohkem aatomeid kui alumisel. (b) Ülemine tase on metastabiilne. (c) Alumine tase on metastabiilne. (d) Alumine tase on aatomi põhitase. (e) Laseri kiirguraineks on gaas.

Ülesanded

KONTROLLKÜSIMUS 1

Näidisülesanne 40-1

Näidisülesanne 40-2

(a)

(b)

(c)

KONTROLLKÜSIMUS 2

Näidisülesanne 40-4

Näidisülesanne 40-5

KONTROLLKÜSIMUS 3

(a)

(b)

Aatomite mõned omadused

Impulsimomendid ja magnetilised dipoolmomendid

Spinn ja magnetresonants

Pauli keeluprintsiip

Perioodilisussüsteemi koostamine

Röntgenkiired ja elementide järjestamine

Laserid ja nende kiirgus