Kuidas viia läbi usaldusväärset mõõtmist?	GPS ja auto spidomeeter mõõdavad auto kiirust erinevalt ja annavad ka erinevaid tulemusi. Kumba uskuda?

Nüüd peaks olema selge, miks usaldatav mõõtetulemus tuleb alati esitada koos mõõtemääramatusega. Mõõtemääramatuse hindamiseks on erinevaid meetodeid, kuid üldjoontes eksisteerib kaks põhilist hinnangu tüüpi. Need on A-tüüpi ja B-tüüpi hinnangud, mida sageli nimetatakse ka A-tüüpi ja B-tüüpi mõõtemääramatusteks. Tuleb rõhutada, et viimane nimetusviis on veidi eksitav, sest mõõtemääramatus on olemuslikult terviklik, erinevad vaid tema hindamise meetodid. A-tüüpi ja B-tüüpi hinnangud on nagu kaks tasapinnalist või kahemõõtmelist kujutist ühtsest ruumilisest objektist nimega mõõtemääramatus. Suutmata kolmemõõtmelist objekti kohe tervikuna hoomata, teeme objektist kahemõõtmelisi fotosid ja püüame nende põhjal saada ettekujutust tervikust. Analoogiliselt konstrueerime A-tüüpi ja B-tüüpi mõõtemääramatuste põhjal liitmääramatuse. Sellest täpsemalt allpool.

Kui me kordusmõõtmisi tehes saame kogu aeg veidi erinevaid tulemusi, nii et iga konkreetne mõõteväärtus varem saadutega üldjuhul kokku ei lange, siis peame andma mõõtemääramatusele A-tüüpi hinnangu. A-tüüpi mõõtemääramatus on põhjustatud juhuslikest mõjuritest ja see leitakse kordusmõõtmiste tulemustest matemaatilise statistika meetoditega. A-tüüpi määramatust saab mõõtmiste arvu suurendamisega vähendada. 

Järgnevalt vaatleme A-tüüpi mõõtemääramatuse hindamisel kasutatavaid matemaatilise statistika valemeid, mille peast teadmine ja isegi rakendamise oskus käesoleva kursuse läbimiseks vajalikud ei ole, kuna kõik kirjeldatud tehted sooritab tänapäeval arvuti. Kui me oleme saanud konkreetsele mõõtesuurusele kokku n üldjuhul erinevat üksikut mõõteväärtust ehk mõõdist x₁, x₂, x₃, … x_n, siis on parimaks lähenduseks suuruse tõelisele väärtusele mõõdiste aritmeetiline keskmine ehk keskväärtus. Selle saamiseks liidame kõik mõõdised kokku ning jagame läbi mõõdiste arvuga n

Mõõdiste hajumist keskväärtuse ümber iseloomustatakse dispersiooniga D(x), mille me saame, töödeldes mõõdiste x_i erinevusi keskväärtusest ehk vahesid ( x – x_i ).

Need vahed võivad olla nii positiivsed kui ka negatiivsed, sõltuvalt sellest, kas üksik mõõteväärtus (mõõdis x_i) on keskväärtusest väiksem või suurem. Kui me liidaksime lihtsalt vahesid, siis hakkaksid nad vastastikku kompenseeruma ja summa ei sisaldaks enam infot tulemuste hajuvuse kohta. Seetõttu peame liitma vahede ruutusid, mis on alati positiivsed. Saadud summat me ei jaga enam mõõteväärtuste arvuga n, vaid sellest ühe võrra väiksema arvuga n – 1, sest teades keskväärtust ning kõiki üksiktulemusi peale ühe, on võimalik puuduv viimane tulemus välja arvutada. Info tema kohta sisaldub keskväärtuses. Ühtekokku saame dispersiooni valemi

Rangelt võttes iseloomustab dispersioon mitte üksikute mõõteväärtuste ehk mõõdiste hajuvust, vaid mõõdiste ruutude hajuvust sest liideti ju vahede ruutusid. Et jõuda mõõdiste endi hajuvust kirjeldava suuruseni, tuleb dispersioonist võtta ruutjuur: 

Nii saadud suurust s(x) nimetatakse mõõdise eksperimentaalseks standardhälbeks. Pikk nimetus tuleneb asjaolust, et matemaatilises statistikas on lubatud nimetada lihtsalt standardhälbeks vaid lõpmata suure arvu üksiktulemuste töötlemisel saadavat suurust. Meie mõõtmistulemuste arv on kindlasti lõplik. Praktilises metroloogias aga pole kombeks nii range olla – suurust s(x) nimetatakse lihtsalt üksikmõõtmise standardhälbeks ja tähistatakse tavaliselt kreeka tähega σ (sigma). Kaasajal võib üksikmõõtmise standardhälbe lasta leida mistahes tabelarvutusprogrammil (näiteks MS Excel), kasutades funktsiooni STDEV või STDEVA (ingl standard deviation). Ka enamikul funktsioonidega taskuarvutitest on see funktsioon olemas. Vastav klahv kannab tähist σ või STDEV. 

Taskuarvuti näib esmapilgul kirju nagu kosmosekapsli juhtpaneel. Sestap on selle kasutusjuhend põnev lugemismaterjal, mis enamasti ka Internetis saada. Näiteks võib suurte numbrinuppude all peidus olla mõni võimas statistiline funktsioon. Selle arvuti klahvide 4,5 ja 6 all on vastavalt aritmeetilise keskmise, dispersiooni ja standardhälbe funktsioonid.

Standardhälve σ on suurus, mis kirjeldab üksikute mõõteväärtuste puhtjuhuslikku hajumist keskväärtuse ümber. Standardhälvet mõõdetakse alati samades ühikutes nagu mõõtesuurust ennastki. Kui teeksime lõpmata palju mõõtmisi, siis langeks vahemikku otspunktidega „keskväärtus miinus standardhälve“ kuni „keskväärtus pluss standardhälve“ 68% kõigist mõõdistest. Lähemalt uurime seda allpool näite varal (p.2.4.3). Tingivat kõneviisi (langeks) kasutame standardhälbe definitsioonis põhjusel, et praktikas ei tehta ju kunagi lõpmata suurt arvu mõõtmisi. Seetõttu ei pruugi reaalsetel mõõtmistel ülalkirjeldatud vahemikku jääda täpselt 68% kõigist mõõdistest. Aga mida suurem on mõõdiste koguarv, seda väiksem on katses ilmnev erinevus väärtusest 68%.

Tasub märkida, et standardhälvet kasutatakse kõigis loodusteadustes ning isegi sotsiaalteadustes (politoloogias, sotsioloogias, majandusteaduses). Jällegi on füüsika see, mis tekitab paljudele teistele teadustele vajaliku mudeli. Ehkki standardhälve on kõige üldisemal juhul matemaatilise statistika mõiste, selgub tema olemus kõige paremini lihtsatest füüsikakatsetest, mida me allpool (p.2.4.3) ka läbi teeme. 

Kui me oleme teinud mingi keskmistamiseks piisava arvu üksikmõõtmisi (näiteks 10), leidnud nende tulemustest keskväärtuse ja nüüd sama protseduuri kordame, siis märkame, et kaks keskväärtust erinevad oluliselt vähem kui kaks suvalist üksikut mõõteväärtust. Keskmistamine vähendab väärtuste hajuvust. Matemaatilises statistikas näidatakse, et aritmeetilise keskmise standardhälve on üksikmõõtmise standardhälbest väiksem ruutjuur mõõtmiste arvust korda. Aritmeetilise keskmise standardhälvet võib vaadelda standardse A-tüüpi hinnanguna mõõtemääramatusele. Vastavalt nimetatakse seda standardmääramatuseks ja tähistatakse väikese u-tähega: 

Niisiis, piisavalt suure mõõtmiste arvu ja tulemuste puhtjuhusliku hajuvuse korral annab standardmääramatus keskväärtuse usaldatavuseks 68%. Kui me soovime usaldatavust suurendada, siis tuleb standardmääramatust korrutada arvuga, mida nimetatakse katteteguriks. Kattetegur sõltub mõõdiste jaotusest keskväärtuse ümber ja nõutavast usaldusnivoost. Näiteks on mõõdiste puhtjuhusliku hajuvuse ja nõutava usaldatavuse 95% korral kattetegur 1,96 ehk ligikaudu 2. Katteteguriga läbikorrutatud standard­määramatust nimetatakse laiendmääramatuseks ja tähistatakse suure U-tähega. Kui usaldatavus on eraldi ära toodud, siis võib konkreetse suuruse x mõõtemääramatust ikka tähistada Δx-ga, nii nagu me seda ülalpool tegime, ning u-sid mitte kasutada. 

Oluline on mõista sisulist erinevust üksikmõõtmise (ehk mõõdise) standardhälbe ja keskväärtuse standardhälbe vahel. Mõõtmiste arvu n suurendamine ei vähenda üksikmõõtmise standardhälvet. See vaid võimaldab üksikmõõtmise standardhälvet täpsemini määrata. Kahe suvalise juba tehtud mõõtmise tulemused ei hakka sellest omavahel vähem erinema, et me teeme täiendavaid mõõtmisi. Kuid mõõtmiste arvu suurendamisel täpsustub tulemuste jaotuskõvera (vt p.2.4.3) kuju. See aga tähendab ka kõvera maksimumi asukoha (keskväärtuse) – täpsustumist. Just seetõttu väheneb keskväärtuse standardhälve mõõtmiste arvu suurendamisel (valem 2.6). 

Üksikmõõtmise standardhälve iseloomustab tulemuste jaotuskõvera laiust. Valemit 2.2 matkiv kirjutusviis x – σ < x₀ < x + σ, milles mõõtemääramatuse rollis esineb üksikmõõtmise standardhälve σ, ütleb vaid seda, et mõõtesuuruse tõeline väärtus x₀ jääb tõenäosusega 68% väärtuste x – σ ja x + σ vahele. Tõeline väärtus ei erine suvalisest mõõdisest rohkem kui σ võrra. Keskväärtust esile tõstev valemit 2.2. matkiv kirjutusviis

milles mõõtemääramatuse rollis esineb keskväärtuse standardhälve , ütleb juba seda, et keskväärtus ja tõeline väärtus x₀ ei erine rohkem kui keskväärtuse standardhälbe võrra. 

Kui kordusmõõtmised annavad alati sama tulemuse, siis ei saa mõõtemääramatust hinnata kordusmõõtmisi tehes. Sellisel juhul peame andma mõõtemääramatusele B-tüüpi hinnangu. Sageli öeldakse ka, et tegemist on B-tüüpi määramatusega. B-tüüpi hinnang mõõtemääramatusele saadakse mitte enam mõõtja enda poolt rakendatavate statistiliste meetoditega, vaid muudest allikatest pärineva info põhjal. Eelkõige kasutab mõõtja mõõteriista tootja poolt antud infot mõõteriista täpsuse kohta. Kõige suurem erinevus A- ja B-hinnangute vahel ongi see, et B-tüüpi määramatuse korral teeb sisulise töö mõõtemääramatuse hindamisel ära mõõtevahendi või mõõteriista valmistaja. Seejuures kasutab mõõteriista tootja mitmesuguseid nii sama tüüpi mõõteriistaga kui ka palju täpsemate mõõteseadmete abil saadud mõõtetulemusi. Kindlasti ta ka töötleb neid statistiliselt. Tootjad märgivad mõõtemääramatuse alase teabe kas otse mõõteriistale või selle passi. Kui aga selline info puudub, siis on üldine tava võtta mõõtemääramatuseks pool väikseimast skaalajaotisest. 

Reeglina tuleb multimeetri mõõtetulemustele anda B tüüpi määramatuse hinnang, sest selle mõõtevead on süstemaatilised. Näiteks on pildiloleva multimeetri passis 10 V ulatusega alalispinge skaala täpsuseks antud +/- 3%. See tähendab, et sõltumata skaala piires võetud mõõdust on viga +/- 0,3 V. Näiteks 3 V mõõteväärtusest moodustab see 10%, mis on päris palju. Seetõttu on täpsema mõõtmise huvides otstarbekas valida võimalikult mõõteväärtuse lähedane mõõtepiirkond.

Milline võiks olla infrapunakaameraga mõõdetud temperatuuride mõõtemääramatus? Kas selliste mõõtmiste kaudu saab hinnata inimese tervislikku seisundit?

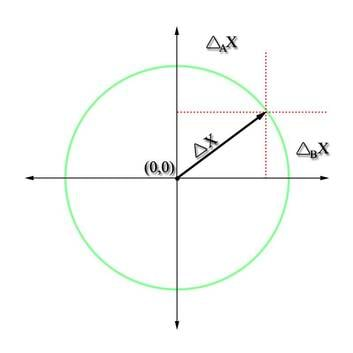
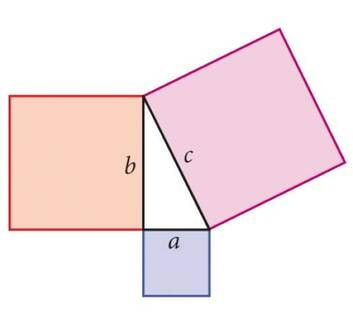
Enamasti esinevad nii A- kui B-tüüpi määramatus korraga. Liitmääramatus leitakse kui ruutjuur A- ja B-määra­matuste ruutude summast. See meenutab täisnurkse kolmnurga hüpotenuusi pikkuse leidmist omavahel ristuvate kaatetite pikkuste kaudu Pythagorase teoreemi abil (joonis 2.2).

Joonis 2.2 A ja B tüüpi mõõtemääramatuse liitmine.

Nii toimides rõhutame, et me üldiselt eeldame A- ja B-tüüpi määramatuste omavahelist sõltumatust. Määramatuste lihtne liitmine tähendaks eeldust, et mõlemast määramatuse liigist tingitud mõõtevead on alati sama märgiga (mõõtevigade vastastikune kompenseerumine on välistatud). Tegelikkuses aga on kompenseerumise (mõõtevigade erimärgilisuse) ja mittekompenseerumise (samamärgilisuse) tõenäosused võrdsed. Kui me oleme piki A-tüüpi määramatuse väärtuste telge tõelisest väärtusest konkreetse A-määramatuse (kui ühe kaateti) võrra eemaldunud, siis võime jätkata liikumist piki eelmisega ristuvat B-tüüpi määramatuse telge võrdse eduga kas positiivses või negatiivses suunas (teise kaateti võrra). Telgede ristseis väljendab A- ja B-määramatuste omavahelist sõltumatust (ühe muutumine ei mõjuta teist). Niisiis eemaldume kokkuvõttes tõelisest väärtusest täisnurkse kolmnurga hüpotenuusi võrra. Tähistades suuruse x A-tüüpi määramatuse sümboliga Δ_Ax ja B-tüüpi määramatuse sümboliga Δ_Bx, võime liitmääramatuse avaldada kujul

Mõõtemääramatuse praktilisel hindamisel esineb ka olukordi, mil kordusmõõtmiste tulemused omavahel erinevad, kuid on vähe alust pidada seda erinevust puhtjuhuslikuks. Järelikult pole mõtet teha väga palju kordusmõõtmisi, et leida nende põhjal standardhälvet. Kordusmõõtmisi tasub siiski teha enesekontrolliks (kas toimisin kogu aeg ühtemoodi?) ja saadud tulemuste  keskmistamiseks, kuna keskväärtus on kindlasti usaldatavam üksikmõõtmisest. Enamasti tekib kõnealune olukord aja mõõtmisel. Oletagem, et me kasutame ajamõõtjat, mille kahe näidu vähim võimalik erinevus ehk lahutuspiir on 0,01 s. See ongi konkreetsel juhul B-tüüpi määramatuse ligikaudseks hinnanguks. Täpsema hinnangu saamiseks peaksime uurima ajamõõtja passi. Mõõtja reaktsiooniaeg ehk ajavahemik signaali saamisest kuni signaalist tuleneva tegevuseni (ajamõõtja nupu vajutamiseni) on aga vahemikus 0,1 kuni 0,2 s, sõltuvalt konkreetsest inimesest. See ületab oluliselt B-tüüpi määramatuse hinnangut, mistõttu viimase täpne väärtus polegi väga tähtis. Mõistlik on kasutada mõõtemääramatuse hinnanguna kas varem mõõdetud isiklikku reaktsiooniaega või teadaolevat inimliku reaktsiooniaja ülapiiri 0,2 s. Lisainfot annab kordusmõõtmiste tulemuste keskmistamine. Oletagem näiteks, et mõõtsime viis korda mingi protsessi kestust ja saime tulemusteks 12,32 s; 12,28 s; 12,23 s; 12,31 s ja 12,26 s. Nende tulemuste keskmine on 12,28 s, üksikmõõtmise ja keskmise suurim erinevus aga 0,05 s, mis ei ületa mõõtja reaktsiooniaega. Kuna reaktsiooniaeg on oluliselt suurem mõõtmiste lahutuspiirist (0,01 s), siis pole eriti mõtet tulemust anda sajandiksekundilise täpsusega. Piisavalt suure usaldatavusega võime lõpptulemuse esitada kujul  (12,3 +/- 0,2) s. 

Märkigem veel, et kui mingi üksiktulemuse erinevus teistest palju kordi ületab ülejäänud tulemuste omavahelist keskmist erinevust, siis on põhjust teistest oluliselt erinev mõõtmistulemus keskmistamisel arvestamata jätta. Suure tõenäosusega on tema saamisel tehtud mõõtmisprotseduuris mingi viga. 

Puuvõrade katvuse hindamine käepäraste vahenditega. Missugune on sellise mõõtmise mõõtemääramatus?	Selle mehaanilise stopperi lahutusvõime on üks sekund. Milline on aga reaktsiooniaja kõrval kella mehaaniline viga? Kui seadme passi pole käepärast, siis rusikareegel ütleb, et veaks tuleb võtta pool vähimast jaotisest, ehk antud juhul 0,5 s.