Füüsika üheks ülesandeks on kirjeldada maailmas eksisteerivaid erinevaid energiavorme, iseäranis neid, mis on olulised tavaolukorras. Üks energia põhiliike on potentsiaalne energia . Korrektselt öeldes on potentsiaalne energia selline energia, mis on seotud kehade vastastikuse asendiga süsteemis, kus kehade vahel mõjuvad jõud.
See üsna formaalne definitsioon käib teile vägagi tuttavate asjade kohta. Tema paremaks mõistmiseks pakume sellise näite: benji-hüppel tõukab hüppaja end lahti platvormilt (joonis 8-1). Süsteem koosneb Maast ja hüppajast. Nende kahe keha vahel mõjub gravitatsioonijõud. Süsteemi olek muutub (kaugus Maa ja hüppaja vahel väheneb – just see teebki hüppe põnevaks). Me võime arvutada hüppaja liikumist ning kineetilise energia juurdekasvu, defineerides gravitatsiooni potentsiaalse energia . See energia on seotud kaugusega kahe teineteist gravitatsioonilise tõmbejõuga mõjutava keha vahel, antud juhul siis hüppaja ja Maa vahel.
Kui kukkumise lõpuosas hakkab hüppaja benji-köit venitama, koosneb süsteem köiest ja hüppajast. Nende vahel mõjub nüüd köie elastsusjõud. Süsteemi olek muutub (köit venitatakse pikemaks). Me võime arvutada hüppaja kineetilise energia vähenemist köie pikkuse suurenemisel, defineerides köie deformatsiooni potentsiaalse energia . See energia on seotud elastse süsteemi, antud juhul benji-köie kokkusurumise või pikenemisega.
Füüsika määratleb, kuidas süsteemi potentsiaalset energiat arvutada nii, et süsteem saaks energiat salvestada või kasutusele võtta. Nii peab enne iga benji-hüpet keegi (eeldatavasti mehaanikainsener) määrama, millist köit kasutada. Selleks tuleb välja arvutada oodatavad gravitatsioonijõu ning elastsusjõu potentsiaalsed energiad ja neid võrrelda – vaid sel juhul on hüpe põnev, aga mitte hukatuslik.
Eelmises, 7. peatükis vaatlesime töö seost kineetilise energia muutusega. Siin vaatleme, kuidas on töö seotud potentsiaalse energia muutumisega.
Viskame jällegi tomatit ülespoole (joonis 8-2). Me juba teame, et sel ajal, kui tomat ülespoole kerkib, on gravitatsioonijõu poolt tehtav töö negatiivne, sest ta viib ära tomati kineetilist energiat. Võime öelda, et gravitatsioonijõud muudab sellesama energia tomatist ja Maast koosneva süsteemi potentsiaalseks energiaks.
Tomati kiirus väheneb, ta jääb seisma ja hakkab siis gravitatsioonijõu mõjul allapoole langema. Nüüd on gravitatsioonijõu töö tomati liikumisel positiivne – ta suurendab tomati kineetilist energiat süsteemi tomat–Maa gravitatsioonilise potentsiaalse energia arvel.
Nii tõusu kui langemise jaoks on gravitatsioonilise potentsiaalse energia muut suuruselt võrdne ja vastasmärgiline tomatile mõjuva gravitatsioonijõu poolt tehtava tööga. Kasutades töö tähistamiseks sümbolit , võime kirjutada
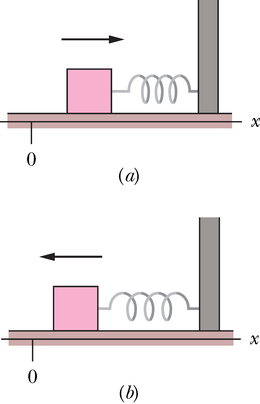
Sama võrrandit saab kasutada ka joonisel 8-3 kujutatud klotsist ja vedrust koosneva süsteemi kohta. Kui me tõukame klotsi, pannes ta liikuma paremale poole, mõjub vedru elastsusjõud vasakule ja teeb klotsi liikumisel negatiivset tööd, muutes klotsi kineetilist energiat süsteemi klots-vedru potentsiaalseks energiaks. Klotsi liikumine aeglustub, ta jääb seisma ja hakkab liikuma vasakule, kuna sinna on endiselt suunatud vedru elastsusjõud. Energia ülekandumine on nüüd vastassuunaline – süsteemi klots–vedru deformatsiooni potentsiaalne energia muudetakse klotsi kineetiliseks energiaks.
Kõigepealt paneme kirja võtmesõnad eespool toodud olukordade kirjeldamiseks:
- Süsteem koosneb kahest või rohkemast kehast.
- Jõud mõjuvad süsteemi kuuluvate, punktmassina käsitlevate kehade (nagu tomat või klots) ning süsteemi ülejäänud osade vahel.
- Kui süsteemi olek muutub, teevad need punktmassi-sarnasele kehale mõjuvad jõud tööd (tähistame selle W1), mis teostab energiavahetust selle keha kineetilise energia ja süsteemi mõnda teist tüüpi energia vahel.
- Kui süsteemi oleku muutus on vastassuunaline (protsess on pööratud), viib vastavate jõudude töö W2 energiat üle vastassuunas (energia ülekanne on pööratud).
Kui olukord on selline, et alati kehtib , on teiseks energia tüübiks potentsiaalne energia ja ülekandes osalev jõud kannab nimetust konservatiivne jõud. Nagu arvata võite, on nii gravitatsioonijõud kui vedru elastsusjõud mõlemad konservatiivsed (vastasel juhul ei saaks me rääkida gravitatsioonilisest potentsiaalsest energiast ja deformatsiooni potentsiaalsest energiast nii, nagu eelnevas tegime).
Jõudusid, mis ei ole konservatiivsed, nimetatakse mittekonservatiivseteks jõududeks. Liikumist pidurdavad hõõrdejõud ja takistusjõud on mittekonservatiivsed. Lükkame näiteks klotsi libisema piki põrandat, mis ei ole hõõrdevaba. Libisemise ajal klotsi ja põranda vahel mõjuv hõõrdejõud aeglustab klotsi liikumist, muutes selle kineetilise energia teist tüüpi energiaks, mida nimetatakse soojusenergiaks (mis on seotud aatomite ja molekulide juhuslike liikumistega). Katsed on näidanud, et seda energia ülekandumist ei saa pöörata (hõõrdejõud ei võimalda muuta soojusenergiat tagasi klotsi kineetiliseks energiaks). Kuigi meil on ka siin süsteem (mis koosneb klotsist ja põrandast) ja selle süsteemi osade vahel mõjuv jõud kannab samuti üle energiat, ei ole see jõud konservatiivne. Järelikult soojusenergia ei ole potentsiaalne energia.
Kui punktmassi omadustega kehale mõjuvad ainult konservatiivsed jõud, saab selle keha liikumisega seostuvaid, tavaliselt keerulisi probleeme oluliselt lihtsustada. Järgmine punkt, kus tuuakse välja jõudude konservatiivsuse tuvastamise põhimõtted, annab meile vahendid nende lihtsustuste tegemiseks.
Määramaks, kas tegemist on konservatiivse või mittekonservatiivse jõuga, tuleb kõigepealt teha järgmine katse: vaatleme jõudu, mis mõjub piki suvalist suletud teed liikuvale punktmassile, mis alustab liikumist mingist punktist ja tuleb lõpuks samasse punkti tagasi (olles seega teinud ringreisi, mis algab ja lõpeb samas kohas). See jõud on konservatiivne ainult siis, kui selle liikumise käigus on ülekantud energia null nii selle kui ka iga teise suletud teekonna korral. Teiste sõnadega:
Kogutöö, mille teeb punktmassile mõjuv konservatiivne jõud ükskõik millise suletud teekonna läbimisel, on null.
Katsetest teame, et gravitatsioonijõud rahuldab seda suletud teekonna tingimust. Näiteks võib tuua joonisel 8-2 üles visatud tomati. See tomat visatakse üles kiirusega ja kineetilise energiaga . Tomatile mõjuv gravitatsioonijõud aeglustab tema liikumist, peatab ta ning sunnib tagasi langema. Kui tomat jõuab tagasi algasendisse, on tema kiirus jällegi ja kineetiline energia . Seega viis gravitatsioonijõud tõusu ajal tomatilt ära täpselt niisama palju kineetilist energiat, kui ta laskumise ajal tagasi tõi. Kogutöö, mille tegi selle suletud teekonna vältel tomatile mõjuv gravitatsioonijõud, on null.
Sellest suletud teekonna tingimusest saab teha olulise järelduse:
Töö, mille teeb punktmassile mõjuv konservatiivne jõud tema liikumisel ühest punktist teise, ei sõltu selle punktmassi liikumistee kujust.
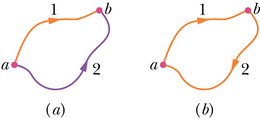
Oletame näiteks, et punktmass liigub joonisel 8-4a punktist punkti kas mööda teed või mööda teed . Kui punktmassile mõjub ainult konservatiivne jõud, on selle töö ühesugune ükskõik kumba teed pidi liikudes. Valemina võiksime selle kirja panna:
kus indeks tähistab liikumise alg- ja lõpp-punkte ning indeksid ja osutavad liikumisteele.
Tulemus on väärtuslik seepärast, et aitab lihtsustada keerulisi ülesandeid juhul, kui tegu on ainult konservatiivsete jõududega. Oletame, et teil on vaja arvutada konservatiivse jõu tööd keha konkreetsel liikumisel ühest punktist teise ja ilma lisainformatsioonita oleks see arvutus raske või isegi võimatu. Nüüd võite aga selle töö arvutamiseks kasutada mõnda teist võimalikku liikumisteed nende punktide vahel, mille jaoks on rehkendus lihtne ja võimalik. Me demonstreerime seda näidisülesandes 8-1, aga kõigepealt peame me tõestama, et valem 8-2 on õige.
Joonisel 8-4b on kujutatud suletud teekond punktmassi jaoks, millele mõjub üksainus jõud. Punktmass liigub lähtepunktist punkti piki teed ja tagasi punkti piki teed . Punktmassile mõjuv jõud teeb tööd mõlema liikumise ajal. Muretsemata selle pärast, milline töö on positiivne või negatiivne, tähistame punktist punkti piki teed liikumisel tehtava töö ja punktist tagasi punkti piki teed liikumisel tehtava töö . Kui jõud on konservatiivne, peab kogutöö suletud teekonnal olema null:
ja
Sõnades öelduna peab töö, mis tehakse ülemist teed pidi liikumisel, olema võrdne ja vastasmärgiline alumist teed pidi tagasi algasendisse liikumisel tehtava tööga.
Vaatleme nüüd olukorda, kus punktmass liigub punktist punkti mööda teed , nagu seda on kujutatud joonisel 8-4a. Kui jõud on konservatiivne, peab selle liikumise käigus tehtav töö olema võrdne ja vastasmärgiline tööga .
Pannes valemis 8-3 asemele , saame
mida oligi tarvis tõestada.
Näidisülesanne 8-1
Lahendus
JUHTMÕTTED (1) Me ei saa kasutada töö arvutamiseks valemit 7-12 (). See pole võimalik sellepärast, et nurk gravitatsioonijõu ja nihkevektori vahel muutub juustutüki liikumisel meile mitte teadaoleval viisil. (Isegi siis, kui me teaksime liikumistee kuju ja oskaksime leida nurka , võiks töö arvutamine olla üsna keeruline.) (2) Kuna aga on konservatiivne jõud, võime me töö arvutamiseks valida mingi teise tee punktide ja vahel – sellise, mis muudab arvutamise lihtsaks.
Arvutused: Valime teekonnaks joonisel 8-5b kujutatud kriipsjoone, mis koosneb kahest sirglõigust. Liikumisel piki horisontaalset lõiku on nurk konstantne, võrdudes . Ja ehkki me ei tea, milline on nihe piki horisontaalset lõiku, ütleb valem 7-12, et sellel lõigul tehtav töö on
Vertikaalse lõigu kohta me teame, et nihke suurus on , ja kuna nii kui on suunatud allapoole, on nende vaheline nurk konstantselt null. Valemi 7-12 abil saame nüüd arvutada kriipsjoone vertikaalsel lõigul tehtava töö :
Kogu töö, mida teeb juustutükile mõjuv jõud selle liikumisel punktist punkti piki kriipsjoont, on seega
Sama suur on ka töö, mis tehakse juustu liikumisel punktist punkti piki pideva joonega kõverat.
Järgnevalt leiame valemid, mis võimaldavad arvutada potentsiaalse energia suurust selles peatükis käsitletud kahe potentsiaalse energia tüübi korral: gravitatsiooni potentsiaalne energia ning deformatsiooni potentsiaalne energia. Aga enne seda tuleb leida üldisem seos konservatiivse jõu ja sellega seotud potentsiaalse energia vahel.
Vaatleme punktmassina käsitletavat keha, mis kuulub süsteemi, kus toimib konservatiivne jõud . Kui see jõud teeb keha liikumisel töö , on süsteemi potentsiaalse energia muutus võrdne ja vastasmärgiline tehtud tööga. See fakt on meil kirjas valemina 8-1 (). Kõige üldisemal juhul, kui see jõud sõltub keha asukohast, saab tööd W arvutada valemiga 7-32:
Selle valemi abil leiame töö, mida teeb jõud keha liikumisel punktist punkti , mistõttu muutub süsteemi olek. (Kuna jõud on konservatiivne, on tehtud töö ühesugune kõigi neid kahte punkti ühendavate teede jaoks.)
Pannes valemi 8-5 valemisse 8-1, saame süsteemi oleku muutusele vastava potentsiaalse energia muutuse üldvalemi:
Vaatleme punktmassi massiga , mis liigub vertikaalselt üles piki -telge (positiivse suunaga üles). Kui punktmass liigub punktist punkti , teeb temale mõjuv gravitatsioonijõud tööd. Et leida sellest tulenevat süsteemi punktmass–Maa potentsiaalse energia muutust, kasutame valemit 8-6, aga kahe erinevusega. (1) Me integreerime -telje asemel piki -telge, kuna gravitatsioonijõud mõjub püstsuunas. (2) Me paneme jõudu tähistava sümboli asemele , kuna just väljendab gravitatsioonijõu suurust, jõud aga on suunatud piki -telge allapoole. Nii saame
mis annab tulemuseks
Füüsikalist mõtet omab ainult gravitatsiooni potentsiaalse energia (ja üldse igasuguse potentsiaalse energia) muut . Et lihtsustada arvutusi või arutelu, võime omistada teatud kindla potentsiaalse energia väärtuse süsteemi punktmass–Maa ühele kindlale olekule, kus punktmass on kõrgusel . Sellisel juhul saab valemi 8-7 kirjutada kujul
Edaspidi nimetame potentsiaalset energiat süsteemi potentsiaalseks energiaks tugiolekus, kus punktmass asub tugipunktis . Tavaliselt võetakse ja , misjärel valem 8-8 saab kuju
See valem ütleb, et
Järgnevalt võtame vaatluse alla joonisel 8-3 kujutatud klotsist ja vedrust moodustatud süsteemi, kus klotsiga koos liigub vedru ots ning vedru elastsustegur on . Kui klots liigub punktist punkti , teeb temale mõjuv vedru elastsusjõud tööd. Et leida süsteemi klots–vedru potentsiaalse energia muutust, paneme valemis 8-6 asemele . Nii saame
ehk
Et siduda potentsiaalset energiat klotsi asukohaga , valime süsteemi tugioleku nii, et vedru on seal vabas olekus ja klots asub punktis . Sel juhul on elastsuse potentsiaalne energia ja valem 8-10 saab kuju
mis annab
KONTROLLKÜSIMUS 2
Juhis 1: Mõiste „potentsiaalne energia” kasutamine.
Potentsiaalne energia on seotud süsteemi kui tervikuga. Sellegipoolest näeme, et paljudel juhtudel seostub see süsteemi mingi osa olekuga, nagu näiteks lauses: „Puu otsas rippuva õuna potentsiaalne energia on .” Selline lähenemine on lubatav, kuid tuleb meeles pidada, et tegelikult on see potentsiaalne energia seotud süsteemiga – antud juhul õunast ja Maast koosneva süsteemiga. Veel tuleb meeles pidada, et kui kehale või süsteemile on omistatud potentsiaalse energia kindel väärtus nagu eespool toodud , on sel mõtet üksnes juhul, kui on teada süsteemi potentsiaalne energia tugiolekus, nagu demonstreerime järgnevas näidisülesandes 8-2.
Laiskloom massiga ripub maapinnast kõrgusel (joonis 8-6).
(a)
Lahendus
JUHTMÕTE Pärast tugipunkti valimist saame valemi 8-9 abil arvutada gravitatsiooni potentsiaalse energia selle tugipunkti suhtes.
(b)
Lahendus
JUHTMÕTE Potentsiaalse energia muutus ei sõltu tugipunkti valikust, kuid ta sõltub kõrguse muutusest .
Arvutused: Kõigil neljal juhul on kõrguse muutus . Järelikult annab valem 8-7 kõigi juhtude jaoks
Süsteemi mehaaniline energia on tema potentsiaalse energia ja temasse kuuluvate kehade kineetilise energia summa.
Käesolevas paragrahvis uurime, mis juhtub mehaanilise energiaga süsteemis, kus energia ülekandumine toimub üksnes konservatiivsete jõudude abil – see tähendab, et selle süsteemi kehadele ei mõju ei hõõrde- ega takistusjõud. Veel oletame, et süsteem on ülejäänud keskkonnast isoleeritud; see tähendab, et süsteemi energia muutumist ei tekita ükski välisjõud (süsteemist väljapoole jäävate kehade toime).
Kui sellisesse süsteemi kuuluvale kehale mõjuv konservatiivne jõud teeb töö , tähendab see energia muundumist keha kineetilisest energiast süsteemi potentsiaalseks energiaks või vastupidi. Valemist 7-10 teame, et kineetilise energia muutus on
ja valemist 8-1 saame potentsiaalse energia muutuse :
Ühendades valemid 8-13 ja 8-14, saame
mis tähendab, et üks energiatest kasvab täpselt nii palju, kui teine kahaneb.
Kui valem 8-15 lahti kirjutada, saame
kus indeksid tähistavad kaht eri ajahetke ja seega süsteemi kehade kaht erinevat paigutust. Valemi 8-16 liikmete ümberpaigutamine annab
Sõnades väljendatuna
juhul, kui süsteem on isoleeritud ja selle kehade vahel toimivad üksnes konservatiivsed jõud. Teiste sõnadega:
Seda väidet nimetatakse mehaanilise energia jäävuse seaduseks (inglise keeles law of conservation; siit on tulnudki nimetus konservatiivsed jõud). Valemi 8-15 abil saame sellele seadusele anda veel ühe kuju:
Mehaanilise energia jäävuse seaduse abiga saame lahendada ülesandeid, mille lahendamine ainult Newtoni seaduste abil oleks üsnagi keeruline:
Kui süsteemi mehaaniline energia on jääv, võime kineetilise ja potentsiaalse energia summa väärtuse ühel ajahetkel omistada ka suvalisele teisele hetkele, arvestamata vahepealseid liikumisi ja arvutamata süsteemis mõjuvate jõudude poolt tehtud tööd.
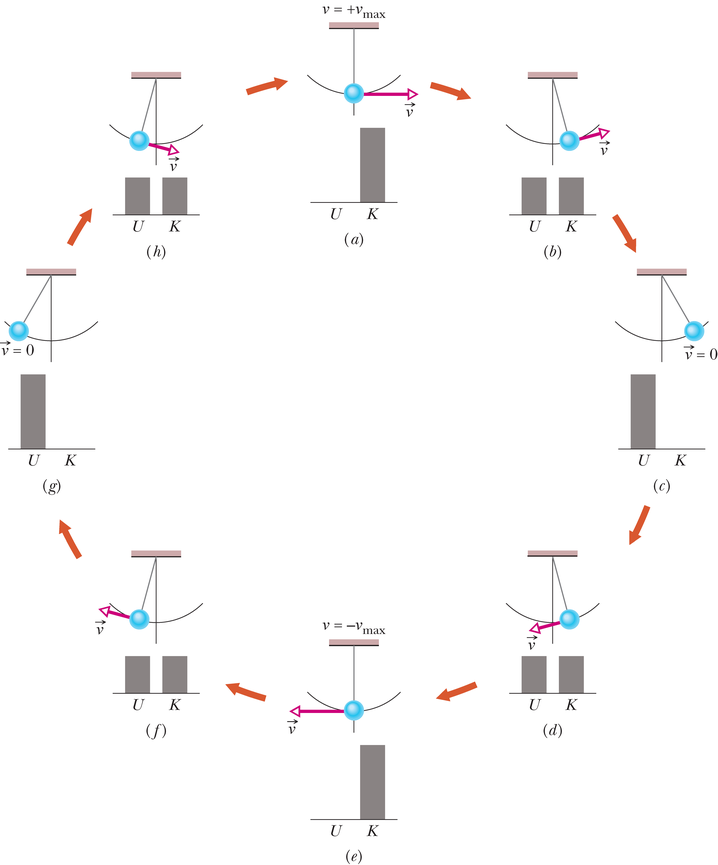
Joonisel 8-7 näete, kuidas rakendatakse mehaanilise energia jäävuse seadust: pendli võnkumise käigus muutub süsteemi pendel–Maa energia kineetilise energia ning gravitatsiooni potentsiaalse energia vahel edasi-tagasi, kusjuures summa jääb kogu aeg konstantseks. Kui me teame gravitatsioonilist potentsiaalset energiat hetkel, kui pendli kuul on oma kõrgeimas asendis (joonis 8-7c), annab valem 8-17 meile kuuli kineetilise energia hetkel, kui see asub madalaimas asendis (joonis 8-7e).
Valime tugipunktiks näiteks pendlikuuli madalaima asendi, võttes seal gravitatsiooni potentsiaalseks energiaks . Oletame, et kuuli kõrgeima asendi korral on gravitatsiooni potentsiaalne energia tugipunkti suhtes . Kuna kuul kõrgeimasse asendisse jõudmisel hetkeks peatub, on tema kineetiline energia seal . Kui panna need arvud valemisse 8-17, saame kuuli kineetilise energia alumises asendis,
Märgime, et selle tulemuse saamiseks ei uurinud me kuuli liikumist ülemisest asendist alumisse ega arvutanud selle liikumise käigus kuulile mõjunud jõudude tööd.
KONTROLLKÜSIMUS 3
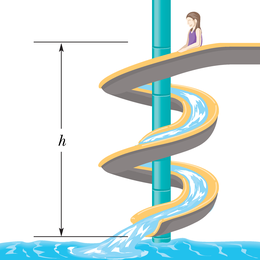
Näidisülesanne 8-3 Arenda oma oskusi
Lahendus
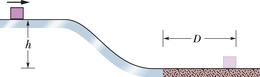
JUHTMÕTTED (1) Me ei saa arvutada lapse kiirust liutoru lõpus kiirenduse järgi, nagu me tegime seda eelmistes peatükkides, sest me ei tea liumäe kaldenurka. Kuna aga see kiirus on seotud lapse kineetilise energiaga, võime kiiruse leidmisel kasutada mehaanilise energia jäävuse seadust. Sel juhul ei ole meil tarvis kaldenurka teada. (2) Mehaaniline energia on jääv siis, kui süsteem on isoleeritud ja kui energia ülekandumine toimub ainult konservatiivsete jõudude kaudu. Kontrollime seda.
Jõud: Lapsele mõjub kaks jõudu. Gravitatsioonijõud, mis teeb tööd tema liikumisel, on konservatiivne jõud. Kaldpinna normaaljõud ei tee tööd selle pärast, et on laskumise igas punktis risti lapse liikumissuunaga.
Süsteem: Kuna lapsele mõjuvatest jõududest teeb tööd ainult gravitatsioonijõud, valime oma süsteemiks süsteemi laps–Maa, mille võime lugeda isoleerituks.
Järelikult on meil tegemist isoleeritud süsteemiga, kus tööd teevad ainult konservatiivsed jõud; seega me tohime siin kasutada mehaanilise energia jäävuse seadust.
Arvutused: Tähistame mehaanilise koguenergia hetkel, kus laps asub liutoru ülemises punktis, ja kui ta asub liutoru alumises otsas. Jäävusseadus ütleb, et
Et näidata mehaanilise energia mõlemat liiki, kirjutame:
ehk
Jagades mõlemaid pooli massiga m ning teisendades saadud avaldist, saame
See on võrdne kiirusega, mille saaks laps kukkudes vertikaalsihis võrra. Reaalsetes liutorudes mõjub alati ka mingi hõõrdejõud, mistõttu lapse kiirus on väiksem.
Kommentaar: Kuigi seda ülesannet saab lahendada otseselt Newtoni seadusi kasutades, on see keeruline ja mehaanilise energia jäävuse seaduse rakendamine muudab selle palju lihtsamaks. Kui meilt aga küsitakse aega, mis kulub lapsel piki liutoru ülalt alla jõudmiseks, siis energiaga seotud meetodid meid ei aita; me peame ikkagi teadma liutoru kuju ja lahendama üsnagi keeruka ülesande.
Juhis 2: Mehaanilise energia jäävuse seadus.
Mehaanilise energia jäävuse seaduse kasutamist ülesannete lahendamisel alustage järgmistele küsimustele vastamisest.
Millistes süsteemides on mehaaniline energia jääv? Te peate suutma eristada oma süsteemi ümbritsevast. Kujutage ette kinnist pinda, mille sisse jäävad kehad kuuluvad teie süsteemi ja sellest välja jäävad kuuluvad ümbrusesse.
Kas hõõrdumis- ja takistusjõud on olemas? Kui jah, siis mehaaniline energia ei ole jääv.
Kas teie süsteem on isoleeritud? Mehaanilise energia jäävuse seadus kehtib ainult isoleeritud süsteemides. See tähendab, et ükski välisjõud (jõud, mis mõjub süsteemi kuuluvate ja süsteemi mittekuuluvate kehade vahel) ei tohi teha tööd süsteemi oleku muutumisel (sinna kuuluvate kehade liikumisel).
Milline on teie süsteemi alg- ja lõpp-olek? Süsteemi kehade paiknemine muutub liikumise käigus. Mehaanilise energia jäävuse seaduse rakendamine tähendab, et väärtus on ühesugune mõlemas olekus. Te peate teadma, mida need olekud endast kujutavad.
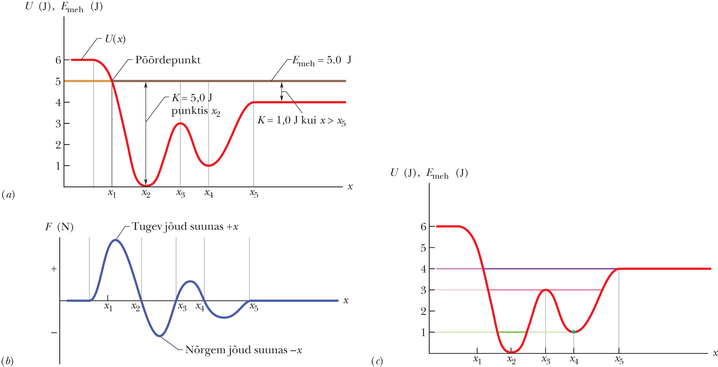
Vaatleme jällegi punktmassi, mis on osa sellisest süsteemist, kus toimivad üksnes konservatiivsed jõud. Seekord oletame, et ajal, kui need jõud teevad tööd, liigub punktmass piki -telge. Me võime punktmassi liikumise kohta paljugi teada saada, kui uurime potentsiaalse energia graafikut. Enne graafikute juurde asumist peame siiski teadma veel üht sõltuvust.
Valem 8-6 näitab, kuidas saab leida kahe punkti vahelist potentsiaalse energia muutust ühemõõtmelises ülesandes juhul, kui on teada jõud . Nüüd teeme teistpidi: katsume leida jõudu, kui teada on potentsiaalse energia sõltuvus asukohast .
Ühemõõtmelise liikumise korral avaldub punktmassile mõjuva jõu töö punktmassi nihkel kui . Valemi 8-1 saame kirjutada kujul
Avaldades siit ja minnes üle piirväärtusele, saame
mis ongi otsitud sõltuvus.
Et tulemust kontrollida, paneme saadud valemisse vedru elastsuse potentsiaalse energia avaldise . Valem 8-22 annab nüüd jõu ehk Hooke’i seaduse, mida oligi oodata. Niisamuti võime valemisse panna süsteemi punktmass–Maa gravitatsiooni potentsiaalse energia avaldise , kus on punktmassi mass ja tema kõrgus maapinna suhtes. Valemist 8-22 saame sel juhul , mis ongi punktmassile mõjuv gravitatsioonijõud.
Joonisel 8-9a on esitatud potentsiaalse energia graafik sellise süsteemi jaoks, kus punktmassi ühemõõtmelise liikumise käigus tehtava töö põhjustab konservatiivne jõud . Jõudu on lihtne leida graafiliselt, mõõtes kõvera tõusu selle erinevates punktides. (Valem 8-22 järgi on jõud võrdne ja vastasmärgiline kõvera tõusuga.) Joonisel 8-9b on esitatud jõu sellisel viisil leitud graafik.
Kui mittekonservatiivsed jõud puuduvad, on süsteemi mehaanilisel energial konstantne väärtus, mis on antud valemiga
on siin süsteemi kuuluva punktmassi kineetilist energiat kirjeldav funktsioon ( tähendab, et kineetiline energia sõltub punktmassi asukohast ). Valemi 8-23 võime kirjutada kujul
Oletame, et (peame meeles, et see suurus on konstantne) on juhtumisi . Joonisel 8-9a kujutab seda horisontaalne joon, mis jõuab energia teljeni punktis . Valem 8-24 ütleb, kuidas määrata kineetilist energiat punktmassi mistahes asukoha korral: leiame graafikult asukohale vastava väärtuse ning lahutame selle mehaanilisest koguenergiast . Näiteks kui punktmassi asukoht jääb -st paremale, siis . Suurim väärtus () vastab punktmassi asukohale x2 ja vähim () asukohale x1.
Kuna ei saa kunagi olla negatiivne (sest v2 on alati positiivne), siis ei saa punktmass kunagi minna vasakule punktist x1, kuna seal on negatiivne. Selle asemel väheneb punktmassi kineetiline energia tema liikumisel punktist x2 punkti x1 poole (liikumine aeglustub), kuni punktis x1 on (punktmass peatub selles punktis).
Märgime, et punktmassi jõudmisel punkti x1 on temale mõjuv jõud valemi 8-22 kohaselt positiivne (kuna kõvera tõus on negatiivne). See tähendab, et punktmass ei jää punktis x1 seisma, vaid alustab liikumist paremale, varasemale liikumisele vastassuunas. Järelikult on x1 pöördepunkt, kus (kuna ) ja punktmass muudab liikumissuunda. Et graafiku parempoolses osas pöördepunkte ei ole, siis sinnapoole liikumine kestab lõpmatult.
Joonisel 8-9c on toodud potentsiaalse energia kõver jooniselt 8-9a, millele on kantud kolm eri väärtust. Kui (lilla joon), nihkub pöördepunkt punktist x1 punktide x1 ja x2 vahele. Kõigis punktides, mis jäävad punktist paremale poole, on süsteemi mehaaniline energia võrdne potentsiaalse energiaga; seetõttu on tema kineetiline energia null ja kuna (valemi 8-22 kohaselt) talle ei mõju ka ükski jõud, peab ta seal olema paigal. Punktmassi sellist seisundit nimetatakse neutraalseks ehk ükskõikseks tasakaaluks. (Sellises seisundis on horisontaalsele lauale asetatud piljardimuna.)
Kui (roosa joon), siis on meil kaks pöördepunkti: üks punktide x1 ja x2, teine punktide ja vahel. Neile lisandub veel punkt , kus . Kui punktmass asub täpselt selles punktis, on temale mõjuv jõud samuti null ja ta jääb seal paigale. Kui teda aga nihutada ükskõik kui vähe ükskõik kummas suunas, lükkab nullist erinev jõud teda nihkega samas suunas ja punktmass jätkab liikumist. Punktmassi sellist asendit nimetatakse ebapüsivaks (ebastabiilseks ehk labiilseks) tasakaaluks. (Näitena võib tuua piljardimuna, mis on asetatud keeglikuuli peale.)
Järgmisena vaatleme punktmassi käitumist juhul, kui (roheline joon). Kui paneme ta punkti , jääb ta sinna. Ta ei saa liikuda ei vasakule ega paremale, kuna mõlemal juhul tooks see kaasa negatiivse kineetilise energia. Kui teda tõugata vasakule või paremale, ilmneb taastav jõud, mis viib punktmassi tagasi punkti . Punktmassi sellist seisundit nimetatakse püsivaks (stabiilseks) tasakaaluks. (Näitena võib tuua poolsfääri kujulise kausi põhjas oleva piljardimuna.) Kui punktmass asub kausikujulises potentsiaaliaugus keskmega punktis x2, kahe pöördepunkti vahel, saab ta küll mingil määral liikuda, aga ainult jupikese teest x1 või poole.
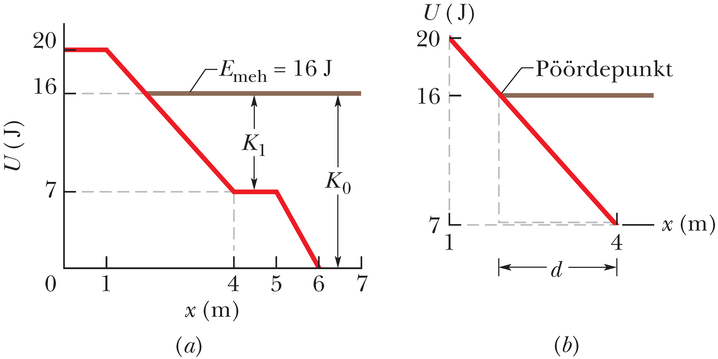
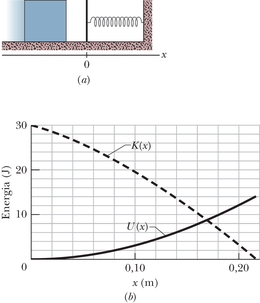
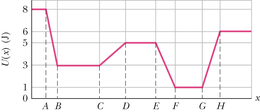
Punktmass massiga liigub ühemõõtmeliselt piki -telge, kus talle mõjub sama telje sihiline konservatiivne jõud. Joonisel 8-10a on kujutatud selle jõuga seotud potentsiaalse energia sõltuvus asukohast . See tähendab, et kui punktmass asub ükskõik kus punktide ja vahel, siis on tal graafikule vastav potentsiaalne energia . Punktis on punktmassi kiirus .
(a)
Lahendus
JUHTMÕTTED (1) Punktmassi kineetiline energia on määratud valemiga 7-1 (). (2) Kuna punktmassile mõjuvad üksnes konservatiivsed jõud, on tema mehaaniline energia () jääv kogu liikumise vältel. (3) Järelikult, kui meil on olemas selline graafik nagu joonisel 8-10a, peab kineetiline energia olema võrdne mehaanilise koguenergia ja potentsiaalse energia vahega.
Arvutused: Punktis on punktmassi kineetiline energia
Kuna selles punktis on potentsiaalne energia , siis on mehaaniline koguenergia
Seda väärtust kujutab joonisel 8-10a pruun horisontaalne joon. Näeme, et punktis on potentsiaalse energia väärtuseks . Kineetiline energia on võrdne ja vahega:
(b)
Lahendus
JUHTMÕTE Pöördepunkt on koht, kus punktmassile mõjuv jõud ta hetkeks peatab, et sundida teda seejärel liikuma vastassuunas. See koht asub seal, kus punktmassi hetkkiirus on ja järelikult .
Arvutused: Kuivõrd väljendab ja erinevust, tuleb meil joonisel 8-10a leida koht, kus kasvav kohtub tähistava horisontaalse joonega, nagu on näidatud joonisel 8-10b.
Kuna ka graafikuks on sirge, saame joonestada kaks osaliselt kattuvat täisnurkset kolmnurka ja nendest avaldada külgede suhted
mis annab . Seega on pöördepunkti asukoht
(c)
Lahendus
JUHTMÕTE Jõu saab leida valemiga 8-22 (). See ütleb, et ta on võrdne ja vastasmärgiline graafiku tõusuga.
Arvutused: Jooniselt 8-10b näeme, et vahemikus on jõu väärtus
Niisiis on jõu suurus ja ta mõjub -telje positiivses suunas. Tulemus on kooskõlas faktiga, et selle jõu mõjul algselt vasakule poole liikunud punktmass peatub ning hakkab seejärel liikuma paremale.
Eelmises, 7. peatükis defineerisime töö kui kehalt energia äraviimise või juurde toomise temale mõjuva jõu toimel. Laiendame seda definitsiooni kehade süsteemile ja lisame süsteemi kehadele mõjuva välisjõu.
Joonis 8-11a kujutab positiivset tööd (süsteem saab energiat juurde) ja joonis 8-11b negatiivset tööd (süsteemist viiakse energiat ära). Kui süsteemile mõjub rohkem kui üks välisjõud, võrdub juurde toodud või ära viidud energia hulk nende jõudude kogutööga.
Ka need üleviimised sarnanevad raha pangaarvele või sealt ära kandmisele. Kui süsteem koosneb vaid ühestainsast punktmassist või punktmassina käsitletavast kehast, nagu vaatlesime 7. peatükis, saab süsteemile mõjuva jõu töö muuta üksnes selle keha kineetilist energiat. Sellise energia ülekandmise väljenduseks on teoreem tööst ja kineetilisest energiast, valem 7-10 (). See tähendab, et üksikul kehal on vaid üksainus energia-arve, mida nimetatakse kineetiliseks energiaks. Välisjõud võivad sellele arvele energiat juurde tuua või ära viia. Kui süsteem on keerulisem, võivad välisjõud muuta ka teisi energialiike (nagu seda on potentsiaalne energia) – see tähendab, et selline keerukam süsteem võib omada mitmeid energia-arveid.
Püüame nüüd leida energia avaldisi selliste süsteemide tarbeks. Vaatleme kaht põhiolukorda: üht, kus esineb hõõrdumine, ja teist, kus see puudub.
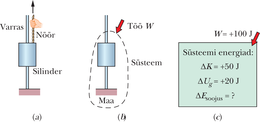
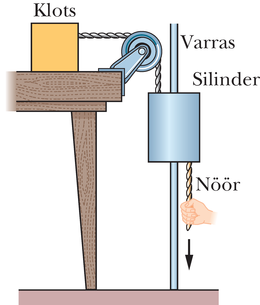
Keeglimängu viskeks valmistudes te kükitate, haarate keeglikuuli alt ning püsti tõustes tõukate kuuli kätega üles, tõstes ta umbes näo kõrgusele. Ülespoole liikumise ajal teeb teie poolt kuulile rakendatud jõud tööd, selle käigus kantakse üle energiat, aga millisele süsteemile?
Enne kui vastata, kontrollime, milline energia muutus. Üks muutusi on kineetilise energia muutus ; aga kuna tõste käigus liikus kuul Maast kaugemale, pidi muutuma ka süsteemi kuul–Maa potentsiaalne energia. Seetõttu on teie poolt rakendatud välisjõu töö süsteemi suhtes
ehk
kus on süsteemi mehaanilise energia muutus. Need kaks valemit, mida illustreerib joonis 8-12, väljendavad samaväärselt süsteemile mõjuva välisjõu poolt tehtavat tööd hõõrdumise puudumisel.
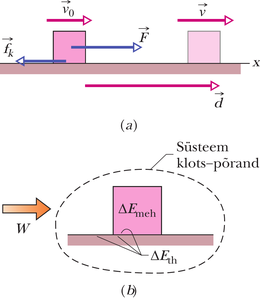
Järgnevalt vaatleme joonisel 8-13a toodud näidet. Konstantne horisontaalne jõud tõmbab klotsi piki -telge nihke võrra, suurendades klotsi kiirust -st kuni -ni. Liikumise ajal mõjub klotsile põranda poolt konstantne hõõrdejõud . Esialgu valime vaadeldavaks süsteemiks klotsi ja rakendame temale Newtoni teist seadust. Paneme kirja selle seaduse -telje suunalise komponendi jaoks ():
Kuna mõlemad jõud on konstantsed, on ka kiirendus konstantne. See lubab kasutada valemit 2-16, saades
Avaldades saadud valemist ja pannes selle valemisse 8-27, saame pärast teisendusi
Üldisemal juhul (näiteks kui klotsi tõmmatakse piki kaldpinda üles) muutub ka potentsiaalne energia. Lisades selle võimaliku muutuse valemisse 8-29, saame
Katse käigus märkame, et nii klots kui ka põranda see osa, mida mööda klots libiseb, soojenevad liikumise käigus. Nagu näeme 18. peatükis, on keha temperatuur seotud tema soojusenergiaga (see on energia, mis seostub kehas olevate aatomite ja molekulide juhuslike liikumistega). Siin suureneb klotsi ja sellega kokku puutuva põranda soojusenergia, kuna (1) nende vahel on hõõrdumine ja (2) on olemas liikumine. Meenutame, et hõõrdumine tekib kahe pinna vahelise külmkeevituse tagajärjel. Kui klots liigub piki põrandat, siis selle liikumise käigus purunevad ja taastuvad need keevitusekohad ning see muudabki pinnad soojemaks. Järelikult suurendab libisemine nende soojusenergiat .
Katsest leiame, et soojusenergia juurdekasv on võrdne ja korrutisega:
Seega võime valemi 8-30 kirjutada kujul
ongi töö , mida teeb väline jõud (ja on selle jõu poolt üle kantud energia), kuid missugune on see süsteem, kus töö tehti (ehk kus toimus energia ülekandumine)? Et leida vastust, tuleb leida, missugused energiad muutusid. Muutusid nii klotsi mehaaniline energia kui ka klotsi ja põranda soojusenergia. Järelikult tegi jõud tööd süsteemi klots-põrand kallal. See töö on
See valem, mida illustreerib joonis 8-13b, väljendabki süsteemi energiabilanssi juhul, kui tööd teeb väline jõud ning kui hõõrdumine on arvesse võetud.
KONTROLLKÜSIMUS 5
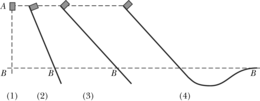
Lihavõttesaare muistsed elanikud valmistasid kivimurrus sadu hiigelkujusid ning paigutasid need eri kohtadesse üle kogu saare (joonis 8-14). Palju on vaieldud selle üle, kuidas neil õnnestus vedada kujusid rohkem kui kaugusele ilma masinate abita. Tõenäoliselt asetati kuju puust kelgule ning veeti seda piki ühesugustest rullikutena töötavatest palkidest rada. Selle meetodi kaasaegse rekonstruktsiooni ajal suutsid meest vedada Lihavõttesaare kuju sarnast eset massiga piki tasast maad minutiga meetri kaugusele.
(a)
Lahendus
JUHTMÕTTED (1) Tehtud töö arvutamiseks saab kasutada valemit 7-7 (W=Fdcosϕ). (2) Et määratleda süsteemi, mille kallal töö tehti, tuleb vaadata, mille energia on muutunud.
Arvutused: Me teame, et valemis 7-7 kaugus on , on mehe poolt kujule rakendatud summaarse jõu suurus ja . Oletame, et iga mees tõmbab jõuga, mis on võrdne mehe kahekordse kaaluga, mis on kõigi jaoks ühesuguselt . Järelikult on meeste summaarne tõmbejõud . Võttes ühe mehe massiks , saame valemist 7-7
Kuna kuju liikus, pidi selle käigus kindlasti toimuma tema kineetilise energia muutus . Võime ka olla kindlad, et kelgu, palkide ja maapinna vahel toimis küllalt suur liikumishõõre, mille tulemuseks oli nende soojusenergia muutus . Järelikult koosnes süsteem, mille kallal töö tehti, kujust, palkidest, kelgust ja maapinnast.
(b)
Lahendus
JUHTMÕTE Me võime seostada jõu poolt tehtava tööga , kasutades energiabilansi valemit 8-33 süsteemi jaoks, kus on olemas hõõrdumine.
Arvutused: Me teame väärtust ülesande eelmisest osast (a). Kuju mehaanilise energia muutus oli null, kuna kuju oli paigal nii enne kui pärast nihutamist ja tema kõrgus maapinna suhtes ei muutunud. Seega saame
(c)
Lahendus
Arvutused: Töö arvutame nagu osas (a), võttes väärtuseks . Võttes jällegi ja võrdseks, saame
Energiakogus, mida kulutasid mehed kuju transportimisel, on üllatavalt suur. Sellele vaatamata võisid meest viia kuju kaugusele ilma salapäraseid energiaallikaid kasutamata.
Transporditööline veab puukasti kapsapeadega (kogumassiga ) piki betoonpõrandat, rakendades konstantset horisontaalset jõudu suurusega . Sirgjoonelise nihke 0,5m jooksul kahanes kasti kiirus esialgselt kuni .
(a)
Lahendus
JUHTMÕTE Kuna rakendatud jõud on konstantne, võime arvutada selle tehtud töö, kasutades valemit 7-7 (W=Fdcosϕ).
Arvutused: Pannes valemisse antud suurused ja arvestades, et jõud ja nihe on samasuunalised, saame
Mõttekäik: Me saame määratleda süsteemi, milles tehti töö, kui vaatame, mille energia muutub. Kuna kasti kiirus muutub, siis muutub kindlasti ka tema kineetiline energia. Aga kas on olemas ka hõõrdumine kasti ja põranda vahel, mis tooks kaasa soojusenergia muutumise? Juhime tähelepanu sellele, et jõu suund ühtib kasti liikumissuunaga. Järelikult kui ei oleks hõõrdumist, peaks kasti kiirus suurenema. Kuna aga kasti liikumine aeglustub, peab olema ka hõõrdumine ning koos sellega kasti ja põranda soojusenergia muutus . Järelikult on süsteemiks, mille kallal tööd tehti, süsteem kast–põrand, kuna selles toimusid mõlemad energiamuutused.
(b)
Lahendus
JUHTMÕTE Me seome jõu poolt tehtud tööga energiabilansi valemi 8-33 abil, mis kehtib hõõrdumisega süsteemide kohta:
Arvutused: Meile on punktist (a) teada töö väärtus. Kasti mehaanilise energia muutus võrdub tema kineetilise energia muutusega, kuna potentsiaalne energia ei muutunud. Järelikult
Pannes selle valemisse 8-34 ning lahendades selle suhtes, saame:
Oleme nüüd vaadanud erinevaid olukordi, kus energiat kantakse üle süsteemidelt ja süsteemidele üsna sarnaselt raha ülekandmisele pangaarvete vahel. Kõigis neis olukordades oleme eeldanud, et sissetoodud energia saab alati ka arvele võetud, see tähendab, et energia ei saa imekombel kaduda või välja ilmuda. Kui öelda seda ametlikumas keeles, siis me eeldasime (õigesti), et energia allub seadusele, mida nimetatakse energia jäävuse seaduseks ja mis kehtib süsteemi koguenergia kohta. Koguenergia saadakse süsteemi mehaanilise energia, soojusenergia ja viimasest erinevate siseenergia liikide summeerimisel. (Seni pole me neid teisi siseenergia liike veel käsitlenud.) See seadus ütleb, et
Ainus energia ülekandmise tüüp, mida oleme vaadelnud, on süsteemiga tehtud töö. Selle nurga all vaadatuna tähendab see seadus, et
kus on süsteemi mehaanilise energia suvaline muutus, on süsteemi soojusenergia suvaline muutus ja on süsteemi siseenergia ükskõik mis muud tüüpi muutus. Mehaanilise energia muutus sisaldab kineetilise energia muutust ning potentsiaalse energia muutust (mis võib olla tingitud gravitatsioonist, elastsusest või millestki muust, mida me võiks leida).
Energia jäävuse seadus ei ole midagi sellist, mida saaks tuletada füüsika alusprintsiipidest. Selle seaduse aluseks on loendamatu hulk katseid. Ei teadlased ega insenerid ole kunagi leidnud ühtki erandit selle seaduse kehtimise kohta.
Kui süsteem on ümbruskonnast isoleeritud, ei saa toimuda energia ülekandumist temasse või temast välja. Sel juhul kõlab energia jäävuse seadus nii:
Süsteemi sees võib samal ajal toimuda mitmeid energia ülekandumisi – näiteks kineetilise ja potentsiaalse või siis kineetilise ja soojusenergia vahel. Selle juures ei saa kõigi energialiikide kogusumma antud süsteemi jaoks muutuda.
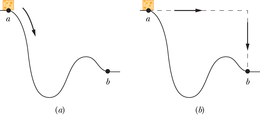
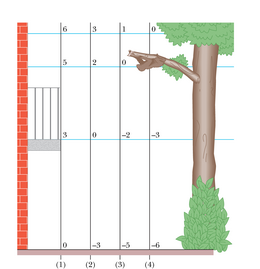
Me võime näitena tuua joonisel 8-8 kujutatud kaljuronija, vaadeldes teda, tema varustust ja Maad kui isoleeritud süsteemi. Kaljult laskumise ajal muudab ta süsteemi olekut ning peab suunama selle süsteemi gravitatsioonilise potentsiaalse energia muutumist. (See energia ei saa niisama kuhugi kaduda.) Osa sellest muutub tema enda kineetiliseks energiaks. Ilmselt ei soovi ta, et see osa oleks liig suur, kuna vastasel juhul hakkaks ta liikuma liiga kiiresti. Nii on ta sidunud köie ümber metallrõngaste, et suurendada laskumise ajal hõõrdumist. Kui köis libiseb läbi rõngaste, muudetakse süsteemis olev gravitatsiooni potentsiaalne energia rõngaste ja köie soojusenergiaks nii, et kaljuronija saaks seda protsessi ohjata. Süsteemi ronija–kandurid–Maa koguenergia (gravitatsiooni potentsiaalne energia, kineetiline ja soojusenergia koos võetuna) ent ei saa laskumise käigus muutuda.
Energia jäävuse seadust saab isoleeritud süsteemide jaoks kirja panna kahel viisil. Esiteks, võttes valemis 8-35 , saame
Aga me võime ka võtta , kus indeksid ja tähistavad kaht erinevat ajahetke – näiteks enne ja pärast mingi protsessi toimumist. Siis saab valem 8-36 kuju
Valem 8-37 ütleb, et
isoleeritud süsteemi korral saame tema koguenergia väärtuse ühel ajahetkel omistada ka suvalisele teisele hetkele ilma vahepealseid energia muutusi arvestamata.
See seadus võib osutuda heaks abivahendiks niisuguste ülesannete lahendamisel, kus on vaja võrrelda süsteemi erinevaid energialiike enne ja pärast mingi protsessi toimumist.
Punktis 8-5 käsitlesime me isoleeritud süsteemide üht erijuhtu – olukorda, kus süsteemis ei toiminud mittekonservatiivset tüüpi jõud (nagu näiteks liikumishõõre). Sellisel juhul on ja mõlemad nullid ja nii taandub valem 8-37 valemiks 8-18. Teiste sõnadega, süsteemi mehaaniline energia on jääv juhul, kui süsteemis ei mõju mittekonservatiivseid jõudusid.
Välisjõud võib muuta keha kineetilist või potentsiaalset energiat ilma selle keha kallal tööd tegemata – see tähendab, ilma kehale energiat üle kandmata. Selle asemel põhjustab see jõud keha enda energia muundumise ühest liigist teise.
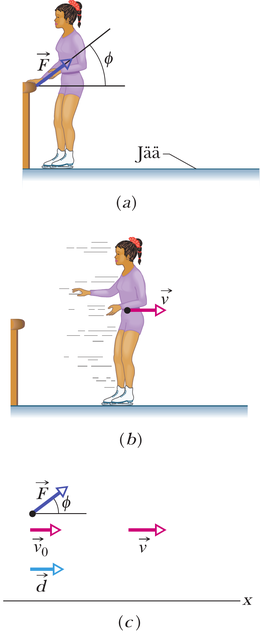
Joonisel 8-16 on toodud üks näide. Paigalseisev uisutaja tõukab end piirdest eemale ja libiseb siis üle jää (joonis 8-16a ja b). Tema kineetiline energia kasvab, kuna piire mõjutab teda välise jõuga . See jõud aga ei vii energiat piirdelt uisutajale. Järelikult see jõud tööd ei tee. Uisutaja kineetiline energia kasvab tema lihaste biokeemilise energia muundamise tagajärjel.
Joonis 8-17 kujutab teist näidet. Töötav mootor suurendab neliveolise auto kiirust (mootor paneb pöörlema kõiki nelja ratast). Kiirendamise käigus sunnib mootor auto rehve tõukama tee pinda tahapoole. See tõukumine tekitab hõõrdejõu , mis mõjub kõigile rehvidele suunaga ettepoole. Auto kineetiline energia kasvab, kuna väline kogujõud , mis on võrdne kõigi nende hõõrdejõudude summaga, kiirendab auto liikumist. See jõud ei kanna aga energiat üle teekattelt autole ja järelikult ei tee ka auto kallal tööd. Auto kineetilise energia suurenemise põhjuseks on hoopis kütuses sisalduva energia sisemine ülekandumine.
Mõnikord nagu eeltoodud näiteis saab lihtsustavate eelduste abil siduda keha mehaanilise energia muutuse talle mõjuva välisjõuga. Vaatame näidet uisutajaga. Barjäärist lahti tõukamise ajal läbitud vahemaa jaoks (joonisel 8-16c) teeme lihtsustava oletuse, et kiirendus oli seal konstantne ja uisutaja kiirus kasvas nullist kuni väärtuseni . (See tähendab ka oletust, et temale mõjuv jõud oli konstantne nii suuruse kui nurga poolest.) Pärast lahtitõuget lihtsustame olukorda sellega, et loeme uisutaja punktmassiks ja jätame arvestamata fakti, et tema lihaste pingutus tõi kaasa nende soojusenergia suurenemise ja muutis ka teisi füsioloogilisi parameetreid. Ainult nii saame rakendada valemit 7-5 () ning kirjutada
ehk
Kui muutub ka keha kõrgus, lisame gravitatsiooni potentsiaalse energia ning kirjutame
Ka siin ei tee võrrandi paremas pooles olev jõud tööd, olles sellegipoolest vajalik vasakus pooles kirja pandud energiamuutuste põhjendamisel.
Nüüd, olles näinud, kuidas toimub energia muundumine ühest liigist teise, võime laiendada ka paragrahvis 7-9 toodud võimsuse mõistet. Seal defineerisime võimsuse kui kiiruse, millega jõud teeb tööd. Märksa üldisema definitsiooni saame öeldes, et võimsus on kiirus, millega jõud muundab energiat ühest liigist teise. Kui aja jooksul viiakse üle energiahulk , siis avaldub üleviimist teostava jõu keskmine võimsus valemiga
Samal kombel saame defineerida hetkvõimsuse
Näidisülesanne 8-7
Lahendus
JUHTMÕTTED Tuleb kontrollida kõiki jõudusid ja seejärel otsustada, kas tegu on isoleeritud süsteemiga või süsteemiga, milles teeb tööd mingi välisjõud.
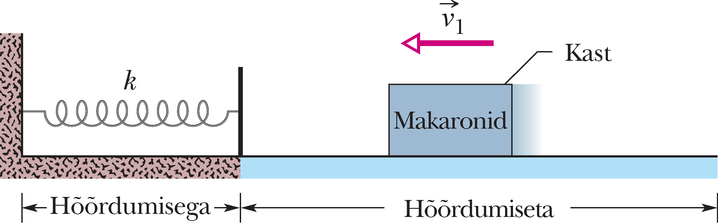
Jõud: Kastile mõjuv normaaljõud tööd ei tee, kuna tema suund on alati risti kasti liikumissuunaga. Samal põhjusel ei tee tööd ka kastile mõjuv gravitatsioonijõud. Kui vedru on kokku surutud, teeb tema elastsusjõud tööd, muundades kasti kineetilist energiat elastsuse potentsiaalseks energiaks. Sama suur elastsusjõud mõjub ka seinale, mis aga jääb liikumatuks. Kasti ja põranda vahel toimiv hõõrdejõud suurendab kasti liikumise ajal nende soojusenergiat.
Süsteem: Süsteem kast–vedru–põrand koondab kõik need jõud ning energia ülekandumised ühte isoleeritud süsteemi. Kuna süsteem on isoleeritud, ei saa tema koguenergia muutuda. Seetõttu võime kasutada energia jäävuse seadust valemi 8-37 kujul:
Arvutused: Valemis 8-42 vastab indeks libiseva kasti algolekule ja indeks olekule, kus kast on hetkeks peatunud ning vedru on kokku surutud pikkuse võrra. Mõlemal juhul koosneb süsteemi mehaaniline energia kasti kineetilise energia () ja vedru potentsiaalse energia () summast. Olekus on (kuna vedru ei ole kokku surutud) ja kasti kiirus on . Siit saame:
Olekus on (kuna kast on peatunud) ja vedru on pikkuse võrra kokku surutud. Saame
Lõpuks lisame valemist 8-31 leitava soojusenergia juurdekasvu , mille leiame kasti ja põranda vahelise hõõrdejõu ja nihke korrutisena . Valem 8-42 annab nüüd
Pannes sellesse teadaolevad andmed ning rühmitades saadud avaldist, saame (SI-s)
Lahendame ruutvõrrandi ja leiame, et
Näidisülesanne 8-8
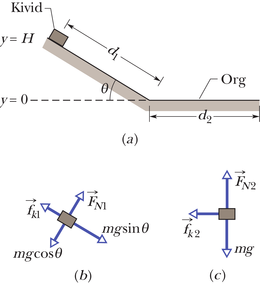
Lahendus
JUHTMÕTTED (1) Süsteemi kivid–Maa mehaaniline energia on kivide kineetilise energia () ja gravitatsiooni potentsiaalse energia () summa. (2) Mehaaniline energia ei ole jääv, kuna kividele mõjuv mittekonservatiivne hõõrdejõud muudab energiahulga kivide ja maapinna soojusenergiaks. (3) Muundatav energia sõltub vastavalt valemile 8-31 () liikumishõõrdejõust ning kivide poolt läbitud tee pikkusest. (4) Laviini tee suvalises punktis sõltub tema järelejäänud mehaaniline energia esialgsest mehaanilisest energiast ja soojusenergiast valemi 8-37 kohaselt ehk antud juhul .
Arvutused: Mehaaniline lõppenergia võrdub mehaaniline algenergia miinus energiakadu , mis muutus soojusenergiaks:
Kuna laskumise alguses oli kivide potentsiaalne energia ja kineetiline energia , on mehaanilise energia algväärtuseks . Lõpus, kui kivid on peatunud, on nende potentsiaalne energia ja kineetiline energia , seega on ka mehaaniline koguenergia . Soojusenergiaks muutunud energiahulk on nõlva pidi laskumisel ja piki orupõhja liikumisel . Pannes need valemisse 8-43, saame
Jooniselt 8-19a näeme, et . Liikumishõõrdejõu arvutamiseks kasutame valemit 6-2 (). Kuuendas peatükis nägime, et kaldpinna normaaljõud nullib gravitatsioonijõu komponendi , mis on pinnaga risti (joonis 8-19b). Viiendast peatükist teame, et horisontaalsel pinnal on normaaljõud võrdne kogu gravitatsioonijõuga (joonis 8-19c). Pannes kõik need avaldised valemisse 8-44 ja avaldades sellest , leiame
ning
Kommentaar: Saadud tulemus on tõepärane väikeste laviinide korral. Suurte puhul võib suhe olla isegi . Kui panna see valemisse 8-45 ja leida siis liikumishõõrdetegur, saame, et . Uurijate jaoks on arusaamatu, kuidas võib tohutu hulk sakilisi uperpallitavaid kive omada hõõrdetegurit, mis oma väiksuse poolest on võrreldav üsna libeda jääga. Üks perspektiivikamaid seletusi ütleb, et laviini massiivsem osa hõljub väikestest üles-alla võnkuvatest osakestest koosneval kihil ega puutugi maapinda enne, kui laviin peatub.
Näidisülesanne 8-9
Lahendus
JUHTMÕTTED (1) Vedru kokkusurumise käigus ei ole süsteemi mehaaniline energia () jääv, kuna klotsile mõjub mittekonservatiivne hõõrdejõud, mis muudab energiahulga klotsi ja põranda soojusenergiaks. (2) Äraviidud energia sõltub hõõrdejõu suurusest ja läbitud tee pikkusest vastavalt valemile 8-31 (). (3) Vedru kokkusurumise ajal on mehaaniline koguenergia klotsi mistahes asukoha jaoks () arvutatav mehaanilisest energiast algasendis () ja soojuseks muudetud energiahulgast () valemiga 8-37 – ehk käesoleval juhul .
Kuidas leida ? Jooniselt 8-20b näeme, et kui klots asub punktis ja vedru pole veel kokku suruma hakatud, on klotsi kineetiline energia ning vedru potentsiaalne energia . Seega on ja summa
Vedru on maksimaalselt kokku surutud hetkel, kui klots peatub – see tähendab, tema kineetiline energia on vähenenud nullini. Graafikult loeme, et see juhtub punktis , kus ja . Seega on peatumispunktis ja summa
Et leida soojuseks muutunud energia hulka, tuleb kirjutada valem :
ja
Kuidas leida ? Valemist 6-2 teame, et liikumishõõrdejõud avaldub , kus normaaljõud leitakse valemiga 5-14 (). Siin muudab hõõrdejõud teepikkusel soojuseks energiahulga . Kui need kaks valemit kokku panna, saame
Asendades siia algandmed , , g=9,8m/s2 ja , leiame, et
Konservatiivsed jõud
Jõud on konservatiivne jõud siis, kui tema kogutöö punktmassi liikumisel piki suletud teekonda lähtepunktist tagasi samasse punkti on null. Samuti võib öelda, et jõud on konservatiivne siis, kui tema töö punktmassi liikumi